4
Integer Factorization
The Integer Factorization Problem (IFP) is one of the most important infeasible problems in computational number theory, for which there is still no polynomial-time algorithm for solving it. In this chapter we discuss several important modern algorithms for factoring, including
- Pollard’s
 and p−1 Methods;
and p−1 Methods; - Lenstra’s Elliptic Curve Method (ECM);
- Pomerance’s Quadratic Sieve (QS), and
- The currently fastest method, Number Field Sieve (NFS).
4.1 Basic Concepts
The Integer Factorization Problem (IFP) may be described as follows:
(4.1) 
Clearly, if there is an algorithm to test whether or not an integer n is a prime, and an algorithm to find a nontrivial factor f of a composite integer n, then by recursively calling the primality testing algorithm and the integer factorization algorithm, it should be easy to find the prime factorization of
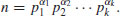
Generally speaking, the most useful factoring algorithms fall into one of the following two main classes:
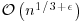 .
.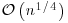 .
.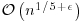 .
.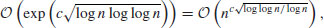
 .
.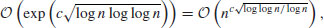
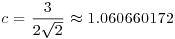 .
.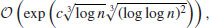
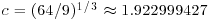 if GNFS (a general version of NFS) is used to factor an arbitrary integer n, whereas
if GNFS (a general version of NFS) is used to factor an arbitrary integer n, whereas 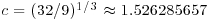 if SNFS (a special version of NFS) is used to factor a special integer n such as
if SNFS (a special version of NFS) is used to factor a special integer n such as 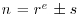 , where r and s are small, r>1 and e is large. This is substantially and asymptotically faster than any other currently known factoring method.
, where r and s are small, r>1 and e is large. This is substantially and asymptotically faster than any other currently known factoring method. .) Examples are:
.) Examples are: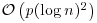 .
.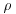 Method (also known as Pollard’s “rho” algorithm), which under plausible assumptions has expected running time
Method (also known as Pollard’s “rho” algorithm), which under plausible assumptions has expected running time 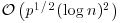 .
.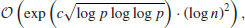
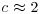 is a constant (depending on the details of the algorithm).
is a constant (depending on the details of the algorithm). is for the cost of performing arithmetic operations on numbers which are
is for the cost of performing arithmetic operations on numbers which are 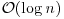 or
or  bits long; the second can be theoretically replaced by
bits long; the second can be theoretically replaced by 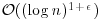 for any
for any 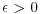 .
.Note that there is a quantum factoring algorithm, first proposed by Shor, which can run in polynomial-time
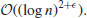
However, this quantum algorithm requires running on a practical quantum computer with several thousand quantum bits, which is not available at present.
In practice, algorithms in both categories are important. It is sometimes very difficult to say whether one method is better than another, but it is generally worth attempting to find small factors with algorithms in the second class before using the algorithms in the first class. That is, we could first try the trial division algorithm, then use some other method such as NFS. This fact shows that the trial division method is still useful for integer factorization, even though it is simple. In this chapter we shall introduce some most the useful and widely used factoring algorithms.
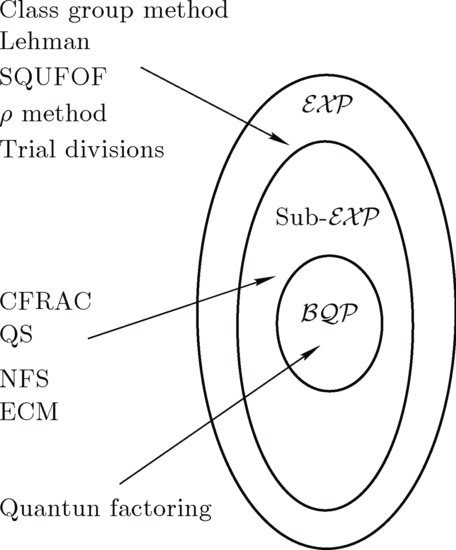
From a computational complexity point of view, the IFP is an infeasible (intractable) problem, since there is no polynomial-time algorithm for solving it; all the existing algorithms for IFP run in subexponential-time or above (see Figure 4.1).
Figure 4.1 Algorithms/Methods for IFP
Problems for Section 4.1
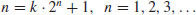
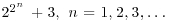 contains infinitely many composites.
contains infinitely many composites.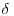 be the number defined by
be the number defined by 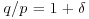 such that
such that 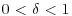 . Show that the number of steps used in the Fermat factoring method is approximately
. Show that the number of steps used in the Fermat factoring method is approximately 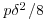 .
.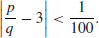
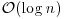 bit operations.
bit operations.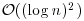 bit operations.
bit operations.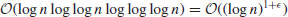
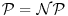 , then
, then 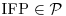 .
.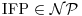 -complete.
-complete.4.2 Trial Divisions Factoring
The simplest factoring algorithm is perhaps the trial division method, which tries all the possible divisors of n to obtain its complete prime factorization:
(4.2) 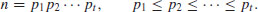
The following is the algorithm:
Algorithm 4.1 (Factoring by trial divisions) This algorithm tries to factor an integer n>1 using trial divisions by all the possible divisors of n.
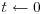 ,
, 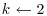 .
.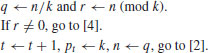
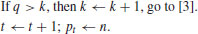
Exercise 4.1 Use Algorithm 4.1 to factor n = 2759.
An immediate improvement of Algorithm 4.1 is to make use of an auxiliary sequence of trial divisors:
(4.3) 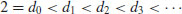
which includes all primes  (possibly some composites as well if it is convenient to do so) and at least one value
(possibly some composites as well if it is convenient to do so) and at least one value 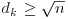 . The algorithm can be described as follows:
. The algorithm can be described as follows:
Algorithm 4.2 (Factoring by Trial Division) This algorithm tries to factor an integer n>1 using trial divisions by an auxiliary sequence of trial divisors.
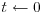 ,
,  .
.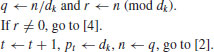
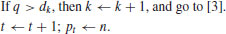
Exercise 4.2 Use Algorithm 4.2 to factor n = 2759; assume that we have the list L of all primes 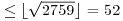 and at least one
and at least one 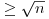 , that is,
, that is,  .
.
Theorem 4.1 Algorithm 4.2 requires a running time in
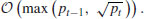
If a primality test between steps [2] and [3] were inserted, the running time would then be in  , or
, or 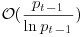 if one does trial division only by primes, where pt−1 is the second largest prime factor of n.
if one does trial division only by primes, where pt−1 is the second largest prime factor of n.
The trial division test is very useful for removing small factors, but it should not be used for factoring completely, except when n is very small, say, for example, n<108.
Algorithm 4.2 seems to be very simple, but its analysis is rather complicated. For example, in order to analyse the average behavior of the algorithm, we will need to know how many trial divisions are necessary and how large the largest prime factor pt will tend to be.
Let 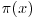 be the primes
be the primes 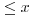 . Then, if the Riemann Hypothesis is true, it would imply that
. Then, if the Riemann Hypothesis is true, it would imply that
(4.4) 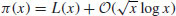
where 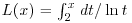 . In 1930, Karl Dickman investigated the probability that a random integer between 1 and x will have its largest prime factor
. In 1930, Karl Dickman investigated the probability that a random integer between 1 and x will have its largest prime factor 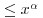 . He gave a heuristic argument to show that this probability approaches the limiting value
. He gave a heuristic argument to show that this probability approaches the limiting value 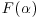 as
as 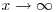 , where f can be calculated from the functional equation
, where f can be calculated from the functional equation
His argument was essentially this: Given 0<t<1, the number of integers less than x whose largest prime factor is between xt and xt + dt is 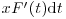 . The number of prime p in that range is
. The number of prime p in that range is
(4.6) 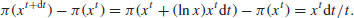
For every such p, the number of integers n such that “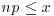 and the largest prime factor of n is
and the largest prime factor of n is 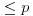 ” is the number of
” is the number of  whose largest prime factor is
whose largest prime factor is 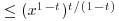 , namely x1−tF(t/(1−t)). Hence
, namely x1−tF(t/(1−t)). Hence 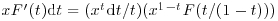 and (4.5) follows by integration.
and (4.5) follows by integration.
If 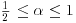 , formula (4.5) simplifies to
, formula (4.5) simplifies to
(4.7) 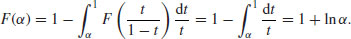
Thus, for example, the probability that a random positive integer 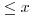 has a prime factor
has a prime factor 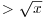 is
is 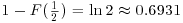 , In all such cases, Algorithm 4.2 must work hard. So, practically, Algorithm 4.2 will give the answer rather quickly if we want to factor a 6-digit integer; but for large n, the amount of computer time for factoring by trial division will rapidly exceed practical limits, unless we are unusually lucky. The algorithm usually finds a few small factors and then begins a long-drawn-out search for the large ones that are left. Interested readers are referred to [4] for more detailed discussion.
, In all such cases, Algorithm 4.2 must work hard. So, practically, Algorithm 4.2 will give the answer rather quickly if we want to factor a 6-digit integer; but for large n, the amount of computer time for factoring by trial division will rapidly exceed practical limits, unless we are unusually lucky. The algorithm usually finds a few small factors and then begins a long-drawn-out search for the large ones that are left. Interested readers are referred to [4] for more detailed discussion.
By an argument analogous to Dickman’s, it has been shown that the second largest prime factor of a random integer x will be 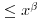 with approximate probability
with approximate probability 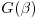 , where
, where
(4.8) 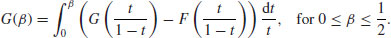
Clearly, 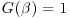 for
for 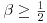 .
.
The total number of prime factors, t is obviously 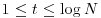 , but these lower and upper bounds are seldom achieved. It is possible to prove that if n is chosen at random between 1 and x, the probability that
, but these lower and upper bounds are seldom achieved. It is possible to prove that if n is chosen at random between 1 and x, the probability that 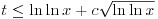 approaches
approaches
(4.9) 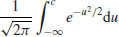
as  , for any fixed c. In other words, the distribution of t is essentially normal, with mean and variance ln ln x; about 99.73 % of all the large integers
, for any fixed c. In other words, the distribution of t is essentially normal, with mean and variance ln ln x; about 99.73 % of all the large integers  have
have  . Furthermore, the average value of t−ln ln x for
. Furthermore, the average value of t−ln ln x for 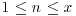 is known to approach
is known to approach
(4.10) 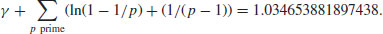
It follows from the above analysis that Algorithm 4.2 will be useful for factoring a 6-digit integer, or a large integer with small prime factors. Fortunately, many more efficient factorization algorithms have been developed since 1980, requiring fewer bit operations than the trial division method; with the fastest being the Number Field Sieve (NFS), which will be discussed later.
Problems for Subsection 4.2
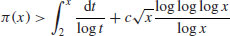
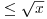 ?
?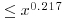 ?
?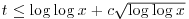 for any fixed c, as
for any fixed c, as 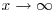 ?
?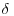 be the number defined by
be the number defined by 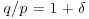 such that
such that 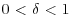 . Show that the number of steps used in the Fermat factoring method is approximately
. Show that the number of steps used in the Fermat factoring method is approximately 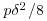 .
.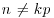 for
for 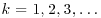 . Show that the number of solutions of (x, y) to
. Show that the number of solutions of (x, y) to 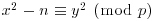 with
with 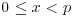 is equal to
is equal to 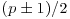 .
.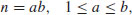
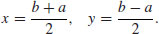
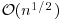 .
.4.3 ρ and p−1 Methods
In 1975 John M. Pollard proposed a very efficient Monte Carlo method [2], now widely known as Pollard’s “rho” or  Method, for finding a small nontrivial factor d of a large integer n. Trial division by all integers up to
Method, for finding a small nontrivial factor d of a large integer n. Trial division by all integers up to 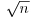 is guaranteed to factor completely any number up to n. For the same amount of work, Pollard’s “rho” Method will factor any number up to n2 (unless we are unlucky).
is guaranteed to factor completely any number up to n. For the same amount of work, Pollard’s “rho” Method will factor any number up to n2 (unless we are unlucky).
The method uses an iteration of the form
(4.11) 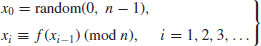
where x0 is a random starting value, n is the number to be factored, and 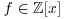 is a polynomial with integer coefficients; usually, we just simply choose
is a polynomial with integer coefficients; usually, we just simply choose 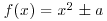 with
with  . Then starting with some initial value x0, a “random” sequence
. Then starting with some initial value x0, a “random” sequence 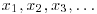 is computed modulo n in the following way:
is computed modulo n in the following way:
(4.12) 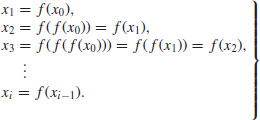
Let d be a nontrivial divisor of n, where d is small compared with n. Since there are relatively few congruence classes modulo d (namely, d of them), there will probably exist integers xi and xj which lie in the same congruence class modulo d, but belong to different classes modulo n; in short, we will have
(4.13) 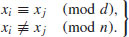
Since 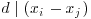 and
and 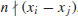 , it follows that
, it follows that  is a nontrivial factor of n. In practice, a divisor d of n is not known in advance, but it can most likely be detected by keeping track of the integers xi, which we do know; we simply compare xi with the earlier xj, calculating
is a nontrivial factor of n. In practice, a divisor d of n is not known in advance, but it can most likely be detected by keeping track of the integers xi, which we do know; we simply compare xi with the earlier xj, calculating 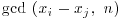 until a nontrivial gcd occurs. The divisor obtained in this way is not necessarily the smallest factor of n and indeed it may not be prime. The possibility exists that when a gcd greater that 1 is found, it may also turn out to be equal to n itself, though this happens very rarely.
until a nontrivial gcd occurs. The divisor obtained in this way is not necessarily the smallest factor of n and indeed it may not be prime. The possibility exists that when a gcd greater that 1 is found, it may also turn out to be equal to n itself, though this happens very rarely.
Example 4.1 For example, let  , f(x) = x2−1 and x1 = 2. Then the “random” sequence
, f(x) = x2−1 and x1 = 2. Then the “random” sequence 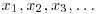 is as follows:
is as follows:
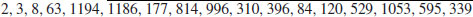
where the repeated values are overlined. Now we find that
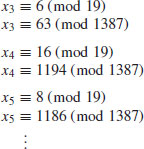
So we have
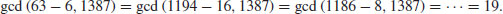
Of course, as mentioned earlier, d is not known in advance, but we can keep track of the integers xi which we do know, and simply compare xi with all the previous xj with j<i, calculating 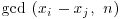 until a nontrivial gcd occurs:
until a nontrivial gcd occurs:
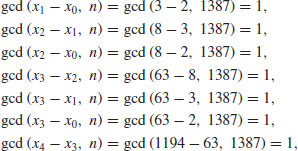
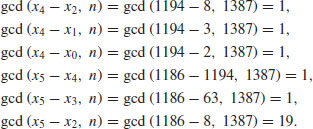
So after 13 comparisons and calculations, we eventually find the divisor 19.
As k increases, the task of computing 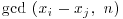 for all j<i becomes very time-consuming; for n = 1050, the computation of
for all j<i becomes very time-consuming; for n = 1050, the computation of 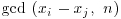 would require about
would require about 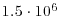 bit operations, as the complexity for computing one gcd is
bit operations, as the complexity for computing one gcd is 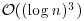 . Pollard actually used Floyd’s method to detect a cycle in a long sequence
. Pollard actually used Floyd’s method to detect a cycle in a long sequence 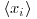 , which just looks at cases in which xi = x2i. To see how it works, suppose that
, which just looks at cases in which xi = x2i. To see how it works, suppose that 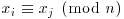 , then
, then
(4.14) 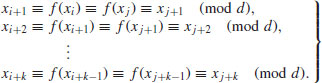
If k = j−i, then  . Hence, we only need look at x2i−xi (or xi−x2i) for
. Hence, we only need look at x2i−xi (or xi−x2i) for 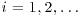 . That is, we only need to check one gcd for each i. Note that the sequence
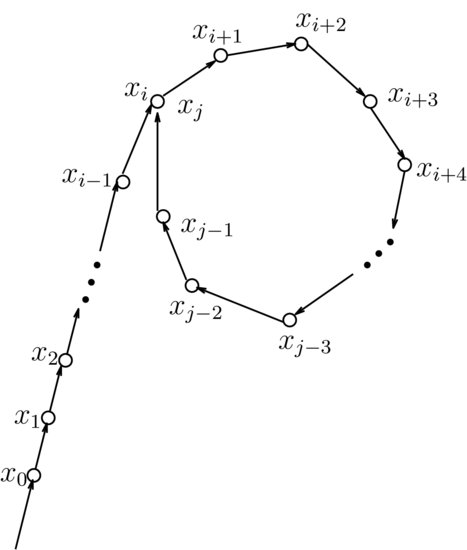
. That is, we only need to check one gcd for each i. Note that the sequence 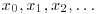 modulo a prime number p, say, looks like a circle with a tail; it is from this behavior that the method gets its name (see Figure 4.2 for a graphical sketch; it looks like the Greek letter
modulo a prime number p, say, looks like a circle with a tail; it is from this behavior that the method gets its name (see Figure 4.2 for a graphical sketch; it looks like the Greek letter 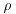 ).
).
Figure 4.2 Illustration of the  Method
Method
Example 4.2 Again, let 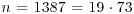 , f(x) = x2−1, and x1 = 2. By comparing pairs xi and x2i, for
, f(x) = x2−1, and x1 = 2. By comparing pairs xi and x2i, for 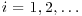 , we have:
, we have:
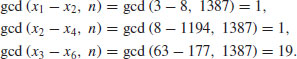
So after only three comparisons and gcd calculations, the divisor 19 of 1387 is found.
In what follows, we shall show that to compute yi = x2i, we do not need to compute 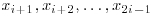 until we get x2i. Observe that
until we get x2i. Observe that
(4.15) 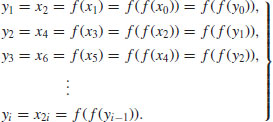
So at each step, we compute
(4.16) 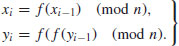
Therefore, only three evaluations of f will be required.
Example 4.3 Let once again 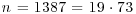 , f(x) = x2−1, and x0 = y0 = 2. By comparing pairs xi and x2i, for
, f(x) = x2−1, and x0 = y0 = 2. By comparing pairs xi and x2i, for 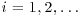 , we get:
, we get:
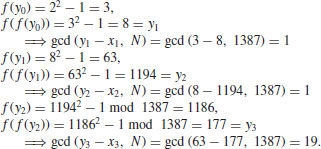
The divisor 19 of 1387 is then found.
Remark 4.1 There is an even more efficient algorithm, due to Richard Brent [3], that looks only at the following differences and the corresponding gcd results:
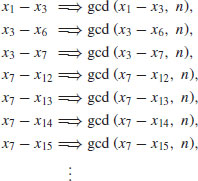
and in general:
(4.17) 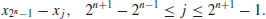
Brent’s algorithm is about 24% faster than Pollard’s original version.
Now we are in a position to present an algorithm for the 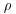 Method.
Method.
Algorithm 4.3 (Brent–Pollard’s 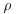 Method) Let n be a composite integer greater than 1. This algorithm tries to find a nontrivial factor d of n, which is small compared to
Method) Let n be a composite integer greater than 1. This algorithm tries to find a nontrivial factor d of n, which is small compared to 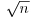 . Suppose the polynomial to use is f(x) = x2 + 1.
. Suppose the polynomial to use is f(x) = x2 + 1.
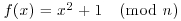 . Choose also a value for t not much bigger than
. Choose also a value for t not much bigger than 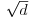 , perhaps
, perhaps 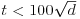 .
.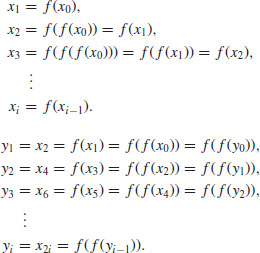
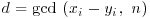 .
.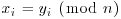 for some i or
for some i or 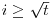 , then go to Step [1] to choose a new seed and a new generator and repeat.
, then go to Step [1] to choose a new seed and a new generator and repeat.Example 4.4 The 8th Fermat number 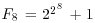 was factored by Brent and Pollard in 1980 by using Brent–Pollard’s “rho” Method:
was factored by Brent and Pollard in 1980 by using Brent–Pollard’s “rho” Method:
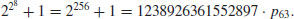
Now let us move to consider the complexity of the 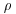 Method. Let p be the smallest prime factor of n, and j the smallest positive index such that
Method. Let p be the smallest prime factor of n, and j the smallest positive index such that 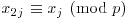 . Making some plausible assumptions, it is easy to show that the expected value of j is
. Making some plausible assumptions, it is easy to show that the expected value of j is  . The argument is related to the well-known “birthday” paradox: Suppose that
. The argument is related to the well-known “birthday” paradox: Suppose that 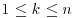 and that the numbers
and that the numbers 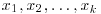 are independently chosen from the set
are independently chosen from the set 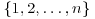 . Then the probability that the numbers xk are distinct is
. Then the probability that the numbers xk are distinct is
(4.18) 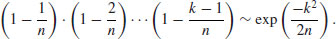
Note that the xi’s are likely to be distinct if k is small compared with 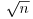 , but unlikely to be distinct if k is large compared with
, but unlikely to be distinct if k is large compared with 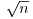 . Of course, we cannot work out
. Of course, we cannot work out 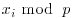 , since we do not know p in advance, but we can detect xj by taking greatest common divisors. We simply compute
, since we do not know p in advance, but we can detect xj by taking greatest common divisors. We simply compute 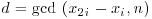 for
for 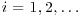 and stop when a d>1 is found.
and stop when a d>1 is found.
Conjecture 4.1 (Complexity of the 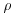 Method) Let p be a prime dividing n and
Method) Let p be a prime dividing n and 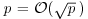 , then the
, then the 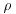 algorithm has expected running time
algorithm has expected running time
(4.19) 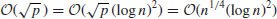
to find the prime factor p of n.
Remark 4.2 The  Method is an improvement over trial division, because in trial division,
Method is an improvement over trial division, because in trial division,  divisions are needed to find a small factor p of n. But of course, one disadvantage of the
divisions are needed to find a small factor p of n. But of course, one disadvantage of the 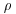 algorithm is that its running time is only a conjectured expected value, not a rigorous bound.
algorithm is that its running time is only a conjectured expected value, not a rigorous bound.
In 1974, Pollard [40] also invented another simple but effective factoring algorithm, now widely known as Pollard’s “p−1” Method, which can be described as follows:
Algorithm 4.4 (Pollard’s “p−1” Method) Let n>1 be a composite number. This algorithm attempts to find a nontrivial factor of n.
 at random. Select a positive integer k that is divisible by many prime powers, for example,
at random. Select a positive integer k that is divisible by many prime powers, for example, 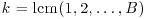 for a suitable bound B (the larger B is the more likely the method will be to succeed in producing a factor, but the longer the method will take to work).
for a suitable bound B (the larger B is the more likely the method will be to succeed in producing a factor, but the longer the method will take to work).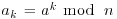 .
.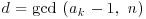 .
.The “p−1” algorithm is usually successful in the fortunate case where n has a prime divisor p for which p−1 has no large prime factors. Suppose that 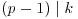 and that
and that 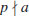 . Since
. Since  , we have
, we have 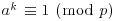 , thus
, thus  . In many cases, we have
. In many cases, we have 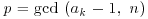 , so the method finds a nontrivial factor of n.
, so the method finds a nontrivial factor of n.
Example 4.5 Use the “p−1” Method to factor the number n = 540143. Choose B = 8 and hence k = 840. Choose also a = 2. Then we have
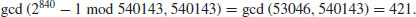
Thus 421 is a (prime) factor of 540143. In fact, 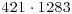 is the complete prime factorization of 540143. It is interesting to note that by using the “p−1” method Baillie in 1980 found the prime factor
is the complete prime factorization of 540143. It is interesting to note that by using the “p−1” method Baillie in 1980 found the prime factor
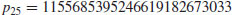
of the Mersenne number M257 = 2257−1. In this case
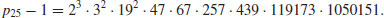
In the worst case, where (p−1)/2 is prime, the “p−1” algorithm is no better than trial division. Since the group has fixed order p−1 there is nothing to be done except try a different algorithm. Note that there is a similar method to “p−1,” called “p + 1,” that was proposed by H. C. Williams in 1982. It is suitable for the case where n has a prime factor p for which p + 1 has no large prime factors.
Problems for Section 4.3
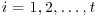 ,
, 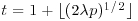 for a given real number
for a given real number 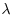 . Show that the probability
. Show that the probability  are pairwise different
are pairwise different 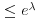 .
.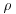 Method for factoring a general number n is
Method for factoring a general number n is 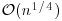 .
.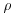 Method to factor n.
Method to factor n.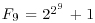 .
. Factoring Method to factor 4087 using x0 = 2 and f(x) = x2−1.
Factoring Method to factor 4087 using x0 = 2 and f(x) = x2−1.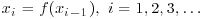 . Let also t, u>0 be the smallest numbers in the sequence
. Let also t, u>0 be the smallest numbers in the sequence 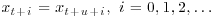 , where t and u are called the lengths of the
, where t and u are called the lengths of the  tail and cycle, respectively. Give an efficient algorithm to determine t and u exactly, and analyze the running time of your algorithm.
tail and cycle, respectively. Give an efficient algorithm to determine t and u exactly, and analyze the running time of your algorithm.4.4 Elliptic Curve Method
In this section, we shall introduce a factoring method depending on the use of elliptic curves. The method is actually obtained from Pollard’s “p−1” algorithm: If we can choose a random group G with order G close to p, we may be able to perform a computation similar to that involved in Pollard’s “p−1” algorithm, working in G rather than in Fp. If all prime factors of G are less than the bound B then we find a factor of n. Otherwise, we repeat this procedure with a different group G (and hence, usually, a different G) until a factor is found. This is the motivation of the ECM method, invented by H. W. Lenstra in 1987 [42].
Algorithm 4.5 (Lenstra’s Elliptic Curve Method) Let n>1 be a composite number, with 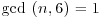 . This algorithm attempts to find a nontrivial factor of n. The method depends on the use of elliptic curves and is the analog to Pollard’s “p−1” Method.
. This algorithm attempts to find a nontrivial factor of n. The method depends on the use of elliptic curves and is the analog to Pollard’s “p−1” Method.
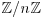 , and
, and 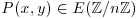 is a point on e. That is, choose
is a point on e. That is, choose 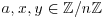 at random, and set
at random, and set 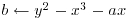 . If
. If 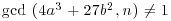 , then e is not an elliptic curve, start all over and choose another pair (E, P).
, then e is not an elliptic curve, start all over and choose another pair (E, P).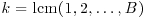 or k = B! for a suitable bound B; the larger B is the more likely the method will succeed in producing a factor, but the longer the method will take to work.
or k = B! for a suitable bound B; the larger B is the more likely the method will succeed in producing a factor, but the longer the method will take to work.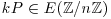 . We use the following formula to compute P3(x3, y3) = P1(x1, y1) + P2(x2, y2) modulo n:
. We use the following formula to compute P3(x3, y3) = P1(x1, y1) + P2(x2, y2) modulo n: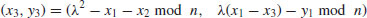
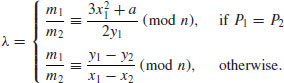
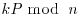 can be done in
can be done in 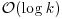 doublings and additions.
doublings and additions.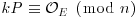 , then compute
, then compute  , else go to Step [1] to make a new choice for “a” or even for a new pair (E, P).
, else go to Step [1] to make a new choice for “a” or even for a new pair (E, P).As for the “p−1” method, one can show that a given pair (E, P) is likely to be successful in the above algorithm if n has a prime factor p for which  is composed of small primes only. The probability for this to happen increases with the number of pairs (E, P) that one tries.
is composed of small primes only. The probability for this to happen increases with the number of pairs (E, P) that one tries.
Example 4.6 Use the ECM method to factor the number n = 187.
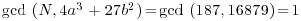 (note that here a = 1 and b = 25).
(note that here a = 1 and b = 25).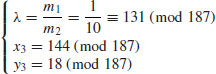
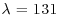 .
.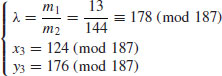
 .
.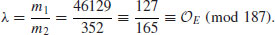
 . Since 1<11<187, 11 is a (prime) factor of 187. In fact,
. Since 1<11<187, 11 is a (prime) factor of 187. In fact,  .
.Example 4.7 To factor n = 7560636089, we calculate kP = k(1, 3) with  on
on 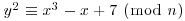 :
:
| 3P = (1329185554, 395213649) | 6P = (646076693, 5714212282) |
| 12P = (5471830359, 5103472059) | 24P = (04270711, 3729197625) |
| 49P = (326178740, 3033431040) | 99P = (5140727517, 2482333384) |
| 199P = (1075608203, 3158750830) | 398P = (4900089049, 2668152272) |
| 797P = (243200145, 2284975169) | 1595P = (3858922333, 4843162438) |
| 3191P = (7550557590, 1472275078) | 6382P = (4680335599, 1331171175) |
| 12765P = (6687327444, 7233749859) | 25530P = (6652513841, 6306817073) |
| 51061P = (6578825631, 5517394034) | 102123P = (1383310127, 2036899446) |
| 204247P = (3138092894, 2918615751) | 408495P = (6052513220, 1280964400) |
| 816990P = (2660742654, 3418862519) | 1633980P = (7023086430, 1556397347) |
| 3267961P = (5398595429, 795490222) | 6535923P = (4999132, 4591063762) |
| 13071847P = (3972919246, 7322445069) | 26143695P = (3597132904, 3966259569) |
| 52287391P = (2477960886, 862860073) | 104574782P = (658268732, 3654016834) |
| 209149565P = (6484065460, 287965264) | 418299131P = (1622459893, 4833264668) |
| 836598262P = (7162984288, 487850179) | 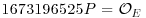 . . |
Now, 1673196525P is the point at infinity since 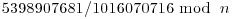 is impossible. Hence,
is impossible. Hence,  gives a factor of n.
gives a factor of n.
Example 4.8 The following are some ECM factoring examples. In 1995 Richard Brent at the Australian National University completed the factorization of the 10th Fermat number using ECM:
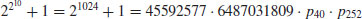
where the 40-digit prime p40 was found using ECM, and p252 was proved to be a 252-digit prime. Brent also completed the factorization of the 11th Fermat number (with 617-digit) 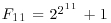 using ECM:
using ECM:
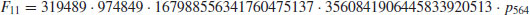
where the 21-digit and 22-digit prime factors were found using ECM, and p564 is a 564-digit prime. Other recent ECM-records include a 38-digit prime factor (found by A. K. Lenstra and M. S. Manasse) in the 112-digit composite 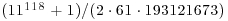 , a 40-digit prime factor of 26126 + 1, a 43-digit prime factor of the partition number p(19997), and a 44-digit prime factor of the partition number p(19069) in the RSA Factoring Challenge List, and a 47-digit prime in c135 of
, a 40-digit prime factor of 26126 + 1, a 43-digit prime factor of the partition number p(19997), and a 44-digit prime factor of the partition number p(19069) in the RSA Factoring Challenge List, and a 47-digit prime in c135 of  .
.
Both Lenstra’s ECM algorithm and Pollard’s “p−1” algorithm can be sped up by the addition of a second phase. The idea of the second phase in ECM is to find a factor in the case that the first phase terminates with a group element  , such that
, such that 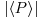 is reasonably small, say
is reasonably small, say 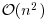 ), here
), here 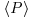 is the cyclic group generated by p. There are several possible implementations of the second phase. One of the simplest uses a pseudorandom walk in
is the cyclic group generated by p. There are several possible implementations of the second phase. One of the simplest uses a pseudorandom walk in 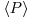 . By the birthday paradox argument, there is a good chance that two points in the random walk will coincide after
. By the birthday paradox argument, there is a good chance that two points in the random walk will coincide after 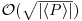 steps, and when this occurs a nontrivial factor of n can usually be found (see [6] and [5] for more detailed information on the implementation issues of the ECM.
steps, and when this occurs a nontrivial factor of n can usually be found (see [6] and [5] for more detailed information on the implementation issues of the ECM.
Conjecture 4.2 (Complexity of the ECM method) Let p be the smallest prime dividing n. Then the ECM method will find p of n, under some plausible assumptions, in expected running time
(4.20) 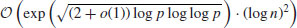
In the worst case, when n is the product of two prime factors of the same order of magnitude, we have
(4.21) 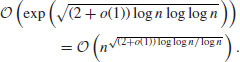
Remark 4.3 The most interesting feature of ECM is that its running time depends very much on p (the factor found) of n, rather than n itself. So one advantage of the ECM is that one may use it, in a manner similar to trial divisions, to locate the smaller prime factors p of a number n which is much too large to factor completely.
Problems for Section 4.4
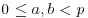 , for which
, for which 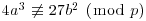 is exactly p2−p.
is exactly p2−p.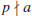 , then the root r of the congruence
, then the root r of the congruence 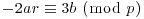 is a repeated rood modulo p of the polynomial x3−ax−b.
is a repeated rood modulo p of the polynomial x3−ax−b.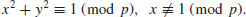

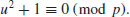
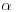 is a real number, then the probability that a random positive integer
is a real number, then the probability that a random positive integer 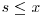 has all its prime factors
has all its prime factors 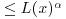 is
is 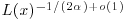 for
for 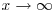 , where
, where 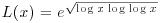 with x a real number >e.
with x a real number >e.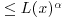 in the small interval
in the small interval 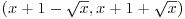 is
is 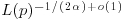 for
for 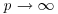 .
.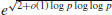
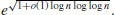
4.5 Continued Fraction Method
The Continued Fraction Method is perhaps the first modern, general purpose integer factorization method, although its original idea may go back to M. Kraitchik in the 1920s, or even earlier to A. M. Legendre. It was used by D. H. Lehmer and R. E. Powers to devise a new technique in the 1930s, however the method was not very useful and applicable at the time because it was unsuitable for desk calculators. About 40 years later, it was first implemented on a computer by M. A. Morrison and J. Brillhart [7], who used it to successfully factor the seventh Fermat number
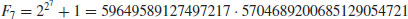
on the morning of 13 September 1970.
The Continued FRACtion (CFRAC) method looks for small values of |W| such that 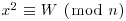 has a solution. Since W is small (specifically
has a solution. Since W is small (specifically 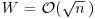 ), it has a reasonably good chance of being a product of primes in our factor base FB. Now if W is small and
), it has a reasonably good chance of being a product of primes in our factor base FB. Now if W is small and 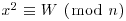 , then we can write x2 = W + knd2 for some k and d, hence (x/d)2−kn = W/d2 will be small. In other words, the rational number x/d is an approximation of
, then we can write x2 = W + knd2 for some k and d, hence (x/d)2−kn = W/d2 will be small. In other words, the rational number x/d is an approximation of 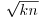 . This suggests looking at the continued fraction expansion of
. This suggests looking at the continued fraction expansion of 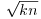 , since continued fraction expansions of real numbers give good rational approximations. This is exactly the idea behind the CFRAC method! We first obtain a sequence of approximations (i.e., convergents) Pi/Qi to
, since continued fraction expansions of real numbers give good rational approximations. This is exactly the idea behind the CFRAC method! We first obtain a sequence of approximations (i.e., convergents) Pi/Qi to 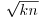 for a number of values of k, such that
for a number of values of k, such that
(4.22) 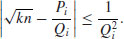
Putting Wi = P2i−Q2ikn, then we have
(4.23) 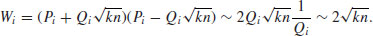
Hence, the 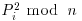 are small and more likely to be smooth, as desired. Then, we try to factor the corresponding integers Wi = P2i−Q2ikn over our factor base FB; with each success, we obtain a new congruence of the form
are small and more likely to be smooth, as desired. Then, we try to factor the corresponding integers Wi = P2i−Q2ikn over our factor base FB; with each success, we obtain a new congruence of the form
Once we have obtained at least m + 2 such congruences, by Gaussian elimination over 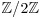 we have obtained a congruence
we have obtained a congruence 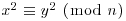 . That is, if (x1, e01, e11, ···, em1), ···, (xr, e0r, e1r, ···, emr) are solutions of (4.24) such that the vector sum
. That is, if (x1, e01, e11, ···, em1), ···, (xr, e0r, e1r, ···, emr) are solutions of (4.24) such that the vector sum
is even in each component, then
(4.26) 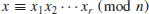
(4.27) 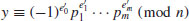
is a solution to
(4.28) 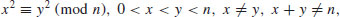
except for the possibility that 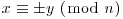 , and hence (usually) a nontrivial factoring of n, by computing
, and hence (usually) a nontrivial factoring of n, by computing 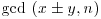 .
.
Example 4.9 We now illustrate, by an example, the idea of CFRAC factoring. Let n = 1037. Then  . The first ten continued fraction approximations of
. The first ten continued fraction approximations of 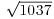 are:
are:
| Convergent P/Q | 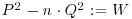
|
| 32/1 | −13 = −13 |
| 129/4 | 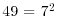
|
| 161/5 | 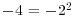
|

|
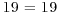
|
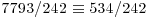
|
−19 = −19 |
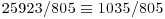
|
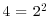
|
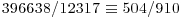
|
−49 = −72 |
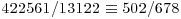
|
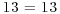
|
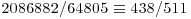
|
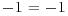
|
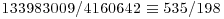
|
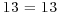
|
Now we search for squares on both sides, either just by a single congruence, or by a combination (i.e., multiplying together) of several congruences and find that
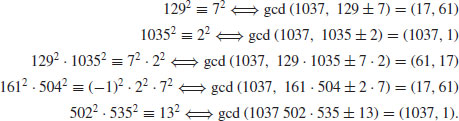
Three of them yield a factorization of 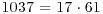 .
.
It is clear that the CFRAC factoring algorithm is essentially just a continued fraction algorithm for finding the continued fraction expansion [q0, q1, ···, qk, ···] of  , or the Pk and Qk of such an expansion. In what follows, we shall briefly summarize the CFRAC method just discussed above in the following algorithmic form:
, or the Pk and Qk of such an expansion. In what follows, we shall briefly summarize the CFRAC method just discussed above in the following algorithmic form:
Algorithm 4.6 (CFRAC factoring) Given a positive integer n and a positive integer k such that kn is not a perfect square, this algorithm tries to find a factor of n by computing the continued fraction expansion of 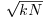 .
.
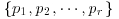 chosen such that it is possible to find some integer xi such that
chosen such that it is possible to find some integer xi such that 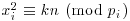 . Usually, FB contains all such primes less than or equal to some limit. Note that the multiplier k>1 is needed only when the period is short. For example, Morrison and Brillhart used k = 257 in factoring F7.
. Usually, FB contains all such primes less than or equal to some limit. Note that the multiplier k>1 is needed only when the period is short. For example, Morrison and Brillhart used k = 257 in factoring F7.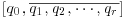 of
of 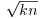 for a number of values of k. This gives us good rational approximations P/Q. The recursion formulas to use for computing P/Q are as follows:
for a number of values of k. This gives us good rational approximations P/Q. The recursion formulas to use for computing P/Q are as follows: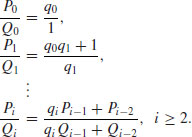
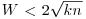 , each of these W is only about half the length of kn. If we succeed, we get a new congruence. For each success, we obtain a congruence
, each of these W is only about half the length of kn. If we succeed, we get a new congruence. For each success, we obtain a congruence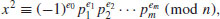
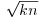 and
and  , then
, then(4.29) 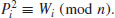
 we obtain a congruence
we obtain a congruence 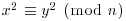 . That is, if (x1, e01, e11, ···, em1), ···, (xr, e0r, e1r, ···, emr) are solutions of (4.24) such that the vector sum defined in (4.25) is even in each component, then
. That is, if (x1, e01, e11, ···, em1), ···, (xr, e0r, e1r, ···, emr) are solutions of (4.24) such that the vector sum defined in (4.25) is even in each component, then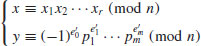
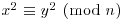 , except for the possibility that
, except for the possibility that 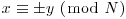 , and hence we have
, and hence we have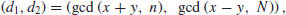
Conjecture 4.3 (The complexity of the CFRAC Method) If n is the integer to be factored, then under certain reasonable heuristic assumptions, the CFRAC method will factor n in time
(4.30) 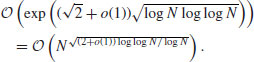
Remark 4.4 This is a conjecture, not a theorem, because it is supported by some heuristic assumptions which have not been proven.
Problems for Section 4.5

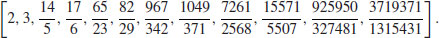
 . Then
. Then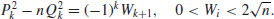
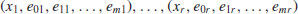
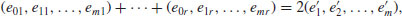
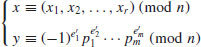
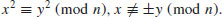

4.6 Quadratic Sieve
The idea of the quadratic sieve (QS) was first introduced by Carl Pomerance in 1982 [8]. QS is somewhat similar to CFRAC except that instead of using continued fractions to produce the values for  , it uses expressions of the form
, it uses expressions of the form
(4.32) 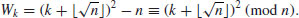
Here, if 0<k<L, then
(4.33) 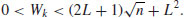
If we get
then we have 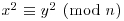 with
with
(4.35) 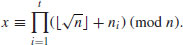
Once such x and y are found, there is a good chance that 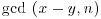 is a nontrivial factor of n.
is a nontrivial factor of n.
Example 4.10 Use the Quadratic Sieve Method (QS) to factor n = 2041. Let W(x) = x2−n, with x = 43, 44, 45, 46. Then we have:

which leads to the following congruence:
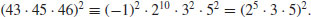
This congruence gives the factorization of 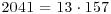 , since
, since
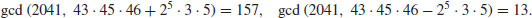
For the purpose of implementation, we can use the same set FB as that used in CFRAC and the same idea as that described above to arrange (4.34) to hold.
The most widely used variation of the quadratic sieve is perhaps the Multiple Polynomial Quadratic Sieve (MPQS), first proposed by Peter Montgomery in 1986. The idea of the MPQS is as follows: To find the (x, y) pair in
we try to find triples (Ui, Vi, Wi), for 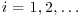 , such that
, such that
where W is easy to factor (at least easier than n). If sufficiently many congruences (4.37) are found, they can be combined, by multiplying together a subset of them, in order to get a relation of the form (4.36). The version of the MPQS algorithm described here is based on [9].
Algorithm 4.7 (Multiple Polynomial Quadratic Sieve) Given a positive integer n>1, this algorithm will try to find a factor n using the multiple polynomial quadratic sieve.
 , such that a, b, c satisfy the following relations:
, such that a, b, c satisfy the following relations:(4.38) 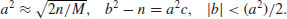
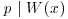 , then
, then(4.39) 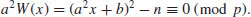
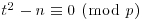 should be solvable. So, the factor base FB (consisting of all primes less than a bound B) should be chosen in such a way that
should be solvable. So, the factor base FB (consisting of all primes less than a bound B) should be chosen in such a way that  is solvable. There are L primes pj,
is solvable. There are L primes pj, 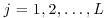 in FB; this set of primes is fixed in the whole factoring process.
in FB; this set of primes is fixed in the whole factoring process.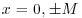 such that
such that  . If
. If  , then
, then  , thus W(x) is easier to factor than n.
, thus W(x) is easier to factor than n.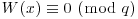 for all q = pe<B, for all primes
for all q = pe<B, for all primes 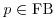 , and save the solutions for each q.
, and save the solutions for each q.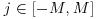 , for which
, for which 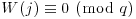 , for all q = pe<B, and for all primes
, for all q = pe<B, and for all primes 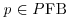 .
.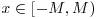 for which W(x) is only composed of prime factors <B.
for which W(x) is only composed of prime factors <B.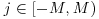 for which SI(j) is closed to
for which SI(j) is closed to 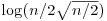 .
. ,
,(4.41) 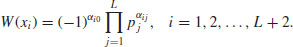
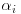 as follows
as follows(4.42) 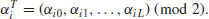
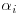 (at least L + 2) than components (L + 1), there exists at least one subset s of the set
(at least L + 2) than components (L + 1), there exists at least one subset s of the set 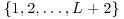 such that
such that(4.43) 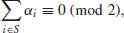
(4.44) 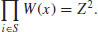
(4.45) 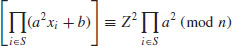
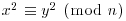 .
.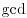 .
.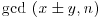 to find the prime factors of n.
to find the prime factors of n.Example 4.11 MPQS has been used to obtain many spectacular factorizations. One such factorization is the 103-digit composite number
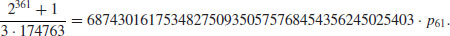
The other record of the MPQS is the factorization of the RSA-129 in April 1994, a 129 digit composite number:

It was estimated in Gardner [23] in 1977 that the running time required to factor numbers with about the same size as RSA-129 would be about 40 quadrillion years using the best algorithm and fastest computer at that time. It was factorized by Derek Atkins, Michael Graff, Arjen Lenstra, Paul Leyland, and more than 600 volunteers from more than 20 countries, on all continents except Antarctica. To factor this number, they used the double large prime variation of the Multiple Polynomial Quadratic Sieve Factoring Method. The sieving step took approximately 5000 mips years.
Conjecture 4.4 (The complexity of the QS/MPQS Method) If n is the integer to be factored, then under certain reasonable heuristic assumptions, the QS/MPQS method will factor n in time
(4.46) 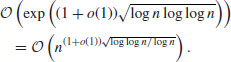
Problems for Section 4.6
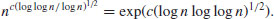
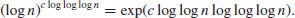
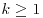 , then
, then 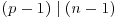 .
.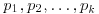 are distinct odd primes. Let also
are distinct odd primes. Let also  . Then the congruence
. Then the congruence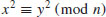
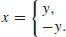
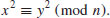
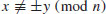

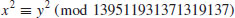
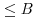 . Let
. Let 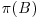 the numbers of primes in the interval [1, B] and
the numbers of primes in the interval [1, B] and 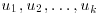 be positive B-smooth integers with
be positive B-smooth integers with 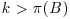 . Show that some nonempty subset of
. Show that some nonempty subset of 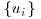 has product which is a square.
has product which is a square. be an arbitrary small positive integer, and
be an arbitrary small positive integer, and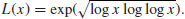
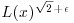 is chosen from [1, x] independently and uniformly, then the probability that some nonempty subset product is a square tends to 1 as
is chosen from [1, x] independently and uniformly, then the probability that some nonempty subset product is a square tends to 1 as 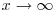 , whereas the probability that some nonempty subset product is a square tends to 0 as
, whereas the probability that some nonempty subset product is a square tends to 0 as 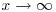 if
if 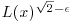 is chosen.
is chosen.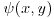 be y-smooth numbers up to x. Show that the expected number of choices of random integers in [1, x] to find one y-smooth number is
be y-smooth numbers up to x. Show that the expected number of choices of random integers in [1, x] to find one y-smooth number is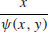
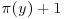 such y-smooth numbers is
such y-smooth numbers is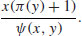
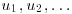 be y-smooth number, and let each be factored as follows
be y-smooth number, and let each be factored as follows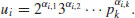

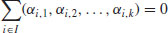
 . Moreover, such a nontrivial subset is guaranteed amongst
. Moreover, such a nontrivial subset is guaranteed amongst 
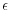 be any fixed, positive real number. Show that
be any fixed, positive real number. Show that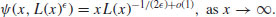
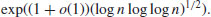
4.7 Number Field Sieve
Before introducing the Number Field Sieve (NFS), it is interesting to briefly review some important milestones in the development of the factoring methods. In 1970, it was barely possible to factor “hard” 20-digit numbers. In 1980, by using the CFRAC method, factoring of 50-digit numbers was becoming commonplace. In 1990, the QS method had doubled the length of the numbers that could be factored by CFRAC, with a record having 116 digits. In the spring of 1996, the NFS method had successfully split a 130-digit RSA challenge number in about 15% of the time the QS would have taken. At present, the Number Field Sieve (NFS) is the champion of all known factoring methods. NFS was first proposed by John Pollard in a letter to A. M. Odlyzko, dated August 31 1988, with copies to R. P. Brent, J. Brillhart, H. W. Lenstra, C. P. Schnorr, and H. Suyama, outlining an idea of factoring certain big numbers via algebraic number fields. His original idea was not for any large composite, but for certain “pretty” composites that had the property that they were close to powers. He illustrated the idea with a factorization of the seventh Fermat number 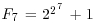 which was first factored by CFRAC in 1970. He also speculated in the letter that “if F9 is still unfactored, then it might be a candidate for this kind of method eventually?” The answer now is of course “yes,” since F9 was factored by using NFS in 1990. It is worthwhile pointing out that NFS is not only a method suitable for factoring numbers in a special form like F9, but also a general purpose factoring method for any integer of a given size. There are, in fact, two forms of NFS (Huizing [10], and Lenstra and Lenstra [11]): the special NFS (SNFS), tailored specifically for integers of the form N = c1rt + c2su, and the general NFS (GNFS), applicable to any arbitrary numbers. Since NFS uses some ideas from algebraic number theory, a brief introduction to some basic concepts of algebraic number theory is in order.
which was first factored by CFRAC in 1970. He also speculated in the letter that “if F9 is still unfactored, then it might be a candidate for this kind of method eventually?” The answer now is of course “yes,” since F9 was factored by using NFS in 1990. It is worthwhile pointing out that NFS is not only a method suitable for factoring numbers in a special form like F9, but also a general purpose factoring method for any integer of a given size. There are, in fact, two forms of NFS (Huizing [10], and Lenstra and Lenstra [11]): the special NFS (SNFS), tailored specifically for integers of the form N = c1rt + c2su, and the general NFS (GNFS), applicable to any arbitrary numbers. Since NFS uses some ideas from algebraic number theory, a brief introduction to some basic concepts of algebraic number theory is in order.
Definition 4.1 A complex number 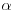 is an algebraic number if it is a root of a polynomial
is an algebraic number if it is a root of a polynomial
(4.47) 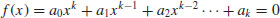
where  and
and 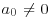 . If f(x) is irreducible over
. If f(x) is irreducible over 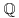 and
and 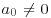 , then k is the degree of x.
, then k is the degree of x.
Example 4.12 Two examples of algebraic numbers are as follows:
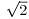 , which is of degree 2 because we can take f(x) = x2−2 = 0 (
, which is of degree 2 because we can take f(x) = x2−2 = 0 (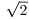 is irrational).
is irrational).Any complex number that is not algebraic is said to be transcendental such as  and e.
and e.
Definition 4.2 A complex number  is an algebraic integer if it is a root of a monic polynomial
is an algebraic integer if it is a root of a monic polynomial
where  .
.
Remark 4.5 A quadratic integer is an algebraic integer satisfying a monic quadratic equation with integer coefficients. A cubic integer is an algebraic integer satisfying a monic cubic equation with integer coefficients.
Example 4.13 Some examples of algebraic integers are as follows:
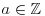 .
. and
and 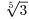 , because they satisfy the monic equations x3−2 = 0 and x3−5 = 0, respectively.
, because they satisfy the monic equations x3−2 = 0 and x3−5 = 0, respectively.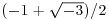 , because it satisfies x2 + x + 1 = 0.
, because it satisfies x2 + x + 1 = 0.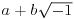 , with
, with 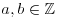 .
.Clearly, every algebraic integer is an algebraic number, but the converse is not true.
Proposition 4.1 A rational number 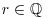 is an algebraic integer if and only if
is an algebraic integer if and only if 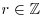 .
.
Proof: If 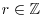 , then r is a root of x−r = 0. Thus r is an algebraic integer Now suppose that
, then r is a root of x−r = 0. Thus r is an algebraic integer Now suppose that 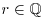 and r is an algebraic integer (i.e., r = c/d is a root of (4.48), where
and r is an algebraic integer (i.e., r = c/d is a root of (4.48), where 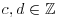 ; we may assume
; we may assume  ). Substituting c/d into (4.48) and multiplying both sides by dn, we get
). Substituting c/d into (4.48) and multiplying both sides by dn, we get
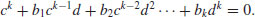
It follows that 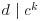 and
and 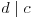 (since
(since 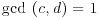 ). Again since
). Again since 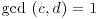 , it follows that
, it follows that 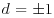 . Hence
. Hence 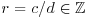 . It follows, for example, that 2/5 is an algebraic number but not an algebraic integer.
. It follows, for example, that 2/5 is an algebraic number but not an algebraic integer.

Remark 4.6 The elements of 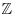 are the only rational numbers that are algebraic integers. We shall refer to the elements of
are the only rational numbers that are algebraic integers. We shall refer to the elements of 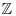 as rational integers when we need to distinguish them from other algebraic integers that are not rational. For example,
as rational integers when we need to distinguish them from other algebraic integers that are not rational. For example, 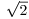 is an algebraic integer but not a rational integer.
is an algebraic integer but not a rational integer.
The most interesting results concerned with the algebraic numbers and algebraic integers are contained in the following theorem.
Theorem 4.2 The set of algebraic numbers forms a field, and the set of algebraic integers forms a ring.
Proof: See pp. 67–68 of Ireland and Rosen [12].

Lemma 4.1 Let f(x) be an irreducible monic polynomial of degree d over integers and M an integer such that 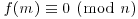 . Let
. Let 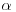 be a complex root of f(x) and
be a complex root of f(x) and 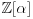 the set of all polynomials in
the set of all polynomials in 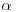 with integer coefficients. Then there exists a unique mapping
with integer coefficients. Then there exists a unique mapping 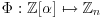 satisfying
satisfying
 ;
; ;
;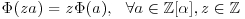 ;
;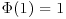 ;
;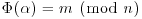 .
.Now we are in a position to introduce the Number Field Sieve (NFS). Note that there are two main types of NFS: NFS (general NFS) for general numbers and SNFS (special NFS) for numbers with special forms. The idea, however, behind the GNFS and SNFS is the same:
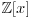 , and an integer M such that
, and an integer M such that 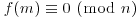 .
. be an algebraic number that is the root of f(x), and denote the set of polynomials in
be an algebraic number that is the root of f(x), and denote the set of polynomials in 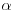 with integer coefficients as
with integer coefficients as 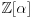 .
.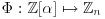 via
via 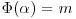 which ensures that for any
which ensures that for any 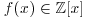 , we have
, we have 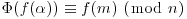 .
.(4.49) 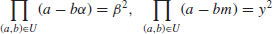
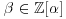 and
and 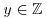 . Let
. Let 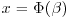 . Then
. Then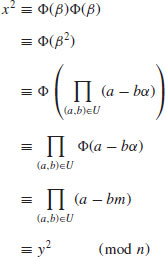
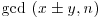 .
.There are many ways to implement the above idea, all of which follow the same pattern as we discussed previously in CFRAC and QS/MPQS: By a sieving process one first tries to find congruences modulo n by working over a factor base, and then does a Gaussian elimination over 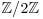 to obtain a congruence of squares
to obtain a congruence of squares 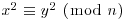 . We give in the following a brief description of the NFS algorithm [13].
. We give in the following a brief description of the NFS algorithm [13].
Algorithm 4.8 Given an odd positive integer n, the NFS algorithm has the following four main steps in factoring n:
(4.50) 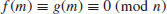
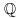 .
.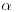 be a complex root of f and
be a complex root of f and 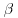 a complex root of G. Find pairs (a, b) with
a complex root of G. Find pairs (a, b) with 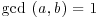 such that the integral norms of
such that the integral norms of 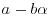 and
and 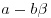 :
:(4.51) 
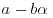 and
and 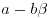 factor into products of prime ideals in the number field
factor into products of prime ideals in the number field 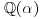 and
and 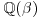 , respectively.)
, respectively.)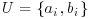 of indices such that the two products
of indices such that the two products(4.53) 
Define 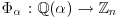 and
and  via
via  , where M is the common root of both f and G. Then
, where M is the common root of both f and G. Then
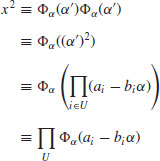
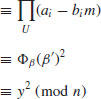
which is of the required form of the factoring congruence, and hopefully, a factor of n can be found by calculating 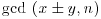 .
.
Example 4.14 We first give a rather simple NFS factoring example. Let 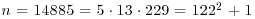 . So we put f(x) = x2 + 1 and m = 122, such that
. So we put f(x) = x2 + 1 and m = 122, such that
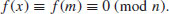
If we choose 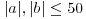 , then we can easily find (by sieving) that
, then we can easily find (by sieving) that
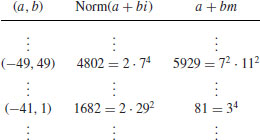
(Readers should be able to find many such pairs of (ai, bi) in the interval, that are smooth up to e.g., 29.) So, we have
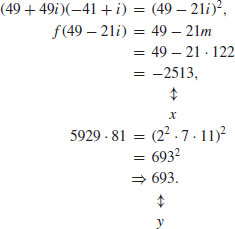
Thus,
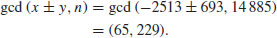
In the same way, if we wish to factor n = 84101 = 2902 + 1, then we let m = 290, and f(x) = x2 + 1 so that
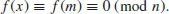
We tabulate the sieving process as follows:
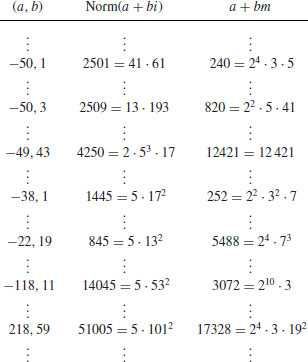
Clearly, −38 + i and −22 + 19i can produce a product square, since
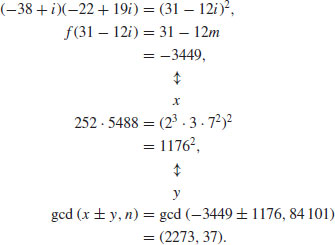
In fact, 84101 = 2273× 37. Note that −118 + 11i and 218 + 59i can also produce a product square, since
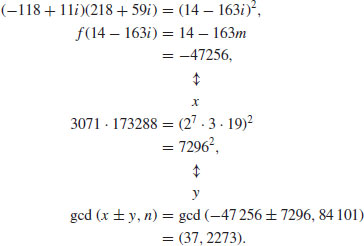
Example 4.15 Next we present a slightly more complicated example. Use NFS to factor n = 1098413. First notice that 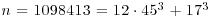 , which is in a special form and can be factored by using SNFS.
, which is in a special form and can be factored by using SNFS.
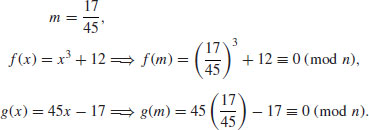
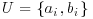 as follows:
as follows: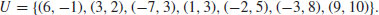
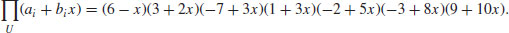
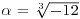 and
and 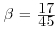 . Then
. Then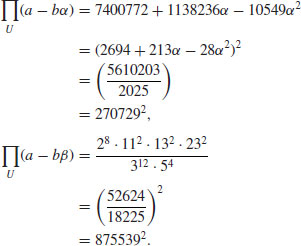
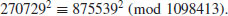
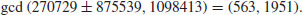
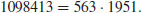
Example 4.16 Finally, we give some large factoring examples using NFS.
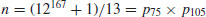
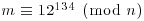 . The factor base bound was 4.8 million for f and 12 million for G. Both large prime bounds were 150 million, with two large primes allowed on each side. They sieved over
. The factor base bound was 4.8 million for f and 12 million for G. Both large prime bounds were 150 million, with two large primes allowed on each side. They sieved over 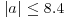 million and
million and 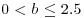 million. The sieving lasted 10.3 calendar days; 85 SGI machines at CWI contributed a combined 13027719 relations in 560 machine-days. It took 1.6 more calendar days to process the data. This processing included 16 CPU-hours on a Cray C90 at SARA in Amsterdam to process a 1969262× 1986500 matrix with 57942503 nonzero entries. The other large number factorized by using SNFS is the 9th Fermat number:
million. The sieving lasted 10.3 calendar days; 85 SGI machines at CWI contributed a combined 13027719 relations in 560 machine-days. It took 1.6 more calendar days to process the data. This processing included 16 CPU-hours on a Cray C90 at SARA in Amsterdam to process a 1969262× 1986500 matrix with 57942503 nonzero entries. The other large number factorized by using SNFS is the 9th Fermat number: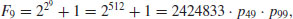
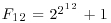 ; we only know its partial prime factorization:
; we only know its partial prime factorization: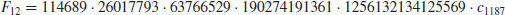

Remark 4.7 Prior to the NFS, all modern factoring methods had an expected running time of at best
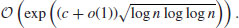
For example, Dixon’s Random Square Method has the expected running time
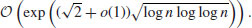
whereas the Multiple Polynomial Quadratic Sieve (MPQS) takes time
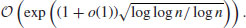
Because of the Canfield-Erdös-Pomerance theorem, some people even believed that this could not be improved upon except maybe for the term (c + o(1)), but the invention of the NFS has changed all this.
Conjecture 4.5 (Complexity of NFS) Under some reasonable heuristic assumptions, the NFS method can factor an integer n in time
(4.54) 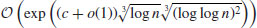
where  if GNFS is used to factor an arbitrary integer n, whereas
if GNFS is used to factor an arbitrary integer n, whereas  if SNFS is used to factor a special integer n.
if SNFS is used to factor a special integer n.
Problems for Section 4.7





4.8 Bibliographic Notes and Further Reading
In this chapter, we discussed some of the most popular algorithms for integer factorization. For general references in this field, it is suggested that readers consult, for example, [14–38].
Shanks’ Square Forms Factorization was studied in [39]. The p−1 Factoring Method was proposed by Pollard in [40] and  Factoring Method in [2], respectively. An improved version of
Factoring Method in [2], respectively. An improved version of 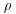 was proposed by Brent in [3]. The p + 1 Factoring Method was proposed by Williams in [41].
was proposed by Brent in [3]. The p + 1 Factoring Method was proposed by Williams in [41].
The ECM factoring method was first proposed by Lenstra in [42]. More information on ECM may be found in [5,6]. The CFRAC factoring method was first proposed and implemented in [7]. The QS factoring method was first proposed by Pomerance in the 1980s [9, 43,44]. The idea of NFS was first proposed by Pollard and subsequently improved by many authors; more information about the NFS can be found in [11, 45,46]. Readers who are interested in parallel and distributed factoring may consult [47–50].
References
1. P. Shor, “Polynomial-Time Algorithms for Prime Factorization and Discrete Logarithms on a Quantum Computer”, SIAM Journal on Computing, 26, 5, 1997, pp. 1484–1509.
2. J. M. Pollard, “A Monte Carlo Method for Factorization”, BIT, 15, 1975, pp. 331–332.
3. R. P. Brent, “An Improved Monte Carlo Factorization Algorithm”, BIT, 20, 1980, pp. 176–184.
4. D. E. Knuth, The Art of Computer Programming II – Seminumerical Algorithms, 3rd Edition, Addison-Wesley, 1998.
5. P. L. Montgomery, “Speeding Pollard’s and Elliptic Curve Methods of Factorization”, Mathematics of Computation, 48, 1987, pp. 243–264.
6. R. P. Brent, “Some Integer Factorization Algorithms using Elliptic Curves”, Australian Computer Science Communications, 8, 1986, pp. 149–163.
7. M. A. Morrison and J. Brillhart, “A Method of Factoring and the Factorization of F7”, Mathematics of Computation, 29, 1975, pp. 183–205.
8. C. Pomerance, “Analysis and Comparison of some Integer Factoring Algorithms”, in H. W. Lenstra, Jr. and R. Tijdeman, eds, Computational Methods in Number Theory, No 154/155, Mathematical Centrum, Amsterdam, 1982, pp. 89–139.
9. H. J. J. te Riele, W. Lioen, and D. Winter, “Factoring with the Quadrtaic Sieve on Large Vector Computers”, Journal of Computational and Applied Mathematics, 27, 1989, pp. 267–278.
10. R. M. Huizing, “An Implementation of the Number Field Sieve”, Experimental Mathematics, 5 3, 1996, pp. 231–253.
11. A. K. Lenstra and H. W. Lenstra, Jr. (editors), The Development of the Number Field Sieve, Lecture Notes in Mathematics 1554, Springer-Verlag, 1993.
12. K. Ireland and M. Rosen, A Classical Introduction to Modern Number Theory, 2nd Edition, Graduate Texts in Mathematics 84, Springer, 1990.
13. P. L. Montgomery, “A Survey of Modern Integer Factorization Algorithms”, CWI Quarterly, 7, 4, 1994, pp. 337–394.
14. L. M. Adleman, “Algorithmic Number Theory – The Complexity Contribution”, Proceedings of the 35th Annual IEEE Symposium on Foundations of Computer Science, IEEE Press, 1994, pp. 88–113.
15. D. Atkins, M. Graff, A. K. Lenstra, and P. C. Leyland, “The Magic Words are Squeamish Ossifrage”, Advances in Cryptology – ASIACRYPT’94, Lecture Notes in Computer Science 917, 1995, pp. 261–277.
16. R. P. Brent, “Primality Testing and Integer Factorization”, Proceedings of Australian Academy of Science Annual General Meeting Symposium on the Role of Mathematics in Science, Canberra, 1991, pp. 14–26.
17. R. P. Brent, “Recent Progress and Prospects for Integer Factorization Algorithms”, Proc. COCOON 2000 (Sydney, July 2000), Lecture Notes in Computer Science 1858, Springer, 2000, pp. 3–22.
18. D. M. Bressound, Factorization and Primality Testing, Springer, 1989.
19. H. Cohen, A Course in Computational Algebraic Number Theory, Graduate Texts in Mathematics 138, Springer-Verlag, 1993.
20. T. H. Cormen, C. E. Ceiserson and R. L. Rivest, Introduction to Algorithms, 3rd Edition, MIT Press, 2009.
21. R. Crandall and C. Pomerance, Prime Numbers – A Computational Perspective, 2nd Edition, Springer-Verlag, 2005.
22. J. D. Dixon, “Factorization and Primality tests”, The American Mathematical Monthly, June–July 1984, pp. 333–352.
23. M. Gardner, “Mathematical Games – A New Kind of Cipher that Would Take Millions of Years to Break”, Scientific American, 237, 2, 1977, pp. 120–124.
24. C. F. Gauss, Disquisitiones Arithmeticae, G. Fleischer, Leipzig, 1801. English translation by A. A. Clarke, Yale University Press, 1966. Revised English translation by W. C. Waterhouse, Springer-Verlag, 1975.
25. A. Granville, “Smooth Numbers: Computational Number Theory and Beyond”, Algorithmic Number Theory. Edited by J. P. Buhler and P. Stevenhagen, Cambridge University Press, 2008, pp. 267–323.
26. T. Kleinjung, et al., “Factorization of a 768-Bit RSA Modulus”, In: T. Rabin (Ed.), CRYPTO 2010, Lecture Notes in Computer Science 6223, Springer, 2010, pp. 333–350.
27. N. Koblitz, A Course in Number Theory and Cryptography, 2nd Edition, Graduate Texts in Mathematics 114, Springer-Verlag, 1994.
28. A. K. Lenstra, “Integer Factoring”, Design, Codes and Cryptography, 19, 2/3, 2000, pp. 101–128.
29. R. A. Mullin, Algebraic Number Theory, 2nd Edition, CRC Press, 2011.
30. C. Pomerance “Integer Factoring”, Cryptology and Computational Number Theory. Edited by C. Pomerance, Proceedings of Symposia in Applied Mathematics, American Mathematical Society, 1990, pp. 27–48.
31. C. Pomerance, “On the Role of Smooth Numbers in Number Theoretic Algorithms”, Proceedings of the Intenational Congress of Mathematicians, Zurich, Switzerland 1994, Birkhauser Verlag, Basel, 1995, pp. 411–422.
32. C. Pomerance, “A Tale of Two Sieves”, Notice of the AMS, 43, 12, 1996, pp. 1473–1485.
33. H. Riesel, Prime Numbers and Computer Methods for Factorization, Birkhäuser, Boston, 1990.
34. V. Shoup, A Computational Introduction to Number Theory and Algebra, Cambridge University Press, 2005.
35. H. C. Williams, “The Influence of Computers in the Development of Number Theory”, Computers & Mathematics with Applications, 8, 2, 1982, pp. 75–93.
36. H. C. Williams, “Factoring on a Computer”, Mathematical Intelligencer, 6, 3, 1984, pp. 29–36.
37. S. Y. Yan, “Computing Prime Factorization and Discrete Logarithms: From Index Calculus to Xedni Calculus”, International Journal of Computer Mathematics, 80, 5, 2003, pp. 573–590.
38. S. Y. Yan, Primality Testing and Integer Factorization in Public-Key Cryptography, Advances in Information Security 11, 2nd Edition, Springer, 2009.
39. S. McMath, Daniel Shanks’ Square Forms Factorization, United States Naval Academy, Annapolis, Maryland, 24 November 2004.
40. J. M. Pollard, “Theorems on Factorization and Primality Testing”, Procedings of Cambridge Philosophy Society, 76, 1974, pp. 521–528.
41. H. C. Williams, “A p + 1 Method of Factoring”, Mathematics of Computation, 39, 1982, pp. 225–234.
42. H. W. Lenstra, Jr., “Factoring Integers with Elliptic Curves”, Annals of Mathematics, 126, 1987, pp. 649–673.
43. C. Pomerance, “The Quadratic Sieve Factoring Algorithm”, Proceedings of Eurocrypt 84, Lecture Notes in Computer Science 209, Springer, 1985, pp. 169–182.
44. C. Pomerance, “Smooth Numbers and the Quadratic Sieve”, Algorithmic Number Theory. Edited by J. P. Buhler and P. Stevenhagen, Cambridge University Press, 2008, pp. 69–81.
45. C. Pomerance, “The Number Field Sieve”, Mathematics of Computation, 1943–1993, Fifty Years of Computational Mathematics. Edited by W. Gautschi, Proceedings of Symposium in Applied Mathematics 48, American Mathematical Society, Providence, 1994, pp. 465–480.
46. P. Stevenhagen, “The Number Field Sieve”, Algorithmic Number Theory. Edited by J.P. Buhler and P. Stevenhagen, Cambridge University Press, 2008, pp. 83–100.
47. R. P. Brent, “Parallel Algorithms for Integer Factorisation”, Number Theory and Cryptography. Edited by J. H. Loxton, London Mathematical Society Lecture Notes i 154, Cambridge University Press, 1990, pp. 26–37.
48. R. P. Brent, “Some Parallel Algorithms for Integer Factorisation”, Proceedings of 5th International Euro-Par Conference(Toulouse, France), Lecture Notes in Computer Science 1685, Springer, 1999, pp. 1–22.
49. A. K. Lenstra and M. S. Manases “Factoring by Electronic Mail”, Advances in Cryptology – EUROCRYPT Ô89. Edited by J. J. Quisquater and J. Vandewalle, Lecture Notes in Computer Science 434, Springer, 1990, pp. 355–371.
50. R. D. Silverman, “Massively Distributed Computing and Factoring Large Integers”, Communications of the ACM, 34, 11, 1991, pp. 95–103.
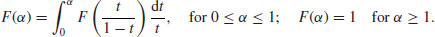
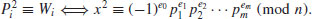
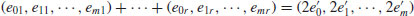
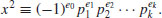
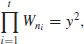
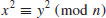
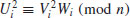
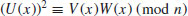
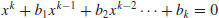

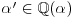 and
and  such that
such that