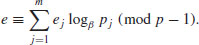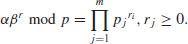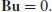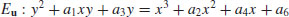5
Discrete Logarithms
The Discrete Logarithm Problem (DLP) and the Elliptic Curve Discrete Logarithm Problem (ECDLP), along with the Integer Factorization Problem (IFP), are the three most important infeasible computational problems in computational number theory and modern cryptography. In this chapter we discuss several popular and widely used modern algorithms for DLP/ECDLP, including:
- Baby-step Giant-step Method for DLP
- Pohlig–Hellman Algorithm for DLP/ECDLP
- The index calculus for DLP
- The xedni calculus for ECDLP.
5.1 Basic Concepts
The Discrete Logarithm Problem (DLP) can be described as follows:
(5.1) 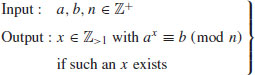
where the modulus n can either be a composite or a prime.
According to Adleman [1], the Russian mathematician Bouniakowsky developed a clever algorithm to solve the congruence 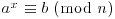 , with the asymptotic complexity
, with the asymptotic complexity 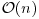 in 1870. Despite its long history, no efficient algorithm has ever emerged for the Discrete Logarithm Problem. It is believed to be hard, a little bit harder than the Integer Factorization Problem (IFP) even in the average case. The best known algorithm for DLP at present, using NFS and due to Gordon [2], requires an expected running time
in 1870. Despite its long history, no efficient algorithm has ever emerged for the Discrete Logarithm Problem. It is believed to be hard, a little bit harder than the Integer Factorization Problem (IFP) even in the average case. The best known algorithm for DLP at present, using NFS and due to Gordon [2], requires an expected running time
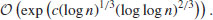
There are essentially three different categories of algorithms in use for computing discrete logarithms:
 Method (an analogue of Pollard’s
Method (an analogue of Pollard’s  Factoring Method) and the
Factoring Method) and the  Method (also known as wild and tame Kangaroos) are in this category.
Method (also known as wild and tame Kangaroos) are in this category.In this chapter, we shall introduce the basic ideas of the algorithms in each of these three categories; more specifically, we shall introduce Shanks’ Baby-step Giant-step algorithm, the Silver–Pohlig–Hellman algorithm, Adleman’s index calculus algorithm, as well as Gordon’s NFS algorithm for computing discrete logarithms. In the last section of this chapter, we shall also deal with algorithms for ECDLP.
Problems for Section 5.1
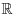 and the discrete logarithms?
and the discrete logarithms?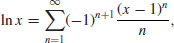
 :
: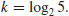
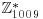 , if there exists:
, if there exists: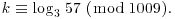
 .
.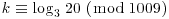 .
.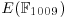 :
: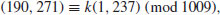
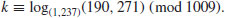

5.2 Baby-Step Giant-Step Method
The Baby-step Giant-step Method is a meet-in-the-middle algorithm for computing the discrete logarithm. It was first studied in 1968 to calculate the class number of an imaginary quadratic field [3]. Let G be a finite cyclic group of order n, a a generator of G and  . The obvious algorithm for computing successive powers of a until b is found takes
. The obvious algorithm for computing successive powers of a until b is found takes  group operations. For example, to compute
group operations. For example, to compute 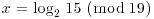 , we compute
, we compute 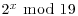 for
for  until
until  for some x is found, that is:
for some x is found, that is:
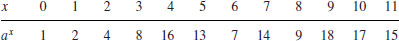
So 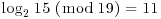 . It is clear that when n is large, the algorithm is inefficient. In this section, we introduce a type of square root algorithm, called the baby-step giant-step algorithm, for taking discrete logarithms, which is better than the above mentioned obvious algorithm. The algorithm works for every finite cyclic group.
. It is clear that when n is large, the algorithm is inefficient. In this section, we introduce a type of square root algorithm, called the baby-step giant-step algorithm, for taking discrete logarithms, which is better than the above mentioned obvious algorithm. The algorithm works for every finite cyclic group.
Let 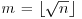 . The baby-step giant-step algorithm is based on the observation that if x = logab, then we can uniquely write x = i + jm, where
. The baby-step giant-step algorithm is based on the observation that if x = logab, then we can uniquely write x = i + jm, where 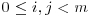 . For example, if
. For example, if 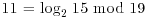 , then a = 2, b = 15, m = 5, so we can write 11 = i + 5j for
, then a = 2, b = 15, m = 5, so we can write 11 = i + 5j for  . Clearly here i = 1 and j = 2 so we have
. Clearly here i = 1 and j = 2 so we have 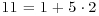 . Similarly, for
. Similarly, for 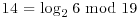 we can write
we can write  , for
, for  we can write
we can write  , etc. The following is a description of the algorithm:
, etc. The following is a description of the algorithm:
Algorithm 5.1 (Shanks’ baby-step giant-step algorithm) This algorithm computes the discrete logarithm x of y to the base a, modulo n, such that  :
:
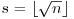 .
.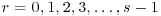 :
:(5.2) 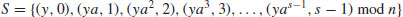
 :
:(5.3) 
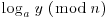 .
.This algorithm requires a table with 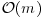 entries (
entries (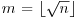 , where n is the modulus). Using a sorting algorithm, we can sort both the lists S and T in
, where n is the modulus). Using a sorting algorithm, we can sort both the lists S and T in 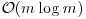 operations. Thus this gives an algorithm for computing discrete logarithms that uses
operations. Thus this gives an algorithm for computing discrete logarithms that uses 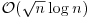 time and space for
time and space for  group elements. Note that Shanks’ idea was originally for computing the order of a group element G in the group G, but here we use his idea to compute discrete logarithms. Note also that although this algorithm works on arbitrary groups, if the order of a group is larger than 1040, it will be infeasible.
group elements. Note that Shanks’ idea was originally for computing the order of a group element G in the group G, but here we use his idea to compute discrete logarithms. Note also that although this algorithm works on arbitrary groups, if the order of a group is larger than 1040, it will be infeasible.
Example 5.1 Suppose we wish to compute the discrete logarithm 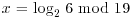 such that
such that 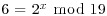 . According to Algorithm 12, we perform the following computations:
. According to Algorithm 12, we perform the following computations:
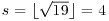 .
.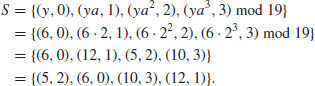
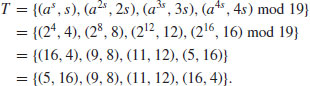
 , or equivalently,
, or equivalently, 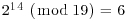 .
.Example 5.2 Suppose now we wish to find the discrete logarithm  , such that
, such that 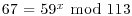 . Again by Algorithm 5.1, we have:
. Again by Algorithm 5.1, we have:
 .
.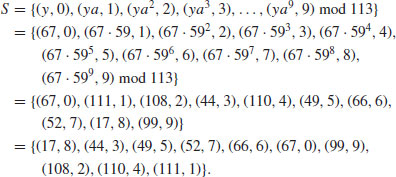
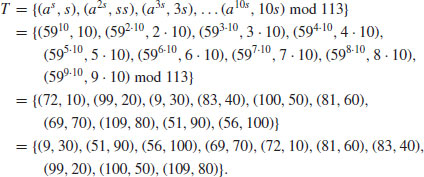
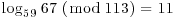 , or equivalently,
, or equivalently, 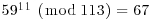 .
.Remark 5.1 Shanks’ baby-step giant-step algorithm is a type of Square Root Method for computing discrete logarithms. In 1978 Pollard [4] also gave two other types of Square Root Methods, namely the 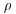 Method (an analogue of Pollard’s
Method (an analogue of Pollard’s  Factoring Method) and the
Factoring Method) and the 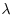 Method (also known as the Wild Kangaroo Method) for computing discrete logarithms. Pollard’s methods are probabilistic but remove the necessity of precomputing the lists S and T, as with Shanks’ Baby-step Giant-step Method. Again, Pollard’s algorithm requires
Method (also known as the Wild Kangaroo Method) for computing discrete logarithms. Pollard’s methods are probabilistic but remove the necessity of precomputing the lists S and T, as with Shanks’ Baby-step Giant-step Method. Again, Pollard’s algorithm requires 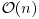 group operations and hence is infeasible if the order of the group G is larger than 1040.
group operations and hence is infeasible if the order of the group G is larger than 1040.
Problems for Section 5.2
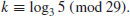
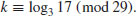
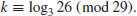
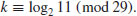
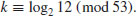
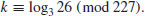
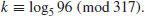
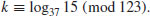

5.3 Pohlig–Hellman Method
In 1978, Pohlig and Hellman [5] proposed an important special algorithm, now widely known as the Silver–Pohlig–Hellman algorithm for computing discrete logarithms over GF(q) with  operations and a comparable amount of storage, where p is the largest prime factor of q−1. Pohlig and Hellman showed that if
operations and a comparable amount of storage, where p is the largest prime factor of q−1. Pohlig and Hellman showed that if
(5.4) 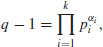
where the pi are distinct primes and the  are natural numbers, and if
are natural numbers, and if  are any real numbers with
are any real numbers with 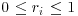 , then logarithms over GF(q) can be computed in
, then logarithms over GF(q) can be computed in

field operations, using
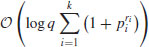
bits of memory, provided that a precomputation requiring
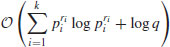
field operations is performed first. This algorithm is very efficient if q is “smooth,” that is, all the prime factors of q−1 are small. We shall give a brief description of the algorithm as follows:
Algorithm 5.2 (Silver–Pohlig–Hellman Algorithm) This algorithm computes the discrete logarithm
(5.5) 
(5.6) 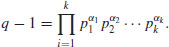
 for a given field:
for a given field:(5.7) 
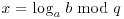 :
: : To compute
: To compute  , we consider the representation of this number to the base pi:
, we consider the representation of this number to the base pi:(5.8) 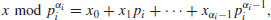
 .
.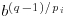 which equals
which equals  for some j, and set x0 = j for which
for some j, and set x0 = j for which(5.9) 
(5.10) 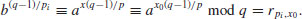
 . If
. If(5.11) 
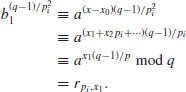
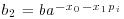 and compute
and compute
 .
. .
.We now give an example of how the above algorithm works:
Example 5.3 Suppose we wish to compute the discrete logarithm 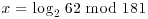 . Now we have a = 2, b = 62 and q = 181 (2 is a generator of
. Now we have a = 2, b = 62 and q = 181 (2 is a generator of 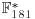 ). We follow the computation steps described in the above algorithm:
). We follow the computation steps described in the above algorithm:
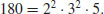
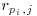 for the given field
for the given field 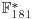 :
:
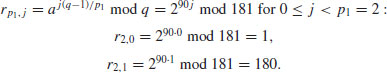
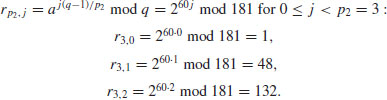
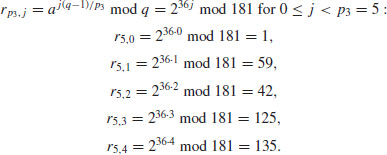
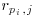 table as follows:
table as follows:
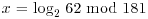 . Here a = 2 and b = 62:
. Here a = 2 and b = 62: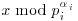 using
using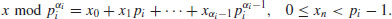
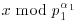 , that is,
, that is, 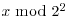 :
: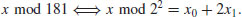
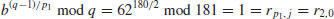
 , then compute
, then compute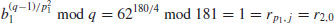

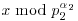 , that is,
, that is, 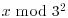 :
: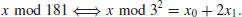
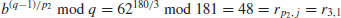
 , then compute
, then compute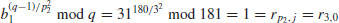
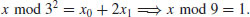
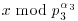 , that is,
, that is,  :
: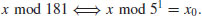
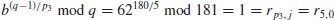

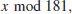
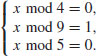
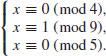
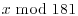 is 100. Hence x = log262 = 100.
is 100. Hence x = log262 = 100.Problems for Section 5.3
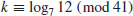
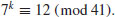
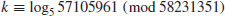
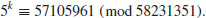
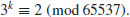
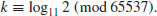
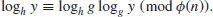
5.4 Index Calculus
In 1979, Adleman [1] proposed a general purpose, subexponential algorithm for computing discrete logarithms, called the index calculus, with the following expected running time:
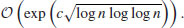
The index calculus is, in fact, a wide range of methods, including CFRAC, QS, and NFS for IFP. In what follows, we discuss a variant of Adleman’s index calculus for DLP in  .
.
Algorithm 5.3 (Index calculus for DLP) This algorithm tries to find an integer k such that
(5.12) 
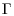 , consisting of the first m prime numbers,
, consisting of the first m prime numbers,(5.13) 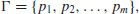
 , the bound of the factor base.
, the bound of the factor base. ) Randomly choose a set of exponent
) Randomly choose a set of exponent  , compute
, compute 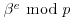 , and factor it as a product of prime powers.
, and factor it as a product of prime powers.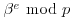 that are smooth with respect to b. That is,
that are smooth with respect to b. That is,(5.14) 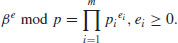
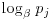 for
for 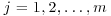 .
.
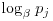 for
for 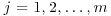 by solving the m modular linear equations with unknown
by solving the m modular linear equations with unknown  .
.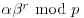 ) Randomly choose exponent
) Randomly choose exponent 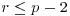 and compute
and compute  .
. over
over 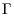 )
)(5.17) 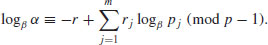
Example 5.4 (Index calculus for DLP) Find
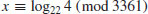
such that
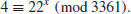
 , consisting of the first 4 prime numbers,
, consisting of the first 4 prime numbers,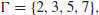
 , the bound of the factor base.
, the bound of the factor base.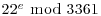 ) Randomly choose a set of exponent
) Randomly choose a set of exponent  , compute
, compute 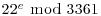 , and factor it as a product of prime powers:
, and factor it as a product of prime powers: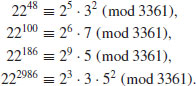
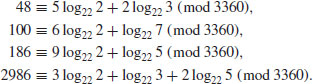

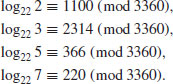
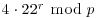 ) Randomly choose exponent
) Randomly choose exponent 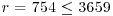 and compute
and compute 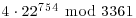 .
. over
over 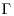 )
)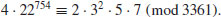
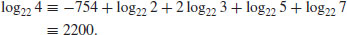
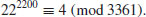
Example 5.5 Find 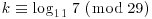 such that
such that  .
.
 .
.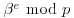 ) Randomly choose e<p, compute and factor
) Randomly choose e<p, compute and factor 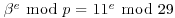 as follows:
as follows: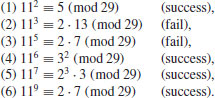
 )
)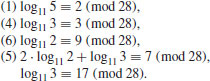
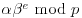 ) Randomly choose e<p, compute and factor
) Randomly choose e<p, compute and factor 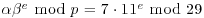 as follows:
as follows: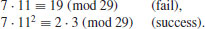
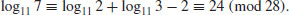
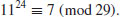
For more than ten years since its invention, Adleman’s method and its variants were the fastest algorithms for computing discrete logarithms. But the situation changed in 1993 Gordon [2] proposed an algorithm for computing discrete logarithms in GF(p). Gordon’s algorithm is based on the Number Field Sieve (NFS) for integer factorization, with the heuristic expected running time
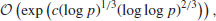
the same as that used in factoring. The algorithm can be briefly described as follows:
Algorithm 5.4 (Gordon’s NFS) This algorithm computes the discrete logarithm x such that 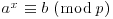 with input a, b, p, where a and b are generators and p is prime:
with input a, b, p, where a and b are generators and p is prime:
 by finding the logarithms of a number of “medium-sized” primes.
by finding the logarithms of a number of “medium-sized” primes.Problems for Section 5.4
 . Use the index calculus method to find the discrete logarithm k:
. Use the index calculus method to find the discrete logarithm k: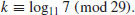
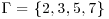 . Use the index calculus method to find the discrete logarithm k:
. Use the index calculus method to find the discrete logarithm k: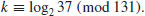
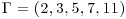 to solve the DLP problem
to solve the DLP problem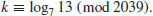

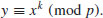
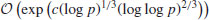
 with p prime, let also
with p prime, let also 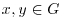 such that
such that 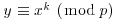 . Use smooth numbers to show that the discrete logarithm
. Use smooth numbers to show that the discrete logarithm  can be computed in expected time
can be computed in expected time  .
.5.5 Elliptic Curve Discrete Logarithms
The Elliptic Curve Discrete Logarithm Problem (ECDLP) is of fundamental importance to ECC (elliptic curve cryptography): Let 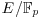 be an elliptic curve over a finite field
be an elliptic curve over a finite field 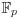 , say, given by a Weierstrass equation
, say, given by a Weierstrass equation
(5.18) 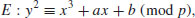
p and q the two points in the elliptic curve group  . Then the ECDLP is to find the integer k (assuming that such an integer k exists)
. Then the ECDLP is to find the integer k (assuming that such an integer k exists)
(5.19) 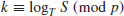
such that
(5.20) 
Formally, the Elliptic Curve Discrete Logarithm Problem (ECDLP) could be defined as follows:
(5.21) 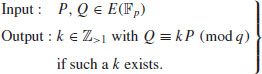
The ECDLP is little bit more difficult than the DLP, on which the elliptic curve digital signature algorithm/elliptic curve digital signature standard (ECDSA/ECDSS) [37] is based on. As ECDLP is the generalization of DLP, which extends, for example, the multiplicative group 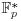 to the elliptic curve group
to the elliptic curve group 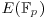 , many methods for DLP, even for IFP, can be extended to ECDLP, for example, the Baby-step Giant-step for DLP, Pollard’s
, many methods for DLP, even for IFP, can be extended to ECDLP, for example, the Baby-step Giant-step for DLP, Pollard’s  and
and  Methods for IFP and DLP; the Silver–Pohlig–Hellman Method for DLP, can also be naturally extended to ECDLP. In what follows, we present an example of solving ECDLP by an analog of the Silver–Pohlig–Hellman Method for elliptic curves over
Methods for IFP and DLP; the Silver–Pohlig–Hellman Method for DLP, can also be naturally extended to ECDLP. In what follows, we present an example of solving ECDLP by an analog of the Silver–Pohlig–Hellman Method for elliptic curves over 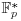 .
.
Example 5.6 Let
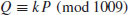
where
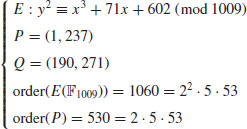
Find k.
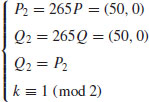
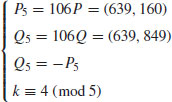
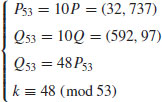
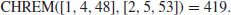
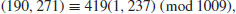
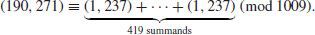
The index calculus for DLP is however generally not suitable for ECDLP as it is not for general groups. In what follows, we introduce a method, called xedni calculus for ECDLP. The xedni calculus was first proposed by Joseph Silverman in [42] and [44], and analyzed in [45]. It is called xedni calculus because it “stands index calculus on its head.” The xedni calculus is a new method that might be used to solve the ECDLP, although it has not yet been tested in practice. It can be described as follows:
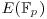 and lift them to points in
and lift them to points in 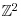 .
.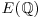 containing the lift points; use Mestre’s Method (in reverse) to make rank
containing the lift points; use Mestre’s Method (in reverse) to make rank 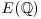 small.
small.Whilst the index calculus works in reverse:
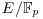 to
to 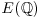 ; use Mestre’s Method to make rank
; use Mestre’s Method to make rank 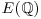 large.
large.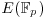 and try to lift them to points in
and try to lift them to points in  .
.A brief description of the xedni algorithm is as follows.
Algorithm 5.5 (Xedni calculus for the ECDLP) Let 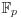 be a finite field with p elements (p prime),
be a finite field with p elements (p prime), 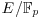 an elliptic curve over
an elliptic curve over 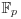 , say, given by
, say, given by
(5.22) 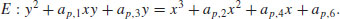
Np the number of points in 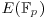 , S and T the two points in
, S and T the two points in 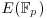 . This algorithm tries to find an integer k
. This algorithm tries to find an integer k
(5.23) 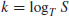
such that
(5.24) 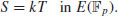
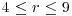 and an integer m which is a product of small primes.
and an integer m which is a product of small primes.(5.25) 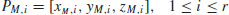
 , the matrix
, the matrix 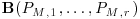 has maximal rank modulo l.
has maximal rank modulo l. such that the points
such that the points 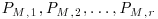 satisfy the congruence:
satisfy the congruence:(5.26) 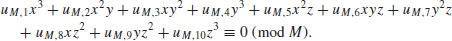
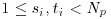 , and for each
, and for each  , compute the point Pp,i = (xp,i, yp,i) defined by
, compute the point Pp,i = (xp,i, yp,i) defined by(5.27) 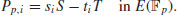
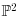 of the form
of the form(5.28) 
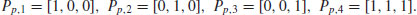
(5.29) 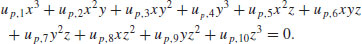
 satisfying
satisfying(5.30) 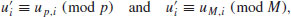
 .
.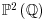 . That is, choose points
. That is, choose points(5.31) 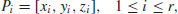
(5.32) 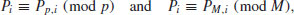
 . In particular, take
. In particular, take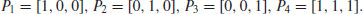
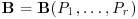 be the matrix of cubic monomials defined earlier. Consider the system of linear equations:
be the matrix of cubic monomials defined earlier. Consider the system of linear equations: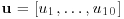 to (5.33) which has the additional property
to (5.33) which has the additional property(5.34) 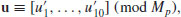
 are the coefficients computed in Step [5]. Let Cu denote the associated cubic curve:
are the coefficients computed in Step [5]. Let Cu denote the associated cubic curve:(5.35) 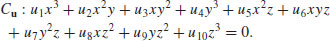
 . Write the resulting equation as
. Write the resulting equation as , and let
, and let 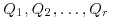 denote the images of
denote the images of  under this change of coordinates (so in particular,
under this change of coordinates (so in particular, 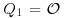 ). Let c4(u), c6(u), and
). Let c4(u), c6(u), and  be the usual quantities in Silverman (2000) associated to the equation (5.36).
be the usual quantities in Silverman (2000) associated to the equation (5.36). are independent. If they are, return to Step [2] or [3]. Otherwise compute a relation of dependence
are independent. If they are, return to Step [2] or [3]. Otherwise compute a relation of dependence(5.37) 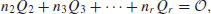
(5.38) 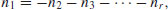
(5.39) 
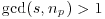 , go to Step [2] or [3]. Otherwise compute an inverse
, go to Step [2] or [3]. Otherwise compute an inverse  . Then
. Then(5.40) 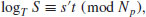
As can be seen, the basic idea in the above algorithm is that we first choose points 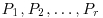 in
in  and lift them to points
and lift them to points 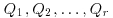 having integer coordinates, then we choose an elliptic curve
having integer coordinates, then we choose an elliptic curve  that goes through the points
that goes through the points  , and finally check if the points
, and finally check if the points  are dependent. If they are, the ECDLP is almost solved. Thus, the goal of the xedni calculus is to find an instance where an elliptic curve has smaller than expected rank. Unfortunately, a set of points
are dependent. If they are, the ECDLP is almost solved. Thus, the goal of the xedni calculus is to find an instance where an elliptic curve has smaller than expected rank. Unfortunately, a set of points 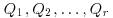 as constructed above will usually be independent. So, it will not work. To make it work, a congruence method, due to Mestre, is used in reverse to produce the lifted curve E having smaller than expected rank.1 Again unfortunately, Mestre’s Method is based on some deep ideas and unproved conjectures in analytic number theory and arithmetic algebraic geometry, it is not possible for us at present to give even a rough estimate of the algorithm’s running time. So, we know virtually nothing about the complexity of the xedni calculus. We also do not know if the xedni calculus will be practically useful; it may be completely useless from a practical point of view. Much needs to be done before we will have a better understanding of the xedni calculus.
as constructed above will usually be independent. So, it will not work. To make it work, a congruence method, due to Mestre, is used in reverse to produce the lifted curve E having smaller than expected rank.1 Again unfortunately, Mestre’s Method is based on some deep ideas and unproved conjectures in analytic number theory and arithmetic algebraic geometry, it is not possible for us at present to give even a rough estimate of the algorithm’s running time. So, we know virtually nothing about the complexity of the xedni calculus. We also do not know if the xedni calculus will be practically useful; it may be completely useless from a practical point of view. Much needs to be done before we will have a better understanding of the xedni calculus.
The index calculus is probabilistic, subexponential-time algorithm applicable for both the Integer Factorization Problem (IFP) and the finite field Discrete Logarithm Problem (DLP). However, there is no known subexponential-time algorithm for the Elliptic Curve Discrete Logarithm Problem (ECDLP); the index calculus will not work for the ECDLP. The xedni calculus, on the other hand, is applicable to ECDLP (it is in fact also applicable to IFP and DLP), but unfortunately its complexity is essentially unknown. From a computability point of view, xedni calculus is applicable to IFP, DLP, and ECDLP, but from a complexity point of view, the xedni calculus may turn out to be useless (i.e., not at all practical). As for quantum algorithms, we now know that IFP, DLP, and ECDLP can all be solved in polynomial-time if a quantum computer is available for use. However, the problem with quantum algorithms is that a practical quantum computer is out of reach in today’s technology. We summarize various algorithms for IFP, DLP, and ECDLP in Table 5.1.
Table 5.1 Algorithms for IFP, DLP, and ECDLP
| IFP | DLP | ECDLP |
| Trial divisions | Baby-step Giant-step | Baby-step Giant-step |
Pollard’s 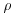 Method Method |
Pollard’s 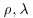 Methods Methods |
Pollard’s 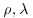 Mmethods Mmethods |
| CFRAC/MPQS | Index calculus | |
| NFS | NFS | |
| Xedni calculus | Xedni calculus | Xedni calculus |
| Quantum algorithms | Quantum algorithms | Quantum algorithms |
Finally, we conclude that we do have algorithms to solve the IFP, DLP, and ECDLP; the only problem is that we do not have an efficient algorithm, nor has any one proved that such an efficient algorithm exists. From a computational complexity point of view, a  -type problem is easy to solve, whereas an
-type problem is easy to solve, whereas an 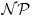 -type problem is easy to verify [7], so the IFP, DLP, and ECDLP are clearly in
-type problem is easy to verify [7], so the IFP, DLP, and ECDLP are clearly in 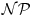 . For example, it might be difficult (indeed, it is difficult at present) to factor a large integer, but it is easy to verify whether or not a given factorization is correct. If
. For example, it might be difficult (indeed, it is difficult at present) to factor a large integer, but it is easy to verify whether or not a given factorization is correct. If 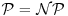 , then two types of the problems are the same, the factorization is difficult only because no one has yet been clever enough to find an easy/efficient algorithm (it may turn out that the integer factorization problem is indeed
, then two types of the problems are the same, the factorization is difficult only because no one has yet been clever enough to find an easy/efficient algorithm (it may turn out that the integer factorization problem is indeed  -hard, regardless of the cleverness of the human beings). Whether or not
-hard, regardless of the cleverness of the human beings). Whether or not 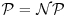 is one of the biggest open problems in both mathematics and computer science, and it is listed in the first of the seven Millennium Prize Problems by the Clay Mathematics Institute in Boston of May 24 2000 [6]. The struggle continues and more research needs to be done before we can say anything about whether or not
is one of the biggest open problems in both mathematics and computer science, and it is listed in the first of the seven Millennium Prize Problems by the Clay Mathematics Institute in Boston of May 24 2000 [6]. The struggle continues and more research needs to be done before we can say anything about whether or not  !
!
Problems for Section 5.5
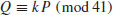
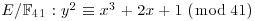 , P = (0, 1) and Q = (30, 40).
, P = (0, 1) and Q = (30, 40). and
and 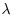 Methods for IFP/DLP can also be extended to ECDLP.
Methods for IFP/DLP can also be extended to ECDLP.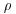 algorithm to solve the ECDLP.
algorithm to solve the ECDLP.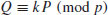
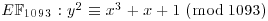 , P = (0, 1) and Q = (413, 959).
, P = (0, 1) and Q = (413, 959).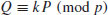
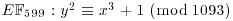 , P = (60, 19) and Q = (277, 239).
, P = (60, 19) and Q = (277, 239).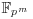 with pm prime power. Give a description and complexity analysis of this algorithm.
with pm prime power. Give a description and complexity analysis of this algorithm.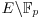 be the elliptic curve E over
be the elliptic curve E over  with p prime, where E is defined by
with p prime, where E is defined by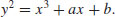
 with
with  are two points on E. Find the addition formula for computing P + Q.
are two points on E. Find the addition formula for computing P + Q.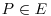 with
with  . Find the addition formula for computing 2P.
. Find the addition formula for computing 2P. be as follows:
be as follows: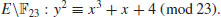
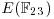 , including the point at infinity, on the E.
, including the point at infinity, on the E. defined above, find P + Q and 2P.
defined above, find P + Q and 2P. . Find
. Find  , the discrete logarithm over
, the discrete logarithm over 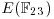 .
.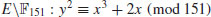
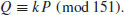
 , the discrete logarithm over
, the discrete logarithm over 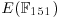 .
.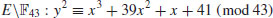
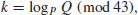
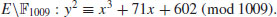

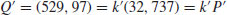
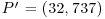 .
. or over
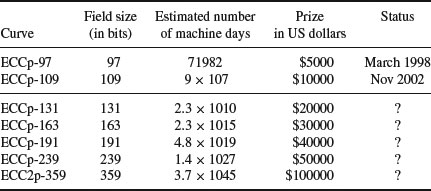
or over 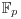 with p prime (see Table 5.2 and Table 5.3). Also there are three levels of difficulty associated with the curves: Exercise level (with bits less than 109), rather easy level (with bits 109–131), and very hard level (with bits 163–359). Readers who are interested in solving real-world ECDLP problems are suggested to try to solve the problems listed in Table 5.2 and Table 5.3, particularly those with the question marks “?” as they are still open.
with p prime (see Table 5.2 and Table 5.3). Also there are three levels of difficulty associated with the curves: Exercise level (with bits less than 109), rather easy level (with bits 109–131), and very hard level (with bits 163–359). Readers who are interested in solving real-world ECDLP problems are suggested to try to solve the problems listed in Table 5.2 and Table 5.3, particularly those with the question marks “?” as they are still open.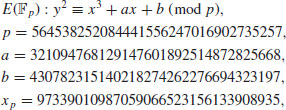
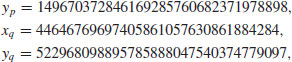
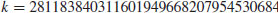
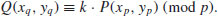
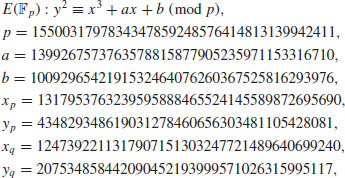
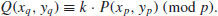
Table 5.2 Elliptic curves over 
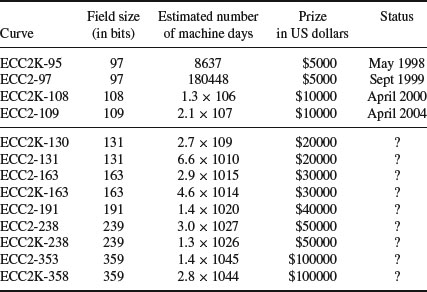
Table 5.3 Elliptic curves over 
5.6 Bibliographic Notes and Further Reading
In this chapter, we presented some important modern algorithms for the Discrete Logarithm Problem (DLP) and the Elliptic Curve Discrete Logarithm Problem (ECDLP).
For general references on DLP and methods for solving DLP, it is suggested that readers consult: [8–26].
The Baby-step and Giant-step Method for DLP was originally proposed by Shanks in 1971 [3]. Pohlig–Hellman method of DLP was proposed in [5]. The  and
and 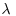 Methods were proposed by Pollard in [4].
Methods were proposed by Pollard in [4].
The currently most powerful method, the index calculus, for DLP is discussed in many references such as [1,2, 27,28]. Generally speaking, the index calculus belongs to a wide range of methods, such as the Continued FRACtion Method (CFRAC), Quadratic Sieve (QS), and Number Field Sieve (NFS). As far as Number Field Sieve is concerned, there is an analog method, called Function Field Sieve, based on the algebraic function field which is just an analog of the number field. FFS, just the as NFS, can be used for solving both IFP and DLP. For more information on FFS, see [29,30].
The ECDLP and methods for ECDLP are discussed in, for example, [31–43]. In particular, the xedni calculus for ECDLP was proposed in [44] and analyzed in [45].
References
1. L. M. Adleman, “A Subexponential Algorithmic for the Discrete Logarithm Problem with Applications to Cryptography”, Proceedings of the 20th Annual IEEE Symposium on Foundations of Computer Science, IEEE Press, 1979, pp. 55–60.
2. D. M. Gordon, “Discrete Logarithms in GF(p) using the Number Field Sieve”, SIAM Journal on Discrete Mathematics, 6, 1, 1993, pp. 124–138.
3. D. Shanks. “Class Number, A theory of Factorization and Genera”. In: Proceedings of Symposium of Pure Mathematics 20, AMS, Providence, R.I., 1971, pp. 415–440.
4. J. M. Pollard, “Monte Carlo Methods for Index Computation 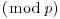 ”, Mathematics of Computation, 32, 1980, pp. 918–924.
”, Mathematics of Computation, 32, 1980, pp. 918–924.
5. S. C. Pohlig and M. Hellman, “An Improved Algorithm for Computing Logarithms over GF(p) and its Cryptographic Significance”, IEEE Transactions on Information Theory, 24, 1978, pp. 106–110.
6. S. Cook, “The P versus NP Problem”, The Millennium Prize Problems. Edited by J. Carlson, A. Jaffe, and A. Wiles, Clay Mathematical Institute and American Mathematical Institute, 2006, pp. 87–104.
7. M. R. Gary and D. S. Johnson, Computers and Intractability – A Guide to the Theory of NP-Completeness, W. H. Freeman and Company, 1979.
8. H. Cohen, A Course in Computational Algebraic Number Theory, Graduate Texts in Mathematics 138, Springer-Verlag, 1993.
9. H. Cohen and G. Frey, Handbook of Elliptic and Hyperelliptic Curve Cryptography, CRC Press, 2006.
10. R. Crandall and C. Pomerance, Prime Numbers – A Computational Perspective, 2nd Edition, Springer-Verlag, 2005.
11. T. Hayashi, N. Shinohara, L. Wang, et al., “Solving a 676-Bit Discrete Logarithm Problem in GF(36n)”, Public Key Cryptography – PKC 2010, Lecture Notes in Computer Science 6056, Springer, 2010, pp. 351–367.
12. T. ElGamal, “A Public Key Cryptosystem and a Signature Scheme based on Discrete Logarithms”, IEEE Transactions on Information Theory, 31, 1985, pp. 496–472.
13. N. Koblitz, A Course in Number Theory and Cryptography, 2nd Edition, Graduate Texts in Mathematics 114, Springer-Verlag, 1994.
14. N. Koblitz, Algebraic Aspects of Cryptography, Algorithms and Computation in Mathematics 3, Springer, 1998.
15. K. S. McCurley, “The Discrete Logarithm Problem”, Cryptology and Computational Number Theory. Edited by C. Pomerance, Proceedings of Symposia in Applied Mathematics 42, American Mathematics Society, 1990, pp. 49–74.
16. K. S. McCurley, “Odds and Ends from Cryptology and Computational Number Theory”, Cryptology and Computational Number Theory. Edited by C. Pomerance, Proceedings of Symposia in Applied Mathematics 42, American Mathematics Society, 1990, pp. 49–74.
17. A. Menezes, P. C. van Oorschot, and S. A. Vanstone, Handbook of Applied Cryptosystems, CRC Press, 1996.
18. A. M. Odlyzko, “Discrete Logarithms in Finite Fields and their Cryptographic Significance”, Advances in Cryptography, EUROCRYPT ’84, Proceedings, Lecture Notes in Computer Science 209, Springer, 1984, pp. 225–314.
19. A. M. Odlyzko, “Discrete Logarithms: the Past and the future”, Design, Codes, and Cryptography, 19, (2000), pp. 129–145.
20. C. Pomerance, “Elementary Thoughts on Discrete Logarithms”, Algorithmic Number Theory. Edited by J. P. Buhler and P. Stevenhagen, Cambridge University Press, 2008, pp. 385–395.
21. H. Riesel, Prime Numbers and Computer Methods for Factorization, Birkhäuser, Boston, 1990.
22. O. Schirokauere, “The Impact of the Number Field Sieve on the Discrete Logarithm Problem in Finite Fields”, Algorithmic Number Theory. Edited by J. P. Buhler and P. Stevenhagen, Cambridge University Press, 2008, pp. 421–446.
23. V. Shoup, A Computational Introduction to Number Theory and Algebra, Cambridge University Press, 2005.
24. S. S. Wagstaff, Jr., Cryptanalysis of Number Theoretic Ciphers, Chapman & Hall/CRC Press, 2002.
25. S. Y. Yan, “Computing Prime Factorization and Discrete Logarithms: From Index Calculus to Xedni Calculus”, International Journal of Computer Mathematics, 80, 5, 2003, pp. 573–590.
26. S. Y. Yan, Primality Testing and Integer Factorization in Public-Key Cryptography, Advances in Information Security 11, 2nd Edition, Springer, 2009.
27. D. M. Gordon and K. S. McCurley, “Massively Parallel Computation of Discrete Logarithms”, Advances in Cryptology – Crypto ’92, Lecture Notes in Computer Science 740, Springer, 1992, pp. 312–323.
28. O. Schirokauer, D. Weber and T. Denny, “Discrete Logarithms: The Effectiveness of the Index Calculus Method”, Algorithmic Number Theory (ANTS-II), Lecture Notes in Computer Science 1122, Springer, 1996, pp. 337–362.
29. L. M. Adleman, “The Function Field Sieve”, Algorithmic Number Theory (ANTS-I), Lecture Notes in Computer Science 877, Springer, 1994, pp. 108–121.
30. L. M. Adleman, “Function Field Sieve Method for Discrete Logarithms over Finite Fields”, AInformation and Computation, 151, 1999, pp. 5–16.
31. I. Blake, G. Seroussi, and N. Smart, Elliptic Curves in Cryptography, Cambridge University Press, 1999.
32. I. Blake, G. Seroussi, and N. Smart, Advances in Elliptic Curves Cryptography, Cambridge University Press, 2005.
33. H. Cohen and G. Frey, Handbook of Elliptic and Hyperelliptic Curve Cryptography, CRC Press, 2006.
34. R. Crandall and C. Pomerance, Prime Numbers – A Computational Perspective, 2nd Edition, Springer, 2005.
35. D. Hankerson, A. J. Menezes, and S. Vanstone, Guide to Elliptic Curve Cryptography, Springer, 2004.
36. J. Hoffstein, J. Pipher, and J. H. Silverman, An Introduction to Mathematical Cryptography, Springer, 2008.
37. D. Johnson, A. Menezes, and S. Vanstone, “The Elliptic Curve Digital Signatures Algorithm (ECDSA)”, International Journal of Information Security, 1, 1, 2001, pp. 36–63.
38. N. Koblitz, A Course in Number Theory and Cryptography, 2nd Edition, Graduate Texts in Mathematics 114, Springer, 1994.
39. N. Koblitz, Algebraic Aspects of Cryptography, Algorithms and Computation in Mathematics 3, Springer, 1998.
40. A. Menezes, T. Okamoto, and S. A. Vanstone, “Reducing Elliptic Curve Logarithms in a Finite Field”, IEEE Transactions on Information Theory, 39, 5, 1993, pp. 1639–1646.
41. J. H. Silverman, The Arithmetic of Elliptic Curves, Graduate Texts in Mathematics 106, 2nd Edition, Springer, 2010.
42. J. H. Silverman and J. Suzuki, “Elliptic Curve Discrete Logarithms and the Index Calculus”, Advances in Cryptology – ASIACRYPT ’98, Lecture Notes in Computer Science 1514, Springer, 1998, pp. 110–125.
43. L. Washington, Elliptic Curves: Number Theory and Cryptography, 2nd Edition, Chapman & Hall/CRC, 2008.
44. J. H. Silverman, “The Xedni Calculus and the Elliptic Curve Discrete Logarithm Problem”, Designs, Codes and Cryptography, 20, 2000, pp. 5-40.
45. M. J. Jacobson, N. Koblitz, J. H. Silverman, et al. “Analysis of the Xedni Calculus Attack”, Designs, Codes and Cryptography, 20, 2000, pp. 41-64.
1 Mestre’s original method is to produce elliptic curves of large rank.