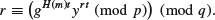8
Discrete Logarithm Based Cryptography
In this chapter, we shall introduce some of the well-known and widely used public-key cryptographic systems and protocols whose security relies on the infeasibility of the DLP; these include:
- The Diffie–Hellman–Merkle key-exchange protocol
- The ElGamal cryptographic system
- The Massey–Omura cryptographic system
- The US government’s Digital Signature Standard.
8.1 Diffie–Hellman–Merkle Key-Exchange Protocol
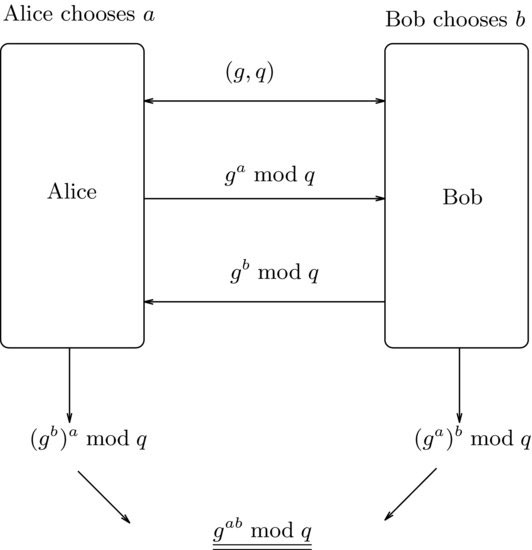
In 1976 Diffie and Hellman [1] proposed for the first time the concept and idea of public-key cryptography, and the first public-key system based on the infeasible Discrete Logarithm Problem (DLP). Their system is not a public-key cryptographic system, but a public-key distribution system based on Merkle’s seminal work in 1978 [2] (Figure 8.1 shows the DHM crypto years in the 1970s). Such a public-key distribution scheme does not send secret messages directly, but rather allows the two parties to agree on a common private key over public networks to be used later in exchanging messages through conventional secret-key cryptography. Thus, the Diffie–Hellman–Merkle scheme has the nice property that a very fast encryption scheme such as DES or AES can be used for actual encryption (just using the agreed key), yet it still enjoys one of the main advantages of public-key cryptography. The Diffie–Hellman–Merkle key-exchange protocol works in the following way (see also Figure 8.2):
Figure 8.1 Merkle, Hellman and Diffie (Courtesy of Prof Hellman)

Figure 8.2 DHM key-exchange protocol
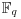 ),
), and sends
and sends 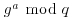 to Bob,
to Bob, and sends
and sends 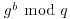 to Alice,
to Alice,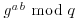 and use this as a private key for future communications.
and use this as a private key for future communications.Clearly, an eavesdropper has g, q, 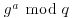 , and
, and 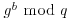 , so if he can take discrete logarithms, he can calculate
, so if he can take discrete logarithms, he can calculate 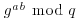 and understand the communications. That is, if the eavesdropper can use his knowledge of g, q,
and understand the communications. That is, if the eavesdropper can use his knowledge of g, q, 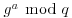 , and
, and 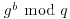 to recover the integer a, then he can easily break the Diffie–Hellman–Merkle system. So, the security of the Diffie–Hellman–Merkle system is based on the following assumption:
to recover the integer a, then he can easily break the Diffie–Hellman–Merkle system. So, the security of the Diffie–Hellman–Merkle system is based on the following assumption:
Diffie–Hellman–Merkle assumption : It is computationally infeasible to compute 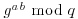 from
from 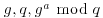 and
and 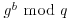 . That is,
. That is,
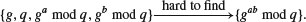
The Diffie–Hellman–Merkle assumption, in turn, depends on the following Discrete Logarithm Problem assumption, that is,
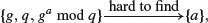
or
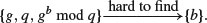
In theory, there could be a way to use knowledge of 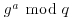 and
and 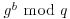 to find
to find 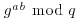 . But at present, we simply cannot imagine a way to go from
. But at present, we simply cannot imagine a way to go from 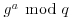 and
and 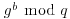 to
to 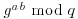 without essentially solving the following Discrete Logarithm Problem:
without essentially solving the following Discrete Logarithm Problem:
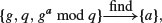
or
If either a or b can be found efficiently, then DHM can be broken easily, since
or
Example 8.1 The following DHM challenge problem was proposed in [3].
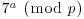 , and sends the result to Bob, keeping a secret.
, and sends the result to Bob, keeping a secret.
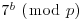 , and sends the result to Alice, keeping b secret.
, and sends the result to Alice, keeping b secret.
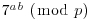 .
.McCurley offered a prize of $100 in 1989 to the first person or group to find the private key constructed from the above communication.
Example 8.2 McCurley’s 129-digit discrete logarithm challenge was actually solved on January 25 1998 using the NFS method, by two German computer scientists, Weber at the Institut für Techno-und Wirtschaftsmathematik in Kaiserslautern and Denny at the Debis IT Security Services in Bonn [4]. Their solution to McCurley’s DLP problem is as follows.

As we have already mentioned earlier, the Diffie–Hellman–Merkle scheme is not intended to be used for actual secure communications, but for key-exchanges. There are, however, several other cryptosystems based on discrete logarithms that can be used for secure message transmissions.
Problems for Section 8.1
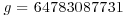 , , |
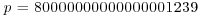 . . |
Then each of them chooses at random a secret random number
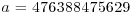 by Alice, by Alice, |
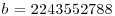 by Bob. by Bob. |
You are asked to compute
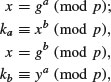
and then to check if
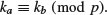

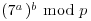 .
.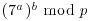 agrees with Weber and Denny’s result, that is, check if
agrees with Weber and Denny’s result, that is, check if 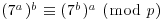 .
.
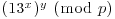 .
.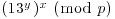 .
.8.2 ElGamal Cryptography
In 1985, ElGamal [5], then a PhD student of Hellman at Stanford, proposed the first DLP-based public-key cryptosystem, since the plaintext M can be recovered by taking the following discrete logarithms
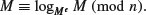
The ElGamal cryptosystem can be described as follows (see also Figure 8.3).
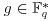 are made public.
are made public.(8.1) 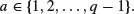
This a is the private decryption key. The public encryption key is  .
.
 and sends Alice the following pair of elements of
and sends Alice the following pair of elements of 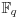 :
:
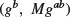
where M is the message.
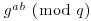 and dividing this result into the second element. That is,
and dividing this result into the second element. That is,
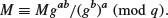
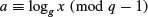
such that
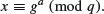
Figure 8.3 ElGamal Cryptography
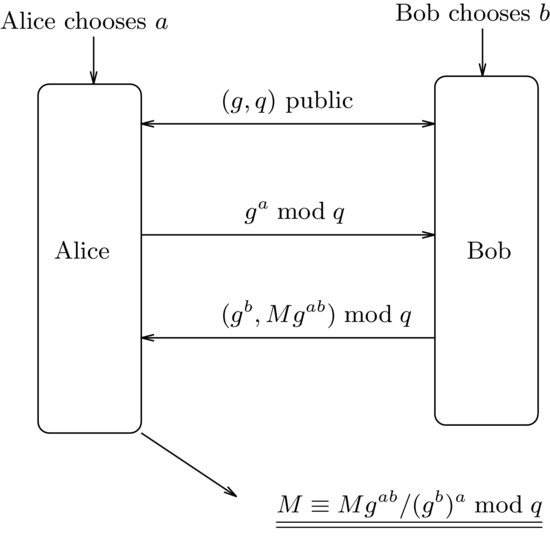
Figure 8.4 The Massey-Omura Cryptography

Remark 8.1 Anyone who can solve the discrete logarithm problem in 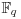 breaks the cryptosystem by finding the secret decryption key a from the public encryption key ga. In theory, there could be a way to use knowledge of ga and gb to find gab and hence break the cipher without solving the discrete logarithm problem. But as we have already seen in the Diffie–Hellman–Merkle scheme, there is no known way to go from ga and gb to gab without essentially solving the discrete logarithm problem. So, the ElGamal cryptosystem is equivalent to the Diffie–Hellman–Merkle key-exchange system.
breaks the cryptosystem by finding the secret decryption key a from the public encryption key ga. In theory, there could be a way to use knowledge of ga and gb to find gab and hence break the cipher without solving the discrete logarithm problem. But as we have already seen in the Diffie–Hellman–Merkle scheme, there is no known way to go from ga and gb to gab without essentially solving the discrete logarithm problem. So, the ElGamal cryptosystem is equivalent to the Diffie–Hellman–Merkle key-exchange system.
Problems for Section 8.2

where 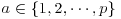 must be kept as a secret. Now Bob can send Alice an encrypted message C = (gb, Mgab) to Alice by using her public-key information, where
must be kept as a secret. Now Bob can send Alice an encrypted message C = (gb, Mgab) to Alice by using her public-key information, where

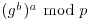 .
.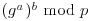 .
.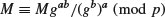
or
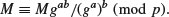
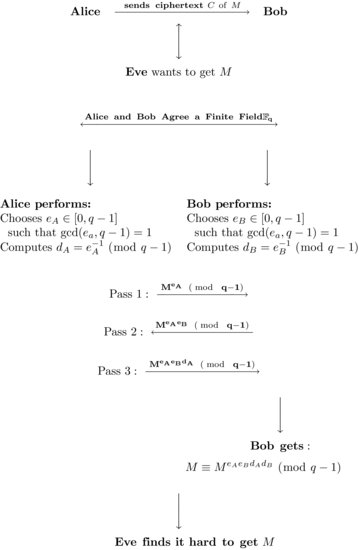
8.3 Massey–Omura Cryptography
The Massey–Omura cryptosystem is another popular public-key cryptosystem based on discrete logarithms over the finite field  , with p = pr prime power. It was proposed by James Massey and Jim K. Omura in 1982 [6] as a possible improvement over Shamir’s original three-pass cryptographic protocol was developed around 1980, in which the sender and the receiver do not exchange any keys, however, the protocol does require the sender and receiver to have two private keys for encrypting and decrypting messages. Thus, the Massey–Omura cryptosystem works in the following steps (see Figure 8.4):
, with p = pr prime power. It was proposed by James Massey and Jim K. Omura in 1982 [6] as a possible improvement over Shamir’s original three-pass cryptographic protocol was developed around 1980, in which the sender and the receiver do not exchange any keys, however, the protocol does require the sender and receiver to have two private keys for encrypting and decrypting messages. Thus, the Massey–Omura cryptosystem works in the following steps (see Figure 8.4):
 with q a prime power.
with q a prime power.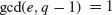 , and computes
, and computes 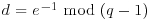 by using the extended Euclidean algorithm. At the end of this step, Alice gets (eA, dA) and Bob gets (eB, dB).
by using the extended Euclidean algorithm. At the end of this step, Alice gets (eA, dA) and Bob gets (eB, dB).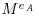 to Bob,
to Bob,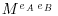 back to Alice (note that at this point, Bob cannot read Alice’s message M),
back to Alice (note that at this point, Bob cannot read Alice’s message M),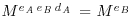 to Bob,
to Bob,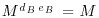 , and hence recovers Alice’s original message M.
, and hence recovers Alice’s original message M.The Massey–Omura cryptosystem is also be described in detail in Figure 8.5 (suppose Alice wants to send Bob a secret message M, with Eve, the attacker in the middle).
Example 8.3 Let

Then


Problems for Section 8.3
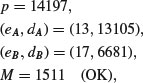
Find
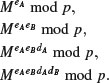
and check if 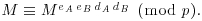

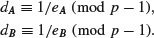
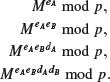
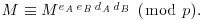
Figure 8.5 The Massey–Omura three-pass cryptographic protocol
8.4 DLP-Based Digital Signatures
In this section, we shall introduce a very influential signature scheme based on ElGamal’s cryptosystem; the security of such a signature scheme depends on the intractability of discrete logarithms over a finite field.
Algorithm 8.1 (ElGamal signature scheme) This algorithm tries to generate a digital signature S = (a, b) for message M. Suppose that Alice wishes to send a signed message to Bob.
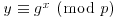 .
.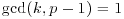 .
.(8.2) 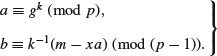
(8.3) 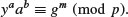
In August 1991, the US Government’s National Institute of Standards and Technology (NIST) proposed an algorithm for digital signatures. The algorithm is known as DSA, for digital signature algorithm. The DSA has become the US Federal Information Processing Standard 186 (FIPS 186). It is called the Digital Signature Standard (DSS) [13], and is the first digital signature scheme recognized by any government. The role of DSA/DSS is expected to be analogous to that of the Data Encryption Standard (DES). The DSA/DSS is similar to a signature scheme proposed by Schnorr; it is also similar to a signature scheme of ElGamal. The DSA is intended for use in electronic mail, electronic funds transfer, electronic data interchange, software distribution, data storage, and other applications which require data integrity assurance and data authentication. The DSA/DSS consists of two main processes:
A one-way hash function is used in the signature generation process to obtain a condensed version of data, called a message digest. The message digest is then signed. The digital signature is sent to the intended receiver along with the signed data (often called the message). The receiver of the message and the signature verifies the signature by using the sender’s public key. The same hash function must also be used in the verification process. In what follows, we shall give the formal specifications of the DSA/DSS.
Algorithm 8.2 (Digital signature algorithm, DSA) This is a variation of the ElGamal signature scheme. It generates a signature S = (r, s) for the message M.
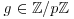 whose multiplicative order is q, that is,
whose multiplicative order is q, that is, 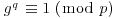 .
.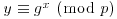 . Clearly, the secret x is the discrete logarithm of y, modulo p, to the base g.
. Clearly, the secret x is the discrete logarithm of y, modulo p, to the base g.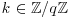 and computing
and computing
(8.4) 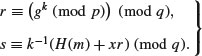
(8.5) 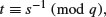
and then accepts the signature as valid if the following congruence holds:
If the congruence (8.6) does not hold, then the message either may have been incorrectly signed, or may have been signed by an impostor. In this case, the message is considered to be invalid.
There are, however, many responses solicited by the (US) Association of Computing Machinery (ACM), positive and negative, to the NIST’s DSA. Some positive aspects of the DSA include:
Whilst some negative aspects of the DSA include:
Nevertheless, the DSA is the only publicly known government digital signature standard.
Problems for Section 8.4
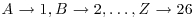 .)
.)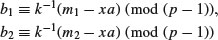
where
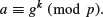
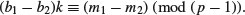
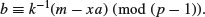
Propose three such variations.
8.5 Bibliographic Notes and Further Reading
This chapter discussed some of the most important and widely used public-key cryptographic systems and digital signatures, whose security relies on the infeasibility of the Discrete Logarithm Problem (DLP). The first public-key system, namely, the key-exchange scheme, was first proposed by Diffie and Hellman in 1976 in [1], based on an idea of Merkle’s [2] (although published later). The first Discrete Logarithm Problem based cryptographic system and digital signature scheme were proposed by ElGamal in 1985 [5]. For general references on Discrete Logarithm Problem based cryptographic systems and digital signature systems, it is suggested that readers consult [8–42].
References
1. W. Diffie and E. Hellman, “New Directions in Cryptography”, IEEE Transactions on Information Theory, 22, 5, 1976, pp. 644–654.
2. R. C. Merkle, “Secure Communications over Insecure Channels” Communications of the ACM, 21, 1978, pp. 294–299. (Submitted in 1975.)
3. K. S. McCurley, “The Discrete Logarithm Problem”, Cryptology and Computational Number Theory. Edited by C. Pomerance, Proceedings of Symposia in Applied Mathematics 42, American Mathematics Society, 1990, pp. 49–74.
4. D. Weber and T. F. Denny, “The Solution of McCurley’s Discrete Log Challenge”, Advances in Cryptology - CRYPTO ’98, Lecture Notes in Computer Science 1462, 1998, pp. 458–471.
5. T. ElGamal, “A Public Key Cryptosystem and a Signature Scheme based on Discrete Logarithms”, IEEE Transactions on Information Theory, 31, 1985, pp. 496–472.
6. J. L. Massey and J.K. Omura, Method and Apparatus for Maintainining the Privacy of Digital Message Conveyed by Public Transmission, US Patent No 4677600, 28 Jan 1986.
7. R. E. Lewand, Cryptological Mathematics, The Mathematical Association of America, 2000.
8. L. M. Adleman, “A Subexponential Algorithmic for the Discrete Logarithm Problem with Applications to Cryptography”, Proceedings of the 20th Annual IEEE Symposium on Foundations of Computer Science, IEEE Press, 1979, pp. 55–60.
9. T. H. Barr, Invitation to Cryptology, Prentics-Hall, 2002.
10. F. L. Bauer, Decrypted Secrets – Methods and Maxims of Cryptology, 3rd Edition, Springer-Verlag, 2002.
11. D.Bishop, Introduction to Cryptography with Java Applets, Jones and Bartlett, 2003.
12. J. A. Buchmann, Introduction to Cryptography, 2nd Edition, Springer, 2004.
13. Communications of the ACM, “The Digital Signature Standard Proposed by NIST and Responses to NIST’s Proposal”, Communications of the ACM, 35, 7, 1992, pp. 36–54.
14. T. H. Cormen, C. E. Ceiserson and R. L. Rivest, Introduction to Algorithms, 3rd Edition, MIT Press, 2009.
15. A. J. Elbirt, Understanding and Applying Cryptography and Data Security. CRC Press, 2009.
16. B. A. Forouzan, Cryptography and Network Security, McGraw-Hill, 2008.
17. J. Hoffstein, J. Pipher, and J. H. Silverman, An Introduction to Mathematical Cryptography, Springer-Verlag, 2008.
18. J. Katz and Y. Lindell, Introduction to Modern Cryptography. CRC Press, 2008.
19. N. Koblitz, A Course in Number Theory and Cryptography, 2nd Edition, Graduate Texts in Mathematics 114, Springer-Verlag, 1994.
20. N. Koblitz, Algebraic Aspects of Cryptography, Algorithms and Computation in Mathematics 3, Springer, 1998.
21. N. Koblitz, “A Survey of Number Theory and Cryptography”, Number Theory. Edited by P. Bambah, V. C. Dumir, and R. J. Hans-Gill, Birkhäser, 2000, pp. 217–239.
22. N. Koblitz, “Cryptography”, in: Mathematics Unlimited – 2001 and Beyond, Edited by B. Enguist and W. Schmid, Springer, 2001, pp. 749–769.
23. W. Mao, Modern Cryptography, Prentice-Hall, 2004.
24. A. Menezes, P. C. van Oorschot, and S. A. Vanstone, Handbook of Applied Cryptosystems, CRC Press, 1996.
25. R. A. Mollin, An Introduction to Cryptography, 2nd Edition, Chapman & Hall/CRC Press, 2006.
26. A. M. Odlyzko, “Discrete Logarithms in Finite Fields and their Cryptographic Significance”, Advances in Cryptography, EUROCRYPT ’84, Proceedings, Lecture Notes in Computer Science 209, Springer, 1984, pp. 225–314.
27. S. C. Pohlig and M. Hellman, “An Improved Algorithm for Computing Logarithms over GF(p) and its Cryptographic Significance”, IEEE Transactions on Information Theory, 24, 1978, pp. 106–110.
28. M. Rabin, “Digitalized Signatures and Public-Key Functions as Intractable as Factorization”, Technical Report MIT/LCS/TR-212, MIT Laboratory for Computer Science, 1979.
29. J. Rothe, Complexity Theory and Cryptography, Springer, 2005.
30. B. Schneier, Applied Cryptography: Protocols, Algorithms, and Source Code in C, 2nd Edition, John Wiley & Sons, 1996.
31. S. Singh, The Code Book: The Science of Secrecy from Ancient Egypt to Quantum Cryptography, Fourth Estate, London, 1999.
32. S. Singh, The Science of Secrecy – The History of Codes and Codebreaking, Fourth Estate, London, 2000.
33. N. Smart, Cryptography: An Introduction, McGraw-Hill, 2003.
34. M. Stamp and R. M. Low, Applied Cryptanalysis, Wiley, 2007.
35. A. Stanoyevitch, Introduction to Cryptography, CRC Press, 2011.
36. D. R. Stinson, Cryptography: Theory and Practice, 3rd Edition, Chapman & Hall/CRC Press, 2006.
37. C.Swenson Modern Cryptanalysis, Wiley, 2008.
38. H. C. A. van Tilborg, Fundamentals of Cryptography, Kluwer Academic Publishers, 1999.
39. W. Trappe and L. Washington, Introduction to Cryptography with Coding Theory, 2nd Edition, Prentice-Hall, 2006.
40. S. S. Wagstaff, Jr., Cryptanalysis of Number Theoretic Ciphers, Chapman & Hall/CRC Press, 2002.
41. S. Y. Yan, Number Theory for Computing, 2nd Edition, Springer-Verlag, 2002.
42. S. Y. Yan, Primality Testing and Integer Factorization in Public-Key Cryptography, Advances in Information Security 11, 2nd Edition, Springer, 2009.