11

Quantum Resistant Cryptography

Once a practical quantum computer with several thousand quantum bits can be built, all the IFP-, DLP-, and ECDLP-based cryptographic systems and protocols can be broken in polynomial-time and hence are no more secure. However, there are still many problems that cannot be solved by a quantum computer in polynomial-time. These problems form a class of quantum-computing (or quantum-attack) resistant problems, and the cryptographic systems and protocols based on these problems will be quantum-computing resistant. In this chapter, we shall introduce:

• A coding-based quantum-computing resistant cryptographic system
• A lattice-based quantum-computing resistant cryptographic system
• A cryptographic protocol based on the idea of quantum mechanics
• DNA Based Biological Cryptography.

11.1 Coding-Based Cryptography

We first introduce the most famous code-based cryptosystem, the McEliece system, invented by McEliece in 1978 [1]. One of the most important features of the McEliece system is that it has resisted cryptanalysis to date; it is even quantum computer resistant. The idea of the McEliece system is based on coding theory and its security is based on the fact that decoding an arbitrary linear code is 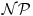-complete.

Algorithm 11.1 (McEliece’s coding-based cryptography) Suppose Bob wishes to send an encrypted message to Alice, using Alice’s public key. Alice generates her public key and the corresponding private key. Bob uses her public key to encrypt his message and sends it to Alice, Alice uses her own private key to decrypt Bob’s message.

1. Key generation: Alice performs:

[1-1] Choose integers k, n, t as common system parameters.

[1-2] Choose a k × n generator matrix G for a binary (n, k)-linear code which can correct t errors and for which an efficient decoding algorithm exists.

[1-3] Select a random k × k binary nonsingular matrix S.

[1-4] Select a random k × k permutation matrix P.

[1-5] Compute the k × n matrix .

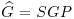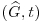[1-6] Now is Alice’s public key whereas (S, G, P) is Alice’s private key.

2. Encryption: Bob uses Alice’s public key to encrypt his message to Alice. Bob performs:

[2-1] Obtain Alice’s authentic public key .

[2-2] Represent the message in binary string m of length k.

[2-3] Choose a random binary error vector z of length n having at most t 1’s.

[2-4] Compute the binary vector .

[2-5] Send the ciphertext c to Alice.

3. Decryption: Alice receives Bob’s message m and uses her private key to recover c from m. Alice performs:

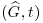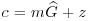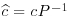[3-1] Compute , where P−1 is the inverse of the matrix P.

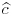[3-2] Use the decoding algorithm for the code generated by G to decode to .

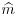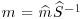[3-3] Compute . This m is thus the original plaintext.

Theorem 11.1 (Correctness of McEliece’s cryptosystem) In McEliece’s cryptosystem, m can be correctly recovered from c.

Proof: Since

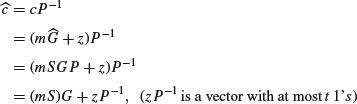
the decoding algorithm for the code generated by G corrects 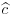to 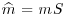. Now applying S−1 to 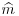, we get mSS−1 = m, the required original plaintext.

Remark 11.1 The security of McEliece’s cryptosystem is based on error-correcting codes, particularly the Goppa; if the Goppa code is replaced by other error-correcting codes, the security will be severely weakened. The McEliece’s cryptosystem has two main drawbacks:

(1) the public key is very large and

(2) there is a message expansion by a factor of n/k.

It is suggested that the values for the system parameters should be n = 1024, t = 50, and 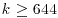. Thus for these recommended values of system parameters, the public key has about 219-bits, and the message expansion is about 1.6. For these reasons, McEliece’s cryptosystem receives little attention in practice. However, as McEliece’s cryptosystem is the first probabilistic encryption and, more importantly, it has resisted all cryptanalysis including quantum cryptanalysis, it may be a good candidate to replace RSA in the post-quantum cryptography age.

Problems for Section 11.1

1. Compare the main parameters (such as encryption and decryption complexity, cryptographic resistance, ease of use, secret-key size, and public-key size, etc.) of RSA and McEliece systems.

2. Show that decoding a general algebraic code is NP-complete.

3. Write an essay on all possible attacks for the McEliece coding-based cryptosystem.

11.2 Lattice-Based Cryptography

Cryptography based on ring properties and particularly lattice reduction is another promising direction for post-quantum cryptography, as lattice reduction is a reasonably well-studied hard problem that is currently not known to be solved in polynomial-time, or even subexponential-time on a quantum computer. There are many types of cryptographic systems based on lattice reduction [2–4]. In this section, we give a brief account of one if the lattice based cryptographic systems, the NTRU encryption scheme. NTRU is rumored to stand for Nth-degree TRUncated polynomial ring, or Number Theorists eRe Us. Compared with RSA, it is a rather young cryptosystem, developed by Hoffstein, Pipher, and Silverman [5] in 1995. We give a brief introduction to NTRU, more information can be found in [6].

Algorithm 11.2 (NTRU encryption scheme) The NTRU encryption scheme works as follows:

1. Key generation:

[1-1] Randomly generate polynomials f and G in Df and Dg, respectively, each of the form:

(11.1)

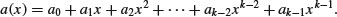
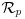[1-2] Invert f in to obtain fp, and check that G is invertible in fq.

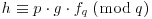[1-3] The public key is . The private key is the pair (f, fp).

2. Encryption:

[2-1] Randomly select a small polynomials r in Dr.

[2-2] Compute the ciphertext

(11.2)

3. Decryption:

[3-1] Compute ,

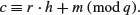
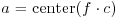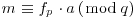[3-2] Recover m from c by computing . This is true since

(11.3)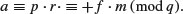

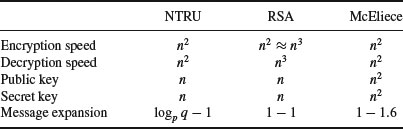
In Table 11.1, we present some information comparing NTRU to RSA and McEliece.

Table 11.1 Comparison among NTRU, RSA, and McEliece

Problems for Section 11.2

1. Give a critical analysis of the computational complexity of the NTRU cryptosystem.

2. NTRU is currently considered quantum resistant. Show that NTRU is indeed quantum resistant, or may not be quantum resistant.

3. Lattice-based cryptography is considered to be quantum resistant. However, if not designed properly, it may be broken by traditional mathematical attacks without using any quantum techniques. For example, the Cai–Cusick lattice-based cryptosystem [8] was recently cracked completely by Pan and Deng [9]. Show that the Cai–Cusick lattice-based cryptosystem can be broken in polynomial-time by classical mathematical attacks.

4. It is widely considered that multivariate public key cryptosystems (MPKC, see [7]) are quantum resistant. The usual approach to polynomial evaluation is FFT-like, whereas quantum computation makes good use of FFT to sped-up the computation. With this in mind, show that MPKC may not be quantum resistant.

11.3 Quantum Cryptography

It is evident that if a practical quantum computer is available, then all public-key cryptographic systems based on the difficulty of IFP, DLP, and ECDLP will be insecure. However, the cryptographic systems based on quantum mechanics, called quantum cryptography, will still be secure even if a quantum computer is available. So, quantum cryptography is a type of cryptography using quantum mechanics against quantum mechanics. In this section some basic ideas of quantum cryptography are introduced. More specifically, a quantum analog of the Diffie–Hellman–Meikle key-exchange/distribution system, proposed by Bennett and Brassard in 1984 [10], will be addressed.

First let us define four polarizations as follows:

(11.4)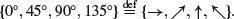

The quantum system consists of a transmitter, a receiver, and a quantum channel through which polarized photons can be sent. By the law of quantum mechanics, the receiver can either distinguish between the rectilinear polarizations 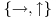, or reconfigure to discriminate between the diagonal polarizations 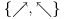, but in any case, cannot distinguish both types. The system works in the following way:

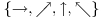1. Alice uses the transmitter to send Bob a sequence of photons, each of them should be in one of the four polarizations . For instance, Alice could choose, at random, the following photons

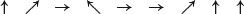
to be sent to Bob.

2. Bob then uses the receiver to measure the polarizations. For each photon received from Alice, Bob chooses, at random, the following type of measurements :

3. Bob records the result of his measurements but keeps it secret:

4. Bob publicly announces the type of measurements he made, and Alice tells him which measurements were of correct type:

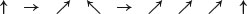
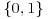5. Alice and Bob keep all cases in which Bob measured the correct type. These cases are then translated into bits and thereby become the key:

6. Using this secret key formed by the quantum channel, Bob and Alice can now encrypt and send their ordinary messages via the classic public-key channel.

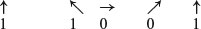
An eavesdropper is free to try to measure the photons in the quantum channel, but, according to the law of quantum mechanics, he cannot in general do this without disturbing them, and hence, the key formed by the quantum channel is secure.

Problems for Section 11.3

1. Explain what the main features of quantum cryptography are.

2. Explain why the quantum key distribution is quantum computing resistant.

3. Use the idea explained in this section to simulate the quantum key distribution and to generate a string of 56 characters for a DES key.

4. Use the idea explained in this section to simulate the quantum key distribution and to generate a stream of 128 or 256 characters for an AES key.

11.4 DNA Biological Cryptography

The world was shocked by a paper [12] of Adleman (the “A” in the RSA) , who demonstrated that an instance of the NP-complete problem, more specifically, the Hamiltonian Path Problem (HPP), can be solved in polynomial-time on a DNA biological computer (for more information on biological computing, see for example, [13] and [14]. The fundamental idea of DNA-based biological computation is that of a set of DNA strands. Since the set of DNA strands is usually kept in a test tube, the test tube is just a collection of pieces of DNA. In what follows, we shall first give a brief introduction to the DNA biological computation.

Definition 11.1 A test tube (or just tube for short) is a set of molecules of DNA (i.e., a multi-set of finite strings over the alphabet 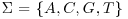). Given a tube, one can perform the following four elementary biological operations:

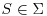(1) Separate or Extract: Given a tube t and a string of symbols , produce two tubes +(T, S) and −(T, S), where +(T, S) is all the molecules of DNA in t which contain the consecutive subsequence S and −(T, S) is all of the molecules of DNA in t which do not contain the consecutive sequence S.

(2) Merge: Given tubes T1, T2, produce the multi-set union :

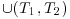(11.5)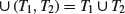

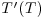(3) Detect: Given a tube t, output “yes” if t contains at least one DNA molecule (sequence) and output “no” if it contains none.

(4) Amplify: Given a tube t produce two tubes and 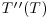such that

(11.6)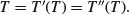

Thus, we can replicate all the DNA molecules from the test tube.

These operations are then used to write “programs” which receive a tube as input and return either “yes” or “no” or a set of tubes.

Example 11.1 Consider the following program:

(1) Input(T)

(2) T1 = −(T, C)

(3) T2 = −(T1, G)

(4) T3 = −(T2, T)

(5) Output(Detect(T3))

The model defined above is an unrestricted one. We now present a restricted biological computation model:

Definition 11.2 A tube is a multi-set of aggregates over an alphabet 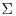which is not necessarily 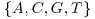. (An aggregate is a subset of symbols over ). Given a tube, there are three operations:

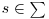(1) Separate: Given a tube t and a symbol , produce two tubes +(T, S) and −(T, S) where +(T, S) is all the aggregates of t which contains the symbols S and −(T, S) is all of the aggregates of t which do not contain the symbol S.

(2) Merge: Given tube T1, T2, produce

(11.7)

(3) Detect: Given a tube t, output “yes” if t contains at least one aggregate, or output “no” if it contains none.

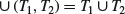
Example 11.2 (3-colorability problem) Given an n vertex graph G with edges e1, e2, ⋅⋅⋅, ez, let

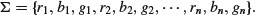
and consider the following restricted program on input

(1) Input(T).

(2) for k = 1 to z. Let :

a. Tred = +(T, ri) and Tblue or green = −(T, ri).

b. Tblue = +(Tblue or green, bi) and Tgreen = −(Tblue or green, bi).

c. Tgoodred = −(Tred, rj).

d. Tgoodblue = −(Tblue, bj).

e. Tgoodgreen = −(Tgreen, gj).

f.

g.

(3) Output(Detect(T)).

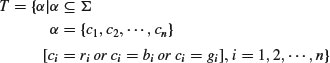
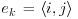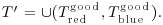
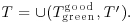
Theorem 11.2 (Lipton, 1994) Any SAT problem in n variables and m clauses can be solved with at most 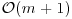separations, 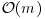merges, and one detection.

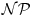The above theorem implies that biological computation can be used to solve all problems in , although it does not mean all instances of 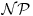can be solved in a feasible way. From a computability point of view, neither the quantum computation model nor the biological computation model has more computational power than the Turing machine. Thus we have an analog of the Church–Turing Thesis for quantum and biological computations:

Quantum and biological computation thesis: An arithmetic function is computable or a decision problem is decidable by a quantum computer or by a biological computer if and only if it is computable or decidable by a Turing machine.

This means that from a complexity point of view, both the quantum computation model and the biological computation model do indeed have some more computational power than the Turing machine. More specifically, we have the following complexity results about quantum and biological computations:

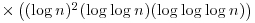(1) Integer factorization and discrete logarithm problems are believed to be intractable in Turing machines; no efficient algorithms have been found for these two classical, number-theoretic problems, in fact, the best algorithms for these two problems have the worst-case complexity . But however, both of these two problems can be solved in polynomial-time by quantum computers.

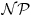(2) The famous Boolean Formula Satisfaction Problem (SAT) and directed Hamiltonian Path Problem (HPP) are proved to be -complete, but these problems, and in fact any other 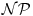-complete problems, can be solved in polynomial biological steps by biological computers.

Now we are in a position to discuss the DNA-based cryptography. We first study a DNA analog of one-time pad (OTP) encryption; its idea may be described as follows.

(1) Plaintext encoding: The plaintext: M is encoded in DNA strands.

(2) Key generation: Assemble a large OTP in the form of DNA strands.

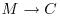(3) OTP substitution: Generate a table that randomly maps all possible strings of such that there is a unique reverse mapping .

(4) Encryption: Substitute each block of M with the ciphertext C given by the table, to get .

(5) Decryption: Reverse the substitutions to get .

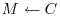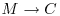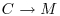The DNA implementation of the above scheme may be as follows:

(1) Plaintext in DNA: Set one test tube of short DNA strands for M.

(2) Ciphertext in DNA: Set another test tube of different short DNA strands for C.

(3) Key generation: Assemble a large OTP in the form of DNA strands.

(4) OTP substitution: Map M to C in a random yet reversible way.

(5) Encryption – DNA substitution OTDs: Use long DNA one-time pads containing many segments; each contains a cipher word followed by a plaintext word. These word-pair DNA strands are used as a lookup table in conversion of plaintext into ciphertext for .

(6) Decryption; Just do the opposite operation to the previous step for .

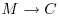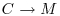Just the same as stream cipher, we could use the operation XOR, denoted by 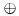to implement the DNA OTP encryption as follows.

(1) DNA plaintext test tube: Set one test tube of short DNA strands for M.

(2) DNA ciphertext test tube: Set another test tube of different short DNA strands for C.

(3) Key Generation: Assemble a large OTP in the form of DNA strands.

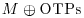(4) Encryption: Perform to get cipher strands; remove plaintext strands.

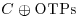(5) Decryption: Perform to get back plaintext strands.

Problems for Section 11.4

1. Explain how DNA computing can be used to solve the Hamiltonian Path Problem (HPP).

2. Explain what the main features of DNA biological cryptography are.

3. Explain why DNA biological cryptography is quantum computing resistant.

4. DNA molecular biologic cryptography, for example, Reif’s one-time pad DNA cryptosystem developed in 2004 [41], is a new development in cryptography. Give a description of the Reif’s DNA-based one-time pads.

5. Write an essay to compare the main features of classic, quantum and DNA cryptography.

11.5 Bibliographic Notes and Further Reading

Quantum-computing resistant, or quantum-attack resistant, or just quantum resistant cryptography is an important research direction in modern cryptography, since once a practical quantum computer can be built, all the public-key cryptography based on IFP, DLP, and ECDLP can be broken in polynomial-time. As Bill Gates noted in his book [11]:

We have to ensure that if any particular encryption technique proves fallible, there is a way to make an immediate transition to an alternative technique.

We need to have quantum resistant cryptographic systems ready at hand, so that we can use these cryptosystems to replace these quantum attackable cryptosystems. In this chapter, we only discussed some quantum resistant cryptographic systems, including quantum cryptography, interested readers should consult the following references for more information: [19–39]. Note that in the literature, quantum-computing resistant cryptography is also called post-quantum cryptography. Springer publishes the proceedings of the post-quantum cryptography conferences [42–45].

Just the same as quantum computing and quantum cryptography, DNA molecular computation is another type of promising computing paradigm and cryptographic scheme. Unlike the traditional computing model, DNA molecular computing is analog, not digital, so it opens a completely different phenomena to solve the hard computational problem. As can be seen from our above discussion, DNA computing has the potential to solve the NP-completeness problems such as the famous Hamiltonian Path Problem (HPP) and the Satisfiability Problem (SAT). Of course there is a long way to go to truly build a practical DNA computer. The reader may consult the following references for more information on DNA computing and cryptography: [46–54].

Chaos-based cryptography [16–18] may be another good candidate for quantum resistant cryptography; it is suggested that readers consult [15] for more information.

References

1. R. J. McEliece, A Public-Key Cryptosystem based on Algebraic Coding Theory, JPL DSN Progress Report 42–44, 1978, pp. 583–584.

2. A. K. Lenstra, H. W. Lenstra, Jr., and L. Lovász, “Factoring Polynomials with Rational Coefficients”, Mathematische Annalen, 261, 1982, pp. 515–534.

3. H. W. Lenstra, Jr., “Lattices”, Algorithmic Number Theory, edited by J.P. Buhler and P. Stevenhagen, Cambridge University Press, 2008, pp. 127–182.

4. P. Q. Nguyen and B. Vallée, The LLL Algorithm: Survey and Applications, Springer, 2011.

5. J. Hoffstein, J. Pipher, and J. H. Silverman, “A Ring-Based Public-Key Cryptosystem”, Algorithmic Number Theory ANTS-III, Lecture Notes in Computer Science 1423, Springer, 1998, pp. 267–288.

6. J. Hoffstein, N. Howgrave-Graham, J. Pipher et al., “NTRUEncrypt and NTRUSign: Efficient Public Key Algorithmd for a Post-Quantum World”, Proceedings of the International Workshop on Post-Quantum Cryptography (PQCrypto 2006), 23–26 May 2006, pp. 71–77.

7. J. Ding, J. E. Gower, and D. S. Schmidt, Multivariate Public Key Cryptosystems, Springer, 2006.

8. J. Y. Cai and T. W. Cusick, “A Lattice-Based Public-Key Cryptosystem”, Information and Computation, 151, 1–2, 1999, pp. 17–31.

9. Y. Pan and Y Deng, “Cryptanalysis of the Cai-Cusick Lattice-Based Public-Key Cryptosystem”, IEEE Transactions on Information Theory, 57, 3, 2011, pp. 1780–1785.

10. C. H. Bennett and G. Brassard, “Quantum Cryptography: Public Key Distribution and Coin Tossing”, Proceedings of the IEEE International Conference on Computers Systems and Singnal Processing, IEEE Press, 1984, pp. 175–179.

11. B. Gates, The Road Ahead, Viking, 1995.

12. L. M. Adleman, “Molecular Computation of Solutions to Combinatorial Problems”, Science, 266, 11 November 1994, pp. 1021–1024.

13. L. M. Adleman, “On Constructing a Molecular Computer”, DNA Based Computers. Edited by R. Lipton and E. Baum, American Mathematical Society, 1996, pp. 1–21.

14. E. Lamm and R. Unger, Biological Computation, CRC Press, 2011.

15. L. Kocarev and S. Lian, Chaos-Based Cryptography, Springer, 2011.

16. I. MishkovskiK and L. Kocarev, “Chaos-Based Public-Key Cryptography”, In: [15], Chaos-Based Cryptography. Edited by Kocarev and Lian, pp. 27–66.

17. D. Xiao, X. Liao, and S. Deng, “Chaos-Based Hash Function”, In: [15], Chaos-Based Cryptography, Edited by Kocarev and Lian, 2011, pp. 137–204.

18. E. Solak, “Cryptanalysis of Chaotic Ciphers”, In: [15], Chaos-Based Cryptography, Edited by Kocarev and Lian, 2011, pp. 227–254.

19. C. H. Bennett, “Quantum Cryptography using any two Nonorthogonal Sates”, Physics Review Letters, 68, 1992, pp. 3121–3124.

20. C. H. Bennett, “Quantum Information and Computation”, Physics Today, October 1995, pp. 24–30.

21. C. H. Bennett, G. Brassard, and A. K. Ekert, “Quantum Cryptography”, Scientific American, October 1992, pp. 26–33.

22. E. R. Berlekampe, R. J. McEliece, and H. van Tilburg, “On the Inherent Intractability of Certain Coding Problems”, IEEE Transaction on Information Theory, IT-24, 1978, pp. 384–386.

23. D. Bruss, G. Erdélyi, T. Meyer, et al., “Quantum Cryptography: A Survey”, ACM Computing Surveys, 39, 2, 2007, Article 6, pp. 1–27.

24. E. F. Canteaut and N. Sendrier, “Cryptanalysis of the Original McEliece Cryptosystem”, Advances in Cryptology – AsiaCrypto’98, Lecture Notes in Computer Science 1514, Springer, 1989, pp. 187–199.

25. P-L. Cayrel and M. Meziani, “Post-Quantum Cryptography: Code-Based Signatures”, Advances in Computer Science and Information Technology – AST/UCMA/ISA/ACN 2010, Lecture Notes in Computer Science 6059, Springer, 2010, pp. 82–99.

26. H. Dinh, C. Moore, and A, Russell, “McEliece and Niederreiter Cryptosystems That Resist Quantum Fourier Sampling Attacks”, Advances in Cryptology – Crypto 2011, Lecture Notes in Computer Science 6841, Springer, 2011, pp. 761–779.

27. R. J. Hughes, “Cryptography, Quantum Computation and Trapped Ions”, Philosophic Transactions of the Royal Society London, Series A, 356, 1998, pp. 1853–1868.

28. H. Inamori, A Minimal Introduction to Quantum Key Distribution, Centre for Quantum Computation, Clarendon Laboratory, Oxford University, 1999.

29. H. K. Lo, “Quantum Cryptography”, Introduction to Quantum Computation and Information. Edited by H. K. Lo, S. Popescu and T. Spiller, World Scientific, 1998, pp. 76–119.

30. H. Lo and H. Chau, “Unconditional Security of Quantum key Distribution over Arbitrary Long Distances”, Science, 283, 1999, pp. 2050–2056.

31. H. Niederreiter, “Knapsack Type Cryptosystems and Algebraic Coding Theory”, Problem of Control and Information Theory, 15, 1986, pp. 159–166.

32. M. A. Nielson and I. L. Chuang, Quantum Computation and Quantum Information, 10th Anniversary Edition, Cambridge University Press, 2010.

33. R. A. Perlner and D. A. Cooper, “Quantum Resistant Public Key Cryptography”, Proceedings of the 8th Symposium on Identity and Trust on the Internet, Gaithersburg, MD, April 14–16, ACM Press, 2009, pp. 85–93.

34. W. Trappe and L. Washington, Introduction to Cryptography with Coding Theory, 2nd Edition, Prentice-Hall, 2006.

35. H. van Tilborg (editor), Encyclopedia of Cryptography and Security, Springer, 2005.

36. H. van Tilburg, “On the McEliece Public-Key Cryptography”, Advances in Cryptology – Crypto’88, Lecture Notes in Computer Science 403, Springer, 1989, pp. 119–131.

37. J. L. Walker, Codes and Curves, American Mathematical Society and Institute for Advanced Study, 2000.

38. C. P. Williams, Explorations in Quantum Computation, 2nd Edition, Springer, 2011.

39. S. Y. Yan, Cryptanalyic Attacks on RSA, Springer, 2009.

40. S. Y. Yan, Quantum Attacks on Public-Key Cryptography, Springer, 2012.

41. A. Gehani, T. H. LaBean, and J. H. Reif, “DNA-Based Cryptography”, Molecular Computing, Lecture Notes in Computer Science 2950, Springer, 2004, pp. 167–188.

42. D. J. Bernstein, J. Buchmann, and E. Dahmen (Editors), Post-Quantum Cryptography, Springer, 2010.

43. J. Buchmann and J. Ding (Editors), Post-Quantum Cryptography, Lecture Notes in Computer Science 5299, Springer, 2008.

44. N. Sendrier (Editor), Post-Quantum Cryptography, Lecture Notes in Computer Science 6061, Springer, 2010.

45. B. Yang (Editor), Post-Quantum Cryptography, Lecture Notes in Computer Science 7071, Springer, 2011.

46. R. D. Barish, P. Rothemund, and E. Winfree, “Two Computational Primitives for Algorithmic Self-Assembly: Copying and Counting”, Nano Letters, 5, 12, 2005, pp. 2586–2592.

47. Y. Benenson, B. Gill, and U. Ben-Dor, et al., “An Autonomous Moleular Computer for Logical Control of Gene Expressions”, Nature, 429, 6990, 2004, pp. 423–429.

48. D. Boneh, C. Dunworth and R. Lipton, et al., “On the Computational Power of DNA”, Discrete Applied Mathematics, 71, 1, 1996, pp. 79–94.

49. D. Bray, “Pretein Molecular as Computational Elements in Living Cells”, Nature, 376, 6538, 1995, pp. 307–312.

50. T. Gramb, A. Bornholdt, and M. Grob, et al., Non-Standard Computation, Wiley-VCH, 1998.

51. R.Lipton, “DNA Solution of Hard Computational Problems”, Science, 268, 5210, 1995, pp. 542–545.

52. R. Unger and J. Moult, “Towards Computing with Protein”, Proteine, 63, 2006, pp. 53–64.

53. E. Winfree, F. Liu, and L. A. Wenzler, et al., “Design and Self-Assembly of Two-Dimensional DNA Crystals”, Nature, 394, 6693(1998), pp. 539–544.

54. N. Jonoska, G. Paun, and G. Rozenberg (editors), Molecular Computing, Lecture Notes in Computer Science 2950, Springer, 2004.