Part II

Computational Number Theory

Computational number theory is a new branch of mathematics. Informally, it can be regarded as a combined and disciplinary subject of number theory and computer science, especially the theory of computation:

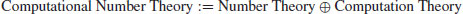
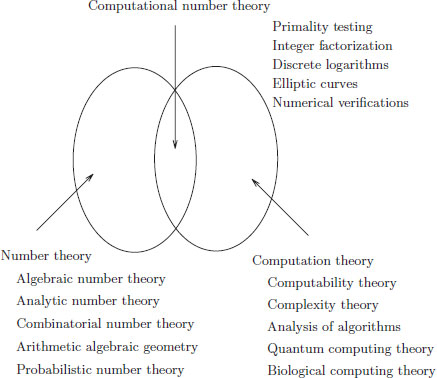
The purposes of computational number theory are two-fold: (1) using computing techniques to solve number theoretic problems, and (2) using number theoretic techniques to solve computer science problems. In this part of the book, we shall concentrate on using computing techniques to solve number theoretic problems that have connections and applications in modern cryptography. More specifically, we shall study computational methods (algorithms) for solving the:

1. Primality Testing Problem (PTP)

2. Integer Factorization Problem (IFP)

3. Discrete Logarithm Problem (DLP)

4. Elliptic Curve Discrete Logarithm Problem (ECDLP)

with a special emphasis on the last three infeasible (intractable) number theoretic problems, as they play a central role in the security of the cryptographic schemes and protocols in the next part of the book.