Part IV

Quantum Resistant Cryptography

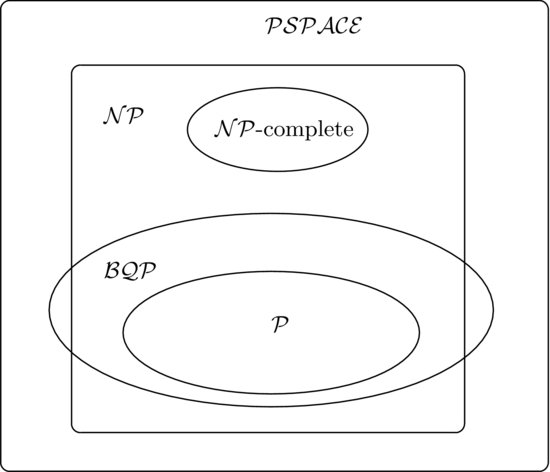
Quantum computers have gained widespread interest because some problems of particular cryptographic interest are known to be in bounded error quantum polynomial-time (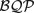), but suspected to be outside polynomial-time (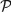). The following figure shows the conjectured relationship of 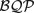to other common complexity classes. For example, the following three infeasible problems can all be solved in 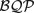on a quantum computer, but can only be solved in subexponential-time on a classical computer:

• Integer Factorization Problem (IFP),
• Discrete Logarithm Problem (DLP),
• Elliptic Curve Discrete Logarithm Problem (ECDLP).

Of course, the quantum algorithms for solving these problems are necessarily to be run on a practical quantum computer. Thus, once a practical quantum computer can be built, all the cryptographic schemes based on IFP, DLP, and ECDLP will be insecure. In this chapter, we shall first show some quantum algorithms for solving IFP, DLP, and ECDLP, and hence for breaking IFP-, DLP-, and ECDLP-based cryptography. Then we shall present some quantum-computing resistant cryptographic schemes. By quantum-computing resistant cryptography, we mean that the quantum-computing attacks are invalid against these cryptographic schemes. This is possible, because quantum computers are not just faster versions of classical electronic computers, but use a different paradigm for computation. They would speed-up some problems such as IFP and DLP by a large factor and others problems such as the Linear Coding Problem not at all.