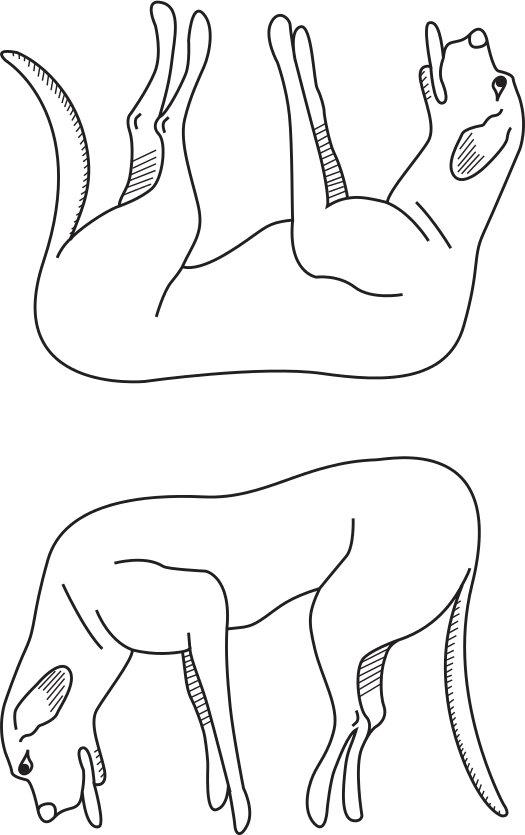
1
THE THREE RABBITS
Can you rearrange the positions of the three rabbits and the three ears so that each rabbit has two ears?

If you’re reading this in a Devon church, don’t look up!
More than a dozen churches in Devon have medieval wooden carvings on their ceilings that display the solution. In fact, the image of three rabbits, or hares, sharing their ears is a symbol that appears in many sacred sites across the northern hemisphere, the earliest dating from sixth-century China. The largest cluster of examples, however, is in Devon, where the linked leporine lugs are sometimes known as the Tinners’ Rabbits, possibly because wealth from local tin mines helped build and maintain the churches hundreds of years ago.
The simple symmetry of the three rabbits makes them a powerful mystical symbol, an easy metaphor for ideas of eternity and beauty. Yet part of their allure is their elegance as a puzzle, in which the image makes sense when seen one way, but not when seen in another. We are attracted to images that play with our sense of perception. Puzzles are by their nature mesmerising; they spin our heads right round.
This canine conundrum dates from 1849, when it appeared in the first issue of The Family Friend, a lifestyle magazine in book form aimed at the Victorian housewife. It’s the original version of a visual illusion that has been reinvented many times since, in which you must draw four lines on an image in order to bring two animals back to life.
3
GOOD NEIGHBOURS
A woman opened the door and her dog walked in. The dog had the neighbour’s pet rabbit in its mouth. The rabbit was dead. Distraught, the woman went next door immediately to apologise. The neighbour smiled. ‘Don’t worry, my rabbit was not harmed.’
Why was the rabbit not harmed?
The mysticism around the three rabbits also turns on rabbit behaviour in the wild. The breeding rate of bunnies has made them age-old symbols of fertility and rebirth, anthropomorphic shorthand for the highly sexed. Prolific procreation is their principal protection against a profusion of prowling predators. Reproduction is ripe for mathematical analysis. Indeed, one of the most famous problems in mathematical literature is about a rapidly expanding rabbit family.
In the Liber Abaci, the thirteenth-century book that introduced Arabic numerals to Europe, Leonardo of Pisa, better known as Fibonacci, set the following problem. Start with a pair of rabbits. If they produce a pair of offspring every month, and if every new pair becomes fertile after a month, again producing another pair every month, how many pairs are there at the end of 12 months? Saving you the bother of calculation, the monthly totals are (1), 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233 and 377, an ordered list of numbers known – thanks to this problem – as the Fibonacci sequence.
(We start with 1 pair. At the end of the first month, this pair has bred, so we have 2 pairs. At the end of the second month, the first pair has bred again but the second pair is not yet fertile, so we have a total of 3 pairs. At the end of the third month, the first and second pairs have now bred, but the third is not yet fertile, giving a total of 5 pairs. And so on.)
The Fibonacci sequence is one of the few number sequences known beyond mathematics. It has many intriguing properties. For example, each term is the sum of the previous two (1 + 2 = 3, 2 + 3 = 5, 3 + 5 = 8, and so on). This recursive process models natural growth – for plants as well as bucktoothed mammals – which is why the number of spirals in cauliflower, Romanesco broccoli, pinecones, pineapples and sunflower heads is nearly always a number in the Fibonacci sequence. Do check, next time you’re at the supermarket.
Fibonacci hit on a fascinating piece of pure mathematics. Yet how well does his problem reflect the real world? In other words, did he create an accurate model of the reproductive practices of rabbits?
To Fibonacci’s credit, he got the gestation period about right. Rabbits take a month to have babies, and can be impregnated again within minutes of giving birth. Poor things. So, theoretically, a doe can have 12 litters a year. On the other hand, she becomes fertile more slowly, after about six months, and she has more children, on average about six kits per litter. Armed with the relevant zoological data we can update Fibonacci’s historic rabbit riddle.
4
A FERTILE FAMILY
How many descendants does a female rabbit have in her lifetime if:
Rabbits become fertile after six months.
Once fertile, a doe produces every month a litter of six kits, three of which are female.
The life span of a rabbit is seven years.
Of course, these details still paint a simplified picture. In the wild, the life span of a rabbit is only about a year. After a few years the fertility of female rabbits drops off. Environmental factors such as available space and food will limit the rate of growth. Nevertheless, the question provides a theoretical estimate of the upper bound of potential bunny reproduction, a scientific analysis of what it really means to breed like rabbits.
I’ll give you full marks if you can work out the formula for how to calculate the answer. To get the exact figure you might need some computer assistance. For those who aren’t masters of technology (or Excel), look in the back. But before you do, estimate what you think the answer is. If you get it right to within two powers of 10 – i.e., up to 100 times more, or 100 times less – treat yourself to a meal of lapin à la moutarde and a bottle of Chablis. You will be amazed.
The next puzzle is about rabbits. Sorry, I mean ribbits.
5
A BUNCH OF HOPS
Ten lily pads are positioned in a straight line across a pond. A frog sits on the leftmost lily.

At any stage, a frog can either jump to the next lily along, or hop over that lily and land on the lily two positions along.
If the frog never goes backwards, how many different ways are there for it to reach the lily on the right?
Let’s hop on. From an animal famed for its jumps, to one famed for its humps.
The camel is a double celebrity in puzzle-land.
First, it gives a bravura performance as the protagonist in a medieval puzzle about transporting grain. Secondly, it appears in a traditional puzzle about a family feud. (I’ll start with the first and get to the second later.)
The gist of the grain transportation problem is this: what is the best strategy to get a camel to deliver grain from A to B, given that the more the camel walks, the more of the grain it will require as food? The first question of this type appeared in the foundational work of modern-day puzzledom, Alcuin of York’s eighth-century manuscript, Propositiones ad Acuendos Juvenes, or Problems to Sharpen the Young. A caravan of similar problems about walking and eating, or walking and drinking, trod over the dunes in the following centuries.
6
CROSSING THE DESERT
Four Bedouin tribesmen, each with a camel, are standing together at the edge of a desert. The group must deliver an important package to a camp in the middle of the desert, four days’ camel-ride away. Camels can only carry enough water for five days. If the Bedouin cooperate, and are able to transfer water between camels in the desert without losing any due to spillage and evaporation, how is it possible for one of them to deliver the package and all of them return to their starting point with only 20 days’ supply of water?
Alcuin’s camel problem is a brilliant example of a piece of fun that evolved into a serious area of mathematical research. In the twentieth century, the grain-guzzling camel was upgraded to a gas-guzzling machine. The ‘jeep problem’ asks you to find the best way to drive as far as you can from your source of petrol if you can only carry a finite amount of petrol at a time, but are allowed to deposit it at drop-off points and return to pick up more. This problem has obvious applications in exploration and warfare. Indeed, the first detailed analysis of the problem was funded in 1946 by the United States Army Air Forces. If your exploratory mission requires you to bring your own fuel – because you are traversing the Antarctic, flying over enemy territory, or discovering new areas of the solar system – you will grapple with exactly this type of logistical issue.
7
SAVE THE ANTELOPE
You are a vet working in the Sahara when you hear that an endangered antelope has broken its leg 400 miles away from your practice. You decide to rescue the animal in your jeep, the specifications of which are:
It does 100 miles to the gallon.
The tank has a maximum capacity of a gallon of petrol.
In addition to what’s in the tank, the jeep will carry four one-gallon canisters of petrol.
There are no petrol stations between you and the injured animal, so in order to drive long distances you have to drop off canisters at certain points and return to pick them up later. You can only drop off canisters that are full. You can return to base as many times as you like to refuel.
How do you reach the animal and bring it to your practice using only 14 gallons of petrol?
Study of the jeep problem led to a staggering result, the kind you can’t quite believe even though the maths proves it’s true. Let’s imagine there is a service station with an unlimited supply of fuel, and you have a jeep with a finitely sized tank. It is possible to drive as far as you like from that service station using only petrol from there. In other words, you could theoretically drive all the way around the world in a Fiat Uno using only petrol that you took with you from London. (Like the problem above, the strategy relies on making many sorties to drop off fuel and pick it up later. If n is the number of miles you can drive on a full tank, you can get as far as n with no drop-offs. You’ll have to take my word that you can reach a distance of n (1 + 1/3) with a single fuel drop-off, you can reach n (1 + 1/3 + 1/5) with two drop-offs, and the more drop-offs you are able to make, the further and further you can travel, even though the extra distances you can go get smaller and smaller. Since the series 1 + 1/3 + 1/5 + 1/7 + … is a divergent series, meaning that by including more and more terms it can be made to exceed any finite value, the distance the jeep can travel will also exceed any finite value.)
*
The other classic problem about camels involves three children arguing about their inheritance. The kids are in a hump about who gets the humps. The puzzle in the form presented below dates from the nineteenth century. In recent years it has been reinvented as a morality tale about how a random act of generosity solves an apparently intractable problem.
A man’s dying wish is that his herd of 17 camels is divided among his three children, such that the eldest child gets half of them, the middle child gets a third of them, and the youngest a ninth of them. The children are unable to decide how many camels each is to receive because of the arithmetical impossibility of dividing 17 by 2, 3 or 9 and getting a whole number of camels. (No camels are to be harmed during the solving of this problem.)
In order to resolve the dispute, the children approach a wise old woman and explain the situation. She listens intently. To the children’s surprise, she fetches her own camel and gives it to them.
‘Now that you have 18 camels,’ she says, ‘you can divide them up in accordance with your father’s wishes.’
The eldest child takes 9 camels, which is half of them, the middle child takes 6, which is a third, and the youngest takes 2, a ninth. However, 9 camels + 6 camels + 2 camels = 17 camels. In other words, one camel is left over. ‘I’ll take my camel back, thanks,’ says the old woman, and she and her camel walk away.
The puzzle here is to explain the apparent contradiction in why a group of objects that cannot be cleanly divided into a half, a third and a ninth can be divided into those proportions when an extra object is added and then taken away. (I’ll explain how it works in the Answers section.)
The wise woman who negotiates peace among feuding siblings makes for a charming parable, in which the eighteenth camel represents a fresh idea that resolves a deadlocked situation.
She returns to help another family in a similar predicament.
8
THE THIRTEEN CAMELS
A man leaves 13 camels to his three children in the following proportions: to the eldest, half; to the middle child, a third; to the youngest, a quarter. The children can’t decide how many each should get, because you cannot divide 13 by 2, 3 or 4 without inflicting severe pain on a camel.
They consult a wise old woman to resolve their dispute. How does she fix it?
Camels and horses are historically the two most popular riding animals. Have you ever wondered which is faster? Or slower?
9
CAMEL VS. HORSE
Kamal has a camel and Horace has a horse. The friends are arguing about which animal is slower, so they decide to race them along a one-mile stretch of track, with the winner being the one that reaches the finish line last. They get in their saddles. But, predictably, they just stand there, since no one wants to start first and risk being the first to finish. An hour later, Ada shows up. She asks what’s going on. The men get out of their saddles and explain. Ada says a few words, at which point the men sprint to the animals, jump on, and race to the finish line as fast as possible.
What was Ada’s advice?
The following animal puzzle also involves two friends riding at speed in a straight line.
10
THE ZIG-ZAGGING FLY
Two cyclists are racing towards each other along a straight road. When they are 20 miles apart, a fly on the nose of one of the cyclists starts flying in a straight line towards the nose of the other cyclist. When it reaches the nose of the other cyclist, it immediately turns around and flies back towards the first cyclist, and it carries on flying between the cyclists’ noses as they approach each other.
If the cyclists are both cycling at a constant speed of 10 miles an hour, and the fly flies at a constant speed of 15 miles an hour, how far has the fly flown when the cyclists meet?
You can solve this the hard way or the easy way. The hard way is to calculate how far the fly travels before it touches the nose of the second cyclist, and then how far it travels back before touching the nose of the first cyclist, and so on, adding up a series of decreasing lengths.
I’ll leave it to you to find the easy way.
The zig-zagging fly is part of mathematical folklore because of an episode involving one of the twentieth century’s greatest scientists, John von Neumann, the Hungarian-American who made many important advances in economics, computer science and physics.
On being told the puzzle by a friend, von Neumann solved it instantly in his head.
‘So you saw the trick,’ his friend remarked.
‘No,’ he replied. ‘I just summed the distances.’
Geniuses can sometimes be a bit stupid.
The next puzzle is also about insects moving in one dimension. And like the last one, its apparent unwieldiness unravels from a simple insight.
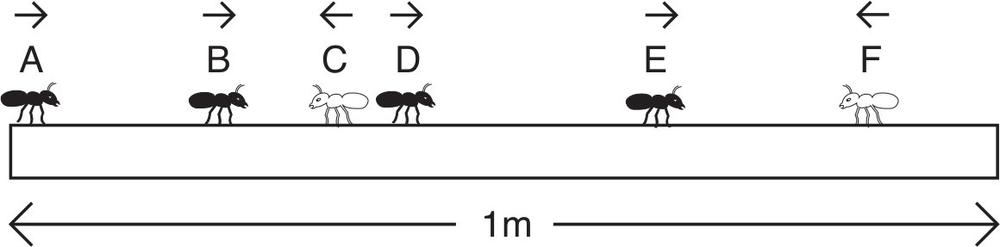
11
THE ANTS ON A STICK
Six ants are walking along the edge of a 1m stick, as illustrated below. Aggie, Bozo, Daz and Ezra are walking from left to right as we look at the diagram. Carlos and Freya are walking from right to left. The ants always walk at exactly 1cm per second. Whenever they bump into another ant, they immediately turn around and walk in the other direction. When they get to either end of the stick, they fall off.
Their starting positions from the left end of the stick are: Aggie 0cm, Bozo 20cm, Daz 38.5cm, Ezra 65.4cm and Freya 90.8cm. Carlos’s position is not known – all we know is that he starts somewhere between Bozo and Daz.
Which ant is the last to fall off the stick? And how long will it be before he or she does fall off?
Now for a puzzle involving rubber. It’s stretching, that’s for sure. Like the previous question, it is also about invertebrates travelling from one end of a long piece of material to the other.
12
THE SNAIL ON THE ELASTIC BAND
A snail lies at one end of an elastic band that is 1km long, as shown below. It crawls towards the other end at a constant rate of 1cm per second. At the end of each second, the elastic band is stretched by a kilometre. In other words, when the snail has crawled 1cm the elastic is 2km long, when it has crawled 2cm the elastic is 3km long, and so on.
Show how the snail eventually reaches the end of the elastic band.

The snail sets off on a daunting task that appears to get even more dispiriting as each second passes. If it travels at only 1cm a second, and the elastic band stretches by 1km a second, our initial reaction is that the snail will always be getting further and further from its target destination rather than nearer to it. It’s a beautiful puzzle, however, because the snail does get there in the end. (We need to assume that the elastic band stretches uniformly as far as possible, that the snail never dies.)
To get a sense of why the snail is not doomed to eternal crawling, consider its distance from the left end of the elastic band. (It’s a mathematical snail, so consider it as a point, starting at the band’s left edge.) After one second, the snail has travelled to a point 1cm along, which on stretching becomes a point 2cm along, since stretching the elastic from 1km to 2km has the effect of doubling the distance between any two points. After another second the snail is 3cm from the left end, which on stretching instantly becomes 4.5cm, since stretching the elastic from 2km to 3km has the effect of multiplying the distance between any two points by 3/2. In other words, the snail is carried forward by the stretching and covers an increasing distance each second, which gives us some hope that it might be able to traverse its ever-expanding floor.
I included the snail puzzle because the result is spectacular, even though the full proof requires a piece of information that, while familiar to mathematicians, will not be known to everyone. Astute readers will notice, however, that this result can be deduced from material I have already shared in preceding pages.
Now for some puzzles that require no technical mathematics at all.
13
ANIMALS THAT TURN HEADS

Move a single matchstick so that the horse changes direction.

The dog is facing left. Can you make him face right – while keeping his tail pointing upwards - by moving only two matches?
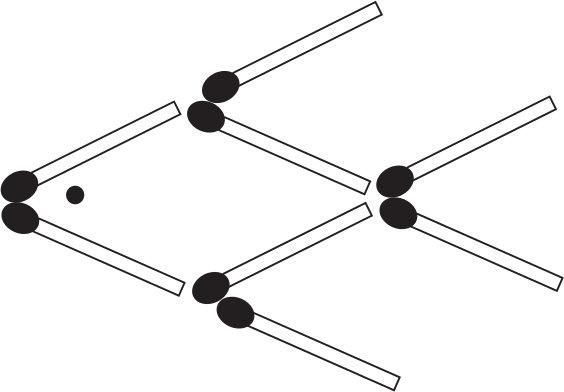
The fish has a blueberry for an eye. Can you move the blueberry and three matches to make the fish point the other way?
14
BANISHING BUGS FROM THE BED
Your bedroom is full of critters that can wriggle and creep along any solid surface, but cannot swim.
You want to stop these pesky bugs getting into your bed. It’s easy to stop them getting up from the floor: you stand each leg of the bed in a bucket of water.
But how do you stop them from crawling up to the ceiling and falling down on your sheets? A gutter like the one shown below won’t work since the bugs could fall onto the edge of the gutter and then crawl round and drop onto the bed.
What construction will keep your bed bug-free?

Suspending a canopy, or mosquito net, over the bed is not the solution, since the critters will crawl all over it, and might well crawl underneath it and up to the bed. Were you to find a way to hermetically seal this canopy to the floor, you would still have to open it to reach the bed, and when you did the bugs would be able to crawl through the opening too.
The next puzzle might sound like a sitcom skit, but it has genuine mathematical content. Everyday language is full of ambiguities and assumed knowledge. Mathematical statements, on the other hand, are precise. The challenge of the puzzle is to apply mathematical rigour to a non-mathematical statement for comic effect. Let your inner pedant run free!
15
THE DUMB PARROT
The owner of a pet shop never lies and is very precise with his words. A customer asks him about the parrot in a cage on his counter. ‘This bird is extremely intelligent,’ he replies. ‘She will repeat every word that she hears.’ The customer buys the bird. A few days later, however, the customer returns. ‘I’m furious! I spoke to the parrot for hours but the stupid bird has not repeated a single thing!’
Given that the pet shop owner did not lie, how is this possible?
Here’s one for nothing. The parrot could be dead. The Monty Python solution. Easy. But can you come up with at least four more reasons for the bird’s silence that – while possibly far-fetched – do not contradict the owner of the shop?
So far, I’ve included puzzles involving mammals, arthropods, a fish, an amphibian and a bird. Only one class of animal is left.
16
CHAMELEON CAROUSEL
A colony of chameleons on an island currently comprises 13 green, 15 blue and 17 red individuals. When two chameleons of different colours meet, they both change their colours to the third colour. Is it possible that all chameleons in the colony eventually have the same colour?
Heron of Alexandria lived in the first century BCE. He is the most important mathematician to share a name with a common animal, which is surely enough to get him a mention in this chapter. Heron invented many ingenious contraptions that were way ahead of their time, including a vending machine, a mechanical puppet theatre and a steam engine. He also discovered a theorem that is the basis of many splendid puzzles. I’ll illustrate it here in the context of two houses and a road. It states that the shortest path from house A to house B via a point on the road is the one marked below, constructed by drawing a line to B', where B' is a reflection of B across the road. The line from A to B' is straight, so it is obviously the shortest path from A to B', and it is also the same length as the path from A to B via the road. You are now equipped to solve the next puzzle, about an animal taking the optimal path to lunch.
17
THE SPIDER AND THE FLY
A fly lands on the inside of a cylindrical glass tumbler, 2cm from the rim, as illustrated right. A spider is on the opposite side of the glass, 2cm from the bottom. The glass has a height of 8cm and a circumference of 12cm. If the fly remains stationary, what is the shortest distance the spider must crawl in order to reach it?

Look again at the earlier image of the houses and the road. The angle at which the path from A hits the road is the same as the angle at which the path leaves the road for B. In other words, the picture illustrates the law of reflection of light, which states that when light hits a mirror, the angle of incidence is equal to the angle of reflection. (Imagine the road is a side view of a mirror, and A is a light source. The beam that leaves A and reflects to B is exactly the one illustrated by the black line.) Heron knew the law of reflection of light. Using his theorem about minimal distance, he became the first person to deduce that light always takes the shortest path.
18
THE MEERKAT IN THE MIRROR
A meerkat is looking at itself in a wall mirror. It sees its reflection perfectly framed: the top of its head reaches the top of the mirror and its feet reach the bottom.
What happens when the meerkat steps back from the mirror? Does it see less of itself in the mirror, or do gaps open up above its head and beneath its toes?
Assume that the wall mirror is vertical, and that the meerkat is rod-straight upright when looking at itself.
Meerkats lend themselves well to the previous problem since the one thing everyone knows about them is that they like to stand up. What about the behavioural traits of real cats? They are mischievous, independently minded and like to move around at night.
19
CATCH THE CAT
A straight corridor has seven doors along one side. Behind one of the doors sits a cat. Your mission is to find the cat by opening the correct door. Each day you can open only one door. If the cat is there, you win. If the cat is not there, the door closes, and you must wait until the next day before you can open a door again. The cat is restless and every night it moves to sit behind another door. The door it moves to is either the one immediately to the left or the one immediately to the right of where it was previously.
How many days do you need to make sure you will find the cat?

The question is asking you to find a strategy that guarantees you will catch the cat in a fixed number of days, whichever door it starts behind and wherever it moves in the night. The key to the solution is to begin with a smaller number of doors, find the pattern, and then increase the number of doors. I’ll get you started. Imagine there are only three doors. If you open the middle door on two consecutive days you are guaranteed to get the cat, since if the cat is not behind the middle door on day one, it must be behind either of the end doors. And if it is behind either of the end doors on day one, it has no option but to move behind the middle door on day two. If there are four doors, you can catch the cat in four days. I’m not going to explain the strategy, but you will purr with delight when you work it out. Remember, the cat will only move to a door immediately to its right or its left, and it may return to a door it was behind previously.
Predatory aggression is a common theme in puzzles. Usually, but not always, felt by frustrated solvers.
20
MAN SPITES DOG
A house is surrounded by a five-foot-high wall. Its front door can only be reached by a path, which you enter from the main gate.
A postman arrives at the gate. He sees a dog in the garden. The dog sees him, springs up and runs to the gate to attack him, stopped only by its leash, which is tied to a tree. The dog is barking and straining at the leash, trying to get as near to the postman as possible. The dog will attack the postman if he walks along the path.
How might the postman manage to deliver the letter safely?
21
THE GERM JAR
X and Y are two types of germ that exhibit the following predator-and-prey behaviour.
X germs: a single X will eat one Y per minute if any are available. Once an X has eaten a Y, the X multiplies to become two Xs.
Y germs: a single Y will double every minute into two Ys, unless it is eaten by an X.
In other words, an X only doubles after devouring a Y, but a Y will double on its own. A scientist has a jar containing 30 Y germs, and places inside it a single X germ.
After how many minutes are there no more Y germs left in the jar?
A famous recreational problem about predation concerns a man thrown into a circular arena with a hungry lion. If the man and the lion have the same maximum running speed, and both have limitless energy, will the lion eventually catch the man or can the man always evade the lion?
The problem is notable not only because it captured the imagination of the mathematical community, but also because for several decades people kept getting it wrong. The German mathematician Richard Rado proposed the problem in 1932. (Like the protagonist of the puzzle, Rado, a Jewish man in Berlin, was also fearing for his life. A year later he fled the Nazi regime to Britain.) Originally, the prevailing view was that the man was doomed, that in a bounded circular arena he would not be able to escape the jaws of the hungry lion. Yet in the 1950s, the Cambridge professor Abram S. Besicovitch discovered a strategy in which the man would, in fact, be able to dodge the lion ad infinitum. The man was saved. While the proof is too involved for this book, the strategy is easy to understand: the man will evade capture if, for each time interval, he runs in a line perpendicular to the line between him and the lion, choosing the direction that keeps him closer to the centre point of the circle.
Here’s a simpler challenge involving a circular arena and a peckish predator.
22
THE FOX AND THE DUCK
A duck is floating in the middle of a circular lake. A fox is prowling round the bank. The fox can run four times faster than the duck can paddle, and the fox will always position itself in the best possible spot on the side of the lake to catch the duck.
The duck can only fly from dry land. Is there a way for the duck to reach the side of the lake – and fly to safety – without being caught by the fox?
At first glance, the duck’s prospects don’t look good.
Let’s say that the fox is at the top of the lake, as shown in the image opposite. If the duck decides to paddle in a straight line as fast as it can in the opposite direction to the fox, then by the time it gets to the shore the fox will be waiting. We can work this out with some basic geometry. The duck’s path is a distance of r, the radius of the lake. The fox’s path is a distance of πr. (It travels half the circumference of the lake, and the circumference of a circle is 2πr, where the value of π is approximately 3.14.) The fox thus needs to run a distance that is 3.14 times greater than the distance the duck has to paddle. Since the fox is four times faster than the duck, it will get there first.
The challenge is to plot a path that allows the duck to step onto land at a point the fox can’t get to quick enough.

John von Neumann – the speed-solver of the ‘zig-zagging fly’ (Problem 10) – is considered, together with the economist Oskar Morgenstern, to be the founding father of game theory, the mathematical analysis of decision-making. The games von Neumann was originally thinking about were parlour games, but as the subject expanded it found wide applications in many fields, such as psychology, philosophy, politics, sociology and, of course, recreational puzzles. Game theory models the behaviour of individuals who interact according to certain rules and aim to ‘win’ – in other words, to get the best possible outcome for themselves. Such as the lions in the following puzzle.
23
THE LOGICAL LIONS
Ten lions are in a pen. Their favourite food is sheep. The lions know, however, that any lion that eats a sheep will become drowsy, and is likely to be eaten by another lion if one is nearby. A lion that eats a lion will also become drowsy, and thus also risks being eaten.
A sheep is put in the pen. Each of the lions is desperate to eat it, but will only do so if they are sure they will not be eaten themselves.
What happens to the sheep?
(Extra question: what happens if there are 11 lions in the pen at the start?)
To avoid ambiguity, if the sheep is eaten, it must be eaten by one lion only, and not shared between the pack. We can assume that lions will always act in their best interests and are impeccable logicians.
Pigs are highly intelligent creatures, even the ones that don’t have PhDs. In 1979, Basil Baldwin and G. B. Meese, of the Babraham Institute, Cambridge, conducted an experiment involving pigs, as described in the following puzzle. The experiment became famous because it showed that game theory perfectly modelled the animals’ behaviour.
24
TWO PIGS IN A BOX
Two pigs live in a box: a bigger, dominant one, and a smaller, subordinate one. The box is arranged such that when a lever is pressed at one end, food is dispensed in a bowl at the other. The distance between the lever and the bowl means that the pig pressing the lever will get to any newly dispensed food second.
Which pig eats better?
After all this talk of food, here’s some wine to wash down the final puzzle in this chapter.
25
TEN RATS AND ONE THOUSAND BOTTLES
You have inherited a collection of one thousand bottles. All the bottles contain wine except one, which contains poison. The only way to discover what’s in a bottle is to drink it. If you drink poison, however, you die.
Thankfully, you have 10 rats. If a rat sips poison, or poison mixed with wine, it will die after exactly one hour. If a rat drinks wine, it survives. How do you determine which bottle is poisoned exactly one hour after the first rats are given their first sips?
With unlimited time, 10 rats are plenty to help you discover the poisoned bottle. For example, you could separate the thousand bottles into 10 batches of 100, and allocate each batch to a different rat. Let the rats take a sip from every bottle in their batch. An hour later one rat will be dead, narrowing the options for the poisoned bottle to the 100 bottles in that rat’s batch. Separate these 100 into nine smaller batches, one each for the nine remaining rats. Again, a dead rat will pinpoint the contaminated batch. Carry on in this way and the rats, now metaphorically as well as literally rat-arsed, will soon narrow the options to a single poisoned bottle.
Poisoning rats in series, however, is unnecessarily long-winded. The solution is to poison in parallel, in other words to get the rats to quaff contrasting concoctions concurrently. At least one rat will remain alive during your attempt at mass intoxication.
Dodging death sets us up for the next chapter. It begins with a curious animal, perhaps the best known puzzler of all.