⊂ Y.Separation Axioms
It is often desirable for a topologist to be able to assign to a set of objects a topology about which he knows a great deal in advance. This can be done by stipulating that the topology must satisfy axioms in addition to those generally required of topological spaces.
One such collection of conditions is given by means of axioms called Ti or separation axioms. These stipulate the degree to which distinct points or closed sets may be separated by open sets. Let (X, τ) be a topological space.
| T0 axiom: | If a,b ∈ X, there exists an open set O ∈ τ such that either a ∈ O and b ∉ O, or b ∈ O and a ∉ O. | |
| T1 axiom: | If a,b ∈ X, there exist open sets Oa, Ob ∈ τ containing a and b respectively, such that b ∉ Oa and a ∉ Ob. | |
| T2 axiom: | If a,b ∈ X, there exist disjoint open sets Oa and Ob containing a and b respectively. | |
| T3 axiom: | If A is a closed set and b is a point not in A, there exist disjoint open sets OA and Ob containing A and b respectively. | |
| T4 axiom: | If A and B are disjoint closed sets in X, there exist disjoint open sets OA and OB containing A and B respectively. | |
| T5 axiom: | If A and B are separated sets in X, there exist disjoint open sets OA and OB containing A and B respectively. |
If (X, τ) satisfies a Ti axiom, X is called a Ti space. A T0 space is sometimes called a Kolmogorov space and a T1 space, a Fréchet space. We will conform to common practice and call a T2 space a Hausdorff space.
It follows from the Ti axioms that T0 spaces are characterized by the fact that no two points can be limit points of each other. Similarly, T1 spaces are characterized by points being closed, and T2 spaces by points being the intersection of their closed neighborhoods. T3 spaces may be characterized either by the fact that each open set contains a closed neighborhood around each of its points, or by the property that each closed set is the intersection of its closed neighborhoods. A space is T4 iff every open set O contains a closed neighborhood of each closed set contained in O. It is T5 iff every subset Y contains a closed neighborhood of each set A ⊂ Y° where ⊂ Y.
Each of these axioms is independent of the axioms for a topological space; in fact there exist examples of topological spaces which fail to satisfy any Ti axiom (Example 21). But they are not independent of each other, since for instance, axiom T2 implies axiom T1 and axiom T1 implies axiom T0. There are, on the other hand, T0 spaces which fail to satisfy every other separation axiom (Example 53) and T1 spaces which do not satisfy any separation axiom but the T0 axiom (Example 18); similarly, there are T2 spaces which fail to be T3, T4 or T5 (Example 75). Furthermore, neither the T3 axiom nor the T4 axiom implies any of the other separation axioms (Examples 90.4 and 21.8) nor is either generally implied by them though in compact spaces T2 implies T4 but not T5 (Example 86). The T5 axiom does however imply T4, though it is independent of the other separation axioms.
REGULAR AND NORMAL SPACES
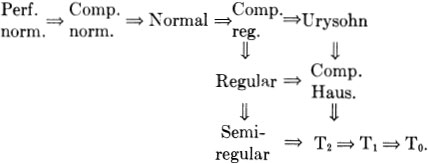
More important than the separation axioms themselves is the fact that they can be employed to define successively stronger properties. To this end, we note that if a space is both T3 and T0, it is T2, while a space that is both T4 and T1 must be T3. The former spaces are called regular, and the latter normal.
Specifically a space X is said to be regular if and only if it is both a T0 and a T3 space; to be normal if and only if it is both a T1 and a T4 space; to be completely normal if and only if it is both a T1 and a T5 space. Thus, we have the following sequence of implications:
Examples 86, 82, 75, 18, and 53 show that the implications are not reversible. A T4 space (or T5 space) must be a T1 space in order to guarantee that it is a T3 space, for there are T4 spaces (and T5 spaces) which are T0 and yet fail to be T3 (Example 55).
The use of the terms “regular” and “normal” is not uniform throughout the literature. While some authors use these terms interchangeably with “T3 space” and “T4 space” respectively, others refer to our T3 space as a “regular” space and vice versa, and similarly permute “T4 space” and “normal.” This allows the successively stronger properties to correspond to increasing Ti axioms. We prefer, however, to allow a Ti space to be a space satisfying the corresponding Ti axiom, and content ourselves with labeling the successively stronger properties with unique terminology.
COMPLETELY HAUSDORFF SPACES
We will now introduce two variations of the separation properties. The first involves the use of closed neighborhoods in place of open sets in axioms T2, T3, and T4.
Since in normal spaces every open set O contains a closed neighborhood of each closed set contained in O, if X is a normal space and if A and B are disjoint closed subsets, there exist open sets OA and OB containing A and B, respectively, such that 
A ∩ B = ∅. So the use of closed neighborhoods in place of open sets in the definition of a normal space yields the same class of spaces.
Similarly, if X is a regular space, A is a closed subset, and b is a point not in A, then there are open sets OA and Ob containing A and b respectively such that A ∩ b = ∅ However, there are Hausdorff spaces which have two points which do not have disjoint closed neighborhoods (Example 75). Thus, we present the following new axiom.
T2 axiom: |
If a and b are two points of a topological space X, there exist open sets Oa and Ob containing a and b, respectively, such that a ∩ b = ∅ |
A T2 space will be called a completely Hausdorff space. It is clear that every regular space is completely Hausdorff and every completely Hausdorff space is Hausdorff. Since there are completely Hausdorff spaces which fail to be regular (Example 78), the completely Hausdorff property is intermediate in strength between the properties Hausdorff and regular.
COMPLETELY REGULAR SPACES
The second variation of the separation axioms concerns the existence of certain continuous, real-valued functions. A Urysohn function for A and B, disjoint subsets of a space X, is a continuous function f: X → [0, 1] such that f|A = 0 and f|B = 1.
Urysohn’s famous lemma asserts that if A and B are disjoint closed subsets of a T4 space, there exists a Urysohn function for A and B. Conversely, if there is a Urysohn function for any two disjoint closed sets A and B in a space X, then X is a T4 space. But the existence of such a function does not guarantee that X is a T1 space and thus a normal space (Example 5).
However, the statement for regular spaces analogous to Urysohn’s lemma is false (Example 90), so we give the following new separation axiom:
T axiom: |
If A is a closed subset of a space X and b is a point not in A, there is a Urysohn function for A and {b}. |
Then every T space is a T3 space, though not necessarily a T2 space (Example 5) unless it is also a T0 space. Such a space, which is both T0 and T, will be called completely regular, or Tychonoff. Thus completely regular spaces are regular, Hausdorff, and therefore T1. Since points are closed in normal spaces, it follows from Urysohn’s lemma that normal spaces are completely regular. There are, however, regular spaces which fail to be completely regular (Example 90) and completely regular spaces which fail to be normal (Example 82).
Although normal spaces are T, T4 spaces need not be (Example 55). But if a T4 space is also T3, even though possibly not normal, it must nevertheless be T for if the point p is disjoint from the closed set A in a T3 space, then there is an open neighborhood of A disjoint from p. The complement B of this neighborhood is a closed set disjoint from A, so if the space is also T4, we can apply Urysohn’s lemma to produce a Urysohn function for A and B. This function is clearly a Urysohn function for A and {p} also.
We summarize the Ti implications and counterexamples in Figure 1 where the numbers in parentheses indicate examples. In addition, we have the following simple diagram, in which none of the arrows reverse, and where the numbers refer to appropriate counterexamples:
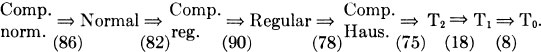
FUNCTIONS, PRODUCTS, AND SUBSPACES
All the separation properties are topological properties, that is, they are preserved under homeomorphisms. However, certain of the properties are preserved under less restrictive functions.
If X and Y are topological spaces, and f : X → Y is a closed bijection, and X is T0, T1, Hausdorff, or completely Hausdorff, then Y is T0, T1, Hausdorff, or completely Hausdorff, respectively. In particular, if τ1 ⊂ τ2 are topologies for X, the identity function from (X, τ1) to (X, τ2) is closed ; hence, if (X, τ1) is T0, T1, Hausdorff, or completely Hausdorff, then so is (X, τ2). We call τ2 an expansion of τ1 and note that expansion preserves the above separation properties. The stronger separation properties are not, in general, preserved under expansion (Example 66).
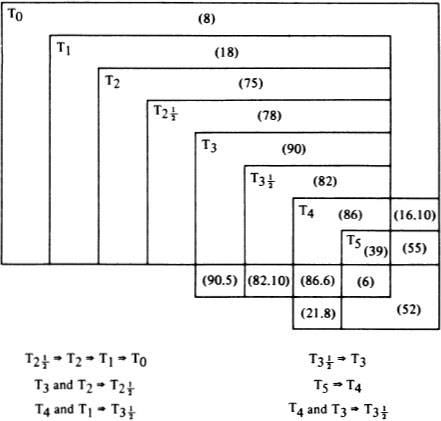
Figure 1.
Most separation properties are, however, preserved under products. If X = Π Xα, then X is a T0, T1, Hausdorff, completely Hausdorff, regular, or completely regular space if and only if each of the Xα is T0, T1, Hausdorff, completely Hausdorff, regular, or completely regular, respectively. If X is normal or completely normal, each Xα is normal or completely normal, but the converse does not hold (Example 84).
Normality diverges from the remainder of the separation properties in the case of subspaces, also. For every subspace of a T0, T1, Hausdorff, completely Hausdorff, regular, or completely regular space is T0, T1, Hausdorff, completely Hausdorff, regular, or completely regular, respectively. But only closed subspaces of normal spaces need be normal (Example 86). However, every subspace of a completely normal space is completely normal, since, a space is completely normal iff every subspace is normal. In fact, a space is T5 iff every subspace is T4.
ADDITIONAL SEPARATION PROPERTIES
Urysohn’s lemma guarantees for T4 spaces the existence of a Urysohn function for any two disjoint closed sets. Requiring such a function for a point and a closed set gave the T property which was stronger than axiom T3. When applied to two points this requirement yields a condition even stronger than completely Hausdorff (Example 80). We call a space with a Urysohn function for any two points a Urysohn space.
A T4 space in which every closed set is a Gδ is often called perfectly T4. A perfectly T4 space which is also T1 will be called perfectly normal. Every perfectly normal space is completely normal, but not conversely (Example 24).
Since each open set in a T3 space contains a closed neighborhood around each of its points, every open set in a T3 space can be written as the union of regular open sets. Since the converse is not true (Example 81), we will call semiregular all T2 spaces in which the regular open sets form a basis for the topology. Semiregular spaces are not necessarily either completely Hausdorff (Example 81) or Urysohn (Example 80).
Figure 2.
If we add these new properties to the basic separation axiom structure, we obtain the summary Figure 2. The implications are best illustrated by
