SECTION 3

Compactness

A space satisfies a certain separation axiom only if the topology contains enough open sets to provide disjoint neighborhoods for certain disjoint sets. Compactness, however, limits the number of open sets in a topology, for every open cover of a compact topological space must contain a finite sub-cover. This difference between the separation axioms and the various forms of compactness is illustrated in the extreme by the double pointed finite complement topology (Example 18.7) which is not even T₀ yet does satisfy all the forms of compactness.

GLOBAL COMPACTNESS PROPERTIES

A topological space X is compact if every open cover contains a finite subcover; equivalently, X is compact if it satisfies the finite intersection axiom, that is, if every family of closed subsets whose intersection is empty contains a finite subfamily whose intersection is empty. For if {A_α} is any family of closed sets such that ∩ A_α = Ø, then {X − A_α} is an open cover which has a finite subcover {X – A_αk|k ≤ n}. By De Morgan’s Law, iff . Conversely, if the family {O_α} is an open cover of X, then since , there is a finite subfamily such that . By De Morgan’s Law, . An equivalent subbasis condition for compactness is given by Alexander’s Compactness Theorem: if a topological space X has a subbasis S such that from every cover of X by elements of S, a finite sub-cover can be selected, then X is compact. The condition is clearly necessary, but the proof of sufficiency uses the axiom of choice.

Two generalizations of compactness may be obtained by weakening the requirement that subcovers be finite. A topological space is called σ-compact if it is the union of countably many compact sets, while a space is called Lindelöf if every open cover has a countable subcover. Clearly every compact space is σ-compact and every σ-compact space Lindelöf. These implications are not reversible (Examples 28 and 51).

A topological space is called countably compact if any one of the following equivalent conditions is satisfied :

CC1:		Every countable open cover of X has a finite subcover.
CC2:		Every infinite set has an co-accumulation point in X
CC3:		Every sequence has an accumulation point in X
CC4:		Every countable collection of closed sets with an empty intersection has a finite subfamily with an empty intersection.

Condition CC₄, the countable finite intersection axiom, is equivalent to CC₁ for the same reasons that the ordinary finite intersection axiom is equivalent to compactness. Conditions CC₂ and CC₃ are equivalent to each other since a point is an ω-accumulation point of a countably infinite set iff it is an accumulation point of that set viewed as a sequence. Now if the space X has a countable open cover {O_i} with no finite subcover, we can find a set {x_n} of distinct points such that this sequence can have no ω-accumulation point in X, for every point of X has a neighborhood, namely one of the O_i to which it belongs, which intersects only finitely many points of the set. Thus CC₂ ⇒ CC₁. Conversely, if S ⊂ X is a countably infinite set without an ω-accumulation point, each x ∈ X would have an open neighborhood O_x which intersects at most finitely many points of S. For each finite subset F of S, define Then {O_F} is a countable open covering of X every finite subcollection of which includes at most finitely many points of S. Thus no finite subcollection may cover X.

Two other conditions are closely related, but not equivalent to countable compactness: a topological space is said to be sequentially compact if every sequence has a convergent subsequence, and weakly countably compact (or limit point compact) if every infinite set has a limit point. Sequential compactness clearly implies countable compactness, and since every ω-accumulation point is a limit point, every countably compact space is weakly countably compact. However, neither converse is necessarily true (Examples 105 and 106). However, in a T₁ space, weak countable compactness is equivalent to countable compactness. For assuming that a: is a limit point of a set A, but not an ω-accumulation point, implies that some open set O_x containing x contains only a finite number of points of A, say {a₁ … a_n}. But in a T₁ space, this implies that x has an open neighborhood which contains no points of A, that is, that x is not a limit point of A.

Finally, a space X is called pseudocompact if every continuous real-valued function on X is bounded. Every countably compact space X is pseudocompact, since for a continuous function f on X, the sets form a countable cover of X whose finite subcover yields a bound for the absolute value of f. Although the converse is not true (Example 9), every pseudocompact normal space is necessarily countably compact. Suppose not; then X would contain an infinite subset S = {x_n} with no ω-accumulation point. Since X is T₁, S is closed and discrete in the sub-space topology; since X is T₄, the Tietze extension theorem guarantees a continuous extension to X of the unbounded continuous function f = S → R defined by f(x_n) = n. This shows that X could not have been pseudo-compact.

The relations between the varieties of global compactness may be summarized in this diagram :

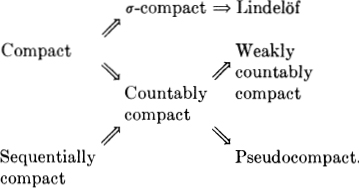
In general, none of the arrows reverse, though, trivially, every countably compact Lindelöf space is compact. So Figure 3 summarizes both the implications and counterexamples.

LOCALIZED COMPACTNESS PROPERTIES

A topological space is called locally compact if each point is contained in a compact neighborhood. Clearly every compact space X is locally compact, since X itself is a compact neighborhood of each of its points.

A common nonequivalent variation of the definition of local compactness requires that each point be contained in an open set whose closure is compact. We shall call this concept strong local compactness since every space satisfying this condition is clearly locally compact; the converse, however, is not generally true (Example 52) although it does hold in Hausdorff spaces for in such spaces compact sets are closed, so the interior of every compact neighborhood has a compact closure.

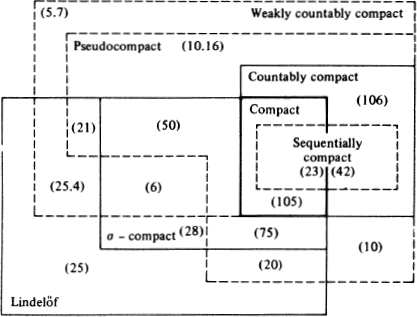
Figure 3.

A different strong form of local compactness is obtained by requiring X to be both σ-compact and locally compact: such a space is called σ-locally compact. It suffices in fact to assume X locally compact and Lindelöf, for such spaces must be σ-compact: the interiors of the compact neighborhoods cover X, so some countable number of such interiors, and therefore of compact neighborhoods, covers X.

Although both stronger properties imply local compactness, strong local compactness and σ-local compactness are independent (Examples 3 and 52). We may summarize the implications as follows:

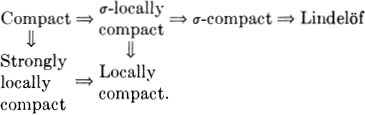
The appropriate counterexamples are summarized in Figure 4.

COUNTABILITY AXIOMS AND SEPARABILITY

Although the previous compactness properties indirectly imply limitations on the number of open sets in a topology, the countability axioms introduced in the first section directly limit the number of open sets by restricting the number of basis elements. There are three major countability properties: a topological space is separable if it has a countable dense subset, second countable if it has a countable basis, and first countable if the neighborhood system of every point has a countable local basis. Clearly, every second countable space is first countable, separable and Lindelöf, although none of these implications reverse. In fact, there are spaces which are first countable, separable and Lindelöf but not second countable (Example 51). A special property which is strictly weaker than separability (Example 20) is the countable chain condition, which is the condition that every disjoint family of open sets is countable.

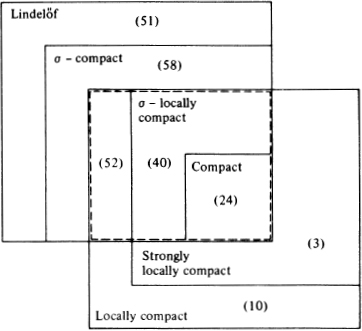
Figure 4.

In second countable spaces, compactness is equivalent to countable compactness. Similarly, in a first countable space, countable compactness is equivalent to sequential compactness, for if {s_n} is any sequence in a countably compact space X with accumulation point p ∈ X, there is a countable local base at p, say . Then a subsequence {s_ni} where s_ni ∈ V_i, converges to p.

Figure 5 summarizes the important relations between the countability axioms and compactness.

PARACOMPACTNESS

Several compactness properties which have both local and global aspects rely on the concept of a refinement of a cover. A cover {V_β} of a space X is a refinement of a cover {U_α} if for each V_β there is a U_α such that V_β ⊂ U_α. A cover is point finite if each point belongs to only finitely many sets in the covering, and it is locally finite if each point has some neighborhood which intersects only finitely many members of the cover. Finally, a cover {V_β} of X is said to be a star refinement of a cover {U_α} if for each x ∈ X there is some U_α such that x* ⊂ U_α, where x*, the star of x with respect to {V_β} is the union of all the sets V_β of which x is an element.

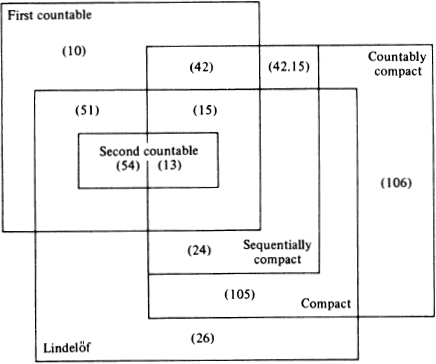
Figure 5.

A space is called metacompact (or sometimes pointwise paracompact) if every open cover has an open point finite refinement, paracompact if every open cover has an open locally finite refinement, and fully T₄ if every open cover has a star refinement. The slightly weaker conditions of countable metacompactness and countable paracompactness require only that every countable open cover have the desired type of refinement. A fully T₄ space which is also T₁ is called fully normal. As the notation implies, every fully normal space is normal, and also paracompact.

Clearly every compact space is paracompact, and every paracompact space metacompact. Although these implications are not reversible (Examples 28 and 89), every metacompact space (and therefore every paracompact space) which is also countably compact must be compact. For if {U_α} is any open covering of the metacompact space X, {U_α} has an open point finite refinement {V_β}. Now {V_β} has an irreducible (that is, a minimal) subcovering {V_γ}, for if we order subcoverings by inclusion, the intersection of a chain of subcoverings is a subcovering : if x is not covered by the intersection of the subcoverings, being contained in only finitely many V_β, it would fail to be covered by one of the elements of the chain of subcoverings, a contradiction. Now {V_γ} is a finite covering, for in each V_γ there is an x_γ belonging to no other element of the family {V_γ} since the family is minimal and if the family {V_γ} were infinite the set {x_γ} would be an infinite set with no ω-accumulation point.

Thus we have the following implications:

None of the implications is reversible, so Figure 6 can be used to summarize the necessary counterexamples.

Just as a Lindelöf countably compact space is compact every Lindelöf countably metacompact space is metacompact and every Lindelöf countably paracompact space is paracompact. Furthermore a separable metacompact space is Lindelöf. For if {U_α} is an open cover with no countable subcover, and {V_β} is a point finite refinement (uncountable, of course), and {x_δ} is a countable dense subset, then each V_β contains some x_δ so some x_δ is contained in uncountably many V_α, a contradiction to the nature of {V_β}.

COMPACTNESS PROPERTIES AND THE T_i AXIOMS

Although compactness and the separation axioms involve conflicting requirements on the number of open sets in the topology, when compactness properties are combined with the T₂ or T₃ axioms, the topology often satisfies certain higher T_i axioms. For the compactness properties, by limiting the number of open sets in a cover, allow the desired disjoint open sets to be constructed by finite intersections. As a result compact sets in T₂ or T₃ spaces have the same properties as points, namely: two disjoint compact sets in a Hausdorff space have disjoint neighborhoods, while if A is a compact subset of T₃ spaces, then for each open set U ⊃ A, there is an open V such that . Also, then, compact sets in a Hausdorff space are closed. Thus a compact Hausdorff space is T₄ since closed subsets of a compact space are compact. In fact certain conditions weaker than compactness are sufficient for this, while other compactness properties result in only weaker conclusions. The precise nature of the implications following from the assumption of the T₂ or T₃ separation axioms is pictured in Figure 7. Furthermore, certain combinations of the compactness properties and separation axioms force a space to be of the second category in itself. This type of Baire category theorem applies both to locally compact Hausdorff spaces and to countably compact regular spaces.

Figure 6.

Compact Hausdorff topologies are especially interesting since any such topology τ on a space X is both minimal Hausdorff as well as maximal compact, τ is a minimal Hausdorff topology since if τ* ⊂ τ, the identity map f: (X, τ) → (X, τ*) would be continuous. Thus if A is closed in (X,τ), it is compact (since (X, τ) is compact) and thus f(A) is compact. If τ* were Hausdorff, f(A) would be closed, and hence f would be a closed mapping—which would mean that τ ⊂ τ*. Thus no topology strictly smaller than τ can be Hausdorff. Similarly, τ is a maximal compact topology for if τ* ⊃ τ, the identity map f: (X, τ) → (X, τ*) is a continuous bijection of a Hausdorff space to a compact Hausdorff space. If τ* is also compact, f must be open, hence τ* ⊂ τ. Thus no topology strictly larger than τ can be compact. Examples 99 and 100 show that the converse statements are not necessarily true: minimal Hausdorff topologies need not be compact, and maximal compact topologies need not be Hausdorff.

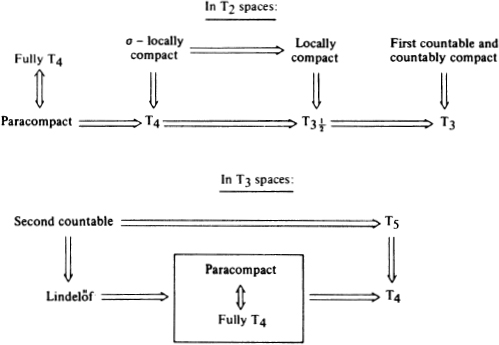
Figure 7.

We should note, finally that separable Hausdorff spaces can have cardinality not exceeding , for if D is a countable dense subset of X, the map defined by for some neighborhood U_x of x is one-to-one whenever X is Hausdorff. Thus card (X) ≤ card .

INVARIANCE PROPERTIES

It can be easily seen that most global and local compactness properties (namely those defined by covers) are weakly hereditary, that is, they are preserved in closed subspaces. But in most cases they are not preserved in open subspaces, so are not hereditary. Paracompactness and meta-compactness, similarly, are only weakly hereditary. Both first and second countability are, however, hereditary, although separability is not. In fact, separability is preserved only in open subspaces (Example 10.6).

Most compactness properties fail to be preserved by arbitrary products. The most famous exception is compactness itself, for, by Tychonoff’s theorem, the product of an arbitrary family of topological spaces is compact iff each factor space is compact. If X is compact, then in general X × Y has the compactness properties of Y. If X satisfies only weaker conditions, the situation is considerably more complex, and may be best summarized by Table 1 which indicates which properties are preserved by various types of products, and cites counterexamples where appropriate.

Table 1

PROPERTIES PRESERVED BY PRODUCTS

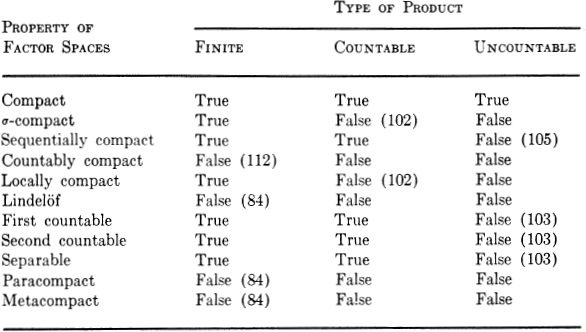
Conversely, it is often possible to infer properties of the factors given a property of the product space. This may be done most easily by observing that the projection maps are continuous, but in general, only the global compactness properties are preserved under continuous mappings. To be precise, the properties of compactness, σ-compactness, countable compactness, sequential compactness, Lindelöf, and separability are preserved under continuous maps and therefore also under projections. Local compactness, and first and second countability are preserved under open continuous maps, but not just under continuous maps (Examples 116 and 26); since projections are open and continuous, these properties also are preserved under projection maps. Paracompactness even fails to be preserved under open continuous maps (Example 11.19), although it is preserved under projections.