Image moments

In mathematics, a moment can be seen as a specific quantitative measure of a function shape. An image moment can be seen as a weighted average of image pixel intensities, or a function of such moments, encoding some interesting properties. In this sense, image moments are useful to describe some properties of the detected contours (for example, the center of mass of the object, or the area of the object, among others).

cv2.moments() can be used to calculate all the moments up to the third order of a vector shape or a rasterized shape.

The signature for this method is as follows:

retval = cv.moments(array[, binaryImage])

Therefore, in order to calculate the moments for a detected contour (for example, the first detected contour), perform the following:

M = cv2.moments(contours[0])

If we print M, we get the following information:

{'m00': 235283.0, 'm10': 75282991.16666666, 'm01': 75279680.83333333, 'm20': 28496148988.333332, 'm11': 24089788592.25, 'm02': 28492341886.0, 'm30': 11939291123446.25, 'm21': 9118893653727.8, 'm12': 9117775940692.967, 'm03': 11936167227424.852, 'mu20': 4408013598.184406, 'mu11': 2712402.277420044, 'mu02': 4406324849.628765, 'mu30': 595042037.7265625, 'mu21': -292162222.4824219, 'mu12': -592577546.1586914, 'mu03': 294852334.5449219, 'nu20': 0.07962727021646843, 'nu11': 4.8997396280458296e-05, 'nu02': 0.07959676431294238, 'nu30': 2.2160077537124397e-05, 'nu21': -1.0880470778779139e-05, 'nu12': -2.2068296922023203e-05, 'nu03': 1.0980653771087236e-05}

As you can see, there are three different types of moment (m_ji, mu_ji, nu_ji). 

The spatial moments m_ji are computed as follows:

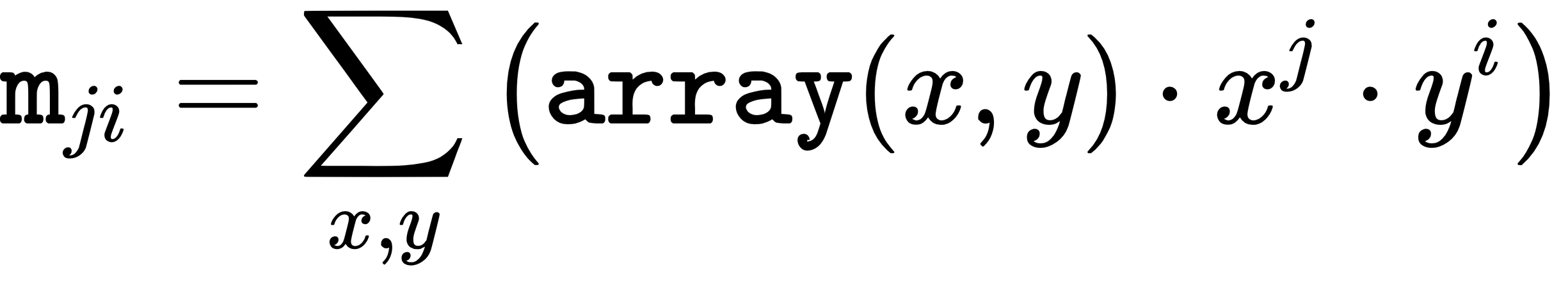
The central moments mu_ji are computed as follows:

Here, the following applies:

The preceding equation corresponds to the mass center.

Central moments are, by definition, invariant with respect to translations. Therefore, central moments are suited to describing the form of the object. However, a disadvantage of both spatial and central moments is their dependency on the size of the object. They are not scale-invariant.

Normalized central moments nu_ij are computed as follows:

Normalized central moments are, by definition, invariants to both translation and scale.

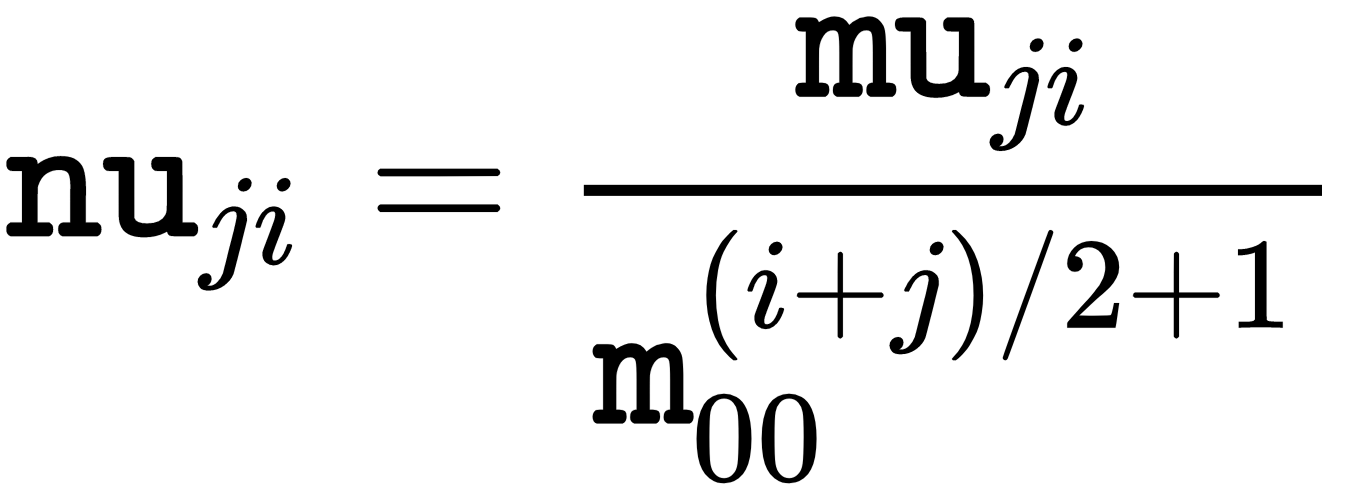
The value for the next moments is calculated as follows:

mu₀₀=m₀₀, nu₀₀=1, nu₁₀=mu₁₀=mu₀₁=mu₁₀=0

Hence, these moments are not stored.

Moments are usually classified by their order, which is calculated based on the sum (j+i) of indices j, i of the moment m_ji.

In the next subsections, further information about image moments will be given. More specifically, some object features based on moments (for example, center, eccentricity or the area of the contour, among others) will be computed. Additionally, Hu moment invariants will also be seen. Finally, Zernike moments are also introduced.