Handwritten digit recognition using SVM

We just saw how to perform handwritten digit recognition using the kNN classifier. The best accuracy was obtained by preprocessing the digits (recall the deskew() function) and computing the HOG descriptor as the feature vector used to describe each digit. Therefore, for the sake of simplicity, the next scripts, which are going to make use of SVM to classify the digits, will use the aforementioned approximation (preprocessing and HOG features).

The svm_handwritten_digits_recognition_preprocessing_hog.py script performs the handwritten digit recognition using SVM classification. The key code is shown as follows:

# Load all the digits and the corresponding labels:
digits, labels = load_digits_and_labels('digits.png')

# Shuffle data
# Constructs a random number generator:
rand = np.random.RandomState(1234)
# Randomly permute the sequence:
shuffle = rand.permutation(len(digits))
digits, labels = digits[shuffle], labels[shuffle]

# HoG feature descriptor:
hog = get_hog()

# Compute the descriptors for all the images.
# In this case, the HoG descriptor is calculated
hog_descriptors = []
for img in digits:
    hog_descriptors.append(hog.compute(deskew(img)))
hog_descriptors = np.squeeze(hog_descriptors)

# At this point we split the data into training and testing (50% for each one):
partition = int(0.5 * len(hog_descriptors))
hog_descriptors_train, hog_descriptors_test = np.split(hog_descriptors, [partition])
labels_train, labels_test = np.split(labels, [partition])

print('Training SVM model ...')
model = svm_init(C=12.5, gamma=0.50625)
svm_train(model, hog_descriptors_train, labels_train)

print('Evaluating model ... ')
svm_evaluate(model, hog_descriptors_test, labels_test)

In this case, we have used an RBF kernel:

def svm_init(C=12.5, gamma=0.50625):
    """Creates empty model and assigns main parameters"""

    model = cv2.ml.SVM_create()
    model.setGamma(gamma)
    model.setC(C)
    model.setKernel(cv2.ml.SVM_RBF)
    model.setType(cv2.ml.SVM_C_SVC)
    model.setTermCriteria((cv2.TERM_CRITERIA_MAX_ITER, 100, 1e-6))

    return model

The obtained accuracy is 98.60%, using only 50% of the digits to train the algorithm.

Additionally, when using the RBF kernel, there are two important parameters—C and γ. In this case, C=12.5 and γ=0.50625. As before, C and γ are unknown as the best for a given problem (dataset dependent). Therefore, some kind of parameter search must be done. Hence, the goal is to identify good (C and γ) where a grid-search on C and γ is recommended.

In the svm_handwritten_digits_recognition_preprocessing_hog_c_gamma.py script, two modifications are carried out in comparison with the svm_handwritten_digits_recognition_preprocessing_hog.py script. The first one is that the model is trained with 90% of the digits, and the remaining 10% is used for testing. The second modification is that a grid-search on C and γ is performed:

# Create a dictionary to store the accuracy when testing:
results = defaultdict(list)

for C in [1, 10, 100, 1000]:
    for gamma in [0.1, 0.3, 0.5, 0.7, 0.9, 1.1, 1.3, 1.5]:
        model = svm_init(C, gamma)
        svm_train(model, hog_descriptors_train, labels_train)
        acc = svm_evaluate(model, hog_descriptors_test, labels_test)
        print(" {}".format("%.2f" % acc))
        results[C].append(acc)

And finally, this is the result:

# Create the dimensions of the figure and set title:
fig = plt.figure(figsize=(10, 6))
plt.suptitle("SVM handwritten digits recognition", fontsize=14, fontweight='bold')
fig.patch.set_facecolor('silver')

# Show all results using matplotlib capabilities:
ax = plt.subplot(1, 1, 1)
ax.set_xlim(0, 1.5)
dim = [0.1, 0.3, 0.5, 0.7, 0.9, 1.1, 1.3, 1.5]

for key in results:
    ax.plot(dim, results[key], linestyle='--', marker='o', label=str(key))

plt.legend(loc='upper left', title="C")
plt.title('Accuracy of the SVM model varying both C and gamma')
plt.xlabel("gamma")
plt.ylabel("accuracy")
plt.show()

The output of this script can be seen in the next screenshot:

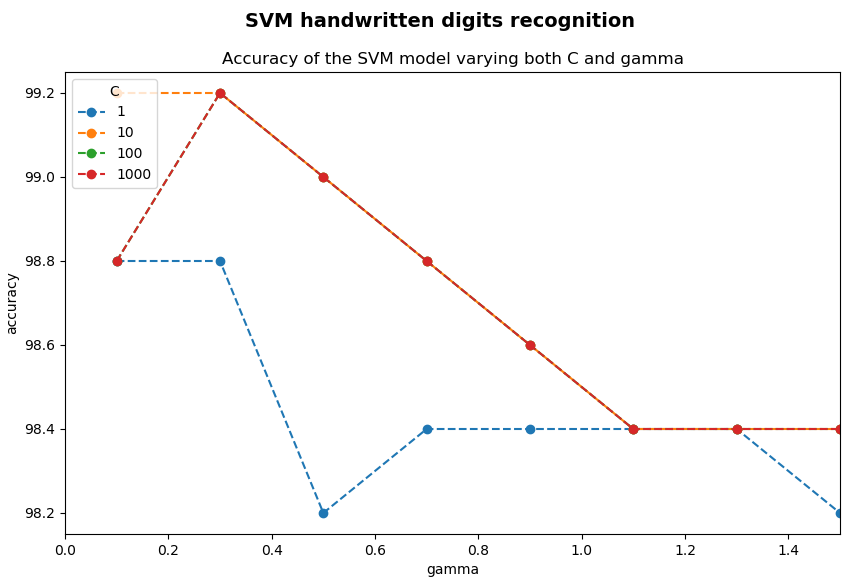
As shown, an accuracy of 99.20% is obtained in several cases. 

By comparing the kNN classifier and SVM for handwritten digit recognition, we can conclude that SVM outperforms the kNN classifier.