More functionality related to contours

So far, we have seen some contour properties derived from image moments (for example, centroid, area, roundness, or eccentricity, among others). Additionally, OpenCV provides some interesting functionality related to contours that can be also used to further describe contours.

In contours_functionality.py, we mainly use five OpenCV functions related to contours and one function that computes the extreme points of a given contour.

Before describing what each of these functions computes, it is preferable to show the output of this script, because the resulting image can help us understand each of the aforementioned functions:

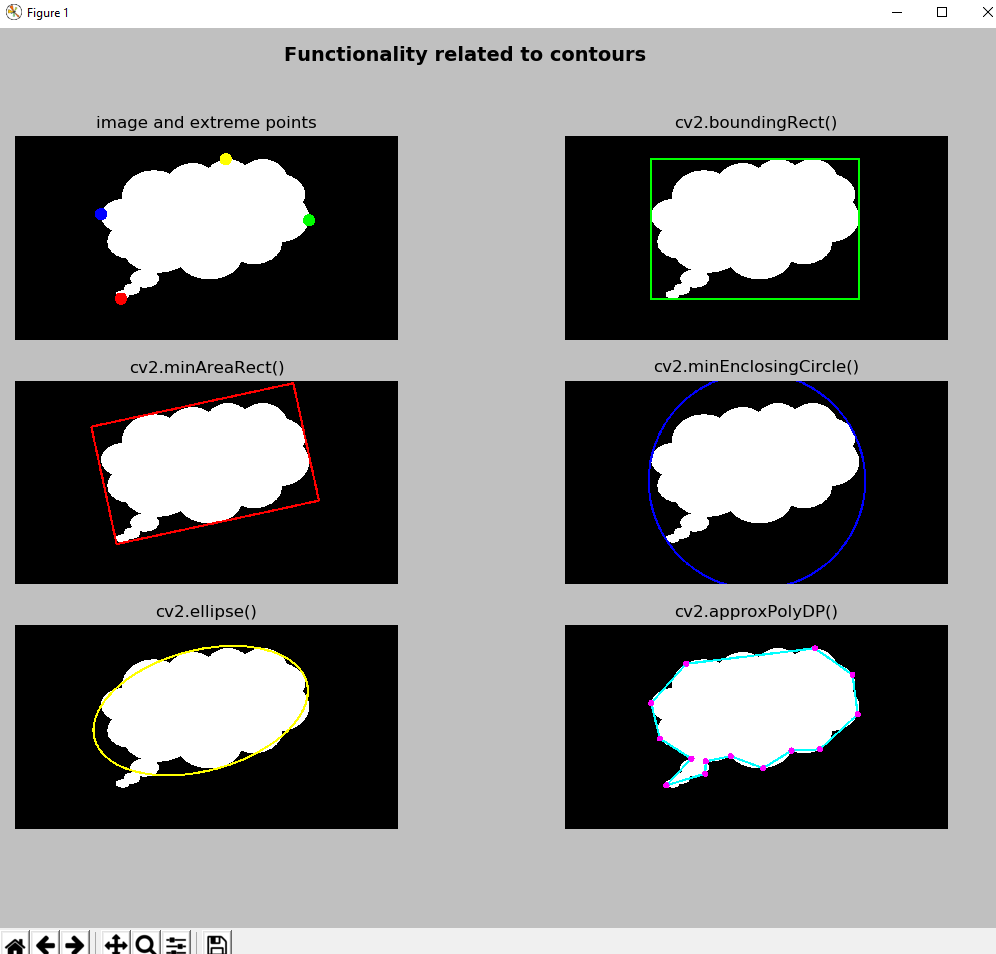
cv2.boundingRect() returns the minimal bounding rectangle enclosing all the points of the contour:

x, y, w, h = cv2.boundingRect(contours[0])

cv2.minAreaRect() returns the minimal rotated (if necessary) rectangle enclosing all the points of the contour:

rotated_rect = cv2.minAreaRect(contours[0])

In order to extract the four points of the rotated rectangle, you can use the cv2.boxPoints() function, which returns the four vertices of the rotated rectangle:

box = cv2.boxPoints(rotated_rect)

cv2.minEnclosingCircle() returns the minimal circle (it returns the center and radius) enclosing all the points of the contour:

(x, y), radius = cv2.minEnclosingCircle(contours[0])

cv2.fitEllipse() returns the ellipse that fits (with the minimum least square errors) all the points of the contour:

ellipse = cv2.fitEllipse(contours[0])

cv2.approxPolyDP() returns a contour approximation of the given contour, based on the given precision. This function uses the Douglas-Peucker algorithm.

The epsilon parameter establishes the precision, determining the maximum distance between the original curve and its approximation. Therefore, the resulting contour is a decimated contour similar to the given contour with fewer points:

approx = cv2.approxPolyDP(contours[0], epsilon, True)

extreme_points() calculates the four extreme points defining a given contour:

def extreme_points(contour):
    """Returns extreme points of the contour"""

    index_min_x = contour[:, :, 0].argmin()
    index_min_y = contour[:, :, 1].argmin()
    index_max_x = contour[:, :, 0].argmax()
    index_max_y = contour[:, :, 1].argmax()

    extreme_left = tuple(contour[index_min_x][0])
    extreme_right = tuple(contour[index_max_x][0])
    extreme_top = tuple(contour[index_min_y][0])
    extreme_bottom = tuple(contour[index_max_y][0])

    return extreme_left, extreme_right, extreme_top, extreme_bottom

np.argmin() returns the indices of the minimum values along an axis. The indices corresponding to the first occurrence are returned in the case of multiple occurrences of the minimum values. np.argmax() returns the indices of the maximum values. Once the indices are calculated (for example, index), we will get the corresponding component of the array (for example, contour[index]—[[ 40 320]]) and we access the first component (for example, contour[index][0]—[ 40 320]). Finally we convert it to a tuple (for example, tuple(contour[index][0])—(40,320)).

As you can see, you can perform these calculations in a more compact way:

index_min_x = contour[:, :, 0].argmin()
extreme_left = tuple(contour[index_min_x][0])

This code can be rewritten as follows:

extreme_left = tuple(contour[contour[:, :, 0].argmin()][0])