Hu moment invariants are invariant with respect to translation, scale, and rotation and all the moments (except the seventh one) are invariant to reflection. In the case of the seventh one, the sign has been changed by reflection, which enables it to distinguish mirror images. OpenCV provides cv2.HuMoments() to calculate the seven Hu moment invariants.
The signature for this method is as follows:
cv2.HuMoments(m[, hu]) → hu
Here, m corresponds to the moments calculated with cv2.moments(). The output hu corresponds to the seven Hu invariant moments.
The seven Hu moment invariants are defined as follows:
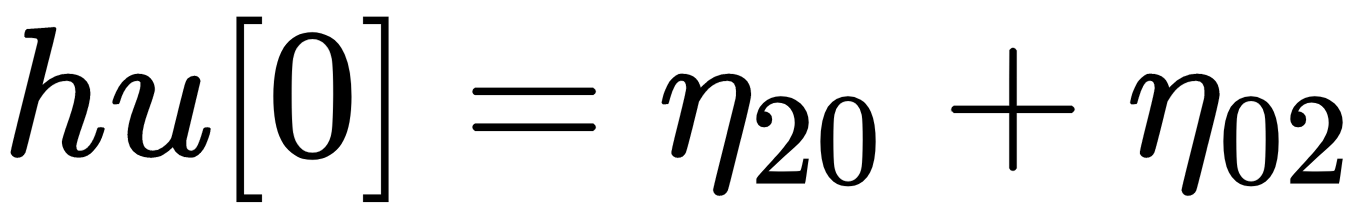
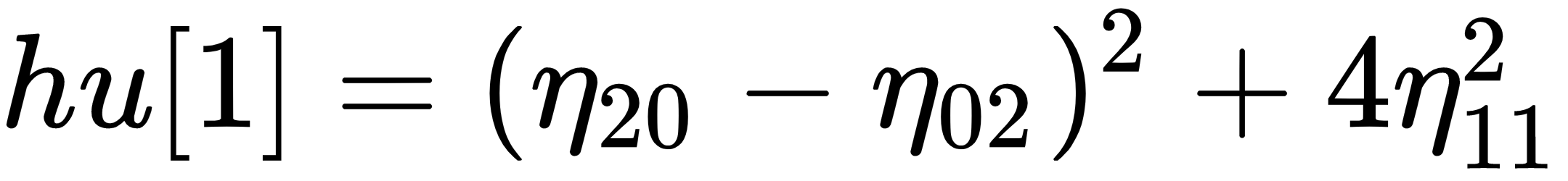
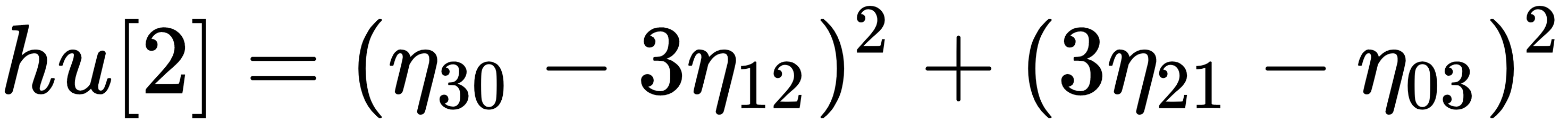
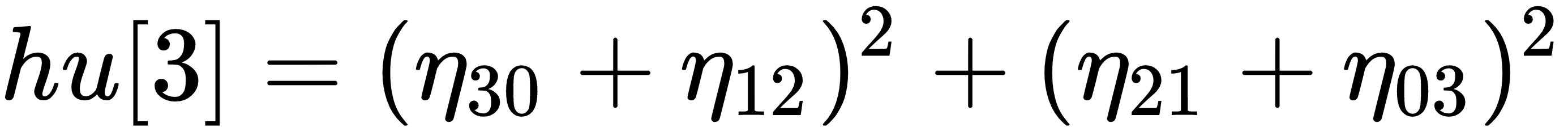
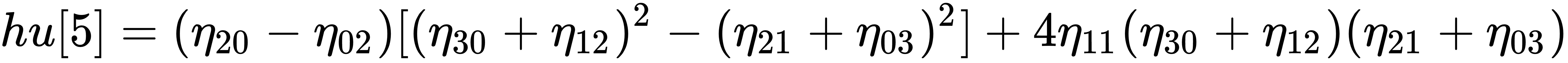
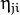stands for 
.
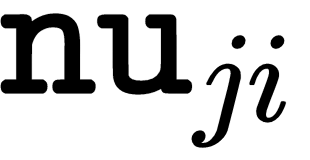In the contours_hu_moments.py script, the seven Hu moment invariants are calculated. As stated before, we must first calculate the moments by using cv2.moments(). In order to calculate the moments, the parameter can be both a vector shape and an image. Besides, if the binaryImage parameter is true (only used for images), all non-zero pixels in the input image will be treated as 1's. In this script, we calculate moments using both a vector shape and an image. Finally, with the calculated moments, we will compute the Hu moment invariants.
The key code is explained next. We first load the image, transform it to grayscale, and apply cv2.threshold() to get a binary image:
# Load the image and convert it to grayscale:
image = cv2.imread("shape_features.png")
gray_image = cv2.cvtColor(image, cv2.COLOR_BGR2GRAY)
# Apply cv2.threshold() to get a binary image
ret, thresh = cv2.threshold(gray_image, 70, 255, cv2.THRESH_BINARY)
At this point, we compute the moments by using the thresholded image. Afterward, the centroid is calculated and, finally, the Hu moment invariants are calculated:
# Compute moments:
M = cv2.moments(thresh, True)
print("moments: '{}'".format(M))
# Calculate the centroid of the contour based on moments:
x, y = centroid(M)
# Compute Hu moments:
HuM = cv2.HuMoments(M)
print("Hu moments: '{}'".format(HuM))
Now, we repeat the procedure, but in this case, the contour is passed instead of the binary image. Therefore, we first calculate the coordinates of the contour in the binary image:
# Find contours
contours, hierarchy = cv2.findContours(thresh, cv2.RETR_EXTERNAL, cv2.CHAIN_APPROX_NONE)
# Compute moments:
M2 = cv2.moments(contours[0])
print("moments: '{}'".format(M2))
# Calculate the centroid of the contour based on moments:
x2, y2 = centroid(M2)
# Compute Hu moments:
HuM2 = cv2.HuMoments(M2)
print("Hu moments: '{}'".format(HuM2))
Finally, the centroids are shown as follows:
print("('x','y'): ('{}','{}')".format(x, y))
print("('x2','y2'): ('{}','{}')".format(x2, y2))
As you can see, the computed moments, the Hu moment invariants, and the centroids are pretty similar but not the same. For example, the obtained centroids are as follows:
('x','y'): ('613','271')
('x2','y2'): ('613','270')
As you can see, the y coordinate differs by one pixel. The reason for this is limited raster resolution. The moments estimated for a contour are a little different from the moments calculated for the same rasterized contour. The output for this script can be seen in the next screenshot, where both centroids are shown in order to highlight this small difference in the y coordinate:
In contours_hu_moments_properties.py, we load three images. The first one is the original. The second one corresponds with the original but is rotated 180 degrees. The third one corresponds to a vertical reflection of the original. This can be seen in the output of the script. Additionally, we print the computed Hu moment invariants derived from the three aforementioned images.
The first step of this script is to load the images using cv2.imread() and convert them to grayscale by making use of cv2.cvtColor(). The second step is to apply cv2.threshold() to get the binary image. Finally, Hu moments are computed using cv2.HuMoments():
# Load the images (cv2.imread()) and convert them to grayscale (cv2.cvtColor()):
image_1 = cv2.imread("shape_features.png")
image_2 = cv2.imread("shape_features_rotation.png")
image_3 = cv2.imread("shape_features_reflection.png")
gray_image_1 = cv2.cvtColor(image_1, cv2.COLOR_BGR2GRAY)
gray_image_2 = cv2.cvtColor(image_2, cv2.COLOR_BGR2GRAY)
gray_image_3 = cv2.cvtColor(image_3, cv2.COLOR_BGR2GRAY)
# Apply cv2.threshold() to get a binary image:
ret_1, thresh_1 = cv2.threshold(gray_image_1, 70, 255, cv2.THRESH_BINARY)
ret_2, thresh_2 = cv2.threshold(gray_image_2, 70, 255, cv2.THRESH_BINARY)
ret_2, thresh_3 = cv2.threshold(gray_image_3, 70, 255, cv2.THRESH_BINARY)
# Compute Hu moments cv2.HuMoments():
HuM_1 = cv2.HuMoments(cv2.moments(thresh_1, True)).flatten()
HuM_2 = cv2.HuMoments(cv2.moments(thresh_2, True)).flatten()
HuM_3 = cv2.HuMoments(cv2.moments(thresh_3, True)).flatten()
# Show calculated Hu moments for the three images:
print("Hu moments (original): '{}'".format(HuM_1))
print("Hu moments (rotation): '{}'".format(HuM_2))
print("Hu moments (reflection): '{}'".format(HuM_3))
# Plot the images:
show_img_with_matplotlib(image_1, "original", 1)
show_img_with_matplotlib(image_2, "rotation", 2)
show_img_with_matplotlib(image_3, "reflection", 3)
# Show the Figure:
plt.show()
The computed Hue moment invariants are as follows:
Hu moments (original): '[ 1.92801772e-01 1.01173781e-02 5.70258405e-05 1.96536742e-06 2.46949980e-12 -1.88337981e-07 2.06595472e-11]'
Hu moments (rotation): '[ 1.92801772e-01 1.01173781e-02 5.70258405e-05 1.96536742e-06 2.46949980e-12 -1.88337981e-07 2.06595472e-11]'
Hu moments (reflection): '[ 1.92801772e-01 1.01173781e-02 5.70258405e-05 1.96536742e-06 2.46949980e-12 -1.88337981e-07 -2.06595472e-11]'
You can see that the computed Hu moment invariants are the same in the three cases, with the exception of the seventh one. This difference is highlighted in bold in the output shown previously. As you can see, the sign is changed.
The following screenshot shows the three images used to compute Hu moment invariants:
