
In this chapter, we’ll see a few ways you can eliminate bad answer choices, avoid traps, improve your odds of answering correctly if you have to guess, and maximize your Math score. We’ll also teach you how to best make use of your calculator, when it is permitted, and how to get along without it.
In the Reading section of this book, you learned about various ways to eliminate wrong answers on hard questions. Well, that idea comes into play on the SAT Math Test as well. This chapter provides an overview of the strategies you should know to maximize your Math score, as well as some tips on how to use your calculator wisely (and how to work without it!).
One way to eliminate answers on the Math Test is by looking for ones that are the wrong size, or that are not “in the ballpark.” We call this strategy Ballparking. Although you can use your calculator on the following question, you can also eliminate without doing any calculations.

25. 
Joy plants three rows of corn in her garden. The row on the south edge of the garden receives more sunlight than the row on the north edge of the garden. Therefore, the corn on the north edge of the garden is 30% shorter than that on the south. If the corn on the south edge of the garden is 50 inches tall, how tall is the corn on the north edge of the garden, in inches?
A) 30
B) 33
C) 35
D) 65
Here’s How to Crack It
The question states that the corn on the north edge is shorter than the corn on the south edge, which is 50 inches tall. You are asked to find the height of the corn on the north edge, so the correct answer must be less than 50. Eliminate (D), which is too high. Often, one or more of the bad answers on these questions is the result you would get if you applied the percentage to the wrong value. To find the right answer, take 30% of 50 by multiplying 0.3 by 50 to get 15, then subtract that from 50. The corn on the north edge would be 35 inches tall, which is (C).

You never know what a question is going to ask you to do, so make sure to always Read the Full Question before solving. Underline what you are actually solving for and any key words you think you might forget about as you solve the question. Then, try to Ballpark before you solve.

7. If 16x – 2 = 30, what is the value of 8x – 4 ?
A) 12
B) 15
C) 16
D) 28
Here’s How to Crack It
First, see if you can eliminate answers by Ballparking, which can also work on algebra questions. To go from 16x to 8x, you would just divide by 2. Dividing 30 by 2 gives you 15, so 28 is way too big. Eliminate it. The correct answer is not likely to be 15, either, because that ignores the –2 and the –4 in the question.
To solve this one, add 2 to each side of the equation to get 16x = 32. Divide both sides by 2, which gives you 8x = 16. But don’t stop there! The full question asks for 8x – 4, so (C) is a trap answer. You have to take the last step and subtract 4 from both sides to find that 8x – 4 = 12, which is (A).

When dealing with complicated math problems, take it one little piece at a time. We call this strategy Bite-Sized Pieces. If you try to do more than one step at a time, especially if you do it in your head, you are likely to make mistakes or fall for trap answers. After each step take a look at the answer choices and determine whether you can eliminate any.
Try the following question.

9. A paper airplane is thrown from the top of a hill and travels horizontally at 9 feet per second. If the plane descends 1 foot for every 3 feet travelled horizontally, how many feet has the plane descended after 5 seconds of travel?
A) 3
B) 10
C) 15
D) 20
Here’s How to Crack It
There are a few things going on here. The plane is traveling horizontally, and it is also descending. Start by figuring out how far it travels horizontally. It moves in that direction at 9 feet per second for 5 seconds, so it moves horizontally 9 × 5 = 45 feet. It descends 1 foot for every 3 traveled horizontally. If it goes 45 feet horizontally, it will descend more than 3 feet, so eliminate (A). Now figure out how many “3 feet” are in 45 feet—for each one of them, the plane will descend 1 foot. 45 ÷ 3 = 15, so the plane descends 15 feet, (C).
You may also have noticed that all the numbers in the question are odd. This makes it unlikely that the answer would be 10 or 20, which are even. If you see things like that, use them as opportunities to eliminate.

Here’s another example.

6.
(5jk2 + 5j2 – 2j2k) – (jk2 + 2j2k + 5j2)
Which of the following is equivalent to the expression above?
A) 4jk2
B) 4jk2 – 4j2k
C) 5j2k4 – 10j4k
D) 8j2k3 + 7j2k – 5j2
Here’s How to Crack It
Start with one tiny piece of this ugly-looking question. The first set of parentheses starts with a term containing jk2. Check in the second set of parentheses for the same combination of variables and exponents. The first term there matches, so the first step to take is 5jk2 – jk2 = 4jk2. There are no other terms with jk2, so the correct answer must contain 4jk2. Eliminate (C) and (D). Now you have a fifty-fifty chance of getting it right, so you can guess and go, or you can do one more step to determine if the answer is (A) or (B). The difference between the two answers is the – 4j2k term, so focus on the terms in the expression that contain j2k. In the first set of parentheses, you have –2j2k, and then you subtract the 2j2k term in the second set of parentheses. –2j2k – 2j2k = –4j2k, so the correct answer is (B).

As you solve questions in small pieces, write down the steps. Don’t keep track of things in your head—your test booklet is there for your notes. If a figure is given, write the information from the question right on it.
Here’s an example.

12.
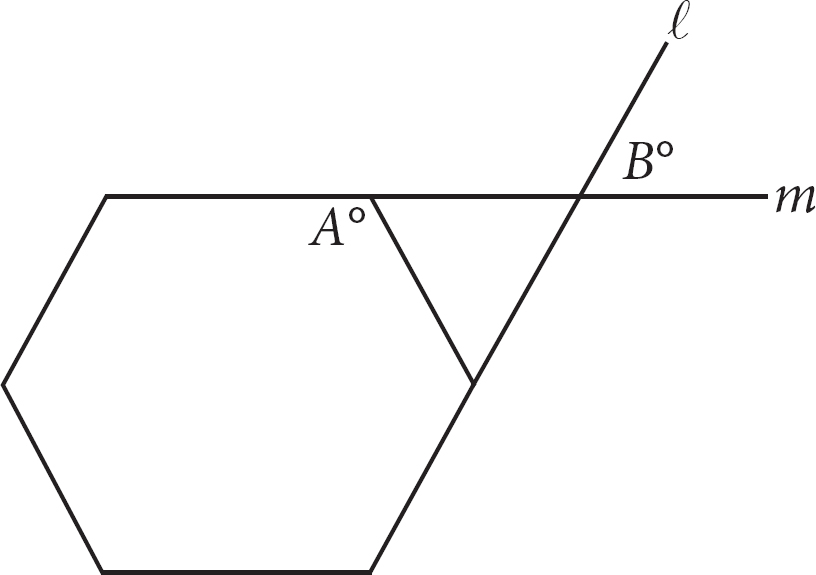
Lines l and m extend from two sides of the regular hexagon as shown above. If A = 120, what is the value of B, in degrees?
A) 30
B) 60
C) 90
D) 140
Here’s How to Crack It
Sometimes Ballparking can even help on geometry questions. Not all pictures are drawn to scale, so don’t assume the figure is exact. You can, however, use what the question tells you about the figure to estimate angles, line lengths, areas, and points on graphs in the xy-plane.
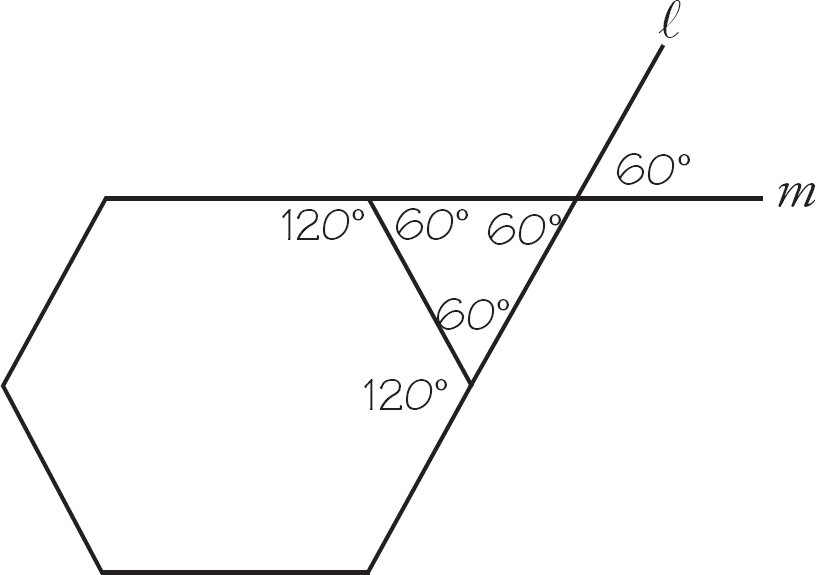
If the previous figure is drawn to scale, the angle with measurement B appears to be acute, making (A) or (B) a good bet. The question says the hexagon is “regular,” which means that all the interior angles have the same measure, and the drawing looks like this is the case. Start by marking the angle that is A° as 120° on the figure. This angle looks like 120°, so B can’t possibly equal 90° or 140°. Eliminate (C) and (D). To find the exact value of B, you need to find the measure of the angle opposite it, which is one of the angles from the triangle. The angle of the upper-left corner of the triangle is formed by drawing a straight line from the angle that is A°, or 120°. There are 180° in a straight line, so the upper-left corner of the triangle measures 180° – 120° = 60°. Label this measure on the figure as well. The fact that the hexagon is regular means that all the interior angles are 120°, so label the angle next to the bottom corner of the triangle. Since this corner of the triangle is formed in the same way as the upper-left corner, the bottom corner also measures 60°. Label it. There are 180° in a triangle, so the upper-right angle is also 60°. The angle measuring B° is opposite this, so B is 60° and (B) is correct.
By the time you’re done, your figure should look like this:

As you already know, the Math Test is divided into a shorter section in which calculator use is not permitted (Section 3) and a longer section in which it is permitted (Section 4). This affects the way you do the questions in each of these sections. The No Calculator section will lean more toward fluency and understanding of mathematical concepts, but that doesn’t mean you won’t have to calculate anything. On the Calculator section, using the calculator is not always helpful. In this book, if you see a calculator symbol next to a question, it means you may use your calculator as needed to arrive at the answer. If there is no calculator symbol next to a question, leave that calculator alone! The rest of this chapter will give you general information about how to use your calculator when you can and what to do when you can’t. Other Math chapters will provide information about using your calculator in specific situations. Even if you now use a calculator regularly in your math class at school, you should still read this chapter and the other Math chapters carefully and practice the techniques we describe.
ETS and the College Board say that the purpose of the No Calculator section is to test your “fluency” and “conceptual understanding” of math topics. While you may have to rearrange some terms and do some manipulation to answer questions correctly, you won’t be expected to do anything too crazy, like calculate  to three decimal places—so have no fear!
to three decimal places—so have no fear!
You’ll need to take your own calculator to the testing center. Make sure that your calculator is either a scientific or a graphing calculator and can perform the order of operations correctly. To test your calculator, try the following problem, typing it in exactly as written without hitting the ENTER or “=” key until the end: 3 + 4 × 6 = . The calculator should give you 27. If it gives you 42, it’s not a good calculator to use.
A calculator can be an obstacle at times. The test writers have designed this section of the test in the hopes of assessing your “appropriate use of tools,” and they freely admit that a calculator can slow you down on some of the questions. So, by all means, use that calculator if you need it to avoid making careless errors, but don’t forget that using your brain and pencil can be a faster way to get to the right answer.
Many students already own a graphing calculator. If you have one, great; if you don’t, don’t sweat it. A graphing calculator is not necessary for the SAT, though it may help simplify certain graphing problems.
If you do decide to use a graphing calculator, keep in mind that it cannot have a QWERTY-style keyboard (like the TI-95). Most of the graphing calculators have typing capabilities, but because they don’t have typewriter-style keyboards, they are perfectly legal.
Also, you cannot use the calculator on your phone. In fact, on test day, you will have to turn your phone off and put it underneath your seat.
The only danger in using a calculator on the SAT is that you may be tempted to use it in situations in which it won’t help you. Some students believe that their calculator will solve many difficulties they have with math. It won’t. This type of thinking may even occasionally cause students to miss a problem they might have otherwise answered correctly on their own. Remember that your calculator is only as smart as you are. But if you practice and use a little caution, you will find that your calculator will help you a great deal.
Here is a complete list of what a calculator is good at on the SAT:
arithmetic
decimals
fractions
square roots
percentages
graphs (if it is a graphing calculator)
We’ll discuss the calculator’s role in most of these areas in the next few chapters.
Adding, subtracting, multiplying, and dividing integers and decimals is easy on a calculator. But, you need to be careful when you key in the numbers. A calculator will only give you an incorrect answer to an arithmetic calculation if you press the wrong keys.
The main thing to remember about a calculator is that it can’t help you find the answer to a question you don’t understand. If you wouldn’t know how to solve a particular problem using pencil and paper, you won’t know how to solve it using a calculator either. Your calculator will help you, but it won’t take the place of a solid understanding of basic SAT mathematics.
Whether or not calculator use is permitted, the first step should be to set up the problem or equation on paper; this will keep you from getting lost or confused. This is especially important when solving the problem involves a number of separate steps. The basic idea is to use the extra space in your test booklet to make a plan, and then use your calculator to execute it.
Working on scratch paper first will also give you a record of what you have done if you change your mind, run into trouble, or lose your place. If you suddenly find that you need to try a different approach to a problem, you may not have to go all the way back to the beginning. This will also make it easier for you to check your work, if you have time to do so.
Don’t use the memory function on your calculator (if it has one). Because you can use your test booklet as scratch paper, you don’t need to juggle numbers within the calculator itself. Instead of storing the result of a calculation in the calculator, write it on your scratch paper, clear your calculator, and move to the next step of the problem. A calculator’s memory is fleeting; scratch paper is forever.
In the next chapter, we will discuss the proper order of operations when solving equations that require several operations to be performed. Be sure you understand this information, because it applies to calculators as much as it does to pencil-and-paper computations. You may remember PEMDAS from school. PEMDAS is the order of operations. You’ll learn more about it and see how questions on the SAT require you to know the order of operations. You must always perform calculations in the proper order.
Most scientific calculators have buttons that will automatically simplify fractions or convert fractions from decimals. (For instance, on the TI-81, TI-83, and TI-84, hitting “Math” and then selecting the first option, “Answer → Fraction,” will give you the last answer calculated as a fraction in the lowest terms.) Find out if your calculator has this function! If it does, you can use it to simplify messy fractions on the Calculator section. This function is also very useful when you get an answer as a decimal, but the answer choices given are all fractions. For the No Calculator section, you will have to be able to do these things by hand, so practice these skills in the next chapter. (For Grid-In questions, it is not necessary to reduce a fraction to its simplest form if it fits in the grid, and the decimal equivalent will also be accepted as a correct answer.)
Change the batteries on your calculator a week before the SAT so that you know your calculator won’t run out of power halfway through the test. You can also bring extra batteries with you, just in case. Although it isn’t very likely that the batteries will run out on your calculator on the day of the test, it could happen—so you want to be prepared.
Remember that the test writers are trying to test your ability to use your calculator wisely. As such, they have purposely created many questions in which the calculator is worthless. (There are questions that are so wordy and deceptive that reading carefully is a much more important skill than properly using a calculator.) So be sure to Read the Full Question—there may be some serious surprises in there. Finally, remember that on Section 3 you won’t be able to use it at all. Practice your math skills so that you can solve questions with or without your calculator.
Look for ways to eliminate answer choices that are too big or too small. Ballparking can help you find the right answer without extensive paper-and-pencil calculations when calculator use is not allowed. Even when you can use your calculator, Ballparking can help you avoid trap answers and improve your chances of getting the question right if you have to guess.
When Ballparking answers on geometry questions, use a bit of caution. The figures are not always drawn to scale. Use the given information to determine if you can trust your figure before using it to eliminate answers.
After you’ve set up the problem on the page, you should definitely use the calculator when allowed to avoid careless mistakes from doing math in your head.
Take your own calculator when you take the test. You don’t need a fancy one. Make sure your calculator doesn’t beep or have a typewriter-style keyboard.
Even if you already use a calculator regularly, you should still practice with it before the test.
Be careful when you key in numbers on your calculator. Check each number on the display as you key it in. Clear your work after you finish each problem or after each separate step.
A calculator can’t help you find the answer to a question you don’t understand. (It’s only as smart as you are!) Be sure to use your calculator as a tool, not a crutch.
Set up the problem or equation on paper first. By doing so, you will eliminate the possibility of getting lost or confused.
Don’t use the memory function on your calculator (if it has one). Scratch paper works better.
Whether you are using your calculator or paper and pencil, you must always perform calculations in the proper order.
If your calculator runs on batteries, make sure it has fresh ones at test time! Change them a week before.
Make sure your math skills are solid so you can tackle questions in the No Calculator section with confidence.