Mathématique :

Il y avait trois issues : la première en haut, à gauche, en regardant vers le bas, face au tableau noir. C’était l’entrée principale de l’amphithéâtre (« amphi » disait-on), la porte où se pressaient, bien avant l’heure du cours (huit heures, huit heures et demie ; il faisait nuit encore ; hiver donc, dehors noir ; sans détails, noir), les étudiants cherchant à s’assurer les meilleures places (celles où non seulement on était assis, mais où on entendait distinctement la voix du professeur : un luxe). Devant la porte se tenaient les distributeurs de tracts, les « politiques », du moins quand ils réussissaient à échapper à la vigilance de l’administrateur de l’institut (→ § 10) qui sans cesse essayait de les refouler jusque dans la rue, devant la grille rue Pierre-et-Marie-Curie ou, à défaut, devant l’entrée principale, sur les marches du perron. Ils s’obstinaient, conscients de l’importance planétaire de leur lutte.

J’arrivais tôt (j’arrive toujours tôt), et je m’asseyais presque en haut de l’« amphi », à peu près au niveau de la porte, dans la partie « montagne » de cette assemblée (pour employer le vocabulaire politique de 1793), de cette fausse Convention dont les étudiants supposés studieux, ceux qui se plaçaient aux premiers rangs, constituaient le « marais ». Je m’installais de préférence au fond de la rangée, sur le banc étroit et inconfortable, où je n’avais qu’un voisin de droite, où mon voisin de gauche n’était pas le mur, comme plus bas dans les gradins, mais un bord, une paroi vitrée.

L’amphi se remplissait, le bruit des conversations faisait peu à peu place à celui des papiers, au grincement de la craie sur le tableau, là-bas, et à travers la buée des respirations je voyais, derrière le verre sale, la nuit presque attentive, proche, lentement s’évaporer en froideur humide pour faire place à un jour pâle, et triste.

Entre le début et la fin du cours l’obscurité nocturne abandonnait la ville pour faire place à une pénombre grise, hivernale. Mais au moment où je venais m’asseoir, prendre ma place inconfortable, étroite, au sein de ce volume universitaire aux tranches trapézoïdales (un trapèze rectangle inversé, à la base tournée vers le ciel), encore presque vide, quand la vitre était encore nue de la buée des respirations, je me voyais, en regardant vers le dehors, presque au-dehors moi-même, immédiatement adjacent à la nuit, contigu à sa masse toujours impénétrable et bleue, sombre.

Le jour, au-dehors, naissait lentement, médiocrement, pénétrait avec peine, insuffisamment, le ronronnement studieux, triomphait difficilement de l’insuffisante lumière électrique, froide. C’était au milieu de difficiles années, pendant l’année universitaire 1954-1955 ; lieu : l’institut Henri-Poincaré – amphithéâtre Hermite ; rubrique : certificat de Calcul différentiel et intégral (CDI) – M. G(ustave) Choquet, professeur.

Je me tournais, je voyais mon image se former quelque part en l’air extérieur, conformément aux règles les plus banales et les mieux assurées de l’optique géométrique (certificat de Physique générale), puis se couvrir de buée, puis devenir imprécise, s’affaiblir, disparaître. Il faisait nuit, et c’était l’hiver. Il faisait froid ; froid dehors, froid dans l’amphi mal chauffé. J’appuyais ma main sur le verre nu, je le pressais de la paume, pour effacer la buée, pour mieux distinguer mon image, celle de mes voisins et voisines studieux, et surtout m’ébahir, engourdi, de la qualité énigmatique de cette lumière paradoxale baignant des visages suspendus en l’air extérieur, sans support, lumière jaune électrique & virtuelle, illuminant comme une poche d’espace gelé, creusée dans la nuit inflexible.

C’est dire que j’écoutais distraitement, notant paresseusement sur mon cahier, en bribes quasi illisibles, quelque définition d’al lure pas trop inquiétante, ou le corollaire évident d’un théorème restant, lui, entièrement mystérieux. Encore fallait-il que les énoncés laissent une trace déchiffrable sur le tableau.

Mais « Choquet » – on disait « Choquet », comme on disait « Schwartz », ou « Bouligand », avec ces guillemets oraux implicites qui sont moins une marque de familiarité désinvolte qu’une désignation citationnelle, une individuation apparente mais en fait impersonnelle de la « fonction professeur », qui ne se colorait que secondairement, à mesure que l’« année » avançait, que s’approchait le mois des examens (juin), d’un halo réactionnel collectif, de rejet ou d’adhésion, d’inquiétudes et d’anecdotes, lesquelles, triées, épurées, compliquées et déformées, ainsi qu’il convient à une tradition orale, se transmettraient aux populations d’étudiants de l’année suivante pour constituer peu à peu la légende professionnelle des noms, devenus « portraits », en ce sens très singulier, de leurs porteurs – « Choquet », disais-je, écrivait peu sur le tableau. Il parlait sa mathématique, sans notes, parfois dessinant en l’air avec les mains, gestes de géomètre.

Les mathématiciens, dans la représentation ordinaire qu’en ont les gens, celle qui surgit spontanément quand on rencontre quelqu’un qui ne vous connaît pas et qui apprend que vous êtes quelqu’un qui « fait des mathématiques » (elle se révèle immédiatement après la phrase rituelle : « au lycée (ou “à l’école”), moi, j’étais nul en maths »), s’expriment dans une langue pour presque tous incompréhensible, donc prestigieuse, offrant des vérités à la fois capitales et indéchiffrables. La réaction de la population de l’amphi du CDI de 1954 aux premières paroles de Choquet, qui s’expliquait pour la première fois dans ce rôle (dans cette capacité) en ces lieux (il venait de prendre la succession d’un des derniers représentants de l’école ancienne d’analyse « à la française », « Valiron »), fut étonnamment semblable à la réaction courante des non-mathématiciens : l’effarement. Quel que fût leur « passé » mathématique, ils ne s’étaient pas attendus à cela.

2 Il y a quelques années nous avions, mon ami Pierre Lusson et moi-même,

Il y a quelques années (au milieu des années quatre-vingt) nous avions, mon ami Pierre Lusson et moi-même, au département de mathématiques de l’université Paris-X (Nanterre), une très jolie jeune collègue, une ATER (assistante transitoire d’enseignement et de recherche, si je ne m’abuse (mais je m’abuse peut-être : déjà ces noms, ces sigles, ces images d’un passé pourtant encore si récent se couvrent de buée (d’ailleurs toutes les images, tous les souvenirs, dès qu’on souffle dessus pour les réchauffer, se couvrent de telles buées, s’affaiblissent, pénétrés partout d’imprécision))). Et un lundi matin, comme nous étions ensemble dans le minuscule bureau de notre « département », voyant Sonia bâiller légèrement en sortant la feuille d’exercices de logique de son cartable (cartable, dis-je ; non « serviette » ; je ne devrais pas : le mot cartable est certainement lui-même un mot préhistorique), Pierre lui dit (en substance) : « On danse le week-end, et le lundi on bâille ! » Elle en convint. On bavarda sur ce thème un moment.

Et Pierre, encouragé par ce premier succès conversationnel (il était, il est, comme « l’enfant d’éléphant » de Kipling, plein d’une « insatiable curiosité »), heureux par ailleurs de pouvoir utiliser, grâce aux renseignements fournis par Juliette et Cécile, ses filles, un vocabulaire adéquat à la circonstance, posa à Sonia une autre question : « Et quand vous allez danser “en boîte” est-ce que vous leur dites, à vos danseurs, que vous êtes mathématicienne ? » La réponse de Sonia fut immédiate : « Ah non ! je l’ai fait une fois, mais je n’ai jamais recommencé ! »

Car, devant la Mathématique, incarnée de manière si inattendue, si imprévisible, si brusque, non par le visage traditionnellement peu amène d’un ancien instituteur ou professeur, ou la caricature du savant fou de l’opinion commune, mais par une jeune fille, et qui plus est aussi jolie que Sonia, le réflexe spontané du danseur avait été la fuite.

Ainsi, face à la brusque métamorphose de l’objet mathématique qui s’opérait devant leurs yeux (devant leurs oreilles surtout), les étudiants les plus aguerris, anciens des classes préparatoires ou rescapés de l’hécatombe des deux sessions d’examen du certificat de Mathématiques générales, avaient senti vaciller leurs certitudes les mieux établies : ils s’étaient fait de la mathématique, au cours de leurs précédentes études, une représentation devenue peu à peu invariable, ronronnante et stable, et voilà qu’elle changeait tellement qu’elle se refermait, hermétiquement, devant eux. Et ce nouveau visage, ils ne le trouvaient généralement pas joli.

Le désarroi des redoublants était le plus palpable : entre les cours de « Valiron » de l’année précédente et ceux de « Choquet » ils ne découvraient pour ainsi dire aucun point commun ; comme si, pendant les vacances universitaires, cette science avait été remplacée par une autre, qui n’eût porté que par commodité le même nom.

Certains, tel le danseur de Sonia, s’enfuirent, changèrent définitivement d’orientation. Quelques-uns trouvèrent cette péripétie sévère mais drôle, puis, somme toute, séduisante. La plupart entreprirent seulement d’apprendre (éventuellement de comprendre) ce qu’on leur exposait. Voilà, n’est-ce pas, le vrai « incontournable », la banalité même de l’enseignement : écouter (lire), retenir, restituer, tout cela sans trop réfléchir. Il s’agissait, cependant, d’une situation exceptionnelle. Tous en étaient conscients. Une rupture avait eu lieu, une tradition devenue routine avait succombé, et quelque chose d’autre commençait là (ils en étaient les témoins involontaires), avec ostentation, avec désinvolture. « Choquet », c’était clair, semblait s’amuser de leur, de notre désarroi. Du passé (mathématique) on avait fait, apparemment, table rase (→ § 11).

Vu depuis la porte, dans le mouvement du regard, comme je le fais au souvenir en ce moment, le rectangle des bancs, des tables, des gradins semblait une page, abondamment ponctuée de signes d’attention ; avec, pour « en-tête », le tableau devant lequel parlait, debout, le professeur (les mathématiciens, à la différence des « littéraires », parlent toujours debout). Dès avant l’heure, l’amphi était plein. La nouveauté intimidante du contenu, l’absence de manuels (le précédent titulaire de la chaire, le professeur Valiron, avait écrit un livre, que tous les étudiants possédaient et dont, semble-t-il, les dernières années de son enseignement, il se bornait à commenter au tableau, obscurément, quelques chapitres) rendaient l’assistance aux cours presque obligatoire.

En ce temps-là le professeur ne pénétrait pas dans la salle de cours par la même entrée que les étudiants. Une autre porte s’ouvrait en bas, à la droite de l’immense tableau à trois éléments articulés prêts à glisser les uns sur les autres à volonté, sauf panne ou fausses manœuvres, commandés par un autre tableau, un tableau de bord électrique situé sous la longue table qui le séparait des premiers bancs. (À moins qu’il n’ait été placé au bas du tableau noir même ; ou sur les côtés ; en fait, je n’en sais rien : il suffit que je pense à une quelconque de ces possibilités pour aussitôt la voir !)

(Je regarde depuis le haut de l’amphithéâtre, debout ; je le vois s’étendre au-dessous de moi, à moitié plein ; l’heure du commencement du cours s’approche. Le monde d’où surgit cette image du passé vient juste de naître, et il cessera avec elle, c’est-à-dire immédiatement après ces mots, et qui plus est presque instantanément. Je vois la surface lisse et noire du tableau, couverte à gauche d’un nuage de poussière fine de craie, la trace d’un effacement ; et d’un dessin, constitué de deux ovales peu réguliers, des « patatoïdes » pourrait-on dire, empiétant l’un sur l’autre, s’intersectant, leur partie commune hachurée. L’intensité, la proximité physique de cette surface noire, de ce dessin, sont des traits essentiels de ce souvenir : ils sont si proches, si nets à mon regard qu’ils ne peuvent que montrer un réel, qu’avoir été.)

3 Derrière cette porte se trouvait un espace protégé,

Derrière cette porte d’en bas se trouvait un espace protégé, un sanctuaire professoral : pas un bureau mais une salle de cours en miniature, avec tableau, table, chaise, de la craie, encore de la craie, toujours de la craie. On n’y pénétrait pas sans autorisation expresse, pour poser une question, demander un éclaircissement, un conseil.

Le cérémonial d’entrée du professeur, même s’il était loin de la pompe qui régnait alors à la Sorbonne (comme dans l’amphi Richelieu, au nom prédestiné, où j’avais suivi une ou deux fois les cours de Linguistique générale du professeur Martinet), symbolisée non seulement par l’antiquité chargée d’ombres vénérables du décor mais par la présence d’un appariteur (je ne parle pas du Collège de France, où la parution-apparition en scène du maître est encore aujourd’hui solennellement annoncée), maintenait une distance sévère entre les deux pôles de la relation de communication « aurale » du savoir, entre émetteur (le professeur) et récepteurs (les étudiants : nous, moi). Il m’a fallu plusieurs mois avant d’oser franchir une première fois cette porte d’en bas. Cela ne m’est pas arrivé souvent.

Beaucoup plus tard, dans les années soixante-dix surtout, pendant le long crépuscule de l’IHP (prononcer <Iächepé>, nom familier de l’institut Henri-Poincaré), qu’avaient déserté d’abord les étudiants, devenus trop nombreux et surtout dispersés après la tourmente soixante-huitarde dans les nouvelles universités issues, par multiplication cellulaire, de l’unique et obèse Université de Paris, puis peu à peu presque dessaisi de toutes activités proprement mathématiques (revenues en partie il y a quelques années), mais que quelques-uns ne se résignaient pas à abandonner tout à fait aux physiciens, y maintenant, combat d’arrière-garde, des « séminaires », s’y retrouvant à petits groupes pour travailler devant un tableau noir (les couloirs, les salles presque déserts maintenant), je suis souvent revenu, quasi clandestinement, dans ce petit bureau.

En mai ou juin, l’année universitaire finissante laissait assez de temps pour ces flâneries mi-studieuses mi-nostalgiques, et j’y donnais rendez-vous de travail, les samedis matin, quand les deux amphis (Darboux et Hermite), et la « salle U ou V » de la rue d’Ulm (désignation proprement « heisenbergienne »), qui auraient été mes premiers choix, étaient, par extraordinaire, occupés, à mon « élève » (« Bonnin », de Dijon), et à « l’élève, (“Pallo”), de mon élève (“Bonnin” »), pour de longues séances de « calculs de parenthèses » (aux dispositions traduites, cabalistiquement pour le profane, en « notation polonaise », ces longues séquences que nous bâtissions sur les toujours deux mêmes symboles : des « alphas » et des points : « alpha point alpha point alpha alpha point point point », par exemple (→ § 12)).

La matinée avançait, il faisait chaud. J’ouvrais la petite fenêtre aux vitres dépolies donnant sur l’allée qui s’enfuit au pied du bâtiment vers un portail situé entre l’Institut de Géographie et l’Institut océanographique ; et de l’autre côté de l’allée, entre l’allée et la rue, le soleil pointillait le fouillis végétal de ses propres séquences, bien plus incompréhensibles, variées et enchevêtrées que les nôtres.

Sur cette allée s’ouvrait la troisième issue de l’amphi : une autre porte, tout en bas, à gauche cette fois du tableau (→ § 13). Mais elle ne s’ouvrait que de l’intérieur. Aussi, en cas de retard, quand on se hâtait depuis le carrefour de la rue Saint-Jacques et de la rue Gay-Lussac, sur le sentier hivernal mal éclairé bordé de longues silhouettes noires d’arbres nus et de mystérieux laboratoires en briques qui auraient été toulousainement rose-rouge sans l’obscurité et la suie, on ne pouvait pas pénétrer par là dans l’amphithéâtre. Il fallait faire tout le tour du bâtiment, d’un côté ou de l’autre, soit vers les marches du perron et le couloir central, soit, retournant en arrière, rejoindre, par un escalier extérieur en ciment, un autre couloir, orthogonal au premier, confluant avec le premier devant la première porte, et qui passait le long de la « Salle des étudiants ».

C’est par cette troisième issue que s’écoulait, abasourdi, le flot des auditeurs des premiers rangs, dès que le silence professoral s’était fait. Ils s’en allaient vers les cafés, les bibliothèques, (« Sainte-Geneviève », « la Sorbonne »), vers le métro, vers le jardin du Luxembourg (le « Luco »), vers d’autres cours, vers l’École normale supérieure toute proche, rue d’Ulm (pour ceux des « normaliens » et de leurs dépendants intellectuels ou sentimentaux qui daignaient faire l’effort de se traîner jusque-là, dans des lieux aussi peu dignes de leur rang. Ils y venaient en fait relativement nombreux cette année-là écouter « Choquet » qui n’était pas considéré comme indigne de leur auguste présence. Mais pour rétablir l’équilibre sans doute, après ce compromis et cette promiscuité, certains d’entre eux tenaient à manifester leur condescendance en agitant quelques rangs par des bavardages locaux à voix mi-basse, d’autres en se signalant par la singularité de leur tenue vestimentaire, comme « Douady » qui apparaissait parfois au milieu d’un cours, pieds nus, en pyjama).

En ce temps-là, on ne s’interdisait certes pas les murmures, ni même, parfois, les chahuts, qui sont aussi vieux que les universités ; ni les allées et venues dans les régions hautes de l’amphithéâtre, du côté de la porte d’entrée. Mais ce n’étaient là que des agitations collectives, impersonnelles, d’une masse de têtes indifférenciées. Nul ne faisait entendre, seul, sa voix, sa propre voix.Et surtout, nul n’interrompait le déroulement didactique de la parole professorale pour poser, publiquement, une question : l’expression d’un doute ou, pis, la dénonciation d’une erreur.

Telle était la règle générale, dans les cours de sciences du moins. Mais cet hiver-là l’auditoire restait, de bout en bout de l’heure, sinon attentif, du moins particulièrement silencieux. Les mouches proverbiales qui, si on en croit notre vieux « langage cuit », fréquentent volontiers les salles de conférences auraient même pu, parfois, faire entendre dans l’amphi Hermite le battement de leurs ailes en vol. Et je veux insister sur ceci : que ces silences avaient une densité et une tonalité particulières. Ils n’étaient indice ni d’émotion, ni d’enchantement, ni seulement de concentration appliquée. Ils marquaient avant tout la perplexité, ou même la stupéfaction. Je partageais cette stupéfaction.

4 Ce livre ne justifiera sans doute que faiblement la provocation de son titre

Ce livre ne justifiera sans doute que faiblement la provocation de son titre. Je dois le dire avant d’aller plus loin. Il serait non seulement malhonnête mais absurde de laisser croire le contraire. Notre antique, vénérable et toujours jeune aïeule, La Mathématique, née, dit-on, il y a vingt-six ou vingt-sept siècles sur les bords de la mer Égée ne trouvera pas en ces pages un monument de papier digne d’elle. Il est vrai qu’elle n’en a guère besoin.

L’auteur du livre (celui qui, ici, dit « je ») est (a été, plutôt) ce qu’on appelle un mathématicien. Il a (c’est de moi que je parle) consacré de très nombreuses heures à étudier, à enseigner, gravissant avec lenteur quelques échelons de l’échelle enseignante dans l’université, de simple assistant à maître-assistant à maître de conférences à professeur sans chaire (désignations aujourd’hui caduques ou ayant changé d’affectation) à professeur (mais pas au plus haut degré de l’échelle), à essayer d’augmenter la somme d’idées et de résultats qui constituent la (ou les) mathématique(s), mais ne contribuant en fait que d’une façon très obscure à son avancement. J’ai été un parmi beaucoup, un quelconque parmi ceux, très nombreux, de plus en plus nombreux, qui s’efforcent (l’immense majorité n’y parvenant que de manière négligeable) sans cesse de modifier, redessiner son visage. S’il s’agissait de dresser un monument à cette science, je ne serais donc pas, loin de là, le mieux qualifié pour le faire.

Mais il est vrai aussi que le titre de cet ouvrage ne saurait être un autre. La mathématique, au moins l’idée de mathématique, plutôt que la masse impossible à saisir dans sa totalité de ce qui la constitue (ou, plus restrictivement et plus exactement, la constituait comme science (ses branches, ses concepts, ses théorèmes) pour quelqu’un, et pour moi dans les années de mon immersion la plus entière dans son labyrinthe), la Mathématique est bien ce qui donne à mon livre son impulsion, son départ, son impetus et, symétriquement, mène à sa fin projetée, à son aboutissement, à l’élucidation du sens même de son existence, à la réponse, non, à une réponse à la question que pose tout livre : pourquoi ?

Mais ce n’est là, au fond, qu’une instance particulière du rapport qui unit un livre et son titre, que j’énoncerai sous la forme d’un axiome, emprunté à Gertrude Stein :

axiome Un titre est le nom propre d’un livre.

Et le livre alors n’est pas autre chose que ce qui répond (tente de répondre) à la question : pourquoi ce titre-là ? cas particulier à son tour, sous l’éclairage de l’axiome ci-dessus, de la question (de l’énigme si l’on veut) du nom propre : qu’est-ce qui unit un nom propre au « singulier », au singulier absolu, irréductible et rigide dont il est le nom ? Je le dis encore autrement : un livre est l’autobiographie de son titre et, comme tel, la narration d’une singularité (→ § 14). Les deux points qui suivent le mot « mathématique » dans le titre que j’ai choisi pour cette branche de mon ouvrage (une continuité-discontinuité de prose qui excède les pages que vous lisez ici) sont placés là dans cette intention.

J’ouvre ma fenêtre à l’air, pour quelques moments encore, nocturne ; une heure entre nuit et jour : entre quatre et cinq heures (solaires) ; un début de mai, rue d’Amsterdam, dans le neuvième arrondissement de Paris. L’air du dehors (de la cour) est froid, le bleu sombre du ciel se dilue, s’atténue. J’ai attendu plus de trente-sept ans pour oser m’arrêter, fixer délibérément cette image, cette poignée d’images : de tableau, de bancs, de têtes, de dessins à la craie, chargée de sens. Je la sors de son enfer, ou de ses limbes. Je la sors de mon souvenir pour l’effacer, comme tous les souvenirs que je fixe, en les écrivant, comme les « patatoïdes » de craie tracés par « Choquet » sur le tableau, autrefois.

Mais avant de l’effacer je la charge de sens ; ce sens vient après coup, je le sais. Je sais même que, d’année en année, sans sollicitations conscientes du souvenir, l’image s’est encombrée de nombreux sens successifs, confus, incohérents, contradictoires peut-être, et que celui que je lui donne aujourd’hui, pas si clair lui-même, n’est que leur résultante, compliquée et déformée de mon intention : commencer la « chromatographie » sur buvard de papier de ce mot ponctué, qui constitue à lui tout seul mon titre, Mathématique :. Cette image, ces images entrelacées les unes aux autres me sont revenues presque sans sollicitation dans l’air glacial de mai, sont entrées certes par hasard dans mon récit en résonance avec cet air froid de mai, en quelque affinité d’origine irrécupérable avec cet autre air froid semi-nocturne aussi, hivernal lui, de 1954, mais elles se sont présentées aussi en réponse à une décision narrative (→ § 15).

Il se trouve également que le mathématicien que j’ai été n’a plus, depuis quelques mois, qu’un rapport beaucoup plus léger, sans obligations, en partie ludique et sans grand sérieux (au sens des institutions proprement dites de la communauté mathématique) avec ce qui fut, à peine moins d’années que les trente-sept que j’ai comptées plus haut, une existence professionnelle. Je ne les enseigne plus, comme telles, selon un programme reconnu et sanctionné par une université (l’université de Paris-X Nanterre, en l’occurrence). Elles ne jouent qu’un rôle accessoire (même si inévitable) dans le « cours » ou « séminaire » de « Poétique formelle » dont je m’occupe à l’École des hautes études en sciences sociales (EHESS).

C’est pour cette raison vraisemblablement que j’ai cessé de me sentir coupable, non d’avoir renoncé à être, après le milieu des années soixante-dix, un mathématicien « pur » productif, ce que je n’ai jamais été que très peu, (et la « productivité » du mathématicien ne dépend pas seulement de sa volonté), mais plus impardonnablement d’avoir abandonné, pas totalement mais dans une large mesure, l’effort, ardu quoique nécessaire, de suivre le cheminement et la progression des idées dans les deux ou trois régions des mathématiques où j’avais réussi à comprendre, ou à croire comprendre, quelque chose de ce qui était en jeu. Le changement de statut qu’a représenté la reconnaissance institutionnelle partielle d’une activité de « mathématiques appliquées », dans une direction très spéciale, frivole aux yeux de beaucoup, la « poétique » !, qui s’était en fait substituée, dans les mêmes années, à des recherches proprement mathématiques, m’a libéré en quelque sorte de cette espèce d’obligation morale (et partant d’un remords) que je me sentais envers ce qui était une passion ancienne. Je me suis senti libre de ces attaches, et j’ai pu envisager d’entreprendre ce qui sera ce livre. Mais je n’ai pu le faire qu’en prenant acte d’un renoncement.

5 Ce qui provoquait la stupeur inquiète des étudiants de CDI

Ce qui provoquait la stupeur inquiète des étudiants de CDI de l’année universitaire 1954-1955 était l’irruption, sur la scène des savoirs reconnus et destinés à la transmission, de quelque chose d’étrange qui, sous le nom de « mathématiques modernes » allait, vague redoutable, déferler, en dépit de résistances farouches, sur la totalité du système éducatif.

Dans les années qui suivirent, le dessin, dont j’ai évoqué la présence sur le tableau de l’amphithéâtre Hermite, les deux ovales « patatoïdes » se coupant, leur partie commune pointée pour l’œil de l’assistance par des hachures obliques (caricature particulièrement agressive de ce qu’est une figure de géométrie ; plus élémentaire, et de loin plus « triviale », à contenu mathématique quasi nul, plus faible en tout cas que celui offert par les rectangles, carrés et diagonales que trace Socrate dans le Ménon (→ § 16)), allait surgir un peu partout en France, sur les cahiers d’écolier, sur les pupitres, sur le sable, sur la neige, sur les tableaux de toutes les classes, de tous les ordres et variétés d’enseignement.

Le voici, dans toute sa simplicité emblématique :

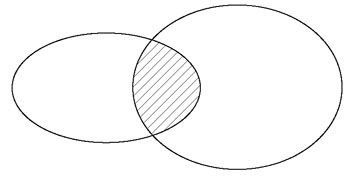
Fig. 1

Nous regardions, nous ne comprenions pas. Nous ne comprenions pas ce qu’il y avait à comprendre, en quoi cela faisait partie des mathématiques (habitués aux calculs algébriques, aux déri vées, aux intégrales, aux « coniques »). Au-dessous du dessin s’en inscrivait une « traduction » symbolique.

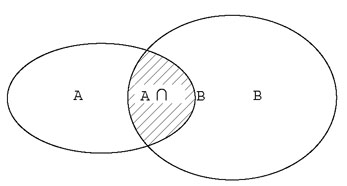
Fig. 1 (avec légende)

Les raisonnements qui s’ensuivaient, construits sur des figures à peine plus complexes que la première, à l’aide d’un tout petit nombre de symboles spéciaux, apparaissaient à la fois évidents (de très faible complexité déductive) et incompréhensibles dans leur finalité. La plupart des étudiants (comme plus tard des élèves, de la maternelle à l’université) se sentirent tomber sans parachute dans un territoire hostile.

C’est à quoi, cependant, il importait de s’habituer. Au bout de l’année universitaire, à quelques mois de distance à peine, il y avait des examens. Ces examens, il fallait les réussir. Il y eut des reçus et des collés. Je ne fus ni parmi les uns ni parmi les autres. On verra cela plus tard.

Je marque seulement maintenant l’importance sociologique du moment. Cette promotion d’étudiants fut la première à entrer dans l’enseignement des mathématiques en ayant bu à la source dite, pompeusement et abusivement, « théorie des ensembles » (la part « théorique », il faut bien le reconnaître, y était quasi nulle). Immergés brutalement dans le milieu lycéen, ils furent vite conscients de leur singularité, de leur originalité. On peut dire que, pour une bonne partie d’entre eux, il se produisit une véritable conversion (→ § 17) à une manière sentie nouvelle, audacieuse, inouïe, péremptoire, de voir les mathématiques. Aussi, tels les premiers disciples de Luther, ils furent les zélateurs réformés de la Mathématique moderne (variante : tels les adhérents à la Troisième Internationale après le congrès de Tours, ils furent les premiers bolcheviks d’une nouvelle doctrine révolutionnaire).

Je me trouvais là au début, parmi eux, moi aussi.

6 Le moment que je marque, symboliquement, au matin d’hiver,

Ce moment, le moment que je marque, symboliquement, au matin d’hiver, de l’évocation d’une place isolée dans l’amphithéâtre, l’associant de manière non moins symbolique et non moins arbitraire à la figure « ensembliste » sur le tableau, je me le représente aujourd’hui comme celui d’une difficulté et d’un désarroi extrêmes : sans doute le premier de ces quelques moments, peu nombreux, mais noirement mémorables, où m’est apparue, je dirai même : m’a sauté à la figure, l’extrême distance entre les hauteurs d’une intention, d’une ambition (ici intellectuelle ; en d’autres occasions artistique) et un état de fait qui se découvrait être presque exactement son envers.

Je n’ai pas été un mathématicien « naturel », de ceux qu’une vocation scolaire précoce, accompagnée d’une réussite brusquement spectaculaire et des encouragements de l’institution, conduisent, on dirait inévitablement, vers ce qui était alors en France le lieu de passage obligé, le réservoir de génies, la pépinière de talents, le centre d’entraînement d’athlètes de haut niveau dans cette spécialité olympique particulière, l’École normale supérieure, section des Sciences.

La comparaison avec les athlètes s’impose. Parmi les idées reçues sur les mathématiques (et comme beaucoup d’idées reçues, celle-ci comporte une large mesure d’imbécillité) il y a celle-ci : que le mathématicien se révèle très jeune, se prouve très jeune, ne demeure inventif, productif que quelques courtes années puis, telle la femme vue par le dix-neuvième siècle (comme le roman de Balzac, La Femme de trente ans, en témoigne dès son titre), perd rapidement son éclat et sa beauté mathématiques. C’est là, très exactement, le destin du coureur de cent mètres, discipline considérée comme la plus pure, la plus belle de l’athlétisme. Et l’athlète dont le don s’est évanoui avec l’âge n’a plus qu’un futur possible : devenir découvreur et entraîneur des nouvelles générations.

Dans cette conception assez universelle mais qui a été portée à son paroxysme en France, la mathématique étant le « sprint » des sciences, les meilleurs, ses vrais champions (à la fois au sens sportif et au sens médiéval), étaient les plus précoces, les plus rapides, ceux qui étaient partout, dès l’enfance, les premiers aux compositions trimestrielles, dans toutes les épreuves écrites et orales, s’assuraient les prix au Concours général, étaient admis dans les meilleures classes préparatoires, prenaient les premières places au concours d’entrée des Écoles normales supérieures, puis répondaient brillamment, non moins rapidement, à des questions laissées en suspens par les générations précédentes d’athlètes semblables à eux, démontraient des théorèmes à la douzaine, et enfin, exceptionnels parmi les exceptions, remportaient l’équivalent de la médaille olympique en découvrant mais surtout en démontrant le résultat spectaculaire auquel ils laisseraient leur nom.

Mon ambition n’a pas été celle-là. Et c’est heureux, car je n’y serais jamais parvenu. Je n’avais pas fait preuve des dons et des réussites nécessaires pendant ma scolarité. Je n’avais montré alors pour la discipline qu’un intérêt fort distant (les sciences étaient bien loin de mes préoccupations : je voulais être poète). Je ne l’avais pas choisie comme « voie » en entrant à l’université. Pourtant, un jour, j’ai voulu aussi être mathématicien. Mais alors, en quel sens ? Il y a là une difficulté de définition.

Elle ne m’était pas apparue tout de suite. Au début, un peu plus de deux ans avant le moment où je me suis placé au commencement de ce chapitre, plus précisément au mois de juin 1952, j’avais été comme saisi par une illumination. J’allais changer décisivement de voie. J’allais interrompre les études que j’avais entreprises, une licence d’anglais, presque terminée, le diplôme de russe de l’École des langues orientales, et m’orienter d’une manière radi calement différente ; repartir pour ainsi dire à zéro, recommencer.

Je n’allais pas, ce faisant, dévier de la voie qui m’importait le plus, la poésie ; mais cette voie-là, je venais d’en décider (ou de le découvrir), non seulement ne pouvait pas me fournir une orientation de vie susceptible de me nourrir ultérieurement (ce n’était pas une « profession » viable ; et ce ne devait pas, dans ma conception peu originale influencée indirectement par le surréalisme, être une profession du tout ; même si cela avait été possible, ce qui n’était pas le cas). Mais, plus sévèrement encore, j’en étais arrivé à la conclusion que toutes les études littéraires, pas seulement celle de la littérature française, étaient contradictoires avec la poésie comme activité d’invention : une « explication de texte » d’un sonnet des Chimères dans une classe de « première supérieure » du lycée Louis-le-Grand fut la cause (identifiée d’ailleurs a posteriori) de ce jugement.

Et je m’étais dit alors : je serai mathématicien ! (→ § 18.) C’était une idée ; seulement une idée ; mais ce fut une idée soudaine, une idée exaltante, bouleversante, illuminative (→ Bif. A). Je n’avais aucune espèce de compréhension réelle de ce que cela signifiait, des années ingrates d’un accomplissement laborieux, ni des qualités estimées indispensables pour accéder, dans cette direction, à une reconnaissance, à un statut. Je pensais que c’était une pure affaire de décision, comme pour la poésie. Je me disais : je serai mathématicien, de la même manière que je m’étais dit : je serai poète (je savais que je ne l’étais pas ; pas encore ; j’espérais le devenir) ; et je le serais, tout simplement parce que je le voulais.

C’était une idée sublime. Elle m’éclaira tout un été. De très loin.

7 J’ai souligné une analogie

J’ai souligné une analogie : je voulais être mathématicien, comme j’avais voulu être poète, en vertu d’une décision. Mais il ne s’agissait pas pour moi d’une décision du même type. Être poète, c’est composer de la poésie. C’est, avant tout, composer de la poésie. Être poète, c’est être avant tout poète, pas à côté d’autre chose, ni secondairement, ni provisoirement, pour un temps. Telles étaient, du moins, ma conviction et ma décision.

Je ne pouvais donc pas vouloir (encore moins décider de) être mathématicien comme je voulais être poète, selon les mêmes modalités. Je ne voulais donc pas, au moment de ma décision, composer, inventer des mathématiques.

(À vrai dire, je ne savais pas ce que cela pouvait bien signifier. L’institution scolaire, pendant mes années d’études, ne donnait aucune idée, absolument aucune idée de la mathématique comme discipline en mouvement. Elle apparaissait arrêtée : il y avait cela, (telle construction, tel objet, tel calcul) qui se faisait comme cela, qui s’était apparemment toujours fait comme cela, depuis les Grecs, ou presque. Résoudre un problème mathématique, c’était aller d’un point, l’énoncé, à un autre, la conclusion, préalablement donnés tous les deux, et toujours dans le même sens : il n’y avait à découvrir (et à découvrir vite) que le chemin pour y parvenir. Je caricature à peine.) (→ § 20)

Or j’avais décidé que je voulais, et voulais seulement comprendre. Non pas comprendre ceci ou cela, tel passage de telle hypothèse à telle conclusion, telle meilleure manière de conduire un calcul, mais comprendre, sans complément. D’une lecture, plus ou moins paresseuse, de Descartes, du Timée (l’un des dialogues platoniciens de la bibliothèque de mon père), de quelques autres bribes philosophiques, d’un vague examen des attendus de la classification des sciences (telle qu’on l’enseignait en classe de « philosophie » des lycées), je m’étais persuadé de la nécessité des mathématiques pour la compréhension du monde. J’aurais été bien en peine d’expliquer ce que cela voulait dire, sinon que c’était une chose souhaitable, un but que l’on pouvait se fixer, une ambition intellectuellement et moralement estimable. Anachroniquement (par rapport à moi-même) et un peu pompeusement je pourrais l’articuler ainsi : Dieu, nous a dit Galilée, a écrit le monde en langue mathématique. Pour comprendre le monde, le déchiffrer, il faut connaître cette langue. Bon.

J’en espérais aussi, sans le formuler très explicitement, des bénéfices indirects pour l’exercice même de la poésie. Autant j’avais senti l’examen critique, la lecture scolaire du poème comme un poison mortel pour la pratique de la poésie, idée que la découverte des surréalistes avait très tôt implantée en mon esprit, autant la discipline, la rigueur, la sévérité du calcul (« ô mathématiques sévères ! ») semblaient pouvoir servir d’isolant intellectuel, et même de protection (→ § 22). Persuadé de l’hétérogénéité absolue de ces deux activités, je pensais avoir tout à gagner de l’une, la mathématique, pour défendre l’autonomie irréductible de l’autre, la poésie.

Il y avait une autre différence, dont j’étais certes conscient, mais qui au début, au temps de la pure imagination estivale de ma nouvelle voie, me parut être un avantage, un profit supplémentaire à retirer de ma décision : si je choisissais de nouvelles études, des études de mathématiques, je devrais le faire de manière à les poursuivre jusqu’à un terme professionnel, qui pouvait peut-être même n’être pas l’enseignement. La poésie était une affaire strictement personnelle, mais les mathématiques étaient un objet reconnu socialement. Je pourrais non seulement vivre avec, mais vivre par elles (au sens où on emploie l’idée de vivre dans l’expression « gagner sa vie »).

Or, si l’abord scolaire de la poésie et même du roman me repoussait (non pas d’ailleurs en soi, idée reçue mais bête, mais en me plaçant du point de vue de celui qui ne veut pas que lire et étudier), plus difficile encore était d’envisager (et les études littéraires n’offraient guère d’autre perspective) de devoir m’y livrer moi-même, comme enseignant (la profession la mieux connue de moi, parce que celle de mes parents, et la seule où on pouvait espérer disposer de temps à soi). Les mathématiques se présentèrent alors comme une évasion. Les enseigner, quand j’en viendrais là, serait une activité neutre par rapport à la poésie.

Telle était la vision à la fois exaltante et raisonnable qui m’avait guidé. À l’automne de 1952 je repris le chemin d’un lycée, qui fut le lycée Jacques-Decour à Paris, au pied de la butte Montmartre, (anciennement ce collège Rollin où enseigna Stéphane Mallarmé), et je pénétrai dans la classe de mathématiques supérieures d’un ancien condisciple de mon père, un ancien normalien comme lui, de la même promotion, Mr Durrix, dit « le Dur », qui avait bien voulu accueillir le « littéraire » sans références que j’étais. C’était, comme on disait, une « petite hypotaupe », qui ne cherchait pas à rivaliser avec les grandes, Saint-Louis, Louis-le-Grand ou Henri-IV, et où le « climat » n’était pas trop rude.

Au début, ça allait.

8 Mais pas longtemps.

Mais pas longtemps. Je me débrouillai assez convenablement pendant la première année : mon « illumination » de l’été était encore proche, la nouveauté de la situation n’avait pas encore perdu de son charme, ni la rigueur scolaire de son éclat.

Mais quand je dis « convenablement » je veux dire en mathématiques. Car je découvris avec une irritation certaine qu’on n’étudiait pas que cela. Je m’en doutais bien un peu, puisque ces classes préparaient à Polytechnique et autres écoles d’ingénieurs, mais je n’avais pas prêté suffisamment attention aux implications redoutables de ce fait.

Or j’eus immédiatement des difficultés avec la physique. Non seulement ma maladresse manuelle était grande, mais une maladresse plus grave, de nature intellectuelle, me paralysa rapidement. Je n’avais pas, a priori, de prévention contre la physique (je ne parle ici que de la discipline scolaire, dans l’état où elle se trouvait enseignée vers 1950) ; simplement le sentiment parfaitement non réfléchi de son caractère « secondaire » et « dérivatif » par rapport aux choses sérieuses (l’Algèbre, l’Analyse). Je ne m’attendais donc pas à y rencontrer de difficultés particulières ; un peu d’ennui, peut-être, envers lequel il faudrait se montrer patient, et magnanime.

Ce qui se produisit fut alarmant et inattendu. Certes, tout ce qui était calcul semblait assez simple, une fois les données physiques traduites en symboles reconnaissables par un être doué de raison calculatoire (→ § 22). Mais je ne savais pratiquement jamais effectuer convenablement cette traduction. J’ai dit précédemment que ce qui était demandé à l’élève était d’aller d’un point initial, les données d’un problème, à un point final, la conclusion à démontrer. J’aurais volontiers effectué ce parcours, mais, dans les problèmes de physique scolaire, d’électricité ou d’optique qui m’étaient proposés, j’avais l’impression exaspérante que des renseignements implicites, évidents pour tout le monde (sauf pour moi !), m’étaient dissimulés, et il m’arrivait souvent de rester un temps indéfinissable devant l’énoncé, sans savoir par quel bout le prendre. Je me décourageai rapidement.

Pourquoi, dans ces conditions, avais-je choisi de persévérer aussi longtemps dans cette direction ? Après tout, à l’université, pendant l’année initiale, le certificat de Mathématiques générales, il n’y avait pas de physique au programme. (La physique, et la mécanique, autre horreur, attendaient le mathématicien au tournant, mais plus tard, pendant sa licence.) C’est que la discipline sobre et la régularité des « prépas » m’avaient paru indispensables pour quelqu’un qui, comme moi, ne savait rien, ou plus rien de ce qu’il avait appris au lycée.

À mesure que l’année scolaire avançait, j’étais en proie à l’insatisfaction. Et elle ne venait pas seulement de mes difficultés imprévues avec la physique, à peine compensées par l’amusement de la chimie, ou de la catastrophe de ma rencontre avec la géométrie descriptive, que mon incapacité à dessiner rendait férocement rébarbative. Sa cause était à la fois plus indirecte et plus grave, plus générale aussi. Je ne comprenais pas.

Je ne comprenais pas ce que j’étais venu essayer de comprendre, à savoir :

a) ce qu’étaient les mathématiques (en un sens à la fois absolu et flou du prédicat d’existence) ;

b) comment elles servaient à la compréhension du monde.

Je questionnais parfois « le Dur », après la classe (plutôt indirectement, la question telle que je me la posais était de nature privée). Je cherchais à savoir de lui ce qu’il y avait après, après le programme de « sup », après celui de « spé » (les « mathématiques spéciales » de la seconde année). Mais il ne me répondait que vaguement.

Il m’apparaissait que la suite comportait une large dose de « même » : du calcul intégral plus compliqué, des équations différentielles plus difficiles, etc., etc., qui servaient certes d’outils indispensables aux mises en forme les plus ambitieuses de la physique, de la cosmologie comme de la fabrication des ponts. Mais si c’était là tout ce qu’on pouvait en attendre, je ne risquais pas d’obtenir un jour la réponse à mes interrogations. Je ne voyais pas cela aussi précisément que je le dis maintenant, mais l’insatisfaction était là.

Ma deuxième année fut un désastre. L’impulsion initiale, produit de mon illumination, s’était épuisée. Je cessai de m’imposer le labeur nécessaire, qui me parut en fait peu différent dans son essence de celui des versions ou thèmes anglais, des dissertations sur Shakespeare ou Milton. Médiocrement reçu en « math-géné » (certificat de Mathématiques générales), je m’inscrivis en licence (et aussi à un dernier certificat d’anglais en vue de l’autre licence, « Civilisation américaine » ; après tout, peut-être faudrait-il que je renonce, que je reconnaisse mon erreur, et revienne en arrière). Je pénétrai avec la foule compacte des étudiants de CDI dans l’amphithéâtre Hermite, y choisis une place peu visible, et, comme beaucoup d’autres, en écoutant les premiers cours, je ne compris rien.

9 Le temps de ce mois de mai change peu à peu,

Le temps de ce mois de mai change peu à peu, devient de moins en moins semblable à mon souvenir hivernal.. Les premières heures des jours restent froides, le ciel presque engourdi d’un air froid, liquoreux-glacial, couleur de glace, sa lueur pénétrante venant jusqu’à moi sans cesse plus tôt, malgré l’heure d’été, par ma fenêtre pourtant voilée, s’insinuant sous mes défenses : la lampe, l’écran allumé devant moi, le silence de la cour vide, de la ville abandonnée, plate, immobile.

Très vite, avec le soleil, il fait chaud : une chaleur d’été, déplaisante, sans légèreté. Mais pendant les premières heures de la matinée, deux modes d’existence de l’air coïncident, de part et d’autre des frontières de l’ombre : sous les arbres, sur les bancs de pierre nue et lisse du jardin des Tuileries, à quelques centimètres du gravier mêlé de sable balayé de chaleur, l’air reste net, froid. Il le reste jusque vers dix, onze heures, avant de fondre au soleil, comme une glace d’entracte, un « Esquimau » dans les cinémas de jadis, sur les doigts.

Le jardin des Tuileries est en « réfection ». Dans l’« allée des Feuillants » on lit :

Travaux de revitalisation des arbres

pour décompactage profond et superficiel

et apport d’engrais.

Un accès de transparence des autorités jardinières les a poussées à informer les « lecteurs » de ce jardin, ceux qui, comme moi ce matin, viennent paresser dans ses pages de marronniers, d’allées ombreuses, ponctuées de bancs, qu’elles se livrent, sur quelques mètres, le long du fossé, à des essais de « sables triturés » (mêlés de graviers concassés), essais destinés à éprouver divers mélanges en vue du choix définitif (choix qui sera effectué selon des critères d’élasticité, de résistance et, sans aucun doute, de coût) de celui qui sera offert aux semelles des piétons et aux pattes des chiens.

Il n’est pas prévu d’associer le public à ce choix, où les critères de couleur, de finesse, de grain, de provenance même ne joueront, je le crains, aucun rôle. Des panneaux, que je n’ai encore vu personne lire, précisent, indications en clair accompagnées de chiffres peu interprétables et peu remarqués, comme ceux qu’on peut lire partout dans les rues, au pied des immeubles, sur les plaques d’égout, destinés aux professionnels du soin des rues, aux pompiers, aux entreprises de terrassement, aux dératiseurs, que sais-je… :

essai n° 9

Sable blanc quartzite

essai n° 6

Sable roulé de l’Oise

essai n° 5

Sable ciment couleur blanchâtre grave laitier

essai n° 3

0/6 de Seine 0/4 concassé.

J’admire.

Le soleil, aidé d’un peu de vent, agite des étincellements de petites vagues à la surface du bassin. Les canards y circulent très près du bord. Je suppose que d’une part ils sont ainsi mieux à même de recueillir les offrandes comestibles des visiteurs, d’autre part qu’ils ne tiennent pas à se trouver à portée des carpes qui font des sauts véritablement dolphinesques et ont une sale gueule. Comme je les comprends.

Tout immergé dans la fraîcheur, face au ruissellement d’étincelles du bassin, (→ § 24) je me livre à une rumination prospective ; dire que je réfléchis serait excessif, l’environnement ne s’y prête pas. J’ai éteint mon écran de Macintosh LC, quitté ma chambre, marché sans me presser jusqu’ici par la rue de Clichy, la Trinité, l’Opéra, la place Vendôme, et je me demande comment poursuivre, quel chemin choisir pour avancer demain dans cette agitation du souvenir, cette remémoration, cette description, cette explication, cette élucidation.

Ce qui n’est plus à ma portée, en tout cas, c’est un renouvellement, un nouveau départ, un recommencement absolu. Ce que j’essaye de comprendre, ce que je tourne et retourne réflexivement n’est pas de l’inconnu, du neuf, du jamais-vu. Je ne m’efforce ni de découvrir, ni d’inventer, ni de démontrer. Je fouille dans le révolu, l’irréversible ; dans l’oubli.

Je pense à ce proème de Dante, aux lignes infiniment séductrices de son début :

« In quella parte del libro della mia memoria, dinanzi a la quale poco si potrebbe leggere, si trova una rubrica, la qual dice : INCIPIT VITA NOVA. »

J’avais trouvé ce mot : Mathématique. Il m’avait offert, croyais-je, une vie nouvelle. Grâce à lui, grâce à elle, une vita nova allait commencer, s’ouvrir pour moi. J’avais, ensuite, conclu à une illusion.

Je regardais, enfoncé contre le mur de l’amphithéâtre, non vers le tableau, mais vers l’extérieur nocturne envahi d’une autre illusion, celle de l’image virtuelle de la lumière, des visages, trouble, vaporeuse, suspendue en l’air glacé. Comment être ailleurs ? et où ? Et pourtant, c’était vraiment une vie nouvelle qui allait m’être donnée. Bien entendu, comme toujours, j’allais l’ignorer, et ne la reconnaître qu’au moment où je saurais qu’elle avait été ; et n’était plus.

Incises du chapitre 1

10 (§ 1) échapper à la vigilance de l’administrateur de l’institut

Il s’appelait Paul (?) Belgodère. C’est-à-dire qu’il s’appelait pour nous, ses « ouailles », « Belgodère ». « Belgodère » était devenu aisément « belgodère », sans majuscules, c’est-à-dire moins la désignation d’un individu porteur d’un nom propre que le nom commun d’un symbole administratif ; c’est-à-dire encore, pour ses adversaires individualistes ou politiques (généralement communistes), l’obstacle principal à l’expression de leur imprescriptible liberté (pour les uns) ou (pour les autres) le symbole de la fausse neutralité, dite « formelle », étatique, indépendante en surface, en fait profondément et secrètement au service de la bourgeoisie.

Il assumait avec zèle et enthousiasme ces deux rôles. Ses réactions n’étaient pas à vrai dire proprement politiques. Il était avant tout l’incarnation du bâtiment dont il avait la charge. Il se sentait responsable des horaires des cours, du chauffage, des ampoules électriques, de la propreté des toilettes. « Je suis le seul agrégé de mathématiques, nous dit-il un jour fièrement, dans un accès de confidences (nous étions déjà de vieux et familiers adversaires) à balayer dans les chiottes. » Nous ne lui opposâmes pas l’exemple de ceux qui se livraient à des tâches semblables dans les armées de la République (alors mondialement fameuses pour leur utilisation des compétences), puisqu’il ne s’agissait pas de volontaires.

Or il avait affaire à forte partie. Car la génération « bourbakiste » fut, aussi, une génération turbulente ; d’une turbulence, je dirai, arithmétiquement conditionnée : l’IHP débordait de partout. Et « belgodère », selon sa « PSA » (« philosophie spontanée de l’administrateur »), aurait voulu des étudiants quasi immatériels, incolores, inodores et sans saveur ; bref, qu’ils ne soient, comme les enfants selon la conception victorienne, « neither seen nor heard » dans les lieux.

Il n’était donc pas plus un nom propre que « choquet » mais, n’étant pas protégé par la fonction professorale, il n’échappa ni à notre hostilité ni à nos insolences. Il passait une énorme partie de son temps à guetter nos transgressions, y répondant par des brimades, nous expulsant et fermant à clef des salles inemployées, nous interdisant ainsi l’usage des tableaux noirs et craies tranquilles qu’elles nous offraient, loin du brouhaha surpeuplé de l’unique « Salle des étudiants », totalement inadaptée à nos effectifs, veillant tel le chien des Enfers antiques à la porte de la Bibliothèque pour en réserver l’entrée aux professeurs et chercheurs. Cette situation n’a rien d’exceptionnel : simple préfiguration de ce qui bientôt allait être le sort commun dans la quasi-totalité des établissements universitaires (et durait encore, quand je l’ai quittée en 1991, dans l’université de Paris-X Nanterre), avec cette simple différence qu’après 1968 il n’y eut plus nulle part de « belgodère » pour s’efforcer d’y maintenir un semblant d’ordre.

Au moment le plus chaud de la lutte certains lancèrent même, s’inspirant d’événements contemporains, le mot d’ordre caractéristique de « débelgodérisation de l’IHP ».

Ce furent certainement pour lui de dures années. Pourtant, le départ subit des hordes de barbares pour les pâturages plus verts de « jussieu » ne sembla pas lui apporter la sérénité. Car si les couloirs et les amphis redevinrent propres, il n’y eut plus guère d’occasion de les défendre contre les envahissements et les débris. Avec le temps, dans les dernières années de sa vie (il ne quitta jamais l’institut), sans doute mais pas uniquement parce que nous étions devenus des enseignants respectables, la vieille hostilité, qui avait été de sa part toujours « générique », impersonnelle, avait fait place à une sorte de reconnaissance bourrue pour ceux qui continuaient à venir dans ces lieux sacrés. Bien volontiers il nous ouvrait les salles, vérifiait la propreté des tableaux, la présence de craie et de chiffons. Mais on sentait qu’il était bien proche de nous dire : « dans l’IHP désert quel devint mon ennui ».

11 (§ 2) Du passé (mathématique) on avait fait, apparemment, table rase

Pour beaucoup, et d’une manière plus ou moins réfléchie, le « bourbakisme » semblait (largement à tort, bien entendu, mais pour ne pas être tenté par cette interprétation il aurait fallu être plus savant (et d’ailleurs certaines « exagérations » des maîtres, comme le célèbre cri de Jean Dieudonné sautant sur place de toute sa hauteur lourde (disait la légende peut-être apocryphe), tel un lanceur de marteau aux jeux Olympiques, sur l’estrade d’un congrès de l’APM, l’Association des professeurs de mathématiques, et lançant un tonitruant « À bas Euclide ! », rendaient ce glissement fort vraisemblable)), semblait, dis-je, ruiner l’édifice de toutes les mathématiques antérieures et rebâtir un édifice entièrement neuf. « Le monde à bas, je le bâtis plus beau ! »

Et, bien sûr, on ne pouvait alors qu’être frappé d’une analogie avec une autre « théorie de la table rase », celle des révolutionnaires, telle qu’elle s’exprime dans un couplet de l’Internationale : « Du passé faisons table rase/ … le monde va changer de base. » Sur la table rase des anciennes manières de calculer et de déduire, le monde mathématique, tel le (et en préfiguration du) monde « réel », allait recommencer. C’était une perspective exaltante, et surtout bien moins lointaine que l’autre, la politique.

Il apparaissait aussi, dans cette interprétation – et le désarroi des « anciens » de l’amphi ou les visages perplexes, les réticences, les sarcasmes même de certains mathématiciens des générations antérieures le confirmaient abondamment –, que faire le choix « révolutionnaire » en mathématique mettait d’emblée sur une sorte de « voie royale » (celle dont un successeur des pharaons s’était entendu avertir autrefois, dit-on, qu’elle n’existe pas en ce domaine). On irait plus loin et plus vite, on atteindrait plus aisément les grands secrets, on en découvrirait peut-être, dans quelque région non encore illuminée du paradis ensembliste, ce paradis créé pour nous mathématiciens, selon le mot de Hilbert, par Cantor, dont « nul ne nous délogerait » jamais, et dont l’archange Bourbaki dessinait avec rigueur les cartes. « Nous ne sommes rien, soyons tout ! »

En ce qui me concerne, un autre parallélisme encore s’imposait, fallacieux également, mais je n’allais le découvrir que beaucoup plus tard. Et celui-là était en fait parfaitement explicite : la révolution (politique), l’esprit révolutionnaire avaient eu leurs analogues aussi dans la poésie : c’est ce qu’avait énoncé explicitement le mouvement surréaliste.

En poésie aussi, le monde ancien avait été mis à bas. La liberté avait triomphé. L’illumination moderniste avait, à la suite des révolutionnaires de la fin du siècle passé, mis fin aux formes dépassées et réactionnaires de la tradition vieillie. C’est une idée qu’on trouve encore, sous une forme burlesque, dans la théorie, bien oubliée depuis, due à Julia Kristeva, de la « Révolution du LP (le langage poétique) ». D’où la « moyenne proportionnelle » évidente : le vers libre est à l’axiomatique ensembliste ce que la géométrie euclidienne est à l’alexandrin.

(Je ne cacherai pas qu’une contradiction évidente apparaissait alors dans cette belle perspective triangulaire : révolution-mathématique-poésie. Car Aragon, dont l’autorité politico-poétique était grande dans mon entourage, préconisait au même moment le retour au vers traditionnel (s’étant remis lui-même, dès 1939, à pratiquer particulièrement le dodécaphone). Il ordonnait l’emploi des seules mesures « vraiment rythmé(es), vraiment compté(es) » (comme écrivait Eluard vers la fin de sa vie), pratiquant, lui, la méthode Coué. Il s’agissait d’un alexandrin post-rimbaldien et post-apollinarien, certes, mais quand même ! Je ne savais comment me dépêtrer de ces difficultés « théoriques », sans renoncer à une exigence exacerbée de cohérence.)

12 (§ 3) « alpha point alpha point alpha alpha point point point »

Cette expression n’est que la forme incompréhensible (pour cause de non-familiarité) d’un objet en fait assez simple. Il s’agit de la représentation d’une abstraction, une abstraction nommée « arbre ». L’objet formel « arbre » n’a en fait pas de tronc, seulement des nœuds de branches (notés par des points) et des branches (qui sont des segments de droites), se terminant par d’autres points (des nœuds de branches possibles mais sans branches, vides de branches) ; ce sont les « feuilles ». L’expression citée est un arbre en ce sens, dont la figuration « géométrique » serait :

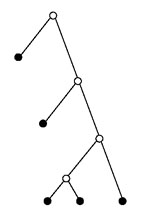
Fig. 2

On remarquera que la convention, partagée par les linguistes, les informaticiens et les quelques mathématiciens qui s’y intéressent, amène à dessiner les arbres comme orientés vers le bas, racine en l’air, à l’envers en somme. Étrange !

Considérant les « points » de la notation comme des objets singuliers pleins, indécomposables, dont il n’y a rien d’autre à savoir que leur singularité isolable, qui les rend indiscernables, on peut interpréter l’arbre, « algébriquement », comme une superposition de groupements, le symbole du groupement étant désigné par « alpha ». « Alpha point point » signifie le groupement composé de deux « points », et c’est un arbre particulièrement simple, à deux branches, deux feuilles (nommées « points ») et un nœud, nommé « alpha ».

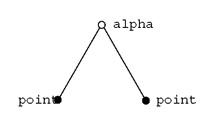
Fig. 3

On peut ensuite grouper les groupements eux-mêmes, les superposer, en conservant toujours la condition d’un unique mode de groupement, par deux toujours, toujours du même « nom ». Cela revient à prendre les feuilles de l’arbre élémentaire ci-dessus comme les nœuds d’un nouvel arbre :

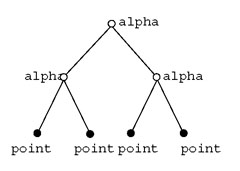
Fig. 4

L’espèce d’arbres ainsi construite, dont l’arbre étudié fait partie, est celle des arbres « binaires ». Dans l’interprétation en « groupements » on parle de « parenthésages » ; ce sont des « parenthésages binaires ». (On pourrait mettre les points ou les groupements déjà parenthésés eux-mêmes entre de nouvelles parenthèses. L’assemblage de symboles :

« alpha point alpha point alpha alpha point point point »

se traduirait, écrit parenthétiquement, ainsi :

(. (. ((..).)))

L’écriture choisie, dite « écriture polonaise », est plus « économique » en symboles (et en dimensions : elle n’est pas « planaire » comme la représentation géométrique, mais linéaire, comme l’écriture ordinaire). On n’écrit que les « parenthèses ouvrantes ». La place de leur fermeture est alors uniquement déterminée. On peut envisager des parenthésages (et arbres) ternaires, n-aires même, avec plusieurs sortes de points, plusieurs sortes de manières de grouper, plusieurs noms d’embranchements…

Si on interprète alors la géométrie des arborescences, en la projetant sur la feuille, comme une cartographie, l’écriture en alphas et points apparaît donc comme une écriture strictement linéaire, strictement orientée, une traduction sans retours, sans mémoire, d’une figure en arbres. Elle entretient donc un rapport analogique avec la manière de noter linéairement que j’emploie dans ce livre, qui soumet aux exigences de l’objet imprimé et de sa lecture la cartographie en partie arborescente du récit. (Une différence étant que la géométrie des arbres n’admet aucun de ces retours que s’autorise la prose : aucune branche de l’arbre ne revient à son point de départ, pour s’autogreffer ; il n’y a pas de « boucle ».)

13 (§ 3) une autre porte, tout en bas, à gauche cette fois du tableau

Un samedi matin de ce même mois j’ai eu soudain envie de revoir les lieux que j’étais en train d’évoquer dans ce chapitre. J’ai descendu la rue d’Amsterdam jusqu’à Saint-Lazare, pris un autobus 27 à deux wagons (pas, hélas, à deux étages), montant à l’arrière m’asseoir sur une des deux banquettes à trois places qui se font face à l’avant de ce wagon-là (la plus proche de la porte, et à la place qui est, des trois, également la plus proche de la porte), et je suis descendu, dans la rue Gay-Lussac, à l’arrêt le plus favorable, devant l’Institut hispanique, de l’autre côté de la rue dans ce sens-là.

Mais j’étais venu jusque-là en vain (c’est pourquoi je me venge de cette déconvenue en l’introduisant dans cette incise). L’accès à l’IHP était impossible : toutes les grilles étaient fermées.

J’ai fait le tour lentement, par la rue Pierre-et-Marie-Curie, la rue d’Ulm (examinant au passage l’état actuel de l’ancien café « Plantin » (fort prospère)). La voie d’accès automobile était ouverte pour cause de travaux, et j’aurais pu entrer par là, mais à quoi bon, puisque l’IHP lui-même était sans aucun doute fermé aussi.

J’insisterai sur le fait que je n’ai pas fait cette tentative de retour sur les « lieux du crime » avant de les avoir décrits (je dis « retour sur les lieux du crime » pour tous semblables pèlerinages parce qu’ils s’accompagnent presque toujours d’un vague sentiment de culpabilité ; comme si je m’attendais toujours à y être contredit par le présent, et qu’en même temps je me sentais responsable des contradictions survenues dans mes souvenirs).

Je me soumets, aussi scrupuleusement que possible, à l’engagement de véridicité que j’ai pris dès le commencement de mon entreprise (et respecté dans les deux volumes (branches) déjà publié(e)s). La vérité du souvenir n’est pas la vérité de la conformité du souvenir avec les choses souvenues.

Je suis revenu en semaine. Tout était ouvert, mais vide : une absence fantomatique d’activités. Je suis quand même allé jusqu’au bout du couloir central (les salles de cours à gauche ont disparu, remplacées par des bureaux). J’ai ouvert la porte de l’amphi. Les commandes des mouvements du tableau était placées en bas à droite (mais peut-être est-ce là une modification relativement récente). Le reste sans surprise.

14 (§ 4 ) un livre est l’autobiographie de son titre

Si un livre est autobiographie de son titre, qu’en est-il spécifiquement de celui-ci, ‘Mathématique :’, qui couvre, avec une évidente désinvolture, bien autre chose que ce qu’il semblerait annoncer ? Admettons l’analogie, proposée par cet aphorisme dérivé de Stein, entre le déploiement, le déroulement du livre à partir de son nom, le titre et le récit autobiographique. Si je lis sur une couverture David Copperfield, je m’attends, il est vrai, à ce que le roman me raconte la vie de David Copperfield ; et, comme le livre est identifiable ainsi, par ce nom, et n’a pas d’autre existence matérielle, c’est bien de la vie de ce « David Copperfield », dont le nom fait le titre du livre, que le livre parle. Admettons encore que, métaphoriquement, à la mathématique puisse être donnée un statut semblable (il y a deux différences, que je néglige : dans le roman de Dickens, le nom de David Copperfield n’est pas suivi de « deux points » – il n’est pas pris entre deux ‘ ’), il reste à se demander : de quelle vie de la mathématique s’agit-il ?

Il ne s’agira pas, principalement, de la vie de la mathématique dans la mienne. Il ne s’agira pas, principalement, d’une sous-histoire de mon histoire, de cette partie de l’histoire (au sens large) qui englobe ma découverte d’une certaine idée de la mathématique, ni de l’influence que cette découverte a eue sur les circonstances de ma vie. Mais seulement de ce qui, dans ces circonstances, mérite mention, sous la visée d’une entreprise que je note Projet. Il s’agit de ce Projet, principalement.

Le livre qu’est cette branche trois du ‘grand incendie de Londres’ fait partie de ce que ‘Le grand incendie de Londres’ est, en partie (en partie seulement d’ailleurs, car il n’est pas que cela ; et n’est certainement pas principalement cela, en tout cas pas directement), de ce qu’il est conformément à son titre, c’est-à-dire une biographie de ce que je désigne par Projet (ou autobiographie, si on veut, mais seulement au sens banal où il s’agit de mon projet, regardé et raconté par moi).

Il y a donc un emboîtement, un plongement, un embedding : La mathématique apparaît, pénètre, prédomine, puis recule dans ma vie, mais principalement en tant qu’elle joue (pénètre, prédomine provisoirement, puis recule) dans la conception et articulation du Projet. Et le récit de cet emboîtement commande et justifie, si tant est que quoi que ce soit de ceci soit justifiable, l’emboîtement d’une branche intitulée ‘Mathématique :’ parmi les x branches programmatiques d’un récit, ayant à voir avec le Projet (et partiellement ayant à voir avec lui de manière « biographique »). Elle en raconte les prémices (et prémisses).

Ce qui implique deux choses : la première, que le titre de cette branche n’est pas Mathématique mais ‘Mathématique :’, c’est-à-dire en situation de dépendance et de « boitement » (substantif hybride des actions de boiter et d’emboîter) par rapport au titre qui n’est pas le sien ; la dépendance étant exprimée, signifiée de manière citationnelle, et le « boitement » évoqué par l’adjonction du signe de ponctuation ! ;

la deuxième, que ce rapport de dépendance et de boitement renvoie de façon évidente au rapport de dépendance et de boitement qui existe entre ‘Le grand incendie de Londres’ (titre général de ce que j’écris) et Le Grand Incendie de Londres, le roman que je n’ai pas écrit, né et mort avec le Projet. (→ branches un et deux ; branche un surtout) (Ajouté en 1995 : Je signalerai enfin que, pour des raisons indépendantes de ma volonté (un blocage insurmontable de plus d’une année), le présent volume ne représente que la première partie de cette troisième branche.)

15 (§ 4) ces images entrelacées se sont présentées en réponse à une décision narrative.

Toute décision narrative, tout commencement de raconter met nécessairement en mouvement la mémoire : en un mouvement désordonné, une prolifération imprécise, une débauche, pas même d’images, mais de bribes et ébauches d’images. Il s’y produit, quasi instantanément, quelque chose comme une explosion de temps. (Dans le magma de débuts d’images surgies à l’instant du mouvement de souvenirs que je viens de susciter pour m’avancer dans cette incise, je découpe une métaphore : « explosion de temps ». Elle tente de saisir, en un condensé de langue, un principe de transition. Une violence de souvenirs offre du temps, du temps chaotique, mais passé. Il m’était apparu, pour représenter cela (il vient juste de m’apparaître) un vers : « Les explosions du temps, fruits toujours mûrs pour la mémoire/ »).

Chaque tentative volontaire de susciter le passé, si elle ne se heurte pas à une grisaille molle, affronte de telles « explosions ». Le prélève ment d’images, le dépôt de phrases qui assurent la visibilité narrative des visions associées au présent intérieur ne font pas que les maîtriser, comprimer, contrôler, ralentir. Les arrêts sur images, les phrases s’efforcent d’apprivoiser l’enchevêtrement hirsute des souvenirs, de le rendre manipulable pour le récit, de le convertir en entrelacement de pictions stables et définies. J’invente un jeu de mémoire (ici un jeu délibéré).

Dans cette branche comme dans les deux précédentes, je m’efforce de rester absolument fidèle à ce donné des souvenirs ; un donné qui ne peut être, lui, que très partiellement fidèle aux souvenirs eux-mêmes : la moindre attention aux processus d’observation du phénomène de remémoration me montre que l’appareil d’investigation que je suis forcé d’utiliser, le regard conscient, son insistance, sa fixité et sa lenteur, aidé de l’outil de la langue, est encore moins séparable de son objet que le fait physique « quantique » des dispositifs matériels, des protocoles de sa mesure comme de la logique interne de sa définition. (Je ne suppose pas pour autant la moindre influence physique que ce soit de mon regard observateur sur le système observé des souvenirs. Le langage est l’appareil d’observation de la mémoire. À travers lui je me définis comme son observateur local.)

Mais la stratégie de fonctionnement du jeu de mémoire s’oppose délibérément à celle que j’ai utilisée dans la branche deux, dont le titre est La Boucle. J’avais alors mis en scène de prose une séquence d’images-mémoire, des jeux locaux de mémoire contraints seulement par des bornes chronologiques, qui constituaient un point de départ antérieur à la construction narrative, qui se contentait, elle, de les suivre, plus ou moins séquentiellement.

La démarche, dans la branche présente, est inverse. Je vais chercher volontairement les images-mémoire adéquates au sujet, et des faisceaux de telles images fortement corrélées (dans leur sémantique comme dans leur chronologie), pour les faire servir à l’avancée dans la voie d’un déploiement : celui du ‘grand incendie de Londres’ dans son ensemble, qui doit satisfaire à une définition, décidée bien que laissée implicite, et satisfaire aussi, branche après branche, à un aspect particulier de cette définition.

Il s’ensuit que j’émonde volontiers les végétations excessives au regard de mon intention qui poussent dans les arborescences d’images quand elles répondent à mon appel. Je ne les modifie pas, ce serait contraire à l’éthique auto-imposée de mon livre, je les simplifie. Je les colore d’un sens sinon consciemment anachronique, du moins prêt à ce risque, introduit en elles au futur antérieur, à partir du futur de la narration, où elles en rencontreront d’autres, pour ce que je nomme un entrelacement.

16 (§ 5) les rectangles, carrés et diagonales que trace Socrate dans le Ménon

(Entrent monsieur Ménon, Socrate et le Petit.)

Monsieur Ménon (M.). – Toi, viens ici.

Socrate (S.). – Ôte-moi d’un doute. Connaît-il bien le grec ?

M. – Oui, bien sûr, il est né dans ma maison.

Le Petit (P.). – Efkharisto poli. Touristiki to phageton.

S. – Fais bien attention. Vois s’il anamnèse ou s’il apprend de moi.

M. – Je ferai attention.

S. – Dis-moi, petit, sais-tu que ceci est un espace à quatre côtés ?

P. – Je le sais.

S. – Sais-tu qu’en cet espace ces côtés, qui sont quatre, sont égaux ? Sais-tu que leurs longueurs ont la même vertu, sont de même mesure et compte, le sais-tu ?

P. – Peut-être.

S. – Et que ces lignes qui passent par le milieu sont aussi égales ?

P. – Oui, Socrate.

S. – Un tel espace ne pourrait-il pas être plus grand, ou plus petit ? Parle sans t’émouvoir.

P. – Je suis jeune, il est vrai, mais aux âmes bien nées, la valeur n’attend pas le nombre des années. Je réponds : Oui.

S. – Si ce côté a deux pieds de long et ce côté-là aussi, combien de pieds aura le tout ?

P. – ?

S. – Mettons la chose autrement. S’il y avait deux pieds dans cette direction et seulement un dans celle-là, l’espace ne serait-il pas d’une fois deux pieds ?

P. – Sans doute.

S. – Mais puisqu’il y a deux pieds là aussi, est-ce que ça ne fait pas, disons, deux fois deux ?

P. – Tu parles d’or, ô Socrate.

S. – Et combien ça fait, deux fois deux ? Calcule, et dis-le-moi.

P. – À quatre pas d’ici je te le fais savoir.

S. – Ne pourrait-on pas dessiner un espace double de celui-ci mais semblable, avec tous ses côtés égaux, tout comme celui-ci ?

P. – Certes.

S. – Et il aura combien de pieds ?

P. – Huit.

S. – Essaye de me dire de quelle longueur sera chacun de ses côtés. Cet espace a un côté de deux pieds. Quel sera le côté de l’espace double ?

P. – Double.

S. – Note, Ménon, que je ne lui enseigne rien, je ne fais que lui poser des questions. En ce moment, il croit connaître la longueur du côté de l’espace de huit pieds. Ne le croit-il pas ?

M. – Mais oui.

S. – Il le croit. Mais le sait-il ?

M. – Mais non. Il croit que cette ligne a deux fois la longueur de l’autre.

S. – Bon, maintenant tu vas le voir commencer à anamnéser, se ressouvenir des choses dans l’ordre, comme on doit se ressouvenir.

Tu dis qu’un côté double produit un espace double ?

P. – Je le dis.

S. – Je parle d’un espace comme celui-ci, pas un espace long dans un sens et court dans l’autre, comme celui-là, mais un espace égal dans tous les sens, et de huit pieds de mesure. T’obstines-tu ?

P. – Je m’obstine. Oui, tout autre que moi, au seul bruit de ton nom pourrait trembler d’effroi ; les palmes dont je vois ta tête si couverte semblent porter écrit le destin de ma perte. J’attaque en téméraire un bras toujours vainqueur. Mais j’aurai cette force, ayant assez de cœur.

S. – J’admire ton courage et je plains ta jeunesse. Aurons-nous une ligne double si nous en ajoutons une de même longueur à la suite ?

P. – Nous l’aurons, je l’admets.

S. – Et c’est sur cette ligne n’est-ce pas que nous obtiendrons l’espace de huit pieds en en construisant quatre égales ? Traçons donc ces quatre lignes, en prenant la première pour modèle. N’est-ce pas ainsi qu’on obtiendra l’espace de huit pieds ?

P. – Hum !

S. – Mais cet espace-là ne contient-il pas ces quatre espaces-ci, dont chacun est égal au premier ?

P. – Je ne saurais le nier.

S. – Quelle est donc sa taille ? N’est-elle pas quatre fois plus grande ?

P. – (Il se tait.)

S. – Deux fois, est-ce la même chose que quatre fois ?

P. – Non, par Zeus !

S. – Elle est quoi alors ?

P. – Tetraplasion.

S. – Ainsi, doubler le côté ne nous a pas donné un espace double, mais un quadruple ?

P. – (Il se tait.)

S. – Et quatre fois quatre font seize, n’est-ce pas ?

P. – Percé jusques au fond du cœur/ D’une atteinte imprévue aussi bien que mortelle/ Je demeure immobile et mon âme abattue/ Cède au coup qui me tue.

…

Mais le rôle qui nous était assigné n’était guère différent, en fait, de celui attribué au « petit », interlocuteur de Socrate dans le dialogue. La simplicité apparente, la « trivialité » de surface des figures ensemblistes proposées dissimulait une vérité profonde. Une « célèbre » erreur de Lebesgue ayant supposé, faussement, que « l’image par une application d’une intersection est l’intersection des images » servait de parabole. Sans la théorie des ensembles nous risquions de tomber, nous aussi, dans les mêmes erreurs ; ou d’en commettre de bien pires. Si, comme le Petit dans la parabole platonicienne, nous nous laissions aller à notre intuition, ce serait la catastrophe. Nous nous imaginerions posséder le savoir, mais ce savoir, notre petit savoir conscient, ne serait qu’illusion, ne serait que l’opinion transmise des mathématiciens du passé. En fait, bien sûr, nous savions. Mais nous ne savions pas que nous savions.

Le savoir ensembliste était en nous. C’était le savoir mathématique le plus fondamental. Mais nous devions aller le rechercher en nous-mêmes, comme le Petit, bien guidé par Socrate, avait retrouvée l’idée enfouie de « diagonale », par anamnèse, et réminiscence ; par « réminiscience ».

17 (§ 5) pour une bonne partie d’entre eux, il se produisit une véritable conversion

Il faut ici faire une séparation, grossière mais assez opératoire, entre ce qu’on peut nommer différentes générations. Les bourbakistes, les membres du groupe des fondateurs, les apôtres de la nouvelle religion mathématique avaient été les inventeurs d’une entreprise générale assez exaltante : tout reconstruire de l’édifice mathématique, en puisant (ce sont leurs propres termes) à une « source unique », la théorie axiomatique des ensembles. Ce sont eux qui représentaient la seconde génération (je place, arbitrairement, tous les mathématiciens non « bourbakisés » dans une « première génération », faite de « vieilles barbes » ; génération dépassée (pour un bourbakisme fanatique) ; archaïque).

Or Bourbaki, ce « mathématicien collectif », comme l’appelle Raymond Queneau, avait une bonne connaissance de la réalité des mathématiques existantes au moment de la composition de son Traité ; avec, certes, quelques « trous » : les probabilités par exemple, considérées comme simple branche « appliquée » de la théorie de la mesure ; et la logique, surtout la logique, presque frappée pour lui d’interdit à cause (disait-on) de la mort prématurée d’Herbrand, qui avait été, dans la génération des fondateurs, tous normaliens, élève de Hilbert, et comme tel associé à son irrésistible essor ; la logique, en somme, s’était tuée en montagne avec Herbrand. Les bourbakistes avaient donc une conscience nette de la distance entre le « réel » des mathématiques et la présentation idéale d’une axiomatisation, même solidement bâtie comme la leur.

(Ils ne semblent pas avoir été sensibles, au moins dans les années dont je parle, à une difficulté bien plus grave : l’architecture du Traité, en effet, reposait sur l’idée d’ensemble ; non seulement sur une axiomatique rigoureuse de cette notion, mais bel et bien sur l’idée, qualifiée par Bourbaki de « naïve », de collection d’objets abstraits, simples, et sans autres propriétés intuitives que celles résultant de la relation d’appartenance qui lie entre eux deux types d’objets élémentaires : les éléments et les ensembles. D’où une extrême difficulté à modifier l’architecture du Traité, mais surtout une quasi-impossibilité à admettre et peut-être même à concevoir qu’un bouleversement des « fondations » du bâtiment pourrait devenir nécessaire.) (J’ai rencontré une impossibilité du même genre dans la poursuite de la chimère de mon Projet ; et cette impossibilité a résulté en partie de son inspiration « bourbakiste ».) (C’est vraisemblablement aussi pour cette raison qu’aujourd’hui j’éprouve une véritable allergie à fixer à l’avance les étapes de ce livre.)

La génération suivante fut celle des suiveurs immédiats, celle des convertis avec, comme chez tous les convertis, une forte propension au fanatisme. Cette troisième génération rencontra le bourbakisme sur les bancs de l’institut Henri-Poincaré (lequel Poincaré dut en frissonner d’horreur dans sa tombe), puis, peu à peu, sur ceux de toutes les facultés des sciences de France, à mesure que la vague moderniste les envahissait. Les mathématiciens de cette génération avaient nécessairement, dans leurs études pré-universitaires, rencontré, à un niveau beaucoup plus élémentaire certes, mais déjà assez bien constituée, une vision des mathématiques fort différente de celle que leur offrait Bourbaki ; et même s’ils étaient amenés à la rejeter violemment, ils ne pouvaient pas ignorer que celle qu’ils adoptaient n’était pas la seule, qu’elle en remplaçait une autre (et peut-être plus d’une en fait).

Vint enfin la quatrième génération, celle des suiveurs des suiveurs, formée par les suiveurs. Les suiveurs de suiveurs, dans toutes les situations de ce genre, ne savent plus rien de ce qui a motivé les fondateurs, ni des résidus du savoir ancien que conservent encore leurs prédécesseurs immédiats. Ils pensent savoir tout ce qu’il y a à savoir, dès les commencements. Ils pensent n’avoir qu’à poursuivre, aller plus loin dans une voie déjà entièrement tracée. Ils n’ont que ce futur en tête. Ils ignorent presque tout du passé de leur discipline, ce futur inverse aussi nécessaire que l’autre à la compréhension. Or ce sont eux, et parmi eux, bien sûr, ceux qui, pour la plupart, se contentèrent de leurs certitudes axiomatiques acquises, qui envahirent l’enseignement dans les années soixante.

En poésie, toutes proportions gardées, l’héritage surréaliste joua, et joue encore, même chez ceux qui croient en être débarrassés, un rôle semblable à celui du bourbakisme.

18 (§ 6) je m’étais dit alors : je serai mathématicien !

J’ai retenu cela ainsi (je me le suis répété souvent, comme étant la simple restitution inchangée d’un souvenir indiscutable) : « je me suis dit un jour : je serai mathématicien ! ». Dans la construction autobiographique sans cesse inconsciemment révisée à laquelle nous nous livrons tous, guère plus stable pourtant qu’une transmission de généalogies dans une société sans écriture, l’évocation de tels moments, dits décisifs, s’enrichit, d’année en année, de nouveaux détails narratifs, jusqu’à constituer une sorte de conte.

Je m’efforce de retrouver les articulations de ce conte particulier, de suivre le cheminement caché de cette « idée » soudainement apparue, « être mathématicien », et je reconnais quelques étapes, un petit nombre de « stations » spéculatives, les dernières rapidement franchies aux premiers jours de l’été de 1952, et conduisant à un changement complet de perspective vitale.

J’avais d’abord, en renonçant à la préparation au concours littéraire de l’ENS, assuré l’autonomie absolue de l’activité poétique face aux empiétements de la « dissection » critique scolaire (vieille position postromantique, rajeunie par les surréalistes et adoptée par moi, je le croyais du moins, spontanément). Je m’étais alors dirigé vers des études d’anglais, où le combat avec l’autre langue établissait une nouvelle distance, que je sentais instinctivement salutaire, avec la poésie.

Mais pourquoi s’en tenir à une seule autre langue ? Mon démon familier, la mégalomanie intellectuelle prospective, me suggéra le russe, choix peu surprenant à l’époque, la fin de la guerre encore si proche, avec le prétexte raisonnable d’une « valeur ajoutée » à mes futurs diplômes. La distance de langue y était beaucoup plus grande : à la fois parce que l’anglais appartenait à mon horizon depuis l’enfance, et parce que s’ajoutait, dans le cas du russe, à l’exotisme sonore, accentuel, morphologique (huit cas !) et syntaxique (l’étonnant « système » du verbe, l’opposition mystérieuse, en chaque idée verbale, d’un aspect perfectif et d’un imperfectif), le très grand charme de la singularité graphique.

(Comme il s’agissait d’une écriture « alphabétique », il n’y avait pas un gros effort à faire pour la maîtriser visuellement, et quelques proximités gréco-romaines dans les signes ne faisaient que mettre plus encore en relief l’originalité du « ui » par exemple, et surtout, surtout, de l’impressionnante batterie des chuintantes. Je ne pouvais découvrir sur la page le mot « chtchi » (soupe aux choux), sans entendre et voir le ronflement vague et vaste de la Volga, celle qui hante les films de Donskoï et le Klim Samguine de Gorki.)

J’avais à peine « avalé » une année de russe que mon démon, toujours le même, toujours rapidement fatigué des efforts indispensables à la mise en œuvre d’un quelconque de ses programmes merveilleux et démentiels, et par conséquent prompt à me présenter sous les couleurs les plus audacieuses les renoncements les plus lamentables (il avait à sa disposition la version « Villiers de l’Isle-Adam » : « À quoi bon réaliser nos rêves ? Ils sont si beaux » ; et la version « Gertrude Stein » : « If it can be done, why do it ? »), me fit observer qu’il y avait bien d’autres langues slaves que le russe, toute une famille en somme et que, sous le couvert d’un gain appréciable en connaissances socialement utilisables, ainsi qu’en originalité, je me devais de les entreprendre toutes. Ce fatal début d’été j’avais, aussitôt, fait l’acquisition d’une grammaire du polonais, due à Antoine Meillet.

19 (suite du § 18) Or les études de langue, à l’époque, n’effleuraient la linguistique que dans sa section « historique »

Or les études de langue, à l’époque, n’effleuraient la linguistique que dans sa section « historique », et sous les espèces d’une discipline nommée philologie. La licence d’anglais, par exemple, comportait un certificat ainsi qualifié où on s’initiait, non sans douleurs, au « vieil anglais », celui du poème de Beowulf (on en venait très vite à maudire le miracle qui vers 1700 avait fait in extremis échapper l’unique manuscrit du poème aux flammes de l’incendie de la bibliothèque « Bodléienne » d’Oxford (elles l’avaient léché à peine, s’arrêtant de justesse au moment de le consumer, effroyable sacrilège)).

On y apprenait (rapidement et succinctement, juste de quoi aiguiser l’appétit de mon démon) que le vieil anglais, langue germanique, baignait par ses ancêtres dans un « germanique commun », étrange et hypothétique, lui-même enfant tardif d’un fort mystérieux « indo-européen ». Et voilà que l’auteur de ma grammaire polonaise, aux pages à peine coupées et déjà presque banales, s’était intéressé à ce germanique et surtout, surtout, avait écrit une « Introduction à l’étude comparative des langues indo-européennes ». Ce titre sobre, majestueux et rassurant à la fois (il s’agissait d’une « introduction »), me plut. Je ne tardai pas à m’en emparer.

Je l’ouvris, et un univers enchanteur se montra à mes yeux. Comme les mesquineries du thème anglais semblaient petites et lointaines : les listes de vocabulaire à mémoriser, les expressions idiomatiques, les « faux amis »… ; broutilles que tout cela. Un monde immense s’ouvrait devant moi, que je survolais avec aisance, perché sur le tapis volant de la prose philologique générale et rigoureuse du grand Meillet, héritier de Ferdinand de Saussure et de Michel Bréhal ;

ivresse du hittite ; merveilles des distinctions subtiles en tokkarien A et tokkarien B !, ruines de langues surgies frémissantes des sables d’un désert mongoloïde pour être reconnues cousines du grec, du gaulois, du latin, de l’albanais ! Je pris une mesure prudemment rapide des principaux chapitres, sans entrer dans les détails techniques (ils semblaient ardus), mais je lus et relus bien des fois le survol général, l’introduction à l’« introduction », la description de ce paysage des mille et une nuits langagières. Ah belles langues mortes, mes parentes, comme j’aurais voulu vous comprendre toutes !

Il peut sembler curieux, dans ces conditions, que je ne me sois pas voué à un programme d’acquisition de langues étranges de cette grande famille, vives ou mortes (il m’est arrivé parfois de le regretter). Je ne sais pas trop pourquoi il n’en fut pas ainsi. Sans doute aurais-je dû faire d’immenses efforts ; sans doute n’étais-je pas prêt alors, et surtout pas acculé par une nécessité impérieuse, à faire d’immenses efforts : je ne suis pas « naturellement » polyglotte, et j’aurais été forcé de compenser mon manque de légèreté dans l’apprentissage par du labeur. Quoi qu’il en soit, et il ne me fallut pour cela qu’un après-midi, je changeai brusquement d’horizon, substituant à l’indo-européen la mathématique.

La raison raisonnable de ce changement me paraît claire. J’en ai longuement « poli », dans ma tête, le récit, avec les années. Elle s’articule en deux temps :

– premièrement, que ce qui m’attirait « réellement » dans l’indo-européen, comme dans la philologie anglaise, polonaise ou russe, n’était pas la variété chatoyante des formes langagières, les infinis accidents pittoresques de la biographie des mots et des dialectes, mais le fait qu’ils étaient soumis à des lois annoncées rigoureuses, et que ces lois, loi de Grimm en philologie germanique, principes de la palatalisation slave, responsable de toutes les belles chuintantes russes ou auvergnates…, promettaient de soumettre l’irrésistible et millénaire mouvement des langues non au hasard mais à quelque chose qui ressemblait étonnamment à un calcul ;

– deuxièmement et conséquemment que, puisque ce qu’il y avait de plus noble dans la discipline linguistique (et si j’avais connu alors la phonologie de Troubetzkoï et Jakobson, la conclusion aurait été plus évidente encore) était son pouvoir de déduction, il y avait quelque chose de plus noble encore qui était le terrain d’application de la déduction pure, la mathématique donc. Et c’est pourquoi il me fallait impérativement devenir mathématicien.

20 (§ 7) il n’y avait à découvrir (et à découvrir vite) que le chemin. Je caricature à peine)

Cette idée assez puérile venait, plus décisivement que du cycle secondaire des lycées, de leurs classes préparatoires. Dans ces enclaves intellectuellement surchauffées, la difficulté des problèmes posés aux élèves, entraînement quasi sportif aux épreuves des grands et moyens concours, qu’il faudrait résoudre, le jour venu, plus vite et plus ingénieusement que les autres (les rivaux pour l’acquisition des places convoitées à l’X, aux Mines ou aux Écoles normales supérieures de tous calibres), créait inévitablement (on pourrait mettre ici le présent ; les conditions ont à peine bougé) un sentiment d’admiration pour ceux qui en étaient le mieux capables. En fait, elle marquait ces jeunes esprits de manière indélébile pour le reste de leur existence.

Les conséquences n’en étaient (n’en sont) pas limitées à ce contresens élémentaire sur la nature de la recherche en mathématiques que j’ai noté : qu’on doit simplement, quoique, bien sûr, difficilement, aller, démonstrativement, de l’état A (ce qui est acquis et bien connu) à l’état B (le théorème à démontrer, dont on connaît déjà la nature, et même l’énoncé). Confrontés aux mathématiques réellement existantes, les brillants sujets devenus aspirants mathématiciens devaient sans trop tarder abandonner cette conception. Il reste que l’idée antérieure demeurait en eux, à peine travestie, transposée plus ou moins inconsciemment aux mathématiques de découverte. C’est elle qui inspire le dicton fameux, répété à satiété par les plus éminents bourbakistes et repris par leurs émules : « L’honneur du mathématicien est de démontrer des théorèmes. »

La dimension éthique, d’une éthique assez médiévale, évoquant les chevaliers, les tournois et les duels au sens « Alexandre Dumas » du mot, n’est pas la composante la moins importante de cette proposition. Elle implique, par exemple, que ceux des mathématiciens qui ne démontrent pas de théorèmes, ou seulement des théorèmes peu dignes, par leur faible difficulté, par leur moindre résistance aux efforts des prédécesseurs, d’être considérés comme de « vrais » théorèmes, ont peu d’honneur mathématique, ou peut-être même pas d’honneur du tout. (→ Bif. A)

Voilà qui aurait réjoui le cœur de l’inventeur du zéro, si tant est qu’il ait pu comprendre une telle « pensée », ce qui est peu vraisemblable.

Une idée connexe, particulièrement influente dans l’« école française », était que le « champion mathématique » était par essence seul avec ses créations. Sa valeur était strictement individuelle. C’est seul qu’on triomphe dans les épreuves initiatiques, seul qu’on recevra la gloire mathématique pour le « résultat » de ses recherches (pas de copie collective au concours de l’X).

La même vision, enfin, justifiait cette bizarrerie (du moins je la sentais telle) de l’établissement, dans le consensus des professeurs et élèves, d’une stricte hiérarchie parmi les branches des mathématiques qui, en termes élémentaires, accordait une supériorité intrinsèque à la géométrie sur l’algèbre, mais laissait par ailleurs une place à part à l’inclassable arithmétique, sentie comme une espèce mystérieuse de poésie.

21 (suite du § 20) C’est sous l’éclairage précédent que je me permettrai d’interpréter cette autre formule

C’est sous l’éclairage précédent que je me permettrai d’interpréter cette autre formule, souvent citée avec componction par les bourbakistes, et attribuée à Dirichlet (je cite comme je me souviens en ce moment) : « Les grands mathématiciens ont, de tout temps, été ceux qui ont su substituer les idées au calcul. » Rien d’offensant, à première vue, dans cette sentence, qui pourrait même paraître un truisme. Mais, si on laisse de côté l’esprit dans lequel Dirichlet l’énonça initialement, et les circonstances particulières de sa remarque, qui sont d’intérêt purement historique, elle marque, dans son utilisation insistante et anachronique, un mépris certain pour le calcul (et je ne pense pas ici au calcul numérique ou automatique, à l’opposition banale entre mathématiques pures et appliquées), en fait, une dévalorisation nette de l’algèbre.

Elle exprime la conviction profonde que ce qui est mécanique, mécanisable est en fait sans valeur intrinsèque, n’a pas, au fond, de sens mathématique. Elle ignore que bien des idées naissent du calcul, sans aucunement se substituer à lui, mais l’accompagnant au contraire, pour ne recevoir de force que de nouveaux modes de calcul. Elle « oublie » que, plus significativement encore, le calcul a ce pouvoir, thérapeutique, de faire apparaître bien des idées en apparence profondes, originales, dignes, comme des chimères, des fantômes, des illusions. On pourrait, en fait, soutenir la thèse qu’il n’y a d’idées mathématiques qu’ultimement « calculables ».

De ce dédain du calcul, de l’algèbre, procède aussi la réticence (c’est le moins qu’on puisse dire) du milieu mathématique, ce pays habité par ceux que les Anglo-Saxons appellent les working mathematicians, dont les suffrages sont si nécessaires à l’acceptation d’une théorie nouvelle, d’un point de vue nouveau sur les objets dont ils s’occupent, théories et points de vue toujours sommés de répondre avant tout à la question cruciale : « à quoi ça sert ? », pour les aspects formels et calculatoires de la logique, pour le « calcul des prédicats » par exemple, plus généralement pour tout ce qu’on qualifie, de manière clairement péjorative, de « syntaxique », et qu’on oppose, à son détriment, à ce qui seul a de la noblesse, le « sémantique ».

Particulièrement répugnante au working mathematician a été très longtemps l’idée que le processus de démonstration, l’essence même de ce qui fait, depuis les Grecs (et sans modifications, pensait-on), l’originalité irréductible de la mathématique, pouvait être rendu calculatoire lui-même ;

sauf dans un rôle strictement délimité et subalterne : celui de contribuer à défendre la mathématique contre l’incertitude, contre tous ces obscurs paradoxes du début du siècle vingtième qui avaient posé la question, embarrassante mais pensée, au fond, et de plus en plus, comme tout à fait secondaire, des « fondements ».

(Le « Traité », reflet naïf de cette conviction intime, tenta ainsi, dans un chapitre introductif au livre de Théorie des ensembles (chapitre qui fut objet de remarques sarcastiques de la part des logiciens), de se débarrasser une fois pour toutes de ces questions largement secondaires, écartées par ailleurs, en quelques phrases dédaigneuses et sereines, comme dépassées, dans l’exposé majestueux des motifs de l’entreprise.)

22 (§ 7 & § 8) la discipline, la rigueur, la sévérité du calcul semblaient pouvoir servir d’isolant intellectuel, et même de protection (pour un être doué de raison calculatoire)

Le calcul algébrique élémentaire m’avait toujours plu, et c’est sa discipline que je cherchais en priorité dans la « taupe ». C’était un jeu, aux règles bien définies, et qu’on jouait avec ce qui était le plus proche pos sible des nombres, avec des symboles se substituant à eux. J’aimais les « identités remarquables », j’adorais le triangle de Pascal, les coefficients du binôme de Newton, les « sommes » fascinantes qu’on en déduit par de point trop ésotériques manipulations. Les équations algébriques des troisième et quatrième degrés avec leurs « résolvantes », l’impossibilité de la résolution de l’équation générale du cinquième degré (et au-delà) par « radicaux », les relations « familiales » entre coefficients et racines, voilà les questions que j’aurais voulu voir abordées d’une manière beaucoup moins sommaire que ne le permettait le programme des concours.

C’est bien d’ailleurs, toujours, dans l’algèbre que je me suis senti mathématiquement à l’aise, une fois surmontée l’épreuve, difficile, de pénétration des modes axiomatiques de raisonnement : algèbre des groupes et des anneaux, des algèbres et des modules, si différente en apparence pourtant de l’algèbre élémentaire des lycées. Et j’ai été, malheureusement seulement vers la fin de ma préoccupation la plus intense pour les affaires de la mathématique (vers 1970), jusqu’au bord de la compréhension du grand théorème de classification des groupes finis, le fameux théorème de Feit & Thompson, dont la démonstration, dans un numéro à lui consacré entièrement du Pacific Journal of Mathematics, est un raisonnement par l’absurde poursuivi sur plus de 400 pages ! Comme l’écrit Bourbaki dans l’Introduction de son livre d’Algèbre : « Faire de l’algèbre, c’est essentiellement calculer… »

Moins directement et plus généralement d’ailleurs, les déductions léchées du Traité, avec la minutie de leur présentation, l’effort constant d’un découpage des chaînes déductives en pas à peu près triviaux (quand on était devenu assez habitué à ce mode de progression pour les reconnaître tels), la précision pédante et suraffichée des définitions, propositions, lemmes, théorèmes et corollaires, les renvois incessants, chiffrés, typographiquement marqués, aux résultats et notions antérieurement introduits et nécessaires à tel moment d’une démonstration, résultat, comme je l’appris plus tard, de nombreuses rédactions reprises, critiquées collectivement et corrigées d’édition en édition en vue d’atteindre à des sommets infranchissables de netteté, de clarté et de conviction pédagogiques (au point de finir par tomber, par une surenchère permanente de rigueur et de perfection, dans une obscurité d’ordre supérieur), allaient devenir pour moi et rester de longues années comme une espèce nouvelle et irrésistiblement séduisante de calcul.

Les successions calculatoires de l’algèbre ou de l’axiomatique, bien décidées, irréductibles, nécessaires, ne détruisaient pas en fait toute rêverie mathématique : imaginations de théorèmes, conjectures, pressenti ments de résultats non encore énoncés ou même prévisibles. Mais elles impliquaient une double discipline, au fond assez rassurante : ne rêver qu’à partir d’elles, et revenir à elles toujours. Elles donnaient de la certitude.

Surtout pas d’ailleurs une certitude personnelle, originale ; bien au contraire, la certitude d’être dans le certain collectif, universel, partageable. En cas de doute, cette certitude pouvait toujours être reconquise, et les erreurs du rêve, de l’intuition irresponsable, corrigées, par le coup de règle sur les doigts de la conséquence fausse surgie au bout du raisonnement, toujours de la même manière : en revenant en arrière, en recommençant les mêmes calculs, les mêmes enchaînements d’implications. Il fallait de la patience, de l’obstination ; il fallait du temps. La récompense était une sorte d’apaisement.

Il en résulte que c’était bien l’algèbre, en ce sens un peu exagérément étendu, qui m’attirait vers la mathématique, pas la géométrie. Car la géométrie était trop assimilable pour moi à la physique (c’est une idée qui a été philosophiquement défendue). J’y percevais trop, dans ma myopie à la fois naturelle, faiblesse de mon esprit, mais aussi en partie volontaire, quelque chose comme un recours à des données beaucoup trop extérieures à la manipulation stricte des symboles, nécessitant une appréhension par intuition. Ce don d’intuition, de divination géométrique, intransmissible (que mon ami Jean Bénabou possède à l’évidence, et que j’ai vu brusquement apparaître, au beau milieu de sa classe de seconde, sans que rien au préalable ne l’ait laissé prévoir, chez Charlotte, ma seconde fille (et il fut par conséquent d’autant plus frappant pour moi de constater la réalité de ce type d’intuition, puisque à l’état non élaboré, comme un métal en quelque sorte natif, et pur)), ce don, je ne l’ai pas.

23 (suite du § 22) Je cherchais le calcul.

Je cherchais le calcul. Pour me protéger ; mais de quoi ? J’aurais vraisemblablement répondu alors : du vague, de l’absence de rigueur, de la « littérature » (au sens péjoratif de ce mot). (Si je donne une autre interprétation, beaucoup plus détaillée, raisonnée, articulée à ma démarche de 1952, c’est en effectuant de manière volontaire, consciente, « cynique », ce que notre mémoire fait automatiquement à tout moment en ramenant à nous ce que nous prétendons être le passé : une constitution d’événement historique, bien plus qu’une reconstitution. Je ne répéterai pas toujours un tel avertissement à ne pas lire ce que j’écris comme la revendication d’une restitution fidèle du passé ; parfois seulement, quand j’en sentirai le besoin, je l’indiquerai d’une flèche tracée dans la ligne, orientant le lecteur vers ce « moment » de prose, et de prudence.)

Ma méfiance envers la géométrie et tout ce qui, dans la mathématique, avait besoin des mêmes qualités intuitives, née d’une incapacité plutôt que d’une réflexion justifiée, était aussi une transposition : de la poésie vers la mathématique. Formé d’abord au vers régulier, je m’étais enthousiasmé, comme tout le monde, pour le vers-librisme torride des surréalistes et de leurs émules.

Or cette liberté formelle, considérée comme indissociable de la liberté tout court, tout en ne m’étant pas apparue encore comme une simple soumission aux formes les plus mécaniques des influences héritées, me gênait. J’y étais de moins en moins à l’aise.

Et j’avais conclu de cette gêne, de cette insatisfaction de plus en plus paralysante, qui m’ôtait jusqu’à la joie de composer de la poésie, que ce dont j’avais besoin impérieux (à satisfaire immédiatement, au nom des intérêts supérieurs de mon existence future : je voulais être poète, n’est-ce pas ? Je ne voulais rien plus intensément), c’était de m’isoler le plus absolument possible de mon environnement poétique, recherche un peu comparable à celle de Stendhal dans la prose du Code civil, cette algèbre juridique.

Mon état de désolation, presque de honte, au moment dont je parle dans ce chapitre, était dû au fait qu’apparemment tout ce bouleversement dans ma trajectoire universitaire n’avait servi à rien, ne m’avait pas donné le salut poétique ; et dans la mathématique, j’étais perdu.

Pourtant, mais je ne le découvris que plus tard, je tenais là le remède à la « crise de poésie » où j’étais enfoncé dans ces années, et où m’avait jeté mon adhésion adolescente au modernisme surréaliste et dans une plus grande mesure encore (en me coupant en fait la voie d’un retour au vers traditionnel (en poésie « one never changes back »)) à sa correction « réaliste-socialiste ».

24 (§ 9) Tout immergé dans la fraîcheur, face au ruissellement d’étincelles du bassin,

Je sors mon petit carnet noir à rayures obliques jaune-orange (le voici, sur mon bureau, au pied de l’écran) acheté dans la papeterie de l’île de la Cité qui se trouve à quelques pas de la statue d’Henri IV (et où je me fournis principalement en « chemises » de couleurs différentes destinées à recevoir un jour, quand j’aurais le temps (jour sans cesse reculé vers un futur plus opportun), la totalité de mes papiers, en les distribuant de manière adéquate selon différentes rubriques sémantiquement identifiables d’un coup d’œil par la couleur de la chemise qui les contiendra : du rouge pour les mathématiques, du bleu pour la poétique, du vert pour la prose…).

Je sors ensuite de la poche droite de mon pantalon le porte-cartes (le voilà) qui contient notamment ma « carte bleue Visa », ma carte de la Bibliothèque nationale ainsi que celle de la Sorbonne (j’en passe et des meilleures), et du porte-cartes ce merveilleux bi-stylo plat (admirez-le), un cadeau de Marie lors d’un séjour à Londres (la plus grande partie de nos séjours à Londres se passe, quand nous ne sommes pas au « pub », soit aux « puces », à Camden Lock, à Petticoat Lane ou à Portobello Road, soit dans les papeteries), avec lequel je me propose de prendre les notes préparatoires à la composition de l’hommage oulipien à mon ami Jean Bénabou à l’occasion de son soixantième anniversaire, que j’ai l’intention de présenter le lendemain.

(C’est-à-dire aujourd’hui.) (C’est-à-dire que ceci a été composé le dimanche, est une « prose orale », encomiastique, qui fut effectivement prononcée le soir même dans un appartement de cinquième étage au coin de la place Denfert-Rochereau, après l’extinction des bougies.)

Nous sommes donc (écrivais-je le dimanche matin, disais-je le dimanche soir) le samedi 23 mai 1992.

Mais, me direz-vous, pourquoi avoir abandonné le confort d’un bureau et d’un écran de Macintosh LC pour un banc austère des Tuileries et le spectacle distractif des carpes et des canards ? C’est très simple. C’est le samedi matin que Christine, technicienne de surface du 51 rue des Francs-Bourgeois, Paris quatrième, où habitent Marie, Charlotte et Ophélie, chatte, quand elle n’est pas auprès de son vieux père (au Togo sinon au Burkina Faso), s’efforce de mettre un semblant d’ordre chez moi, 82 rue d’Amsterdam, Paris neuvième.

Elle ouvre la porte avec sa clef, elle me dit : « Bonjour Jacques. » Je réponds : « Bonjour Christine. » J’enregistre ce que j’étais en train de composer, j’éteins le Macintosh, je prends mes affaires, les place dans mon « Big Shopper », et je m’en vais. Il est impossible, chez moi, de faire marcher dans le même temps un Macintosh et un aspirateur. C’est l’heure de l’aspirateur. Je lui cède la place.

25 (suite 1 du § 24) Marcel, l’autre jour, au téléphone, m’a dit :

Marcel, l’autre jour, au téléphone, m’a dit : « Et si on lui offrait quelque chose d’oulipien ? » (Marcel Bénabou, membre de l’OULIPO et éminent historien, est un cousin de Jean.) « Excellente idée » répondis-je (Marcel a toujours d’excellentes idées). « Et quelle contrainte ? interrogeai-je. – Eh bien, tu sais, la contrainte habituelle. – Tu as raison, repris-je, on n’a pas vraiment le temps de faire autrement. »

« C’est ce que j’ai pensé » dit Marcel qui n’a en effet pas beaucoup de temps à lui puisque, non seulement il consacre à l’université à peu près dix fois plus d’heures que la quasi-totalité de ses collègues les plus consciencieux, s’occupe, avec les scrupules qu’on lui connaît, du secrétariat définitivement provisoire (ou provisoirement définitif et réciproquement) ainsi que des archives et des finances de l’Oulipo, l’Ouvroir de Littérature Potentielle, fondé par François Le Lionnais et Raymond Queneau, dont nous avons l’honneur d’être tous deux membres, mais, en plus, après n’avoir écrit aucun de ses livres il s’est mis brusquement à les écrire tous (ou presque).

Hier matin, donc, aux Tuileries, j’ai sorti mon petit carnet noir à rayures orange (obliques) et mon stylo plat et j’ai commencé par le commencement. J’ai entrepris l’établissement des listes préliminaires : liste des signes disponibles selon la contrainte, liste des mots-outils utilisables, des constructions syntaxiques envisageables, des mots significatifs surtout, ces mots propres à condenser l’essentiel du sens de l’œuvre (plus exactement ce que Chrétien de Troyes appelle le « sen »), dont je prévoyais qu’elle aurait à réunir, sous la « molt belle conjointure » (toujours Chrétien de Troyes) d’une constellation d’images saisissantes et allusives, une héroïne, Dame Théorie des Catégories, et son champion, le Chevalier Bénabou (Jean).

J’ai échoué lamentablement.

Disons que c’est faute de temps.

Au bout d’une demi-heure de rumination vague, ponctuée de temps à autre par la lecture de quelques lignes du Times, qu’après quelques semaines d’interruption j’ai recommencé à acheter (pour punir les Anglais de leur comportement lors des dernières élections à la Chambre des Communes, que je n’approuve pas, j’avais décidé de ne plus le lire ; mais Marie m’a fait observer (constatant par ailleurs la détérioration évidente de mon humeur), que c’était plutôt moi (entre autres) qui était puni par cet acte politiquement courageux, certes, mais somme toute peu efficace), je n’avais en tout et pour tout à ma disposition que deux mots, le second d’ailleurs un mot anglais (dont, pour comble d’infortune, j’avais oublié le sens !) :

1° banjo

2° jejune (ennuyeux, plat, dit le Robert & Collins)

Que faire ?, comme disait Lénine en son temps.

26 (suite 2 du § 24) Que faire ?, comme disait Lénine en son temps.

Non seulement c’était peu, non seulement leur utilisation paraissait pour le moins problématique, mais ils me semblent témoigner, après coup, maintenant que j’ai retrouvé le sens du second, d’un certain pessimisme spontané de mon esprit devant l’ampleur de la tâche qui m’attendait et dans laquelle je m’étais, sans réfléchir suffisamment, engagé (« c’est la faute à Marcel » pensai-je).

Le seul fragment convenable, adéquat, auquel je sois parvenu étant celui qui donne maintenant son titre à ceci que je suis en train de vous lire, le mieux est que je vous livre les données brutes, extraites des pages de mon carnet, qui reflètent assez fidèlement la chronologie de mon labeur.

Vous pourrez considérer ces bribes comme des matériaux qui vous permettront, je l’espère, de mener à bien l’entreprise interrompue (« la poésie », n’est-ce pas, a dit un célèbre « retraité de l’administration » (peut-être « Contrôleur des poids et mesures »), M. Ducasse, « doit être faite par tous, non par un »). (Je profite de l’occasion pour faire remarquer à M. Ducasse que la poésie est nécessairement « faite par tous », parce qu’elle est langue, et non par un, en tant qu’elle refléterait une biographie ; c’est pour cette raison aussi qu’elle est « ininterrompue », sauf par la mort (de la langue).)

– Voici donc :

banjo jejune jeune, jeûne, à jeun, je

boue, bouée, boubou, joue, bajoue, noue, noué, nouba, nô, Noé, néon, neu-neu (séquence découverte rapidement)

nu, nuée,

eau

naja, nana, nanan

onu, noon, nonne, none

ô, au, on, ne, né, en, éon, eu, eue

aube une aube ? : beau !

un beau jeu, un bon jeu, un enjeu enjoué

un an, une bonne année, Anne, Anna, on bée, Énée, abonné, non ! non ! (crise d’inspiration un peu désordonnée !)

ébène

nabab, baobab, boa, Banon, jojoba, jubé (encore un mot dont j’ignorais le sens ; heureusement Florence m’a donné (non, prêté) un portrait de jubé, celui de Saint-Étienne-du-Mont (1521-1545), que voilà devant vous, en carte postale)

bab, bébé, bobo, bubu (Bubu de Montparnasse ? ou « Bubu », petit nom de Buxane, sable-collie de ma nièce Marianne ?), bonbon, bonbonne

jujube

jab

abbé jaune, béjaune joe, jojo, joujou

na !

299 JXT, 75, rue de Rivoli, 23/05/ 11 heures. (Excusez-moi, ceci n’a rien à voir avec la contrainte. Il s’agit d’un numéro d’immatriculation parisienne. Je collectionne les immatriculations. Plus exactement, je cherche les numéros les plus récents. Cela me permet de garder un certain contrôle mental sur les automobiles, ces ennemis mortels du pié ton. Je vois passer une voiture terriblement neuve, et je me dis : « Mais tu n’es pas la plus neuve ! pauvre idiote, il y en a 3, 4, 5000 après toi ! » J’ai une autre stratégie. Je me chante intérieurement la chanson que j’ai composée à leur intention, le Chant de guerre des automobilistes parisiens : « Brûlons un feu, brûlons-en deux/ Pour affoler les petits vieux/ À la santé des Pomp’s funèbres/ Et merde pour ces cons de piétons/ À qui la guerre nous déclarons ! ») (Charlotte ne pense pas que j’arriverai au top 50 avec cette chanson. Non qu’elle me désapprouve (pas plus d’ailleurs que Laurence, qui fait son stage d’interne à l’hôpital de la prison de Fresnes), mais les épreuves des concours de l’agro, de l’ENS section C (biologie), ne lui laissent pas toute la liberté d’esprit nécessaire pour s’occuper de ma carrière de chanteur.)

Le dernier mot de ma liste (sur le chemin du retour), fut :

Ob (fleuve de Sibérie)

C’est tout ! (Ce fut tout. Nul n’avait identifié la contrainte. L’oralité ne facilite pas le déchiffrement des contraintes littérales. C’en était une. Elle est simple. Après moi, Marcel a offert quelques aphorismes adaptés à des noms de mathématiciens. Le premier, excellent à mon jugement, était :

Nul n’est censé ignorer Galois.)