‌Chapter 6

Music of the Spheres

May not music be described as the mathematics of the sense, mathematics as music of reason? The musician feels mathematics, the mathematician thinks music: music the dream, mathematics the working life.

– James Joseph Sylvester

Music, at its very core, is mathematical. It’s often said that mathematics is a universal language that could be used as a first means of communication between intelligent species on different worlds. But that claim of universality might also apply to music and, in fact, we’ve already sent some of our music towards the stars in the hope that beings out there might hear it and so come to understand something of the creatures who made it.

Voyager 1, launched on September 5, 1977, recently became the first human-made object to enter interstellar space. Having flown past Jupiter and Saturn, it headed out of the solar system and in 2012 passed beyond the heliopause, the boundary where the influence of the Sun’s magnetic field ends and that of the rest of the Galaxy begins. Its sister craft, Voyager 2, launched in the same year, is also heading for the void between stars but in a different direction. Both remain in contact with Earth, sending back data from a handful of science experiments that their dwindling power reserves can supply, but neither is destined for any close encounters with another star system in the foreseeable future. Their speed is so low compared with the immensity of interstellar distances that it would take them tens of thousands of years to reach even the nearest star, Proxima Centauri – assuming they were heading directly towards it (which they aren’t).

According to NASA’s current estimates, Voyager 1 will come within 1.6 light-years of the star Gliese 445 and Voyager 2 within 1.7 light-years of Ross 248 about 40,000 years from now. By the time of these very remote flybys both probes will be long dead. But structurally the Voyagers could remain intact for millions of years, drifting through the Milky Way galaxy and – who knows – possibly be found by some advanced race that would be curious about the probes’ origins and creators. In that unlikely event each spacecraft carries a message in the form of a gold-plated copper phonograph record containing sounds and images intended to portray the variety of life, environments, and human cultures on Earth. As well as 116 pictures, a variety of natural sounds, and spoken greetings in 57 different languages, the Voyager Golden Record features 90 minutes of music from different ages and regions of the world, including passages from Stravinsky’s The Rite of Spring, a gamelan piece from Indonesia, Bach’s Brandenburg Concerto No. 2, and Chuck Berry’s ‘Johnny B. Goode’. Thoughtfully, a stylus and coded instructions are provided by which to play the record. But, assuming aliens ever found one of the Golden Records and managed to play the music as intended, the question is whether they’d recognise it for what it is. And, similarly, if alien music somehow reached our ears, would we appreciate it as being musical?

The Voyager Golden Record.

One of us (David) is a singer and songwriter whose album Songs of the Cosmos combines science with music in tunes such as ‘Dark Energy’. But as well as songs with a scientific flavour, there’s also science in the making of music, and mathematics, deeply rooted, in the relationship between notes and the construction of scales.

It was the ancient Greeks who first discovered that there’s a strong link between music and mathematics. Pythagoras and his followers, in the sixth century bc, built an entire cult around their belief that ‘all is number’ and that the whole numbers were especially significant. Each of the numbers 1 to 10, they held, had a unique significance and meaning – 1 was the generator of all other numbers, 2 stood for opinion, 3 for harmony, and so on, all the way up 10, which was the most important and known as tetraktys because it is the triangular number made from the sum of the first four numbers, 1, 2, 3, and 4. Even numbers were considered to be female, and odd numbers male. In music, the Pythagoreans delighted in their discovery that the most harmonious sounding intervals corresponded with whole number ratios. The very same numbers they held in such high esteem on an intellectual level determined, as simple fractions, what set of notes was most satisfying to the ear. A vibrating string held down at its halfway point (2:1) sounds an octave higher than when open. Held down and played so that the length of the vibrating section to the entire string is in the ratio 3:2 gives a perfect fifth (so called because it is the fifth note in the scale and highly consonant with the root note). Likewise 4:3 produces a perfect fourth and 5:4 a major third. Since frequency depends on one divided by the string length, these ratios also give a relationship between the frequencies of the notes.

The simplest of the ratios (apart from the octave) – the perfect fifth – is the basis for what’s become known as Pythagorean tuning because modern musicologists ascribe its origins to Pythagoras and his brotherhood. Start with a note such as D and move up by a perfect fifth and down by a perfect fifth to produce other notes of the scale, A and G, respectively. Now move up another perfect fifth from A and down another perfect fifth from G to generate the next notes, and so on. Eventually, we end up with an 11-note scale centred on D like this:

E♭–B♭–F–C–G–D–A–E–B–F♯–C♯–G♯

Without some adjustments this would span a wide frequency range, equivalent to 77 notes on a piano. To make the scale more compact, low notes are shifted to a higher octave, by having their frequencies doubled or quadrupled, and higher notes are similarly shifted downwards by an octave or two. The result of bringing the notes closer together in this way is what’s called the basic octave. Pythagorean tuning was used by musicians in the West until about the end of the fifteenth century, when its limitations for playing a wider variety of pieces became apparent.

So enamoured were the Pythagoreans with their discovery – that simple ratios of vibrating strings equated to harmonious musical intervals – and their belief that the universe was based on whole numbers, that they saw a perfect marriage of music and mathematics in the heavens. At the centre of physical space, according to their cosmology, was a great fire. Around this, carried on transparent celestial spheres and moving in circular paths were 10 objects, in order from the centre: a counter-Earth, Earth itself, the Moon, the Sun, the five known planets or ‘wandering stars’ (Mercury, Venus, Mars, Jupiter, and Saturn), and, finally, the fixed stars. The separations between these spheres, they taught, corresponded to the harmonic lengths of strings, so that the movement of the spheres gave rise to a sound (inaudible to human ears) known as the ‘harmony of the spheres’.

Both the Greek words harmonia (meaning ‘joint’ or ‘agreement’) and arithmos (‘number’) come from the same Indo-European root ari, which also crops up in English words such as ‘rhythm’ and ‘rite’. Harmonia was also the Greek goddess of peace and harmony – fittingly, since her parents were Aphrodite (goddess of love) and Ares (god of war). The Pythagorean idea that musical harmonies were inherent in the spacing of heavenly bodies persisted throughout the Middle Ages. The philosophy of Musica Universalis (‘universal music’) found its way into the quadrivium, a quartet of academic subjects, including arithmetic, geometry, music, and astronomy, that was taught after the trivium (grammar, logic, and rhetoric) in medieval European universities and was based on Plato’s curriculum for higher education. At the heart of the quadrivium was the study of number in various forms: pure number (arithmetic), number in abstract space (geometry), number in time (music), and number in both space and time (astronomy). Following the lead of Pythagoras, Plato saw an intimate connection between music and astronomy: music expressing the beauty of simple numerical proportions to the ears, and astronomy to the eyes. Through different senses, they expressed the same underlying unity based on mathematics.

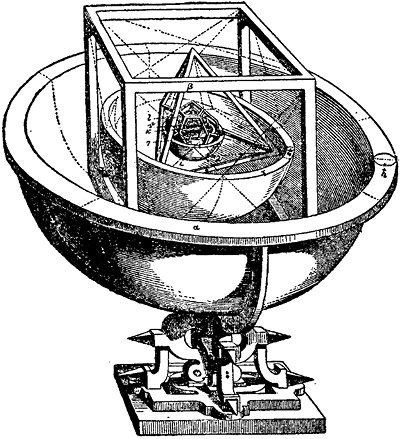
Kepler thought that the orbits of the then-known planets were spaced to match a nesting of the Platonic solids.

More than two thousand years later, the German astronomer Johannes Kepler took the notion of a musical cosmos a step further, by linking together fundamental shapes and melodic sounds across the heavens. Kepler believed in astrology and was devoutly religious, as were many other intellectuals of his time, but he was also a key figure in the scientific revolution of the Renaissance. He’s best remembered for his three laws of planetary motion, built on the foundation of accurate observations of the planets by the Danish nobleman Tycho Brahe. Early in his career, Kepler was fascinated by the notion that there might be a geometric basis to the spacing of the planets. To the Sun-centred model of the solar system proposed earlier by the Polish astronomer Nicolaus Copernicus, Kepler, in his 1596 Mysterium Cosmographicum (‘The Cosmographic Mystery’), added the idea that the five Platonic solids – the only regular, convex polyhedrons in 3D – held the key to the spacing of worlds. By inscribing and circumscribing with spheres these solids in a certain order – octahedron, icosahedron, dodecahedron, tetrahedron, and cube – Kepler believed he could generate the orbs within which the six known planets (Mercury, Venus, Earth, Mars, Jupiter, and Saturn) moved. God, it seemed, might not be a numerologist, as the Pythagoreans believed, but a geometer.

Going beyond mere speculation, Kepler carried out acoustic experiments at a time – the dawn of the seventeenth century – when testing ideas in practice was still a novel concept in academic circles. Using a monochord, he checked the sound made by the string when stopped at different lengths, and established by ear what divisions were most pleasing. As well as the fifth, which was of all-consuming importance to the Pythagoreans, he noted that the third, the fourth, the sixth, and various other intervals were also consonant. He wondered if these harmonious ratios might be reflected in the heavens, so that the old notion of the harmony of the spheres might be brought up to date and more in line with the latest observations. Perhaps the ratio of the greatest and least distances between planets and the Sun matched some of the consonant intervals he’d found. But, no, they did not. He considered then the speed of the planets at the points of maximum and minimum distance, where he knew, from observations, that they moved the slowest and the fastest, respectively, in relation to the Sun. Movement, he noted, would be a better analogue than distance to the vibration of a string and, indeed, using this planetary property, he found what seemed to be a connection. In the case of Mars, the ratio of its extreme orbital speeds (measured in terms of angular motion across the sky) was about 2:3, equivalent to a perfect fifth, or ‘diapente’ as it was known until the late nineteenth century. The extreme motions of Jupiter differed by a ratio of about 5:6 (a minor third in music) and those of Saturn by very close to 4:5 (a major third). The corresponding ratios for Earth and Venus were 15:16 (roughly the difference between mi and fa) and 24:25, respectively.

Encouraged by these correspondences, which, as it turned out, were fortuitous, Kepler went in search of more subtle cosmic harmonies. He looked at the ratios of the speeds of neighbouring worlds and convinced himself that harmonious ratios underpinned not only the movement of planets individually but also how they moved relative to one another. All of these thoughts on the subject he wrapped into a grand unified theory of how consonant intervals in music were linked to movements in the heavens, and published it in his magnum opus, Harmonices Mundi (‘The Harmony of the World’), in 1619.

Shortly after, he made a discovery that today is known as his third law of planetary motion. He found a precise connection between the time it takes a planet to go once around the Sun and its distance from the Sun, namely: the square of a planet’s period is proportional to the cube of its semi-major axis. This is the relationship still taught in physics classes today but it was uncovered originally during the course of Kepler’s mystical studies into the harmonic structure of the cosmos.

Kepler helped propel astronomy into the modern era with his crucial insight that the orbits of planets aren’t circular, as the ancients had believed, but elliptical. This paved the way for Newton’s universal theory of gravitation but, less obviously, it set the stage for innovative and more flexible systems of tuning in music. From his experiments in auditory space, Kepler wondered if there was a smallest interval – a lowest common factor – from which all other harmonies could be built. He found that there wasn’t. Just as planetary orbits weren’t based on perfect circles, there was no neat and simple way to achieve musical consonance using one fundamental interval. This became most obvious when any attempt was made to change the key of a piece of music.

Pythagorean tuning, based on stacked fifths, is one example of what’s called just tuning, in which the frequency of notes is related to ratios of reasonably small whole numbers. If we take the scale of C major, for example, divide it up into eight pitches (CDEFGABC), and give the tonic or root note, C, the ratio 1:1, and the fifth, G, the ratio 3:2, in Pythagorean tuning the notes above C have the following frequency ratios relative to C: D 9:8, E 81:64, F 4:3, G 3:2, A 27:16, B 243:128, C (one octave up) 2:1. This arrangement works fine providing we stay in the same key or use flexible instruments, such as the human voice, which can make fine adjustments to intonation on the fly. But any form of just tuning runs into problems with instruments like the piano, which, once tuned, can only produce certain frequencies.

Composers and musicians, earlier than Kepler, had started to break out of the rigid confines of Pythagorean tuning. But it was around Kepler’s time that the first important moves, in Europe at least, were made away from the notion of just tuning altogether. A pioneer of the new trend was Galileo’s father, Vincenzo Galilei, who advocated a 12-tone scale based on what became known as equal temperament. In this system, every neighbouring pair of notes is separated by the same interval, or ratio of frequencies. With 12 semitones, or half-steps, the width of each successive interval increases by a factor of 2^1/12 or 1.059463. For example, think about the scale that starts from the A above middle C, which has a frequency of 440 hertz (cycles per second) in modern orchestral tuning. The next note up is A sharp with a frequency of 440 × 1.059463, or about 466.2 hertz. Twelve intervals up from the starting note brings us to the octave with a frequency of 440 × 1.059463¹² = 880 hertz, or double the starting frequency.

Determined in this way, none of the frequencies of 12-tone equal temperament (12-TET) exactly match those of the corresponding notes in just intonation, except at the tonic and octave, although fourths and fifths are so close as to be almost indistinguishable. Equal temperament is a compromise: it isn’t as pure sounding as just intonation but it has the huge advantage of enabling music to be played that is acceptably harmonious in any key without the need for retuning. It made keyboard instruments, such as the piano, practical and musically flexible, and opened up broad new horizons in composition and orchestration.

The 12-TET is what’s used almost universally in Western music today. But in other parts of the world different systems of tuning have evolved, which is partly why the music of the East and Middle East has, to our Western ears, an exotic sound to it. Arabic music, for instance, is based on 24-TET, so that it makes liberal use of quarter-tones. However, only a fraction of the 24 tones appear in any given performance and these are determined by the maqam, or melody type, being used – comparable to how in Western music generally only 7 out of the 12 tones appear, which are determined by the key. As in Indian raga and other traditional non-Western forms, there are strict rules, even within the most elaborate and protracted improvisations, which govern the choice of notes and their relationship, together with the patterns of these notes and the progression of the melody.

From an early age, our brains become accustomed to the music that’s pervasive around us, just as they adapt to the local language, the tastes of our home food, and the ways of the people with whom we grow up. Music from other cultures may sound unusual and surprising, and, yet, for the most part, is still pleasing to the ear. The different scales, intervals, rhythms, and structures of musical pieces from other parts of the world may take some getting used to but we almost always recognise them as being musical. This is because they too are based on acoustic patterns that can be reduced to relatively simple mathematical relationships that govern such elements as melody, harmony, and tempo.

Whether the concept of music is universal is debatable. Even in the West, there have been many auditory explorations and developments, especially over the past century or so, which test the boundaries of what might be called musical. These include atonal music, which lacks the usual tonal centre, and experimental music, which intentionally breaks the customary rules of composition, tunings, and instrumentation. A pioneer of the latter was the American composer and philosopher John Cage, whose 4’33” is a three-movement piece throughout which the performer (such as a pianist) or performers (up to a full orchestra) are instructed to play nothing. The only sounds heard by the audience are whatever other sounds happen to be going on at the time – someone coughing, the creak of a chair, noises from outside. The inspiration for it came from a visit by Cage to Harvard University’s anechoic chamber, a completely echo-less room, after which Cage was moved to write: ‘There is no such thing as empty space or empty time. There is always something to hear or something to see. In fact, try as we might to make a silence, we cannot.’ Cage intended the piece to be taken seriously but, inevitably perhaps, others saw a lighter side to it. In his essay ‘Nothing’, Martin Gardner wrote: ‘I have not heard 4’33” performed, but friends who have tell me it is Cage’s finest composition.’

However we choose to define it, music isn’t exclusive to humans. Many other species make sounds that we often interpret as being musical, prominent among them being birds and whales. Masters of tuneful performances in the animal world are songbirds, of which more than 4,000 species are known, including such families as the larks, warblers, thrushes, and mockingbirds. The songs are normally sung by the male, either to attract a mate or proclaim his territory or, very often, both. Male sedge warblers, which winter in the Sahara before returning to Europe in the spring, a few days ahead of the females, sing both day and night, since their prospective partners may arrive by either, staking out and defending their territories at the same time, and then abruptly fall silent after they find a mate. Each species has a particular song, which is unvarying, although individuals can distinguish each other’s voice prints, just as human voices sound different to us even if they’re singing the same tune. The individuals of some species, such as chaffinches, have a repertoire of fixed phrases. If one chaffinch sings a particular phrase, his neighbour will answer him back with a similar phrase – a kind of echo – the purpose of which, according to one suggestion, may be that it allows the two birds to judge their distance apart.

Humpback whale breaching.

Songbirds certainly appear to be tuneful, and composers, including Vivaldi and Beethoven, have sometimes turned to them for inspiration. But whether any of their songs follow the same kind of organisational rules that humans use in their music is unclear. Some similarities are bound to happen just because of the science of acoustics and the way sounds are produced in throats and mouths. For instance, both we and the avians tend, on the whole, to use adjacent notes that aren’t widely spaced in pitch, and long notes at the end of phrases. The question is whether birds, like us, favour certain relationships between notes – definite scales – and other orderly patterns in their songs. Not much work has been done on this but one piece of research, which focused on a particularly tuneful bird, the nightingale wren of Costa Rica and southern Mexico, looked for any intervals in its songs that might correspond with diatonic, pentatonic, or chromatic scales. It found that there was no match at all other than what might be expected by chance. This doesn’t mean that the songs have no meaning – at least to other birds – just that they don’t follow Western musical scales. The fact that we find the sounds both pleasant and patterned suggests that they are music of some type, even if not of our own ilk.

The vocalisations of cetaceans, including whales and dolphins, are vastly more elaborate than anything a bird produces and are used for both communication and echolocation. The songs of the humpback whale, in particular, have been described as the most complex in the animal kingdom but they’re neither musical pieces nor conversations in the conventional sense. Each song is built up from bursts of sound or ‘notes’ that may last a few seconds, and swoop up or down in frequency or stay the same, and range in frequency from the lowest we can hear to somewhat above the highest. Also, the volume of the sound may vary over its duration. Several of these notes together comprise a sub-phrase, lasting maybe 10 seconds, and two sub-phrases combine to make a phrase, which the whale repeats as a ‘theme’ for a few minutes. A group of such themes makes up a song that may go on for half an hour or so and then be repeated over and over again for hours or even days. At any point in time, all the humpbacks in a given region sing the same song but gradually alter small elements of it, in rhythm, pitch, and duration, as the days go by. Populations of whales occupying the same geographical region have similar songs, whereas those living in different parts of the ocean, or different oceans, have totally different songs, though the underlying structure is the same. So far as is known, once a song has evolved it never goes back to the original pattern. Mathematicians who’ve applied information theory to the songs see in them a complexity of syntax and hierarchy of structure previously not encountered outside of human language. But whatever the whales are doing they’re not having regular conversations because the songs, while subtly and continually changing, are too repetitive. Think of them perhaps as being like jazz or the blues, where riffing and improvisation is allowed, even encouraged, but within well-defined guidelines. A clue to the function of whale songs is that they’re performed exclusively by males, and the most creative individuals, in terms of coming up with new variations, tend to be most successful in attracting female partners. It’s also hard to avoid the suspicion that the whales are having a great time in these collective jam sessions.

To our ears there’s a beauty and otherworldliness to whale songs that has been captured on CDs intended for relaxation and therapy. Part of a whale song, recorded by marine biologist Roger Payne using hydrophones off the coast of Bermuda in the 1970s, was placed on the Golden Records now heading towards the stars aboard the twin Voyager probes. One of those who helped produce the disc, American science writer Timothy Ferris, suggested that whale song might prove more intelligible to smart aliens than it is to us, so a lengthy piece of it was included and overlapped with greetings in various human languages. As Ferris pointed out, from an alien’s point of view: ‘It doesn’t interfere with the greetings, and if you are interested in the whale song, you can extract it.’

Music, like love and life, is hard to define. We might say we know it when we hear it, so that the definition becomes one based on personal or collective taste – a purely subjective thing. No one would seriously argue that compositions by Beethoven or The Beatles aren’t musical. But what of bird song? What of some of the artistic output of avant-garde sonic artists, like John Cage and Harry Partch, the latter who built instruments to challenge the orthodoxy of modern Western scales and harmonies? If we want an objective definition of music we must turn to the science of acoustics and the laws of mathematics, and ultimately reduce sounds, and combinations of sounds, to numbers. Again, how we choose to do this is up to us, but whatever we choose it will involve a combination of at least some of the elements without which music is impossible: melody, harmony, rhythm, tempo, timbre, and perhaps others. Once a set of criteria was selected and programmed into a computer it would be possible to analyse any sound and decide if, according to the chosen rules, it qualified as being music. The criteria could be made as inclusive or exclusive as we wanted, depending on how wide the net was to be cast, but they couldn’t be so loose as to include all sounds, or even all regular sounds. The breaking of waves on the shore is a pleasant soothing sound, and has a regular tempo, but most people would probably agree it could hardly be called musical.

Behind all music, as we normally understand it, is some kind of intelligence. It’s possible to imagine a natural system that might be able to produce truly musical passages, in the same way that certain things in nature manifest beautiful spatial forms such as a Fibonacci spiral. But nothing like that has been found to date. So far as we know, it seems that a form of brain, whether it be human, whale, bird, or computer, is needed to construct the type of sonic patterns necessary to qualify as music. Because music is fundamentally mathematical, and because mathematics, to the best of our knowledge, is universal, it seems most likely that if other intelligent species have evolved across the galaxy and beyond, then they too might have come up with music of some form. The variety is likely to be immense, just as it is on Earth. Think of a spectrum that embraces Gregorian chant, flamenco, bluegrass, gamelan, Noh, fusion, psychedelic rock, Romantic classical, and all of the other genres of music from around the world and across the ages. Now add in the possibility of new genres of which human minds have never conceived and the extent of what might comprise music across the cosmos becomes apparent. What’s more, our appreciation of music is limited by our anatomy, especially the frequency range to which our ears are sensitive, roughly between 20 hertz (cycles per second) and 20,000 hertz. Other animals can hear sounds well outside this range: down to 16 hertz in the case of elephants and up to about 200,000 hertz in some types of bat. In theory, there’s no limit to the types of sounds alien anatomies might be capable of handling, in terms of frequency, amplitude, ability to discern differences in pitch, tempo, and the like, or any other physical parameter. The processing power of some extraterrestrials may be vastly greater than that of our own brains, or that of our fastest computers, so that they can appreciate some complex sounds as being musical that would, in a sense, go over our heads.

As for the music that has been included on the Voyager Golden Records, now on their endless journeys through interstellar space, there’s been much discussion about which pieces would most obviously sound musical to alien ears. Some believe it would be the works of Bach, that most mathematical of composers. In fact, of the 27 selections of music contained on the disc, lasting a total of 90 minutes, three are by Bach – extracts from the Brandenburg Concerto No. 2 in F, the ‘Gavotte en Rondeau’ from the Partitia No. 3 in E major for Violin, and the Prelude and Fugue No. 1 in C Major from The Well-Tempered Clavier, Book 2. The Bach contributions last 12 minutes 23 seconds, or roughly one seventh of the playing time of the whole record, reflecting the belief of those who assembled the collection that the highly structured nature of Bach’s pieces, including his clever and complex use of counterpoint to interweave multiple melodic lines, would appeal to both the intellect and aesthetics of any advanced beings who came across the spacecraft.

Scientists and writers alike have pondered what extraterrestrial music might be like. In the movie Close Encounters of the Third Kind the aliens played a five-note sequence from a major scale as a greeting: ‘re mi do (down octave) do sol’. Perhaps, in the story, they did that because they’d been listening to our music and wanted it to sound familiar. Or perhaps other races across the galaxy will come up with the same musical scales as we did, because they’re the simplest mathematically and the best ones from which to make attractive melodies and harmonies, whether you grew up on Earth or the fourth planet of a star 40,000 light-years away. If mathematics is universal, then so, with many variations, may be the fundamentals of music, including similar scales and methods of tuning. There’s a certain inevitability about the development of equal temperament, for example, that may be repeated wherever intelligent beings want to be able to play a variety of different instruments and harmonise them in many different keys.

If or when humans finally make contact with another intelligence among the stars, there’s the chance it will be through music. It isn’t a new idea. In the seventeenth century, the English clergyman Francis Godwin, Bishop of Hereford, wrote a story called The Man in the Moone (published posthumously in 1638) in which his intrepid astronaut, Domingo Gonsales, encounters a race of Lunarians who communicate via a musical language. Godwin’s idea built on a description of the spoken Chinese language, with its tonal sounds, by Jesuit missionaries who had recently returned to Europe. In Godwin’s tale, the Lunarians used different notes to represent the letters of their alphabet.

In the 1960s, the German radio astronomer Sebastian von Hoerner, who wrote extensively on SETI (the Search for Extraterrestrial Intelligence), argued in favour of music as a medium of choice for interstellar communication. And it might very well be, he suggested, that alien music would have some features in common with our own. Wherever polyphonic music, in which more than one note is played at the same time, evolved, there’d be only a limited number of workable solutions that gave harmonious sounds. To allow for modulations from one key to another, an octave has to be divided into equal parts and the corresponding tones have to be at frequencies that bear certain mathematical ratios to one another. The compromise that’s emerged in Western music is the 12-TET scale. That scale, said von Hoerner, might crop up in the music of other worlds, as might a couple of other scales that offer good compromises for polyphony: the 5-tone scale and the 31-tone scale. The latter was written about in the seventeenth century by a number of scholars, including the astronomer Christiaan Huygens, and might be the scale of choice among beings whose auditory systems are more sensitive than our own. Aliens whose biology made them less adept at differentiating between closely spaced pitches would perhaps be more likely to use 5-TET.

It’s often assumed that the first message we receive from ‘out there’ will be scientific or mathematical in content. But what better way to extend a greeting than by sending a really good piece of music, one that has not just a logical basis but is full of the passion and emotions of its creators.