![]()
1 + 2 + 3 + 4 + ··· + 100 = 5050
The Magic of NumbersThe Magic of Numbers
Number Patterns
The study of mathematics begins with numbers. In school, after we learn how to count and represent numbers using words or digits or physical objects, we spend many years manipulating numbers through addition, subtraction, multiplication, division, and other arithmetical procedures. And yet, we often don’t get to see that numbers possess a magic of their own, capable of entertaining us, if we just look below the surface.
Let’s start with a problem given to a mathematician named Karl Friedrich Gauss when he was just a boy. Gauss’s teacher asked him and his classmates to add up all the numbers from 1 to 100, a tedious task designed to keep the students busy while the teacher did other work. Gauss astonished his teacher and classmates by immediately writing down the answer: 5050. How did he do it? Gauss imagined the numbers 1 through 100 split into two rows, with the numbers 1 through 50 on the top and the numbers 51 through 100 written backward on the bottom, as shown below. Gauss observed that each of the 50 columns would add up to the same sum, 101, and so their total would just be 50 × 101, which is 5050.
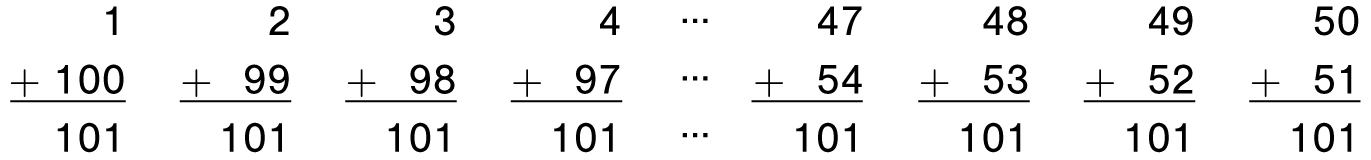
Splitting the numbers from 1 to 100 into two rows; each pair of numbers adds to 101
Gauss went on to become the greatest mathematician of the nineteenth century, not because he was quick at doing mental calculations, but because of his ability to make numbers dance. In this chapter, we will explore many interesting number patterns and start to see how numbers dance. Some of these patterns can be applied to do mental calculations more quickly, and some are just beautiful for their own sake.
We’ve used Gauss’s logic to sum the first 100 numbers, but what if we wanted to sum 17 or 1000 or 1 million? We will, in fact, use his logic to sum the first n numbers, where n can be any number you want! Some people find numbers to be less abstract when they can visualize them. We call the numbers 1, 3, 6, 10, and 15 triangular numbers, since we can create triangles like the ones below using those quantities of dots. (You might dispute that 1 dot forms a triangle, but nevertheless 1 is considered triangular.) The official definition is that the nth triangular number is 1 + 2 + 3 + · · · + n.
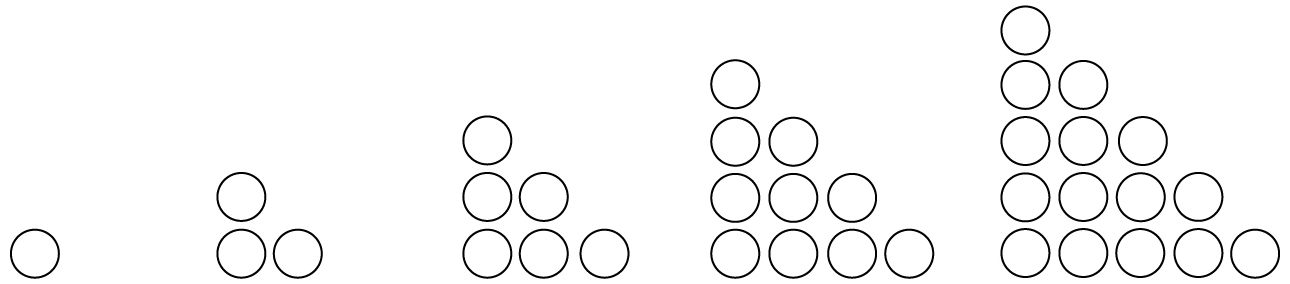
The first 5 triangular numbers are 1, 3, 6, 10, and 15
Notice what happens when we put two triangles side by side, as depicted on the opposite page:
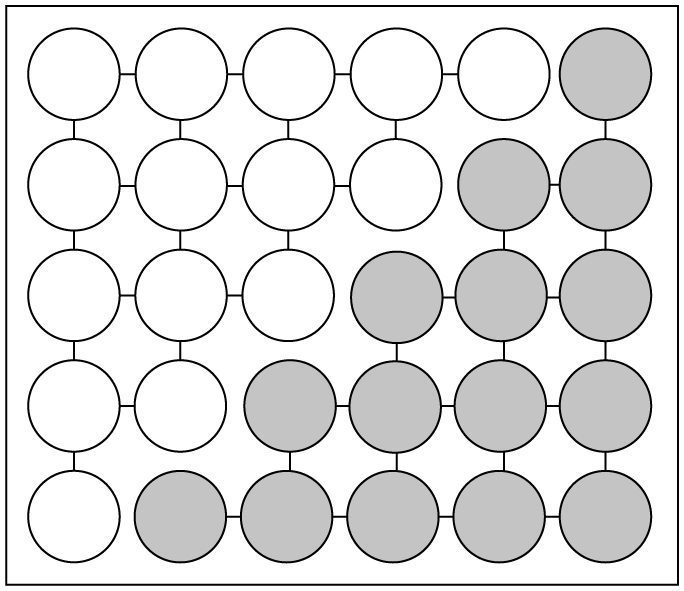

How many dots are in the rectangle?
Since the two triangles form a rectangle with 5 rows and 6 columns, there are 30 dots altogether. Hence, each original triangle must have half as many dots, namely 15. Of course, we knew that already, but the same argument shows that if you take two triangles with n rows and put them together as we did, then you form a rectangle with n rows and n + 1 columns, which has n × (n + 1) dots (often written more succinctly as n(n + 1) dots). As a result, we have derived the promised formula for the sum of the first n numbers:


Notice what we just did: we saw a pattern to sum the first 100 numbers and were able to extend it to handle any problem of the same form. If we needed to add the numbers 1 through 1 million, we could do it in just two steps: multiply 1,000,000 by 1,000,001, then divide by 2!
Once you figure out one mathematical formula, other formulas often present themselves. For example, if we double both sides of the last equation, we get a formula for the sum of the first n even numbers:
2 + 4 + 6 + ··· + 2n = n(n + 1)
What about the sum of the first n odd numbers? Let’s look at what the numbers seem to be telling us.
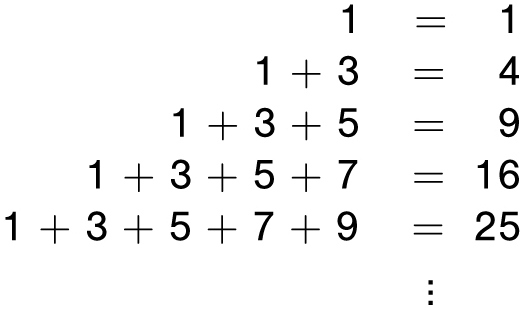
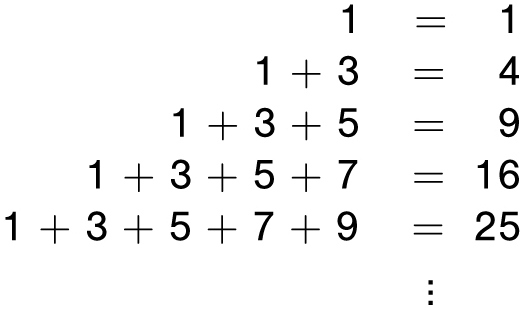
What is the sum of the first n odd numbers?
The numbers on the right are perfect squares: 1 × 1, 2 × 2, 3 × 3, and so on. It’s hard to resist noticing the pattern that the sum of the first n odd numbers seems to be n × n, often written as n2. But how can we be sure that this is not just some temporary coincidence? We’ll see a few ways to derive this formula in Chapter 6, but such a simple pattern should have a simple explanation. My favorite justification uses a count-the-dots strategy again, and reminds us of why we call numbers like 25 perfect squares. Why should the first 5 odd numbers add to 52? Just look at the picture of the 5-by-5 square below.


How many dots are in the square?
This square has 5 × 5 = 25 dots, but let’s count the dots another way. Start with the 1 dot in the upper left corner. It is surrounded by 3 dots, then 5 dots, then 7 dots, then 9 dots. Consequently,
1 + 3 + 5 + 7 + 9 = 52
If we started with an n-by-n square, then we can break it into n (backward) L-shaped regions of sizes 1, 3, 5, . . . , (2n − 1). When viewed this way, we have a formula for the sum of the first n odd numbers:
1 + 3 + 5 + ··· + (2n − 1) = n2
Aside
Later in this book, we’ll see how the approach of counting dots (and the general approach of answering a question in two different ways) leads to some interesting results in advanced mathematics. But it can also be useful for understanding elementary mathematics as well. For example, why does 3 × 5 = 5 × 3? I’m sure you haven’t even questioned that statement since you were told, as a child, that the order of multiplication doesn’t matter. (Mathematicians say that multiplication of numbers is commutative.) But why should 3 bags of 5 marbles contain the same amount as 5 bags of 3 marbles? The explanation is simple if you just count the dots in a 3-by-5 rectangle. Counting row by row, we see 3 rows of 5 dots apiece, giving us 3 × 5 dots. On the other hand, we also have 5 columns with 3 dots apiece, so there are also 5 × 3 dots.
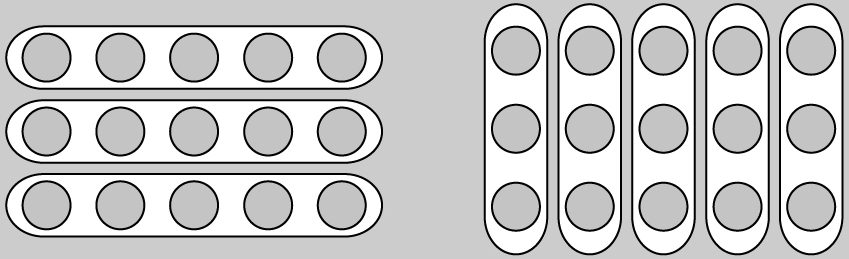
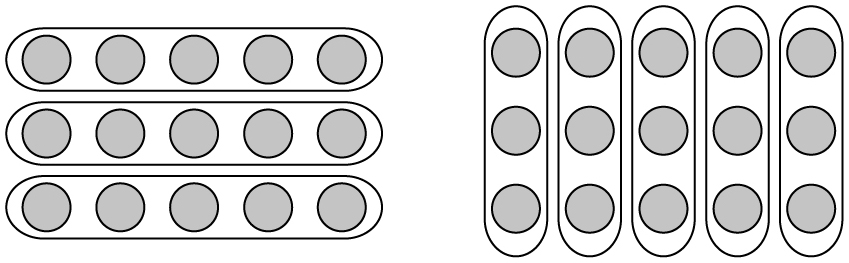
Why does 3 × 5 = 5 × 3?
Let’s apply the pattern from the sum of odd numbers to find an even more beautiful pattern. If our goal is to make the numbers dance, then you might say we are about to do some square dancing.
Consider this interesting pyramid of equations:


What patterns do you see? It’s easy to count the numbers in each row: 3, 5, 7, 9, 11, and so on. Next comes an unexpected pattern. What is the first number of each row? Judging from the first 5 rows, 1, 4, 9, 16, 25, . . . , they appear to be the perfect squares. Why is that? Let’s look at the fifth row. How many numbers appear before row 5? If we count the numbers in the preceding four rows, we have 3 + 5 + 7 + 9. To get the leading number of row 5, we just add 1 to this sum, so we really have the sum of the first 5 odd numbers, which we now know to be 52.
Now let’s verify the fifth equation without actually adding any numbers. What would Gauss do? If we temporarily ignore the 25 at the beginning of the row, then there are 5 remaining numbers on the left, which are each 5 less than their corresponding numbers on the right.
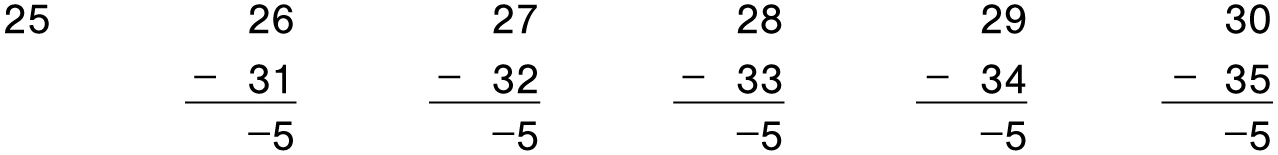
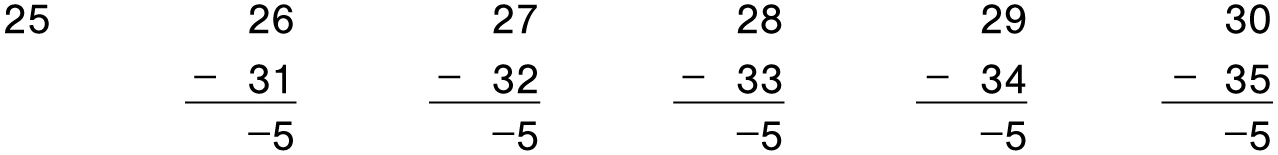
Comparing the left side of row 5 with the right side of row 5
Hence the five numbers on the right have a total that is 25 greater than their corresponding numbers on the left. But this is compensated for by the number 25 on the left. Hence the sums balance as promised. By the same logic, and a little bit of algebra, it can be shown that this pattern will continue indefinitely.
Aside
For those who wish to see the little bit of algebra now, here it is. Row n is preceded by 3 + 5 + 7 + · · · + (2n − 1) = n2 − 1 numbers, so the left side of the equation must start with the number n2, followed by the next n consecutive numbers, n2 + 1 through n2 + n. The right side has n consecutive numbers starting with n2 + n + 1 through n2 + 2n. If we temporarily ignore the n2 number on the left, we see that the n numbers on the right are each n larger than their corresponding numbers on the left, so their difference is n × n, which is n2. But this is compensated for on the left by the initial n2 term, so the equations balance.
Time for a new pattern. We saw that odd numbers could be used to make squares. Now let’s see what happens when we put all the odd numbers in one big triangle, as shown on the next page.
We see that 3 + 5 = 8, 7 + 9 + 11 = 27, 13 + 15 + 17 + 19 = 64. What do the numbers 1, 8, 27, and 64 have in common? They are perfect cubes! For example, summing the five numbers in the fifth row, we get
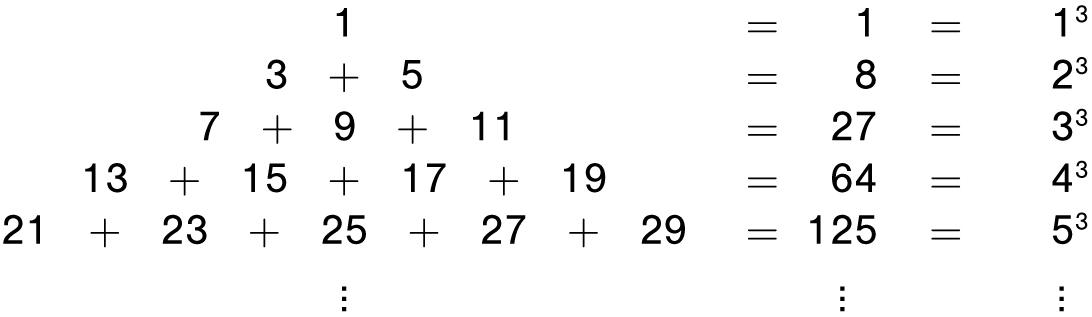
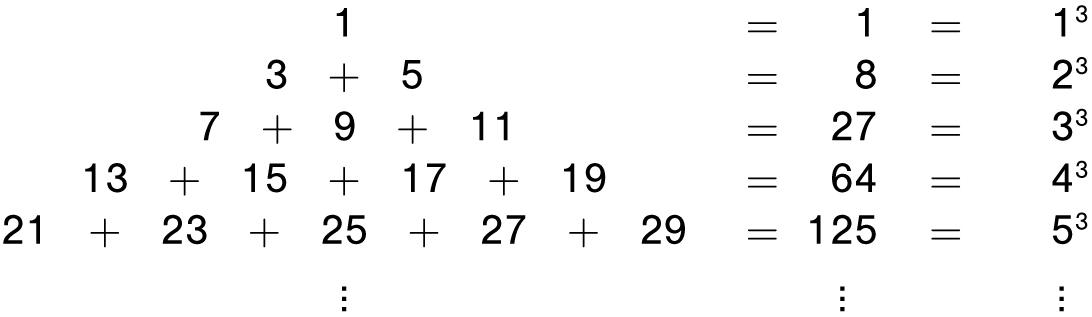
An odd triangle
21 + 23 + 25 + 27 + 29 = 125 = 5 × 5 × 5 = 53
The pattern seems to suggest that the sum of the numbers in the nth row is n3. Will this always be the case, or is it just some odd coincidence? To help us understand this pattern, check out the middle numbers in rows 1, 3, and 5. What do you see? The perfect squares 1, 9, and 25. Rows 2 and 4 don’t have middle numbers, but surrounding the middle are the numbers 3 and 5 with an average of 4, and the numbers 15 and 17 with an average of 16. Let’s see how we can exploit this pattern.
Look again at row 5. Notice that we can see that the sum is 53 without actually adding the numbers by noticing that these five numbers are symmetrically centered around the number 25. Since the average of these five numbers is 52, then their total must be 52 + 52 + 52 + 52 + 52 = 5 × 52, which is 53. Similarly, the average of the four numbers of row 4 is 42, so their total must be 43. With a little bit of algebra (which we won’t do here), you can show that the average of the n numbers in row n is n2, so their total must be n3, as desired.
Since we’re talking about cubes and squares, I can’t resist showing you one more pattern. What totals do you get as you add the cubes of numbers starting with 13?
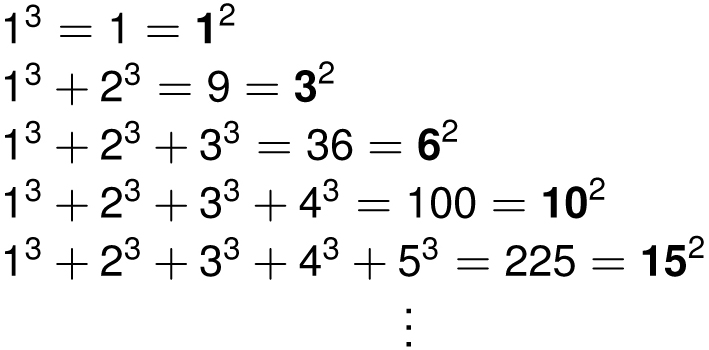
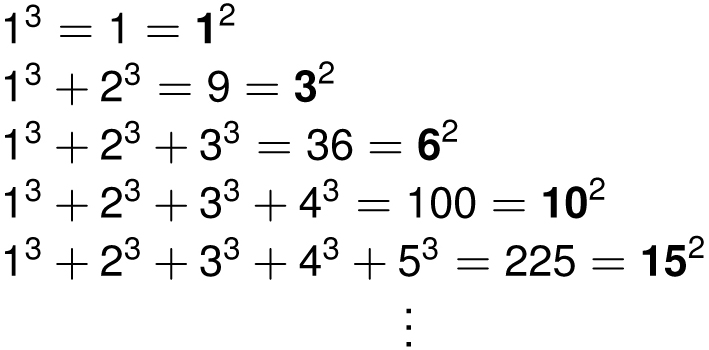
The sum of the cubes is always a perfect square
When we start summing cubes, we get the totals 1, 9, 36, 100, 225, and so on, which are all perfect squares. But they’re not just any perfect squares; they are the squares of 1, 3, 6, 10, 15, and so on, which are all triangular numbers! Earlier we saw that these were the sums of integers and so, for example,
13 + 23 + 33 + 43 + 53 = 225 = 152 = (1 + 2 + 3 + 4 + 5)2
To put it another way, the sum of the cubes of the first n numbers is the square of the sum of the first n numbers. We’re not quite ready to prove that result now, but we will see two proofs of this in Chapter 6.
Fast Mental Calculations
Some people look at these number patterns and say, “Okay, that’s nice. But what good are they?” Most mathematicians would probably respond like any artist would—by saying that a beautiful pattern needs no justification other than its beauty. And the patterns become even more beautiful the more deeply we understand them. But sometimes the patterns can lead to real applications.
Here’s a simple pattern that I had the pleasure of discovering (even if I wasn’t the first person to do so) when I was young. I was looking at pairs of numbers that added up to 20 (such as 10 and 10, or 9 and 11), and I wondered how large the product could get. It seemed that the largest product would occur when both numbers were equal to 10, and the pattern confirmed that.


The product of numbers that add to 20
The pattern was unmistakable. As the numbers were pulled farther apart, the product became smaller. And how far below 100 were they? 1, 4, 9, 16, 25, . . . , which were 12, 22, 32, 42, 52, and so on. Does this pattern always work? I decided to try another example, by looking at pairs of numbers that add up to 26.


The product of numbers that add to 26
Once again, the product was maximized when we chose the two numbers to be equal, and then the product decreased from 169 by 1, then 4, then 9, and so on. After a few more examples, I was convinced that the pattern was true. (I’ll show you the algebra behind it later.) Then I saw a way that this pattern could be applied to squaring numbers faster.
Suppose we want to square the number 13. Instead of performing 13 × 13 directly, we will perform the easier calculation of 10 × 16 = 160. This is almost the answer, but since we went up and down 3, it is shy of the answer by 32. Thus,
132 = (10 × 16) + 32 = 160 + 9 = 169
Let’s try another example. Try doing 98 × 98 using this method. To do this, we go up 2 to 100, then down 2 to 96, then add 22. That is,
982 = (100 × 96) + 22 = 9600 + 4 = 9604
Squaring numbers that end in 5 are especially easy, since when you go up and down 5, the numbers you are multiplying will both end in 0. For example,
352 = (30 × 40) + 52 = 1200 + 25 = 1225
552 = (50 × 60) + 52 = 3000 + 25 = 3025
852 = (80 × 90) + 52 = 7200 + 25 = 7225
Now try 592. By going up and down 1, you get 592 = (60 × 58) + 12 But how should you mentally calculate 60 × 58? Three words of advice: left to right. Let’s first ignore the 0 and compute 6 × 58 from left to right. Now 6 × 50 = 300 and 6 × 8 = 48. Add those numbers together (from left to right) to get 348. Therefore, 60 × 58 = 3480, and so
592 = (60 × 58) + 12 = 3480 + 1 = 3481
Aside
Here’s the algebra that explains why this method works. (You may want to come back to this after reading about the difference of squares in Chapter 2.)
A2 = (A + d)(A − d) + d2
where A is the number being squared, and d is the distance to the nearest easy number (although the formula works for any number d). For example, when squaring 59, A = 59 and d = 1, so the formula tells you to do (59 + 1) × (59 − 1) + 12, as in the previous calculation.
Once you get good at squaring two-digit numbers, you can square three-digit numbers by the same method. For example, if you know that 122 = 144, then
1122 = (100 × 124) + 122 = 12,400 + 144 = 12,544
A similar method can be used for multiplying any two numbers that are close to 100. When you first see the method, it looks like pure magic. Look at the problem 104 × 109. Next to each number we write down its distance from 100, as in the figure below. Now add the first number to the second distance number. Here, that would be 104 + 9 = 113. Then multiply the distance numbers together. In this case, 4 × 9 = 36. Push those numbers together and your answer magically appears.
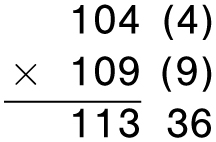
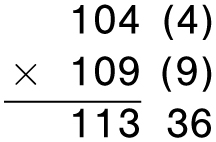
A magical way to multiply numbers close to 100—here, 104 × 109 = 11,336
I’ll show you more examples of this and the algebra behind it in Chapter 2. But while we’re on the subject, let me say a few more words about mental math. We spend an awful amount of time learning pencil-and-paper arithmetic, but precious little time learning how to do math in your head. And yet, in most practical situations, you are more likely to need to calculate mentally than to calculate on paper. For most large calculations, you will use a calculator to get the exact answer, but you generally don’t use a calculator when reading a nutrition label or hearing a speech or listening to a sales report. For those situations, you typically just want a good mental estimate of the important quantities. The methods taught in school are fine for doing math on paper, but they are generally poor for doing math in your head.
I could write a book on fast mental math strategies, but here are some of the essential ideas. The main tip, which I cannot emphasize enough, is to do the problems from left to right. Mental math is a process of constant simplification. You start with a hard problem and simplify it to easier problems until you reach your answer at the end.
Mental addition.
Consider a problem like
314 + 159
(I’m writing the numbers horizontally so you’re less tempted to go into pencil-and-paper mode.) Starting with 314, first add the number 100 to give us a simpler addition problem:
414 + 59
Adding 50 to 414 gives us an even simpler problem that we can solve right away:
464 + 9 = 473
That is the essence of mental addition. The only other occasionally useful strategy is that sometimes we can turn a hard addition problem into an easy subtraction problem. This often arises if we are adding the price of retail items. For example, let’s do
$23.58 + $8.95
Since $8.95 is 5 cents below $9, we first add $9 to $23.58, then subtract 5 cents. The problem simplifies to
$32.58 − $0.05 = $32.53
Mental subtraction.
The most important idea with mental subtraction problems is the strategy of oversubtracting. For example, when subtracting 9, it’s often easier to first subtract 10, then add back 1. For example,
83 − 9 = 73 + 1 = 74
Or to subtract 39, it’s probably easier to first subtract 40, then add back 1.
83 − 39 = 43 + 1 = 44
When subtracting numbers with two or more digits, the key idea is to use complements. (You’ll compliment me later for this.) The complement of a number is its distance to the next-highest round number. With one-digit numbers, this is the distance to 10. (For example, the complement of 9 is 1.) For two-digit numbers, this is the distance to 100. Look at the following pairs of numbers that add to 100. What do you notice?
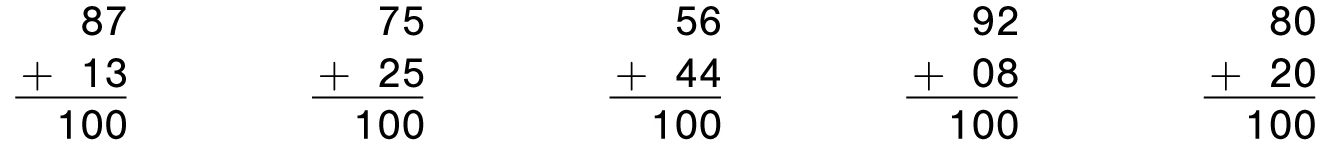
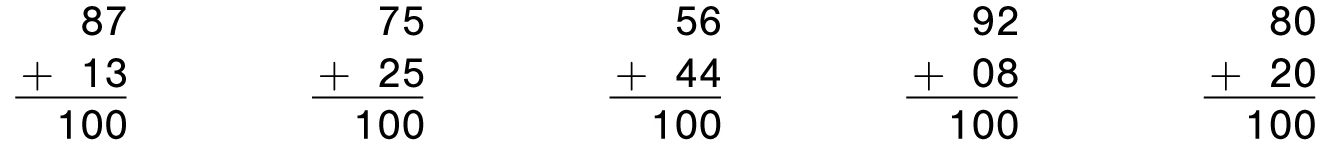
Complementary two-digit numbers sum to 100
We say that the complement of 87 is 13, the complement of 75 is 25, and so on. Conversely, the complement of 13 is 87 and the complement of 25 is 75. Reading each problem from left to right, you will notice that (except for the last problem) the leftmost digits add to 9 and the rightmost digits add to 10. The exception is when the numbers end in 0 (as in the last problem). For example, the complement of 80 is 20.
Let’s apply the strategy of complements for the problem 1234 − 567. Now, that would not be a fun problem to do on paper. But with complements, hard subtraction problems become easy addition problems! To subtract 567, we begin by subtracting 600. That’s easy to do, especially if you think from left to right: 1234 − 600 = 634. But you’ve subtracted too much. How much too much? Well, how far is 567 from 600? It’s the same as the distance between 67 and 100, which is 33. Thus
1234 − 567 = 634 + 33 = 667
Notice that the addition problem is especially easy because there are no “carries” involved. This will often be the case when doing subtraction problems by complements:
Something similar happens with three-digit complements.
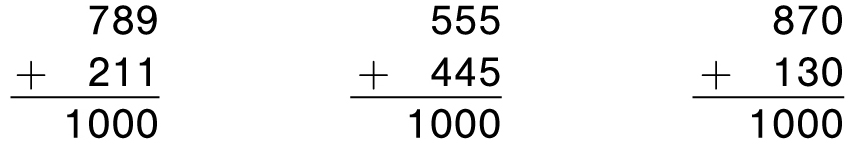
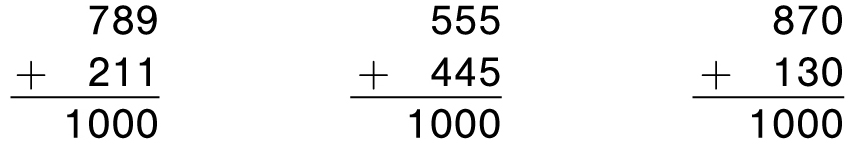
Complementary three-digit numbers sum to 1000
For most problems (when the number does not end in zero), the corresponding digits sum to 9, except the last pair of digits sum to 10. For example, with 789, 7 + 2 = 9, 8 + 1 = 9, and 9 + 1 = 10. This can be handy when making change. For example, my favorite sandwich from my local deli costs $6.76. How much change would I get from $10.00? The answer is found by taking the complement of 676, which is 324. Hence the change back is $3.24.
Aside
Whenever I buy this sandwich, I can’t help but notice that both the price and the change were perfect squares (262 = 676 and 182 = 324). (Bonus question: There is another pair of perfect squares that add up to 1000. Can you find them?)
Mental multiplication.
After you have memorized your multiplication table through 10, you can mentally calculate, at least approximately, the answer to any multiplication problem. The next step is to master (but not memorize!) your one-digit times two-digit multiplication problems. The key idea is to work from left to right. For example, when multiplying 8 × 24, you should first multiply 8 × 20, then add this to 8 × 4:
8 × 24 = (8 × 20) + (8 × 4) = 160 + 32 = 192
Once you’ve mastered those, it’s time to practice one-digit times three-digit multiplication problems. These are a bit trickier, since there is more to keep in your memory. The key here is to gradually add the numbers as you go along so there is not as much to remember. For example, when multiplying 456 × 7, you stop to add 2800 + 350, as below, before adding 42 to it.
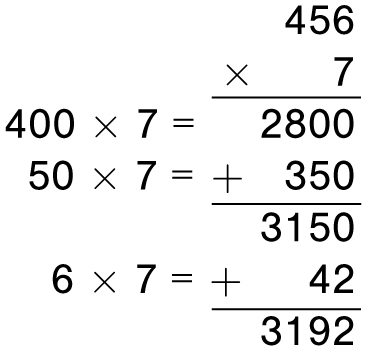
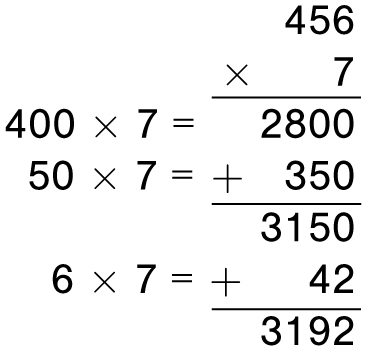
Once you have the hang of doing problems of this size, then it’s time to move on to two-digit times two-digit problems. For me, this is where the fun begins, because there are usually many different ways you can attack these problems. By doing the problem multiple ways, you can check your answer—and simultaneously revel in the consistency of arithmetic! I’ll illustrate all of these methods with a single example, 32 × 38.
The most familiar method (most closely resembling what you do on paper) is the addition method, which can be applied to any problem. Here we break up one number (usually the one with the smaller ones digit) into two parts, then multiply each part by the other number, and add the results together. For example,
32 × 38 = (30 + 2) × 38 = (30 × 38) + (2 × 38) = ···
Now how do we calculate 30 × 38? Let’s do 3 × 38, then attach the 0 at the end. Now 3 × 38 = 90 + 24 = 114, so 30 × 38 = 1140. Then 2 × 38 = 60 + 16 = 76, so
32 × 38 = (30 × 38) + (2 × 38) = 1140 + 76 = 1216
Another way to do a problem like this (typically when one of the numbers ends in 7, 8, or 9) is to use the subtraction method. Here we exploit the fact that 38 = 40 − 2 to get
38 × 32 = (40 × 32) − (2 × 32) = 1280 − 64 = 1216
The challenge with the addition and subtraction methods is that they require you to hold on to a big number (like 1140 or 1280) while doing a separate calculation. That can be difficult. My usual preferred method for two-digit multiplication is the factoring method, which can be applied whenever one of the numbers can be expressed as the product of two 1-digit numbers. In our example, we see that 32 can be factored as 8 × 4. Consequently,
38 × 32 = 38 × 8 × 4 = 304 × 4 = 1216
If we factor 32 as 4 × 8, we get 38 × 4 × 8 = 152 × 8 = 1216, but I prefer to multiply the two-digit number by the larger factor first, so that the next number (usually a three-digit number) is multiplied by the smaller factor.
Aside
The factoring method also works well on multiples of 11, since there is an especially easy trick for multiplying by 11: just add the digits and put the total in between. For example, to do 53 × 11, we see that 5 + 3 = 8, so the answer is 583. What’s 27 × 11? Since 2 + 7 = 9, the answer is 297. What if the total of the two digits is bigger than 9? In that case, we insert the last digit of the total and increase the first digit by 1. For example, to compute 48 × 11, since 4 + 8 = 12, the answer is 528. Similarly, 74 × 11 = 814. This can be exploited when multiplying numbers by multiples of 11. For example,
74 × 33 = 74 × 11 × 3 = 814 × 3 = 2442
Another fun method for multiplying two-digit numbers is the close together method. You can use it when both numbers begin with the same digit. It seems utterly magical when you first watch it in action. For example, would you believe that
38 × 32 = (30 × 40) + (8 × 2) = 1200 + 16 = 1216
The calculation is especially simple (as in the example above) when the second digits sum to 10. (Here, both numbers begin with 3 and the second digits have the sum 8 + 2 = 10.) Here’s another example:
83 × 87 = (80 × 90) + (3 × 7) = 7200 + 21 = 7221
Even when the second digits don’t add up to 10, the calculation is almost as simple. For example, to multiply 41 × 44, if you decrease the smaller number by 1 (to reach the round number 40), then you must increase the larger number by 1 as well. Consequently,
41 × 44 = (40 × 45) + (1 × 4) = 1800 + 4 = 1804
For 34 × 37, if you decrease 34 by 4 (to reach the round number 30), then it gets multiplied by 37 + 4 = 41, and then we add 4 × 7 as follows:
34 × 37 = (30 × 41) + (4 × 7) = 1230 + 28 = 1258
By the way, the mysterious multiplication we saw earlier of 104 × 109 was just an application of this same method.
104 × 109 = (100 × 113) + (04 × 09) = 11300 + 36 = 11,336
Some schools are asking students to memorize their multiplication tables through 20. Rather than memorize these products, we can calculate them quickly enough using this method. For example,
17 × 18 = (10 × 25) + (7 × 8) = 250 + 56 = 306
Why does this mysterious method work? For this, we’ll need algebra, which we will discuss in Chapter 2. And once we have algebra, we can find new ways to calculate. For example, we’ll see why the last problem can also be done as follows:
18 × 17 = (20 × 15) + ((−2) × (−3)) = 300 + 6 = 306
Speaking of the multiplication table, check out the one-digit table on the opposite page that I promised earlier. Here’s a question that would appeal to a young Gauss: What is the sum of all the numbers in the multiplication table? Take a minute and see if you can figure it out in an elegant way. I’ll provide the answer at the end of the chapter.
Mental estimation and division.
Let’s begin with a very simple question with a very simple answer that we are rarely taught in school:
(a) If you multiply two 3-digit numbers together, can you immediately tell how many digits can be in the answer?
And a follow-up question:
(b) How many digits can be in the answer when multiplying a four-digit number by a five-digit number?
We spend so much time in school learning to generate the digits of a multiplication or division problem, and very little time thinking about the important aspects of the answer. Yet it’s way more important to know the approximate size of the answer than to know the last digits or even the first digits. (Knowing that the answer begins with 3 is meaningless until you know whether the answer will be closer to 30,000 or 300,000 or 3,000,000.) The answer to question (a) is five or six digits. Why is that? The smallest possible answer is 100 × 100 = 10,000, which has five digits. The biggest possible answer is 999 × 999, which is strictly less than 1000 × 1000 = 1,000,000, which has seven digits (but just barely!). Since 999 × 999 is smaller, then it must have six digits. (Of course, you could easily compute the last answer in your head: 9992 = (1000 × 998) + 12 = 998,001.) Hence the product of two 3-digit numbers must have five or six digits.
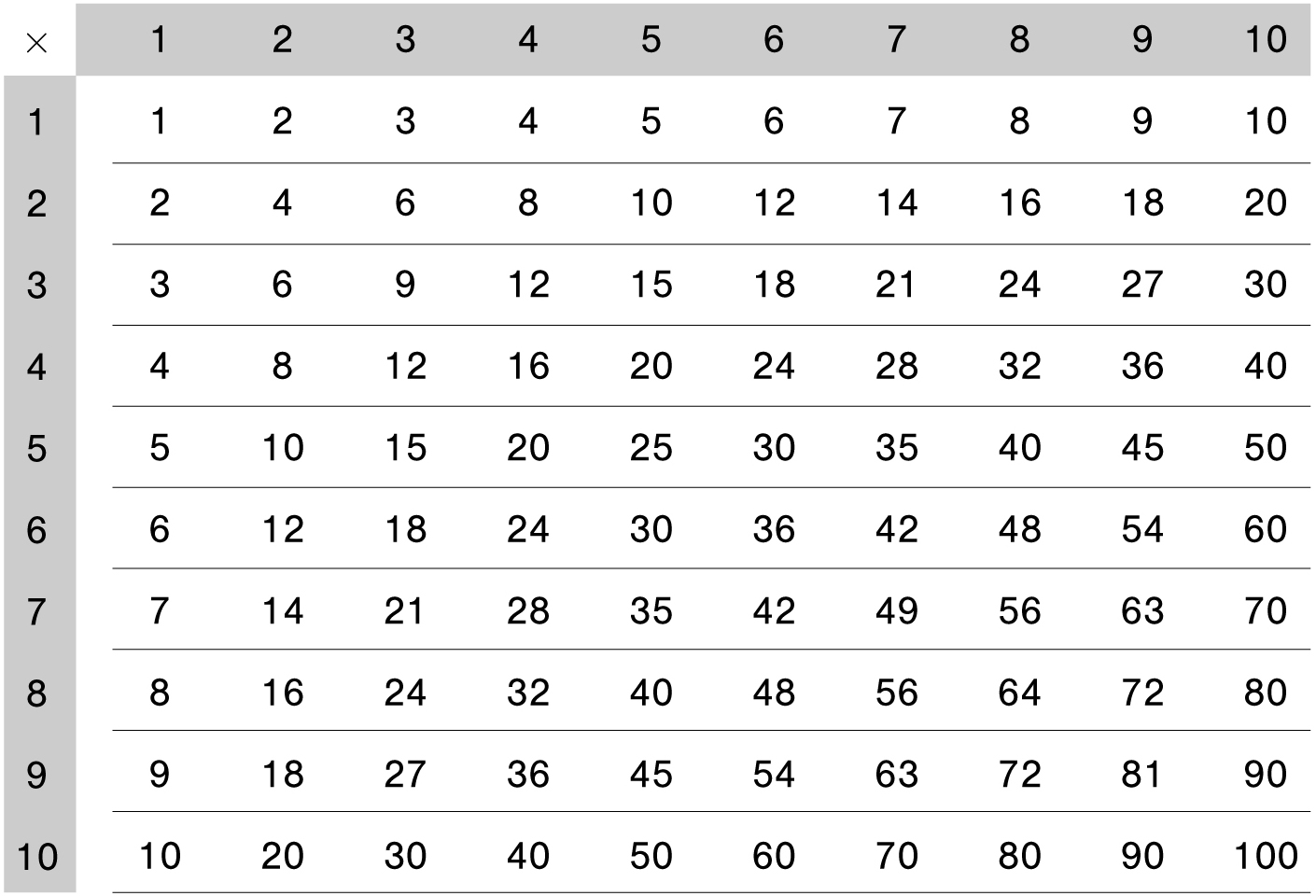

What is the sum of all 100 numbers in the multiplication table?
The answer to question (b) is eight or nine digits. Why? The smallest four-digit number is 1000, also known as 103 (a 1 followed by three zeros). The smallest five-digit number is 10,000 = 104. So the smallest product is 103 × 104 = 107, which has eight digits. (Where does 107 comes from? 103 × 104 = (10 × 10 × 10) × (10 × 10 × 10 × 10) = 107.) And the largest product will be just a hair less than the ten-digit number 104 × 105 = 109, so the answer has at most nine digits.
By applying this logic, we arrive at a simple rule: An m-digit number times an n-digit number has m + n or m + n − 1 digits.
It’s usually easy to determine how many digits will be in the answer just by looking at the leading (leftmost) digits of each number. If the product of the leading digits is 10 or larger, then the product is guaranteed to have m + n digits. (For example, with 271 × 828, the product of the leading digits is 2 × 8 = 16, so the answer has six digits.) If the product of the leading digits is 4 or smaller, then it will have m + n − 1 digits. For example, 314 × 159 has five digits. If the product of the leading digits is 5, 6, 7, 8, or 9, then closer inspection is required. For example, 222 × 444 has five digits, but 234 × 456 has six digits. Both answers are very close to 100,000, which is really what matters.)
By reversing this rule, we get an even simpler rule for division: An m-digit number divided by an n-digit number has m − n or m − n + 1 digits.
For example, a nine-digit number divided by a five-digit number must have four or five digits. The rule for determining which answer to choose is even easier than the multiplication situation. Instead of multiplying or dividing the leading digits, we simply compare them. If the leading digit of the first number (the number being divided) is smaller than the leading digit of the second number, then it’s the smaller choice (m − n). If the leading digit of the first number is larger than the leading digit of the second number, then it’s the larger choice (m − n + 1). If the leading digits are the same, then we look at the second digits and apply the same rule. For instance 314,159,265 divided by 12,358 will have a five-digit answer, but if we instead divide it by 62,831, the answer will have four digits. Dividing 161,803,398 by 14,142 will result in a five-digit answer since 16 is greater than 14.
I won’t go through the process of doing mental division since it is similar to the pencil-and-paper method. (Indeed, any method for division problems on paper requires you to generate the answer from left to right!) But here are some shortcuts that can sometimes be handy.
When dividing by 5 (or any number ending in 5), the problem usually simplifies if you double the numerator and denominator. For example:
34 ÷ 5 = 68 ÷ 10 = 6.8
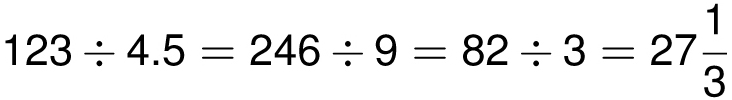
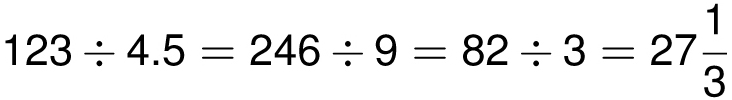
After doubling both numbers, you might notice that both 246 and 9 are divisible by 3 (we’ll say more about this in Chapter 3), so we can simplify the division problem further by dividing both numbers by 3.
Aside
Look at the reciprocals of all the numbers from 1 to 10:
1/2 = 0.5, 1/3 = 0.333 . . . , 1/4 = 0.25, 1/5 = 0.2
1/6 = 0.1666 . . . , 1/8 = 0.125, 1/9 = 0.111 . . . , 1/10 = 0.1
All of the decimal expansions above either terminate or repeat after two terms. But the one weird exception is the fraction for 1/7, which repeats after six decimal places:
1/7 = 0.142857 142857 . . .
(The reason all the other reciprocals end so quickly is that the other numbers from 2 through 11 divide into either 10, 100, 1000, 9, 90, or 99, but the first nice number that 7 divides into is 999,999.) If you write the decimal digits of 1/7 in a circle, something magical happens:
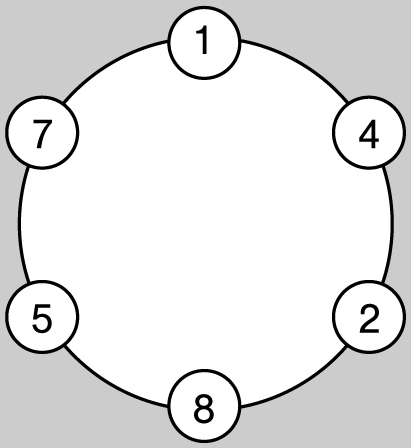
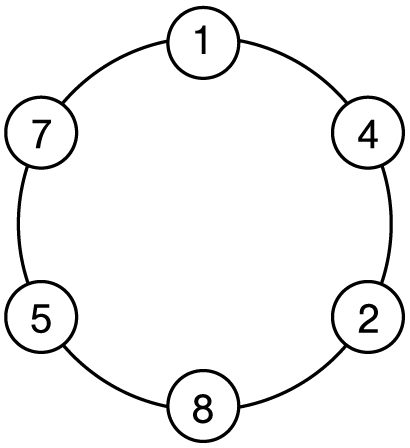
The 7th circle
What’s remarkable is that all the other fractions with denominator 1/7 can also be created by going around the circle forever from the appropriate starting point. Specifically,
1/7 = 0.142857 142857 . . . , 2/7 = 0.285714 285714 . . . ,
3/7 = 0.428571 428571 . . . , 4/7 = 0.571428 571428 . . . ,
5/7 = 0.714285 714285 . . . , 6/7 = 0.857142 857142 . . .
Let’s end this chapter with the question we asked a few pages ago. What is the sum of all the numbers in the multiplication table? When you first read the question, it seems intimidating, just as summing the first 100 numbers might have. By becoming more familiar with the beautiful patterns that emerge when numbers dance, we have a better chance of finding a beautiful answer to this question.
We begin by adding the numbers in the first row. As Gauss (or our triangular number formula or just simple addition) could tell us:
1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 = 55
What about the sum of the second row? Well, that’s just
2 + 4 + 6 + ··· + 20 = 2(1 + 2 + 3 + ··· + 10) = 2 × 55
By the same reasoning, the third row will sum to 3 × 55. Continuing this logic, we conclude that the sum of all of these numbers is
(1 + 2 + 3 + ··· + 10) × 55 = 55 × 55 = 552
which you should now be able to do in your head . . . 3025!