In the mid-nineteenth century, while Maxwell was using mathematics to discover that light was an electromagnetic wave, other scientists were exploring the atomic nature of matter. Though the existence of atoms was still a hypothesis, evidence was mounting that matter really was made up of tiny individual particles in constant motion. No other theory could better explain the way substances reacted chemically and the way gases behaved when heated or put under pressure.
Maxwell also contributed to atomic theory through his work in the mathematics behind the laws of thermodynamics, the branch of physics dealing with heat and temperature. He and others found that the best way to understand heat was by considering it the internal energy of matter due to the rapid motion of atoms.

Max Planck (1858–1947). In 1900, to explain the shape of the spectrum produced by hot bodies, Planck developed a theory that described light as being emitted in packets of energy called quanta rather than as a continuous stream. Though he considered it only a mathematical trick, it soon became apparent that quanta were real. Today we know them as photons.
A Puzzle in the Glow
One of the questions those scientists wondered about was the glow produced when an object is heated. How do hot objects transform their heat energy—the motion of their atoms—into light, that is, electromagnetic waves? Could they explain how, as its temperature rises, a heated body’s glow becomes brighter and its color changes from deep red, to brighter red, to orange and yellow?
In 1895, the renowned Professor Max Planck (1858–1947) at the University of Berlin in Germany turned his theoretical skills to that question. Could he come up with a formula that described the spectrum—the mixture of different colors of light—that radiates from hot bodies? Using a spectrometer, a device that spreads light into its component colors like a prism, scientists had observed the light that came from holes cut into the sides of very hot furnaces. Planck looked at the graphs of their experimental data, showing how the brightness varied for each color in the glow, and tried to find a formula that would match the curves he saw there in every detail.
To represent a color mathematically, Planck used its corresponding frequency (how fast the electromagnetic wave wiggles), increasing for visible light from the lowest frequency at the red end of the spectrum to the highest frequency at the violet end. He even used measurements of invisible light in the infrared (below red) and ultraviolet (above violet) regions.
Planck looked at graphs for different temperatures, and noted that all had one important common feature. Starting from infrared and going toward ultraviolet, they would rise to a peak and then fall toward zero. As temperatures rose, the light was more intense, and the peaks of the graphs were higher. The peak also shifted toward higher frequencies, corresponding to the changing color of the furnaces from deep red to bright red to orange to yellow. But no matter how hot the furnaces got, the measured intensity always dropped off sharply beyond the peak.
Planck thought about what kind of a model he could use to represent a hot, radiating body. It had to lead to a formula he could use to make a prediction about its spectrum. He settled on modeling the furnace as a collection of vibrating atoms, each producing electromagnetic waves according to Maxwell’s formulas. He added those waves together to produce a spectrum and graphed it. His calculations yielded a remarkable match to actual data at the low-frequency end. But in the ultraviolet region, instead of dropping off after reaching a peak, the formula predicted an ever-rising intensity of light.
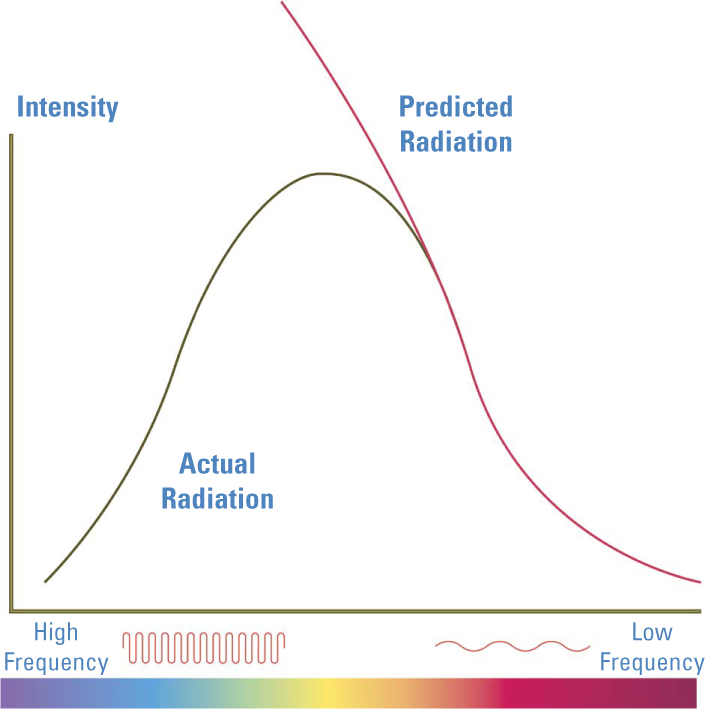
Planck’s Quanta Save the Day. As this diagram shows, the predicted spectrum of a hot body without using quanta was very accurate for long wavelengths but failed miserably for shorter wavelengths at the violet end of the spectrum. Planck’s addition of quanta produced a match at all wavelengths, eliminating what was called “the ultraviolet catastrophe.”
Planck struggled to find a fix for the problem, and finally came up with what he considered a mathematical trick. What if energy was not like a fluid that could be measured out in any amount but instead came in discrete chunks (called quanta) like grains of sand? Each atom could vibrate with zero, one, two, or three quanta of energy, and so forth; but nothing was allowed in between the whole numbers, such as a third of a quantum, two and one-half quanta, or 17.76 quanta.
Nature’s Fundamental Constants
When Planck was searching for a way to explain the shape of the spectrum of a hot body, he never suspected that he was on the trail of one of Nature’s fundamental constants. Neither did he expect to transform the way physicists understood the nature of matter and energy. But we now know that matter and energy can be viewed as both wavelike and particle-like at the same time, and the mathematical relationship between the two views contains Planck’s constant.
Planck’s constant turned out to be fundamental to understanding the nature of matter, energy, and the subatomic world. And it is not the only fundamental constant of nature. Other fundamental constants include a constant in the equation that describes the attractive force of gravity between two masses. That constant was first determined in a delicate laboratory experiment in 1798 by Henry Cavendish (1731–1810). Once people knew that value, they could use it to compute Earth’s mass by the gravitational pull at its surface.
Likewise, two fundamental constants appear in Maxwell’s equations, one describing the electrical nature and the other representing the magnetic nature of matter. When scientists realized that Maxwell’s equations combined to describe electromagnetic waves, they found that the speed of those waves was a simple mathematical combination of those two constants. That speed turned out to be another of nature’s fundamental values: the speed of light.
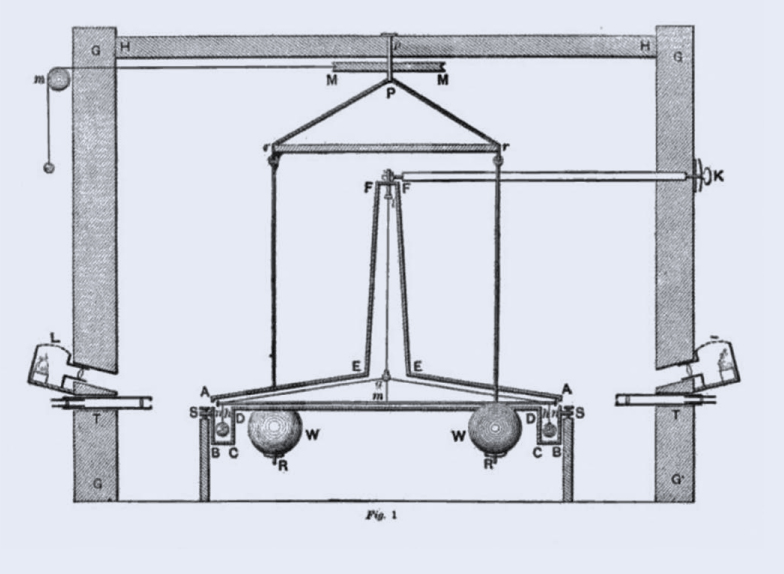
A Fundamental Discovery. When Planck proposed the light quantum, his formula included a quantity that was the ratio between the quantum’s energy and the frequency of the light. We now call that Planck’s Constant. He never imagined that the quantity was a fundamental constant of nature, just like the speed of light or the constant relating force to masses in Newton’s law of gravity. Henry Cavendish determined the Gravitational Constant using the very delicate apparatus shown here to measure the force between the large balls and the small ones nearby.
Planck realized that he needed small quanta at low frequencies, where his formulas agreed very well with measured spectra. Small quanta wouldn’t change the results, he reasoned, since you can measure out almost any volume of very fine sand. But at high frequencies, large quanta—more like a pile of pebbles than grains of sand—would limit the possible vibrations and perhaps explain the falloff in light intensity at high frequencies.
Planck began with the simplest approach. He calculated the spectrum presuming a constant ratio between the quantum’s energy and its frequency. Doubling the frequency would double the quantum’s energy. Multiplying the frequency by three would triple the energy of the quantum, and so forth.
For each temperature, Planck adjusted the ratio between the energy and the frequency of the quantum to match the calculated peak intensity to the observed peak of the spectrum. He hoped by matching the highest point on each graph that the rest of the curve would also match fairly well, but the results astonished him. The peak intensity matched, as did the shape of the entire graph, all the way from infrared to ultraviolet. Even more surprising, the same ratio that made the curve fit for one temperature also worked for all the others.
Planck published the news of that amazing ratio, which today physicists call Planck’s constant, in 1900. What began as a mathematical trick produced one of nature’s fundamental values. But what did it mean? He and other physicists were determined to find out.
Naming the Photon
Although this book is about a bundle of electromagnetic energy we call the photon, scientists did not refer to it by that name for more than two decades after it was discovered. Neither Max Planck, who invented it as a mathematical convenience in 1900, nor Albert Einstein, who first recognized it as an actual particle in 1905, used that term. They both called it a quantum or the light quantum (Lichtquant in German).
In the two decades that followed, scientists came to realize that the term quantum had much broader significance. By the 1920s, protons and electrons were well known as subatomic particles. The neutron, though not yet discovered, was also thought to exist. But the word photon had never appeared until noted American physical chemist Gilbert N. Lewis (1875–1946) proposed it in a December 1926 letter to the editor of Nature, a leading scientific journal. The word quickly found favor in the scientific community.

Gilbert N. Lewis (1875–1946). Physicists did not use the term photon to describe the light quantum until Lewis proposed it in a letter to the editor of Nature in 1926.
Quanta and the Photoelectric Effect
The explanation came from an unexpected direction, a puzzling phenomenon known as the photoelectric effect. While Planck was pondering quanta, another German physicist named Philipp Lenard (1862—1947) had discovered that shining light on a metal could cause an electric current to flow—but only under the right conditions.
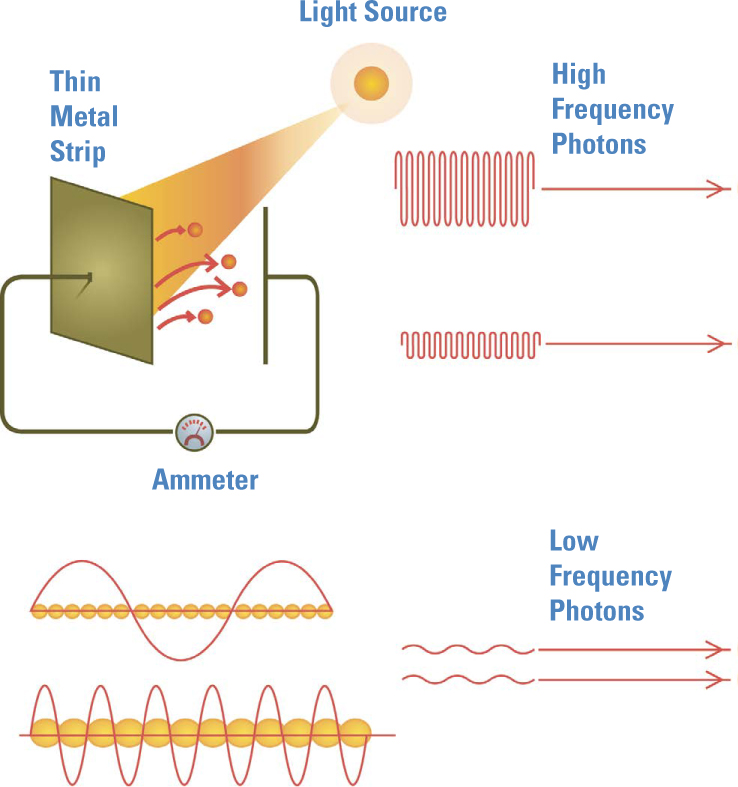
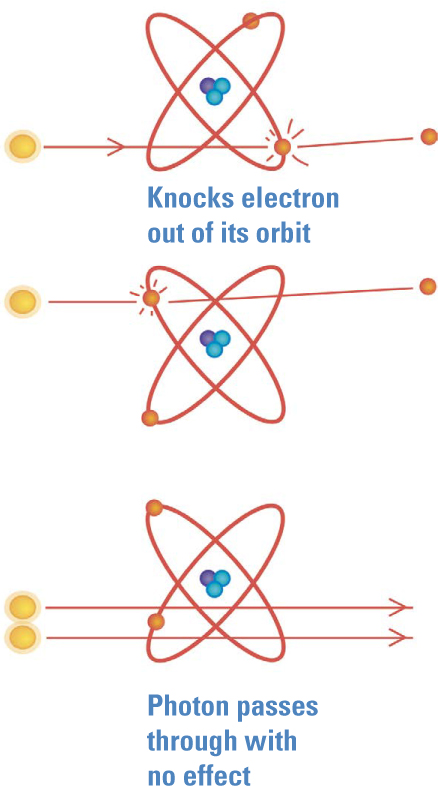
The Photoelectric Effect. At around the time Planck was proposing the quantum, Phillipp Lenard found another surprise called the photoelectric effect. Light shining on metal can, under certain circumstances, knock electrons out of a metal and create a current. The brightness of the light didn’t matter, but its color did. Above a certain threshold frequency, no matter how dim the light, a current flowed. Below that threshold, even the brightest light produced no current.

Albert Einstein recognized that the threshold corresponded to the frequency at which a single quantum had enough energy to free the electron.
The current was a stream of electrons, themselves newly discovered in 1897 and the only subatomic particles known at the time of Lenard’s research. Each metal had a particular “threshold” frequency for the light. At colors more toward the red end of the spectrum, that is, those having a frequency below the threshold, the metal did not release its electrons, no matter how intense the light. At higher frequencies, even the dimmest light would free some electrons. For most metals, that threshold was in the violet or ultraviolet range. But why should there be a threshold frequency at all?
In 1905, a little-known patent clerk in Switzerland named Albert Einstein (1879—1955) figured it out. Einstein knew that the minimum amount of energy needed to free an electron—the photoelectric threshold—varied from one metal to another. The threshold reminded him of a different phenomenon requiring a minimum amount of energy: Planck’s quantum and the radiation of hot bodies. Einstein realized that if quanta were not merely mathematical conveniences but real packets of light energy, they could explain the photoelectric threshold. These energetic bundles, which later came to be called photons (see “Naming the Photon” on page 23), would not join together like a group of people to lift a heavy load. Rather, Einstein explained, a photon either has enough energy to knock out an electron all by itself, or the electron stays put.
Below the threshold frequency, no matter how many photons are in the beam—that is, no matter how intense the light—each photon simply lacks the energy needed to knock an electron free from the metal. Above that threshold, even a single photon has enough energy to free an electron, so even the dimmest light of that color can free electrons.
The Compton Effect
Einstein’s explanation of the photoelectric effect quickly gained acceptance among physicists. Still, the photon’s nature as a particle carrying both energy and momentum had not been observed in other ways. In a Nobel Prizewinning experiment, Arthur Holly Compton (1892–1962), observed what happened when X-rays struck a graphite target. (Graphite is a form of carbon.)
Compton noted that some X-ray photons had been “scattered.” That is, they emerged at an angle away from the beam’s original direction. He assumed that the scattering was due a collision with an electron. Knowing the mass of an electron and how much energy it took to remove an electron from graphite, and then using the laws of physics for collisions, he was able to compute how the energy of the outgoing photon ought to be related to the scattering angle.
His measurements agreed precisely with his calculation, showing that the photon’s energy and momentum were related exactly as predicted by Einstein’s formulas.

Arthur Holly Compton (1892–1962). Compton was the first physicist to measure the photon’s particle properties directly. His observation of the way X-ray photons lost energy and momentum when they scattered off electrons is known as the Compton Effect.
By claiming that photons were real, however, Einstein opened up an even bigger question—or perhaps it is better to say that he reopened and transformed a question that scientists had considered closed for more than a century. Because of Young’s experiment, everyone was certain that light was made up of smooth and steady waves, not a lumpy stream of particles.
Sixty years later, Maxwell’s equations made the answer even more certain. Light waves were traveling electromagnetic energy. Planck’s mathematical trick and Einstein’s explanation of the photoelectric effect did not merely reopen the light vs. particle controversy, but they changed the form of the question from “either-or.” Light was not either a wave or a stream of photons. Somehow, it was both at once.
In the decades that followed, that surprising experimental fact led to a new scientific understanding of the nature of matter and energy, and waves and particles.