THE ADVANCE OF CELESTIAL MECHANICS
The telescope, combined with Newtonian mechanics, made it possible for humanity to glimpse a universe never before imagined and to describe what they saw with mathematical precision. Kepler's laws of planetary motion, which Newton derived from his laws of mechanics and gravity, provided a huge improvement over previous attempts to describe planetary motion. But they still were not perfect. They treated each planet as interacting gravitationally solely with the sun, neglecting the planet's interactions with other planets or with any other bodies, such as comets, asteroids, and moons.
Fortunately, this is a good approximation for our solar system because, as we saw in the last chapter, the gravitational force between two bodies is proportional to the product of their masses, and the masses of planets are very much less than the mass of the sun. Furthermore, the force falls off as 1/r2, and the planets are very distant from one another.
Still, the planets in our solar system are sufficiently massive and they are sufficiently close so that their interactions with one another produce nonelliptical orbits. However, these deviate only very slightly from those given by Kepler's laws. These deviations became measurable as telescopes improved, which is just another example of how technology drives scientific advancement.
In this case, the effects are small enough that they can be treated as approximately as “perturbations” to the two-body Keplerian orbits. In 1747, the Swiss mathematician Leonhard Euler (1707–1783) (pronounced “Oiler”) developed a technique that won for him a prize the Academy of Sciences of Paris had offered for developing analytical methods for calculating the motions of Jupiter and Saturn. Euler laid the groundwork for perturbation theory, which is still a major tool used in physics for solving by a sequence of approximations problems that cannot be solved exactly. And this method is not limited to celestial mechanics. For example, the highly successful theory of quantum electrodynamics, developed by physicists in the late 1940s, is based on calculating a series of increasingly accurate perturbation approximations.
One can imagine that other star systems might exist in the universe where the interactions of other planets cannot be treated as small perturbations. In that case, perturbation theory would produce such inaccurate predictions of planetary motion as to be worthless. And only the two-body problem can be solved exactly. Astronomers in those planetary systems would be forced to use numerical techniques to calculate orbits, but they could do this if they had computers at least as advanced as ours are today.
While his calculations were only partially successful, Euler set the stage for the methods developed by the French mathematician, astronomer, and physicist Pierre-Simon Laplace (1749–1827) in his five-volume tome Mécanique céleste (Celestial Mechanics) published between 1799 and 1805.
The equations of celestial mechanics were also worked out by another great French mathematician, astronomer, and physicist, Joseph-Louis Lagrange (1736–1813), who was born Giuseppi Luigi Lagrangcia of Italian parents in Torino, Italy. His treatise Mécanique analytique (Analytic Mechanics), first published in 1788, placed Newtonian mechanics on a comprehensive mathematical footing. Lagrange's equations still provide the means for students to solve problems in Newtonian mechanics in the most general way, independent of the choice of coordinate system. Furthermore, today many physics models, including those in relativistic quantum field theory, start by writing down a mathematical function called the Lagrangian.
Recall, Newton recognized that his derivation of Kepler's laws was based on the two-body assumption, which made it mathematically tractable. From the limited data available to him at the time, he concluded that because of all the random interactions between planets, the solar system could not retain its stable, predictable behavior by gravitational forces alone. And so, Newton conjectured, God had to step in occasionally to correct their motions.
A century later, Laplace and Lagrange independently calculated the long-term variations in a planet's semimajor axis resulting from the effects of perturbations by the other planets. Their calculations showed that, up to the first order in the masses of the planets, these variations vanish. Later still, the French mathematicians Siméon Denis Poisson (1781–1840) and Henri Poincaré (1854–1912) would show that this result remains true through the second order in the masses of the planets, but not through the third order.1 In short, the solar system is pretty stable but not ultimately so.
Laplace was able to account for all of Ptolemy's observations within a minute of arc, including the motions of Jupiter and Saturn that were inconsistent with previous calculations. Thus, Laplace showed that Newton's laws were, in themselves, sufficient to explain the movement of the planets throughout previous history.2 This led him to propose a radical notion that Newton had rejected: nothing besides physics is needed to understand the physical universe.
Like Lagrange, Laplace's name also appears frequently in physics, engineering, and mathematics classrooms, where students use the Laplacian in calculus problems and perform Laplace transformations in electrical-engineering classes. Poisson and Poincaré are names that are also prominently represented in these classes.
However, physics students usually do not hear, at least in the physics classroom, the story of Laplace's encounter with the emperor Napoleon in or about 1802. Physics professors generally avoid lecturing about anything that can't be calculated. Here's one version, but it is still disputed and the whole story is probably apocryphal:
Laplace had an audience with Napoleon and presented him a copy of Mécanique céleste. Someone had told Napoleon that the book contained no mention of God. Napoleon received it with the remark, “M. Laplace, they tell me you have written this large book on the system of the universe, and have never even mentioned its Creator.” Laplace, answered, “Je n'avais pas besoin de cette hypothèse-là.” (“I had no need of that hypothesis”). Napoleon, greatly amused, told this reply to Lagrange, who exclaimed, “Ah! c'est une belle hypothèse; ça explique beaucoup de choses” (“Ah, that's a beautiful hypothesis; it explains many things”).
Laplace never wrote anything denying the existence of God, and he may have been a deist. As discussed in the previous chapter, deism—as opposed to theism—supposes a creator god who set the universe in motion and then left it alone to carry out the instructions coded into the natural laws by that god. The quotation above, if true, may simply say that Laplace did not need to hypothesize anything beyond the laws of mechanics and gravity to describe the motions of the heavenly bodies.
In his 1796 book Exposition du système du monde, Laplace quotes Newton as saying, “The wondrous disposition of the Sun, the planets and the comets, can only be the work of an all-powerful and intelligent Being.” Laplace expresses the deist position when he comments that Newton “would be even more confirmed, if he had known what we have shown, namely that the conditions of the arrangement of the planets and their satellites are precisely those which ensure its stability.”3
Laplace agreed with Leibniz's criticism of Newton: “This is to have very narrow ideas about the wisdom and the power of God…that God has made his machine so badly that unless he affects it by some extraordinary means, the watch will very soon cease to go.” We will see this mistake being made today by those who say that the universe created by God is so imperfect that he had to fine-tune it so that life could evolve. Laplace and Leibniz would counter, “God is smarter than that.” I would put it another way: the universe is smarter than that.
LAPLACE'S DEMON
Whatever his religious proclivities, Laplace laid out the principle that became known as the clockwork universe or, alternatively, the Newtonian world machine: the universe is like a giant machine or clockwork, operating according to the laws of physics so that everything that happens is predetermined by what happened before.
Here's how Laplace expressed it in A Philosophical Essay on Probabilities:
We may regard the present state of the universe as the effect of its past and the cause of its future. An intellect which at a certain moment would know all forces that set nature in motion, and all positions of all items of which nature is composed, if this intellect were also vast enough to submit these data to analysis, it would embrace in a single formula the movements of the greatest bodies of the universe and those of the tiniest atom; for such an intellect nothing would be uncertain and the future just like the past would be present before its eyes.4
This “intellect” is usually referred to as Laplace's demon, although he did not use the term. Laplace just called it “an intellect” and did not associate it with any god. While not at odds with a creator deist god, the clockwork universe is clearly incompatible with the Judeo-Christian-Islamic God, or any other supreme being that is believed to not only create the universe but also play a major role in the operation of the universe after it is created, stepping in constantly to change the course of events—as Newton believed.
Deism became prominent during the period called the Enlightenment in the eighteenth century when science and reason began to hold sway over theology and revelation. Deists, following the previously cited opinions of Leibniz and Laplace, regarded it as illogical that a perfect god needed to step in at any time after the creation to fix things that may have gone awry.
Many prominent people of the time either were avowed deists or were regarded as deists based on their published views. In Europe these included Adam Smith (1723–1790), Frederick the Great (1712–1786), James Watt (1736–1819), and Voltaire (1694–1778). In America, Benjamin Franklin (1706–1790), Thomas Paine (1737–1809), and at least the first four presidents: George Washington (1732–1799), John Adams (1735–1826), Thomas Jefferson (1743–1826), and James Madison (1751–1836) were deists.
However, the Enlightenment and its version of deism did not survive into the nineteenth century for a lot of reasons that had little to do with Laplace's demon. The impersonal deist god did not provide the comfort of religion sought by the average person. Christian revivalism, which appealed to rich and poor alike with emotion in place of reason, spread throughout Europe and America. At the same time, the intellectual world of art and literature reacted against scientific rationalization and replaced it with an emphasis on intuition and emotion that was termed Romanticism.
Unlike the American Revolution, the French Revolution, which also grew out of the Enlightenment, had been a disaster. Furthermore, the Industrial Revolution had greatly increased the wealth of the upper and middle classes, who then proceeded to make the lives of the working class miserable as they were forced to labor for long hours and meager pay in “dark Satanic mills,” as the poet William Blake (1757–1827) called the mines and factories. At least in the fields where they worked from dawn to dusk at the mercy of landowners, peasants breathed fresh air, ate fresher food, and drank clean water.
NINETEENTH-CENTURY ASTRONOMY
The nineteenth century saw many advances in astronomy as both technology and mathematical calculations continued to improve. Here I will briefly review some of the more-important developments.
Let's begin late in the eighteenth century to add one more contribution to cosmology by Laplace. In Exposition du système du monde mentioned earlier, Laplace provided a model of the formation of the solar system that explained a number of facts that had previously puzzled astronomers, in particular, why all the planets revolve around the sun in the same direction and in pretty much the same plane. Swedish philosopher Emanuel Swedenborg (1688–1772) had proposed the same model back in 1734 and Immanuel Kant followed up on Swedenborg's idea in 1755. Laplace put it on a mathematical footing. Called the nebular hypothesis, the model assumes that the solar system evolved from a rotating globular mass of incandescent gas. As it cooled, the mass contracted and successive rings broke off from its outer edge. These rings cooled and condensed into the planets, with the remaining central core becoming the sun.
While Laplace's model was widely accepted in the nineteenth century, it was abandoned in the twentieth century when it could not explain the fact that the planets contain 99 percent of the angular momentum of the solar system. However, the notion of a rotating ball of gas is basically correct. Today's astronomers can see discs of diffuse material orbiting around young stars and protostars—objects in the process of becoming stars. Planets are believed to form in these disks as matter is pulled together into lumps by gravity. However, the theory still has problems with the formation of gas giants such as Jupiter and Saturn.
In 1801, the French astronomer and popularizer Joseph Jérôme Lefrançois de Lalande (1732 –1807) published a catalogue of over forty-seven thousand stars. By that time he had led an illustrious life, and this may be a good time to take a break from all these scientific details to talk about him personally because he was quite an enjoyable character. Here's a description of his appearance:
He was an extremely ugly man, and proud of it. His aubergine-shaped skull and shock of straggly hair trailing behind him like a comet's tail made him the favourite of portraitists and caricaturists. He claimed to stand five feet tall, but precise as he was at calculating the heights of stars he seems to have exaggerated his own altitude on earth. He loved women, especially brilliant women, and promoted them in word and deed.5
Lalande published a Dictionary of Atheists, in which he wrote: “It is up to the scholars to spread the light of science, so that one day they may curb those monstrous rulers who bloody the earth; that is to say, the warmongers. As religion has produced so many of them, we may hope to see an end to that as well.” He amusingly remarked that his atheist views were his revenge against God who had made him so ugly.6
With initial approval, Lalande had included Napoleon in his dictionary. But, then, the emperor realized he needed the Church's support and tried to have the astronomer censured by the Institut de France. Lalande refused to stop presenting his atheistic views. Even under a dictator, France remained remarkably intellectually free.
Getting back to the science stuff, in 1802 the English physicist and chemist William Wollaston (1766–1828) observed dark lines in the optical spectrum of the sun. These Fraunhofer lines are named after the German physicist Joseph von Fraunhofer (1787–1826), who studied them systematically in 1814. Almost half a century later, German physicist Gustav Kirchhoff (1824–1887) and German chemist Robert Bunsen (1811–1899) associated the dark Fraunhofer lines with the bright lines observed in the emission spectra of various heated elements.
Thus began the science of spectroscopy, which would become a major tool enabling astronomers to identify the chemical elements in stars and the interstellar medium. The second element in the chemical periodic table, helium, got its name since it was identified by its absorption lines in light from the sun before being discovered on Earth.
The mechanism for the generation of line spectra would not be discovered until 1913 when Niels Bohr used the new quantum theory to calculate the spectrum of hydrogen (see chapter 5). In fact, these line spectra were a major anomaly that could not be explained by the wave theory of light and led to the development of quantum mechanics.
In the meantime, the spectroscopy of stars further established the universality of physics. Newton had made the first great leap in that direction with his universal law of gravity. Previously, it had been assumed that one set of laws applied on Earth and another set in the heavens. Newton proposed that the force that causes an apple to fall from a tree to the ground was the same force that caused the moon to fall around Earth. With the observation that the spectral lines from stars were the same as observed from hot gases in laboratories on Earth, the universality of physics was corroborated. Physics is the same throughout the universe.
Bessel functions are very familiar to students of physics, engineering, and mathematics. Although they were first introduced by physicist Daniel Bernoulli (1700–1782), they are named after astronomer Friedrich Wilhelm Bessel (1784–1846). Bessel was trained as an accountant and worked for a shipping company. His interest in navigation led Bessel into astronomy and in 1810 at age twenty-five he became the director of the Königsberg Observatory in Prussia.
Bessel was the first to use parallax to measure the distance to a star when, in 1838, he reported that 61 Cygni was 10.4 light-years away (1 light-year = 9.46 × 1012 kilometers). The current estimate is 11.4 light-years. Later that year, Friedrich Georg Wilhelm von Struve (1793–1864) and Thomas Henderson measured, respectively, the parallax of Vega (25 light-years away) and Alpha-Centauri (4.4 light-years away).
Figure 4.1 shows how parallax works. A star is viewed twice, six months apart. From the difference in the angles between the two lines of sight, θ (in radians) and the radius of Earth's orbit, r, the distance to the star (in small-angle approximation, which is good enough) is d = 2r/θ.
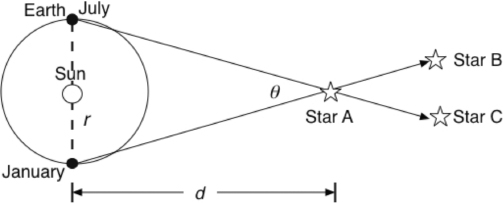
Figure 4.1. How parallax is used to determine the distance from Earth to a star or another astronomical object. The star A will appear at B in one time, and six months later at C. If the radius of Earth's orbit is r (distance to sun) and the measured parallax is θ, then the distance to the star is d = 2r/θ. Unlike depicted here, the angle θ is very small, so this small-angle approximation can be used. Image by the author.
In this way, humans began to learn about the immense distances of stars from Earth. Alpha-Centauri, a multiple-star system, is the closest. Well, except for the sun, which is 147 million kilometers or 1.55 × 10–5 light-years (8.17 light-minutes) away. At the time its distance was measured, the farthest known planet from the sun was Uranus. Although Uranus had been observed since ancient times, because of its dimness it was not established as a planet until 1781, by Herschel. Its distance from the sun at the farthest point in its orbit is 3.00 billion kilometers or 0.000317 light-years (2.78 light-hours).
This brings us to the next planet, Neptune. Galileo observed Neptune twice, in 1612 and 1613, but assumed it was a fixed star—although recent evidence suggests he may have noticed movement with respect to the stars. In the early 1800s, French astronomer Alex Bouvard (1766–1843) measured deviations from the then-standard tables on the orbit of Uranus. He proposed that an eighth planet beyond Uranus in the solar system was perturbing the orbit. British astronomer John Couch Adams (1819–1892), using various sources of data, made several estimates of where to search for the new planet.
Independently, the French mathematician Urbain Jean Joseph Le Verrier (1811–1877) was making similar calculations, and on August 31, 1846, he presented his final prediction to the French Academy. Two days later, Adams sent his final prediction to the Royal Greenwich Observatory. On September 18, Le Verrier sent his prediction to the Berlin Observatory. There, on September 23, the planet was found within one degree of Le Verrier's prediction and later identified with Neptune. Astronomers in Greenwich had dragged their feet, so Adams lost out. He graciously acknowledged Le Verrier's priority.
Neptune is 4.50 billion kilometers (0.000476 light-years or 4.17 light-hours) from the sun at its farthest point.
The next significant advance in nineteenth-century astronomy was made by English astronomer William Huggins (1824–1910) with his extensive measurements of the spectra of stars to determine their chemical composition. He demonstrated that the stars are composed of the same chemical elements as found on Earth. He discovered hydrocarbons in comets. And, most significantly, in 1868 Huggins was the first to measure the radial velocity (velocity component along the line of sight) of a star by assuming that the shifts observed in the spectral lines of stars were the result of the Doppler effect.
In 1842, Christian Andreas Doppler (1803–1853) had shown that the wavelength of a wave changes as the source of the wave moves toward or away from the observer. So, when a star is moving away from us, its visible light will be shifted toward the red end of the spectrum; when moving toward us, it will be shifted toward the blue. The amount of frequency shift enables the astronomer to calculate the radial velocity. Specifically, the redshift is defined as z = 1 + Δλ/λ, where Δλ/λ is the fractional shift in the wavelength. The radial velocity then is v = zc, where c is the speed of light, for v << c. The exact formula valid for all speeds is more complicated and derived from the special theory of relativity.
As we will see, the spectral-line shifts from astronomical objects would have profound consequences in the twentieth century when it was discovered that most galaxies were moving away from us and their redshifts are a measure of their distances. This led to the discovery that the universe is far larger than the few light-years to stars that could be measured by parallax.
While nineteenth-century astronomers were learning about the size of the universe, physicists were pondering the problem of the age of the sun and Earth. In 1863, British physicist William Thomson, Lord Kelvin (1824–1907), estimated the age of Earth assuming it was initially molten and gradually thickened as it cooled, coming up with twenty million years. In 1856, German physicist Hermann von Helmholtz, who had formulated the principle of conservation of energy, considered the age of the sun and suggested its energy arose from gravitational collapse as the decrease in potential energy provided the energy of the emitted light. In 1862, Kelvin used Helmholtz's approach to conclude that the sun could be no more than twenty million years old. These calculations were very crude, and the fact that Kelvin obtained the same number from each method was no doubt due to some mutual fudging. However, the solar calculation was the more reliable.7
In any case, both estimates meant big trouble for the theory of evolution by natural selection announced jointly by Charles Darwin (1809–1882) and Alfred Russel Wallace (1823–1913) in 1858. Evolution required a huge timescale of at least hundreds of millions of years. Darwin himself fretted over this discrepancy and considered it the most serious threat to his theory.
On the other hand, geologists supported the hypothesis of evolution with their estimates of the age of Earth of around two billion years. The problem would not be solved until early in the twentieth century with the discovery of nuclear fusion, which will allow the sun to shine for another five billion years or more. The age of Earth is now well determined from radioactive dating and is 4.54 billion years with an error of 1 percent.
In the meantime, observational astronomy continued to advance. In 1888, American astronomer James Keeler (1857–1900) used the large 36-inch refracting (lens-based) telescope at the Lick Observatory on Mount Hamilton in California to observe a gap in Saturn's rings.
On a smaller side hill, Keeler installed a 36-inch reflecting telescope and, for the first time, Newtonian reflecting telescopes began to appear on mountaintops with the result of a significant improvement in capability, especially for spectroscopy, which was greatly improved with the elimination of the spherical aberration intrinsic to lens-based telescopes.
However, Keeler did not get to spend much time observing with this instrument. Disagreement with the director of Lick, a rigid West Point graduate, caused Keeler in 1891 to move to Alleghany Observatory. There, despite far inferior instruments and the industrial skies of Pittsburgh, he was able to make a major discovery that brought him international notice. Using spectroscopy, Keeler confirmed the theory of James Clerk Maxwell (1831–1879) that the rings of Saturn were composed of small objects that rotated around the planet at different rates.
Called back in 1898 to take over the directorship of Lick from its unpopular director, Keeler rebuilt another 36-inch reflector called the Crossley telescope that had been donated to Lick by a British politician, Edward Crossley, and was widely regarded as a “piece of junk.” But Keeler fixed it up and when it was finally operative, he began taking beautiful photographs of spiral nebula. These would become the key to the next door to be opened on the cosmos. Unfortunately, Keeler was unable to walk through that door, dying in 1900 just short of his forty-third birthday.8