EVERYTHING EXPLAINED? NOT QUITE

In the previous chapter, we saw that by the end of the nineteenth century, physics had just about explained everything there was to explain about the physical world. The world was just particles moving and colliding with one another according to the laws of mechanics, gravity, and electromagnetism.

The renowned physicist Lord Kelvin (William Thomson) is often quoted as having remarked in an address to the British Association for the Advancement of Science in 1900, “There is nothing new to be discovered in physics now. All that remains is more and more precise measurement.” However, no evidence has been found to confirm this statement.¹ While Kelvin may not have said it, this expressed a common sentiment at the time. In any case, it wasn't factually true. As we have seen, in 1900 there were still several observations that could not be explained by the wave theory of light.

As was seen in the last chapter, nineteenth-century physics actually contradicted the notion of the ancient atomists of a universe composed of elementary particles moving around in an otherwise-empty void. The nineteenth-century cosmos was filled with a smooth, continuous, invisible medium called the aether in which particles moved.

Light was thought to be result from the vibration of the aether, just as sound waves arise from the vibrations of media such as air and water. The fact that air and water are not completely smooth and continuous but made of tiny atoms was not a concern since sound waves can be derived from Newtonian particle mechanics applied to discrete media. Indeed, Michael Faraday speculated that the aether might also be particulate, as did Isaac Newton before him. What's more, recall that James Clerk Maxwell did not assume the existence of the aether in deriving the existence of electromagnetic waves and that no one could find any evidence for the aether. Both theoretically and observationally, the aether did not appear to exist.

As for the rest of physics, the highly successful application of Newton's laws of motion and gravity to the motions of planets and apples demonstrated that those laws are universal. Similarly, the observation of the same spectral lines in stars as seen in laboratories on Earth demonstrated that they are based on equally universal laws.

In this case, since light is an electromagnetic wave, we can conclude Maxwell's equations are also universal. However, these equations do not provide a mechanism for the observed narrow-line spectra. And, on top of that, the wave theory of light could not explain the blackbody spectrum or the photoelectric effect.

As for the particulate nature of atoms, we have seen that many scientists remained unconvinced because the evidence was indirect.

In the following sections, I will briefly summarize the revolutionary developments in physics in the period from 1900 to the end of World War II in 1945, with an eye toward their particular relevance to cosmology. For more detailed explanations, you may refer to God and the Atom.

SPECIAL RELATIVITY

In 1905, Albert Einstein published his special theory of relativity and in the process revolutionized our concepts of space, time, and matter. Albert Michelson and Edward Morley had failed to find evidence for the variation in the speed of light expected from Earth's motion through the hypothesized aether. While Einstein does not mention that result in his paper, he likely knew about it. However, instead of referring to any observations, Einstein made a purely theoretical argument—although it is important to remember that the theory was ultimately based on observed phenomena, namely, electricity and magnetism.

The electromagnetic waves derived from Maxwell's equations traveled exactly at the speed c in a vacuum, in apparent violation of Galileo's principle of relativity that, as we saw in chapter 2, asserts that all velocities are relative. So the relative velocity between a source of light and its observer should add or subtract from c to give an observed speed different from c. However, Maxwell's equations did not allow this and Michelson and Morley did not see it.

THE RELATIVITY OF TIME AND SPACE

Einstein was not ready to give up on the principle of relativity. So he asked what would be the consequences if (1) the principle of relativity is valid and (2) the speed of light in a vacuum is always c. From these two axioms, Einstein showed, among other results, that the time and distance intervals between two events are not invariant. That is, two observers in reference frames moving with respect to each other will measure different time and spatial intervals.

In other words, time and space are not absolute—as common sense dictates. A clock moving with respect to an observer will be seen by that observer to slow down (time dilation); an object moving with respect to an observer will be seen by that observer to contract in the direction of its motion (Fitzgerald-Lorentz contraction). That doesn't mean that they really do these things. Clocks don't slow down for observers sitting on the clocks, and objects don't contract for observers sitting on the objects. The just appear to do these weird things to outside observers in other reference frames.

Of all Einstein's revolutionary discoveries, his deconstruction of the commonsense view of time was probably the most profound. Nothing seems so ubiquitous—so absolute and universal—as time. Yet special relativity called into question some of our deepest intuitions of time. No moment in time can be labeled a universal “present.” There is no past or future that applies to every point in space. Two events separated in space can never be judged to be objectively simultaneous, valid in all reference frames.

Time dilation is important only when the relative speeds of clocks are near the speed of light or when making highly precise measurements with atomic clocks. So these effects were not noticed in everyday life. However Einstein's theory has been confirmed by a century of experiments involving high-energy particles that move near the speed of light, as well as low-speed measurements with atomic clocks. Today everyone with a smartphone or Global Positioning System (GPS) in his car is relying on Einstein's theory, which, as we will see, also must take into account the general theory of relativity.

While we do not need to worry about the relativity of time in the social sphere, it is important not to make universal, philosophical, or metaphysical inferences from the limited range of everyday human experience.

Philosophers and theologians have introduced alternate “metaphysical times” more along the lines of common experience, but these have no connection with scientific observations and have no rational basis outside the realm of speculative theology. Scientific models uniformly assume that time is, by definition, what is measured on a clock and that time is relative.

TIME AND SPACE DEFINED

Until recently, the passage of time was registered by familiar regularities such as day and night and the phases of the moon, or more accurately by the apparent motions of certain stars. The second was defined by the ancient Babylonians to be 1/84,600 of a day. Our calendars are still based on astronomical time using the Gregorian calendar, introduced in 1582, in which the year is defined as 365.2425 days (see chapter 2). With the rise of science, the second has undergone several redefinitions to make it more useful in the laboratory.

The most recent change occurred in 1967 when the second was redefined by international agreement as the duration of 9,192,631,770 periods of the radiation corresponding to the transition between the two specific energy levels of the ground state of the cesium-133 atom. The minute remains sixty seconds, the hour remains sixty minutes, and the day remains twenty-four hours, following ancient traditions. The day is still taken to be 84,600 seconds, as in ancient Babylonia. Our calendars need to be corrected occasionally to keep them in harmony with the seasons because of the lack of complete synchronization between atomic time and the motions of astronomical bodies.

Note that we should not assume that the time measured on atomic clocks is some kind of “true time.” It is no less arbitrary than astronomical time, time measured with a pendulum, or time defined, for example, by my personal heartbeats. However, by using atomic time rather than heartbeat time, the models that use time are much simpler and don't have to make constant corrections for my daily activity. More seriously, atomic time also avoids the corrections we have to make when we use astronomical time, which has its own small but significant irregularities.

Until Einstein came along, it was generally assumed that space and time were two independent properties of the universe. Until 1983, the standard unit of length, the meter, was defined as the length of a certain platinum rod stored under carefully controlled conditions in Paris. With the help of mathematician Hermann Minkowski (1864–1909), Einstein had formulated the special theory in terms of a four-dimensional space-time in which time is the added dimension. By 1983, relativity had become so well-established empirically that the meter was refined so that it, like time, was defined by what is read on a clock. Currently the meter is defined as the distance between two points in space when the time it takes light to go between the points in a vacuum is 1/299,792,458 second.

Note that this implies that the speed of light in a vacuum is c = 299,792,458 meters per second by definition. Many physicists and most other scientists still seem to think that c is a quantity that might be variable, changing with time or location. This is impossible because it has the value it has by definition.

THE RELATIVITY OF ENERGY AND MOMENTUM

Einstein found that energy and momentum are also relative. However, mass is invariant, that is, the same in all reference frames. In units where c = 1, we have a simple relationship between mass, energy, and momentum that define the inertial properties of a body and show their connection. The mass m of a body with energy E and momentum p is given by the equation: m² = E²–p². When a body is at rest, p = 0 and the rest energy of a body is just equal to its mass m. This is the result that is more famously written E = mc².2

Another famous result of special relativity is that a body with mass cannot be accelerated to or past the speed of light. That is, there exists a universal speed limit, c. Here I need to clear up another common misconception. Special relativity does not forbid particles from traveling faster than light, as long as they never go slower. Such particles are called tachyons. But they are still hypothetical; none have ever been observed.³

The special theory of relativity requires a different set of equations for most of the quantities associated with particle motion when the speeds of the particles are close to the speed of light. However, rest assured that these equations revert to the familiar Newtonian equations when the speeds are low compared to light.

With special relativity, Einstein eliminated the aether and restored Democritus's void to the cosmos, solving the empirical anomaly reported by Michelson and Morley and the theoretical problem with Maxwell's theory of electromagnetic waves. They are fully consistent with the principle of relativity. All speeds are still relative—except the speed of light. And that, as just shown, is an arbitrary number that just decides what units you want to use for distance and time. Throughout this book I mostly use c = 1 light-year per year.

GENERAL RELATIVITY

In November 1907, Einstein was sitting in his chair in the patent office in Bern when, he later described,

All of a sudden a thought occurred to me. “If a person falls freely he will not feel his own weight.” I was startled. This thought made a deep impression on me. It impelled me toward a theory of gravitation.4

Einstein's theory of gravity would not be published until 1916 as the general theory relativity. Special relativity only applied to reference frames moving at constant velocity. Einstein was able to include acceleration in a new theory of gravitation that predicted tiny effects that could not be understood with Newton's theory.

Let me put Einstein's insight in the following terms: An observer inside a closed capsule in free fall would not be able to distinguish that situation from one in which she is in the same capsule out in space far away from any planets or stars. Furthermore, if the capsule in space were accelerated, say by a rocket motor, with the same acceleration an object has when falling to the ground, like the apple that fell on Newton, then she could not tell the difference between that and just sitting still on the surface of the Earth. So acceleration and gravity are in a sense equivalent.

Now, the observer in the capsule could make delicate measurements of the paths of falling bodies, which would converge along lines pointing to the center of Earth when her capsule is sitting on the surface. If, on the other hand, the capsule were accelerating out in space, the lines would all be parallel. So the equivalence of the two pictures technically applies only for an infinitesimal region of space. This principle is what we call “local.”

In the model of gravity developed by Einstein, the force of gravity is basically done away with. A body free of any forces follows a geodesic path through non-Euclidean space-time, analogous to an aircraft following a great circle from one point on Earth's surface to another in order to minimize the distance traveled. Earth falls around the sun in an ellipse because that's the geodesic path around a massive object.

Einstein wrote an equation that allowed him to calculate the shape of space-time and the geodesics from the distribution of matter in space:

(curvature of space-time) = (density of matter)

Einstein was troubled by the fact that purely attractive gravity would cause the universe to collapse. At the time, everyone thought the universe was a static firmament, as described in the Bible. So Einstein added another term, Λ, to his gravitational equation called the cosmological constant (CC).

(curvature of space-time + cosmological constant) = (density of matter)

So the CC acts as another component of the curvature of space-time, which could be either positive or negative. When Λ is positive, the result is a gravitational repulsion that Einstein thought would stabilize the universe.

Note that the cosmological constant could just as well have been put on the right-hand side of the equation as part of the density of matter:

(curvature of space-time) = (density of matter – cosmological constant)

But it's still the same equation, which works equally well either way. This is an example of why it is a mistake to take the elements of mathematical models and try to attribute metaphysical reality to them. Is the cosmological constant “really” part of the curvature of space-time or is it “really” part of matter? It doesn't matter. It's just a human contrivance and either choice gives the same empirical result.

General relativity predicted several phenomena that could not be explained with Newtonian gravity. One of these had already been observed for quite a while and was another empirical anomaly that could not be explained by nineteenth-century physics. In 1859, Urbain Le Verrier, who was mentioned in chapter 3 as the discoverer of Neptune, determined from already-recorded observations that the rate of precession of the perihelion of Mercury differed from that calculated from Newtonian theory by 38 seconds of arc per century, later revised to 43 seconds. In November 1915, Einstein applied his new general theory to the problem and obtained this exact number. He was so excited by this result that, he said, he had “heart palpitations.”⁵

Einstein also predicted the light would be deflected by the sun. This was an old idea, going back to Newton. In a note at the end of Opticks, published in 1704, Newton suggested that the particles in his corpuscular theory of light should be affected by gravity just as ordinary matter. In 1801, German astronomer and physicist Johann Georg von Soldner (1776–1833) calculated from Newtonian physics that the deflection of a beam of corpuscles skimming along the surface of the sun would be 0.9 arc-seconds. However, a measurement of such a small angle was not technically feasible at the time and, as we have seen, in the early nineteenth century Newton's corpuscular theory of light was discarded in favor of the wave theory.

Einstein calculated an effect twice the Soldner value, in disagreement with Newtonian gravity. On May 29, 1919, two British expeditions took photographs of the region around the sun during a total solar eclipse and compared them with pictures taken from the same locations in July. The famous British astronomer Arthur Eddington led the expedition to Principe Island in Africa and claimed to confirm Einstein's calculation. The independent expedition to Sobral, Brazil reported a result closer to Soldner's value. However, the astronomy community sided with Eddington based on what they saw were defects in the Sobral telescopes, and based perhaps on a little more respect for Eddington's authority.

Eddington's announcement in 1919 made headlines around the world and, more than anything, transformed Einstein into the twentieth-century icon he became. He is the only scientist ever honored by a Manhattan ticker-tape parade, which occurred during his visit there in 1921.

Eddington's measurements were also challenged, but Einstein's calculation has been verified many times over since. One of the most popular science cruises today is to witness a total solar eclipse when it occurs, as they often do, in the middle of an ocean. Astronomers don't require much arm-twisting to join these cruises, all expenses paid, where they give a few lectures and make some observations while enjoying all the amenities.

Allow me to indulge in a little “what-if?” Suppose the gravitational deflection of light had been observable in 1804. Then the wave theory of light would have been falsified at that time since it produces no effect, while at least the Newtonian corpuscular theory is within a factor of two, quite respectable for such a tiny effect. Now the deflection of light by gravity joins line spectra, blackbody radiation, and the photoelectric effect in convincingly falsifying the wave theory of electromagnetic radiation.

Einstein also predicted that a clock in a gravitational field runs slower, as observed by someone outside the field. This is called gravitational time dilation and is derived directly from general relativity. This effect is also well confirmed. If the GPS in your car did not correct for gravitational time dilation, it would not always take you to where you want to go.

Gravitational time dilation also implies that light (or any electromagnetic “wave”) will decrease in frequency when it moves away from a massive body. Viewed in terms conservation of energy, the kinetic energy of a photon is equal to hf, where f is the frequency of the corresponding electromagnetic wave, where h is Planck's constant, to be defined later. As a photon moves away from the body it gains potential energy and so it loses kinetic energy to compensate and so decreases in frequency.

Since Einstein's original predictions almost a century ago, general relativity has been submitted to many tests of ever-increasing sophistication. It remains consistent with all observations involving gravity today.6

BLACK HOLES

As far back as the eighteenth century, John Michell (1724–1793) and Pierre-Simon Laplace noted that a gravity field of a body could be so great that light could not escape. In 1916, Karl Schwarzschild showed from general relativity that if a body of mass M with a radius less than R_s = 2GM/c² will not allow light to escape. For an object with the mass of the sun, the Schwarzschild radius is about three kilometers. In 1967, physicist John Wheeler dubbed these objects “black holes.” As we will see, plenty of evidence now exists for black holes and most, if not all, major galaxies, including our Milky Way, have supermassive black holes at their centers.

In 1974, Stephen Hawking showed that black holes actually radiate photons so that they are all ultimately unstable and eventually decay away.⁷ However, the lifetimes for black holes of astronomical size is very long. A black hole of solar mass will last 10⁶³ years. Microscopic black holes, on the other hand, have very short lifetimes, and although searches for the expected radiation have been conducted, none has yet been observed.

NOETHER'S THEOREM

On March 23, 1882, a girl named Emmy Noether was born in Erlangen, Bavaria. The daughter of a mathematician, she would turn out to be a mathematical genius and make one of the most important contributions to physics in the twentieth century. Its impact is only now beginning to be fully appreciated. Noether would be considered one of the foremost heroines of the twentieth century had more people understood mathematics and physics.8

In 1915, Noether published a theorem that completely transformed our philosophical understanding of the nature of physical law. Until I learned about it, I always thought, as most scientists still do, that the laws of physics are restrictions on the behavior of matter that are somehow built into the structure of the universe. Although she did not put it in those terms, Noether showed otherwise.

Noether proved that for every continuous space-time symmetry there exists a conservation principle.

Three conservation principles form the foundational laws of physics: conservation of energy, conservation of linear momentum, and conservation of angular momentum. Noether showed that conservation of energy follows from time-translation symmetry; conservation of linear momentum follows from space-translation symmetry; and conservation of angular momentum follows from space-rotation symmetry.

What this means in practice is that when a physicist makes a model that does not depend on any particular time, that is, one designed to work whether it is today, yesterday, thirteen billion years in the past, or thirteen billion years in the future, that model automatically contains conservation of energy. The physicist has no choice in the matter. If he tried to put violation of energy conservation into the model, it would be logically inconsistent.

If another physicist makes a model that does not depend on any particular place in space, that is, one designed to work whether it is in Oxford, in Timbuktu, on Pluto, or in the galaxy MACS0647-JD that is 13.3 billion light-years away, that model automatically contains conservation of linear momentum. The physicist, once again, has no choice in the matter. If she tried to put violation of linear-momentum conservation into the model, it would be logically inconsistent.

Similarly, any model that is designed to work with an arbitrary orientation of a coordinate system, to work whether “up” is defined in Iceland or Tasmania, must necessarily contain conservation of angular momentum.

Since these three principles form the basis of classical mechanics, it can be said that they are not “laws” that govern the behavior of matter. Rather, they are human artifacts that follow from symmetry principles that govern the behavior of physicists, forced on them if they want to describe the world objectively. There is no reason to think that the laws of physics are the construction of an extraphysical lawgiver.

As we will see in a later chapter, Noether's theorem can be generalized into a principle called gauge invariance from which most of the basic laws of physics can be derived. For example, charge conservation and Maxwell's equations result from the gauge symmetry of electromagnetism. I will defer the discussion of the philosophical implications of this notion until that time.

QUANTUM MECHANICS

The twentieth century began in 1900 with Max Planck providing a model that quantitatively described the blackbody radiation spectrum, illustrated in figure 6.1 for the specific case of the sun. (I know, the sun is yellow; but it is a blackbody by definition since it does not reflect light.) The model was based on the hypothesis that light is not continuous but occurs in bundles of energy Planck called quanta. These quanta carried energies that were proportional to the frequency f of the radiation. The proportionality h, now called Planck's constant, Planck obtained numerically by adjusting it to fit the spectral data. Recall that the frequency of light is related to its wavelength λ by λ = c/f, where c is the speed of light.

The ultraviolet catastrophe of classical wave theory discussed in chapter 5 is avoided by energy conservation. The lower-wavelength end of the spectrum corresponds to higher-energy quanta and, since a body contains only so much energy, the spectrum must fall off at short wavelengths. Also, the wavelength of the spectral peak decreases with temperature because, as we saw in the discussion of statistical mechanics in chapter 5, temperature is a measure of the average kinetic energy of a body. That is, the hotter a body, the lower will be the wavelength of the spectral peak—or the higher the frequency of that peak.

In the same amazing year of 1905 when he introduced relativity, Einstein carried Planck's idea further and proposed that light is composed of particles, later dubbed photons, whose energy is proportional to the frequency of the corresponding electromagnetic wave. That is, if f is the frequency of the wave, the energy of each photon in the wave is E = hf, where h is Planck's constant. Using this assumption, Einstein as able to explain the photoelectric effect. An electric current is produced when photons kick electrons out of a metal. In order to do this, they need a minimum energy, which is why there is a threshold—a minimum frequency at which the current is produced. In 1914, American physicist Robert Millikan) confirmed Einstein's proposal in the laboratory.

Einstein showed that light is not the vibration of the aether or any other medium but a stream of particles, just as Newton claimed in his corpuscular theory of light. But, if light is corpuscular, then how can it produce the wavelike effects seen in interference and diffraction experiments?

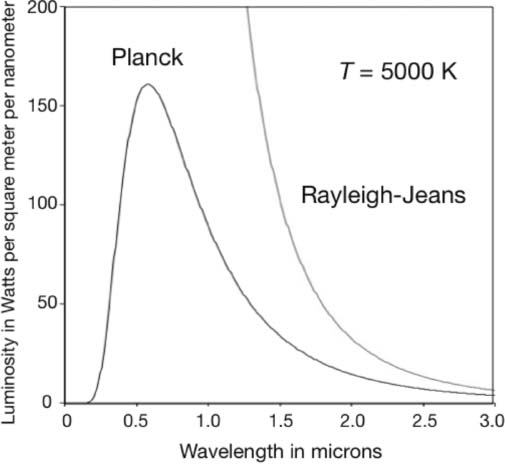
Figure 6.1. The intensity spectrum of a spherical blackbody with an absolute surface temperature T = 5000 K as a function of wavelength. Shown here is the ultraviolet catastrophe predicted by classical wave theory, the Rayleigh-Jeans law, which was discussed in chapter 5. The Planck prediction agrees with the data. The wavelength scale is given in microns or millionths of a meter, and the radiation luminosity scale is in units of kilowatts per square meter per nanometer. Image by the author.

French physicist and aristocrat Louis de Broglie provided the answer in 1924 in his doctoral thesis: all particles have wavelike properties. De Broglie noted that a photon of momentum p has an associated wavelength λ = h/p. He hypothesized that this relation holds for all particles, in particular, electrons. This is called the de Broglie wavelength.

De Broglie's conjecture was verified in 1927 when American physicists Clinton Davisson and Lester Germer observed the diffraction of electrons beamed onto the surface of a nickel crystal.

And so not only photons but also electrons and ultimately all particles have wavelike properties. This is known as the wave-particle duality. However, here we have another physics result that is widely misunderstood, even among physicists. You often hear, “An object is a particle or a wave depending on what you decide to measure.” This is wrong. No one has ever measured a wavelike property associated with a single particle. Interference and diffraction effects are only observed for beams of particles and only particles are detected, even when you are trying to measure a wavelength. The statistical behavior of these ensembles of particles is described mathematically using equations that sometimes, but not always, resemble the equations for waves.

If you do an interference or diffraction experiment in which you detect individual photons, you will not see the effect until you accumulate a large number of detections. For example, you could do a double-slit interference experiment with a beam of photons of one per day. Watch it for a year, and you will see the interference pattern develop. Note that the photons can hardly be said to be “interfering with each other,” which is often the way the effect is described.

If you object to me calling one photon a day a “beam,” where do you draw the line where a beam suddenly appears? One per hour? One per second? One per nanosecond?

Let me make this is explicit as I can: It is incorrect to say, “this photon has a frequency f” or “this electron has a wavelength λ.” The correct statements are: “this photon is a member of an ensemble of photons that can be described statistically as a wave of frequency f” and “this electron is a member of an ensemble of electrons that can be described statistically as a wave of wavelength λ.”

In 1926, Austrian physicist Erwin Schrödinger produced a mathematical theory called wave mechanics in which he associated particles with a complex number called the wave function.9 The same year, German physicist Max Born gave the now generally accepted interpretation in which the square of the magnitude of the wave function gives the probability per unit volume for finding a particle at a particular position at a given time. Nothing in quantum mechanics predicts the behavior of a lone particle—consistent with the interpretation of the wave-particle duality given previously.

A year earlier, in 1925, German physicist Werner Heisenberg had produced the first version of what has come to be called quantum mechanics that makes no use of waves and instead applies the mathematics of matrix algebra. After some initial controversy as to which formulation was better, Schrödinger showed that they were mathematically equivalent. Both the Heisenberg and Schrödinger formulations applied only to nonrelativistic particles, that is, those moving at speeds much less than the speed of light. That is, they could be used to describe slow-moving electrons but not photons.

In 1927, British physicist Paul Dirac, whose genius came close to matching Einstein's, formulated a quantum theory of photons. The next year, he produced a relativistic theory of electrons that predicted the existence of antimatter. In 1932, American physicist Carl Anderson reported the detection of particles in cosmic rays that looked like electrons but curved opposite to the direction of electrons in a magnetic field and so had to have positive electric charge. Anderson associated the particles with Dirac's antimatter and dubbed the antielectrons positrons.

In 1930, Dirac published the definitive work on quantum mechanics titled The Principles of Quantum Mechanics.10 In the book, which has gone through many editions and printings since, he does away completely with the wave function, replacing both wave mechanics and matrix mechanics with more-powerful linear vector algebra. While most chemists and those physicists who deal just with low-energy phenomena can get by with less-sophisticated Schrödinger wave mechanics, Dirac's quantum mechanics is necessary for understanding the behavior of elementary particles and high-energy phenomena in general.

While special relativity has been successfully reconciled with quantum mechanics, general relativity has not been. In particular, important for our cosmological story, general relativity does not apply to the earliest moments of our universe when quantum effects predominate. As we will see, this has not stopped religious apologists from using general relativistic arguments to claim evidence for a divine creation of the universe.

THE PLANCK SCALE

At this point I would like to introduce a concept that will be increasingly important as we get deeper into cosmology. As I have emphasized, every quantity in physics that directly relates to observations is operationally defined by how it is measured with a well-prescribed measuring apparatus. We have seen that both time and distance intervals are defined by what is measured on a clock, where the distance between two points is the time measured for light to pass between these points in a vacuum.

It can be shown that the smallest possible time interval that can be measured is the Planck time, 5.391 × 10^–44 second, and the shortest possible distance interval that can be measured is the Planck length, 1.616 × 10^–35 meter.11

Another important quantity is the Planck mass, 2.177 × 10^–8 kilogram. The Schwarzschild radius for a sphere with a mass equal to the Planck mass is twice the Planck length, which implies that it is a black hole (see earlier discussion on black holes). The Planck energy is then defined as the rest energy of a body with the Planck mass, which is 1.221 × 10²⁸ electron volts. An electron volt is the energy gained by an electron in dropping through an electric potential of one volt. We will use this unit of energy frequently, abbreviated eV.

ATOMS AND NUCLEI

In De rerum natura, mentioned in chapter 1, Lucretius described the zigzag motion of dust motes in a sunbeam and argued that it is caused by atoms colliding with the motes in the beam. In 1857, the Scottish botanist Robert Brown (1773–1858) observed pollen grains zigzagging in water and the effect came to be known as Brownian motion. In a third paper in 1905, Einstein derived equations that showed how the existence and scale of atoms could be demonstrated from the jaggedness of the paths of Brownian grains. In 1909, French physicist Jean Baptiste Perrin applied Einstein's theory as well as other techniques to measure Avogadro's number, an important constant in chemistry that, for our purposes, we can simply view as the number of atoms in a gram of hydrogen gas. The current value is 6.022 × 10²³, the reciprocal giving the mass of the hydrogen atom, 1.66 × 10^–24 gram. Although this measurement was still indirect, at this point only the most obdurate holdouts, such as Ernst Mach, could still deny that matter is composed of huge numbers of tiny particles.

In 1896, French physicist Henri Becquerel (1852–1908) discovered that the element uranium emitted previously unobserved penetrating radiation. Further laboratory experiments by Becquerel, Ernest Rutherford, Pierre Curie, and Marie Curie identified three types of radiation from a number of different elements: α, β, and γ.

In 1909, Hans Geiger and Ernest Marsden bombarded gold foil by α-radiation from radon gas, which showed surprisingly large deflections of the paths of the rays as they scattered off the foil. In 1911, Rutherford inferred from these observations that the atom, tiny as it already is, has an even tinier nucleus, much smaller than the atom itself, containing most of the mass of the atom. In the model, electrons circle about the nucleus in planetary-like orbits.

In 1913, Danish physicist Niels Bohr proposed that electrons in atoms could exist only in certain orbits. Each orbit corresponded to a specific energy level, with the ground state the lowest energy. When an electron in an atom drops from a higher to a lower level, a photon of a very precise energy equal to the energy difference between the levels is emitted, which appears as a very narrow line in the emission spectrum. Bohr was able to calculate the observed emission spectrum for hydrogen. The absorption spectrum followed since only photons with energies exactly equal to the differences between levels will be absorbed. In this way, the final anomaly from nineteenth-century physics that could not be accounted for in the wave theory was solved; the narrow line spectra of atoms was explained.

Bohr's theory was very crude but remarkably agreed with the data. The quantum mechanics of both Heisenberg and Schrödinger obtained the same hydrogen energy level formula as Bohr's and offered the opportunity to be applied to other atoms. Dirac's relativistic quantum theory did even better by calculating the small splittings of spectral lines called fine structure that were observed as spectroscopic instruments improved.

Dirac's theory also proved that the electron has half-integer spin, where spin is the name for a particle's intrinsic angular momentum. This notion had been earlier conjectured by Austrian physicist Wolfgang Pauli.12 In 1925, Pauli had proposed what is now called the Pauli exclusion principle: two identical particles of half-integer spin cannot simultaneously occupy the same quantum state. With this principle, it became possible to explain the periodic table of the chemical elements.

While we still call the chemical elements “atoms,” they are no longer irreducible when we move from low-energy chemical reactions to high-energy nuclear reactions. The chemical atoms are not pointlike particles but composite structures of more-elementary objects, nuclei and electrons. Furthermore, they can be transmuted from one type to another in nuclear reactions, fulfilling the alchemist's dream.

In the 1930s, nuclei themselves were shown to be composed of more-fundamental objects, protons and neutrons, where the neutron is just slightly heavier than the proton and electrically neutral—although it is a tiny magnet, as are the proton and electron. The proton is positively charged. Hydrogen is the simplest element, made of a proton and an electron. Add a neutron to its nucleus, and you have heavy hydrogen or deuterium. Add another neutron, and you have tritium. Add another proton to tritium, and you have helium.

Each element in the periodic table is identified by an atomic number Z that is equal to the number of protons in its nucleus. It is also the number of electrons in a neutral atom. Atoms with more or fewer electrons are electrically charged ions.

Changing the number of neutrons in the nucleus does not change the atom's position in the periodic table but produces a new isotope whose chemical properties are generally not much different than the original isotope but whose nuclear properties can be dramatically different. The standard notation for an isotope is X^A, where X is the chemical symbol that uniquely specifies the atomic number Z. The quantity A is usually called the atomic weight but is more accurately described as the nucleon number, the number of protons and neutrons in the nucleus, where nucleon is the generic term for either a proton or a neutron.

The three types of nuclear radiation were identified: α-rays are helium nuclei, β-rays are electrons or positrons, and γ-rays are high-energy photons.

In 1932, English physicist James Chadwick confirmed the existence of the neutron. And so, as of that moment in time, the universe appeared to be reducible to just four elementary particles: the electron, the proton, and the neutron that form atoms, and the photon that composes light.

However, we have already seen that, in the same year, Anderson verified Dirac's prediction of the antielectron or positron. The implication was that a whole separate realm of matter called antimatter existed. For example, antihydrogen is comprised of an antiproton and a positron. However, antiprotons, antineutrons, and antihydrogen would not be confirmed until the 1950s.

In 1936, Anderson and his collaborator Seth Neddermeyer discovered another particle in cosmic rays that looked like an electron except it was heavier. We now call this particle the muon. It is basically a heavier electron. It would be the first of a whole new zoo of particles that would be discovered in the 1950s and 1960s.

Protons are packed close together in the nucleus and, being positively charged, strongly repel one another. So what holds the nucleus together? Because the neutron has zero charge and only a very weak magnetic field, and because gravity is so much weaker than the electric force for particles of such low mass, something else has to be holding the nucleus together. This is called the strong nuclear force since it must be strong enough to overcome the electrical repulsion between the positively charged protons in the nucleus. While the electromagnetic force acts over great distances (light reaches us from galaxies billions of light-years away), the strong nuclear force acts only between particles less than a few femtometers (10^–15 meter) apart.

Furthermore, it was discovered that the force responsible for the radioactive decay of nuclei that give β-rays (electrons) was a separate, even shorter-range force called the weak nuclear force. And it turns out that the weak force drives the primary reaction that supplies the energy of the sun and other stars.

In 1930, Pauli proposed that the missing energy that was being observed in β-decay was being carried away by a very low-mass neutral particle, which Italian physicist Enrico Fermi dubbed the neutrino. The existence of the neutrino would not be confirmed until 1956.

I will not go into the well-known story of the development of nuclear energy prior to World War II and its use in incredibly powerful bombs and as a troublesome source of energy that ultimately may be the only viable solution to the world's energy needs.

As of 1945, then, we had the proton and neutron making up nuclear matter, the electron joining these to make atomic matter, and the photon providing light. In addition, we had the positron, the muon, and the suggestion of a neutrino. These particles interacted with one another by means of four fundamental forces: (1) gravity, (2) electromagnetism, (3) the strong nuclear force, and (4) the weak nuclear force.

We also had relativistic quantum theories for photons and electrons, but these all involved only electromagnetic interactions. Dirac and others had developed a relativistic quantum field theory that could be solved only in a first-order perturbation approximation and produced infinities when pushed further. Fermi had made a start toward a theory of the weak interaction, and a Japanese physicist named Hideki Yukawa had produced a rudimentary theory of the strong interaction that did not work very well. So, a lot of problems remained.

Once the war was over, a new generation of physicists assumed command who would carry the work of the great early-century pioneers on to the next level, joining with them to leave a legacy in 1999 that, unlike 1899, successfully described all that was known at the time about the structure of matter.

Before we get to that, however, let us move back to cosmology. During the first half of the twentieth century, the ever-improving quality of telescopic observations had combined with the new physics of that period to push our view of the universe far beyond our own galaxy of stars, the Milky Way, and to provide a new picture of a universe expanding from the initial explosion called the big bang, which we will now cover.