Chapter 1
Lines and Points
Hi! I’m egghead. I will teach the following concepts in this chapter:
What is a line?
Many of the figures that you’ll see in geometry are made up of lines.
In geometry, the word line always refers to a straight line.
Technically speaking, lines go on forever. They extend into space both ways.
In geometry, this is the symbol for a line:
The arrows mean that the line goes on forever.
Naming lines
To name a line, put a letter near it. The line in this figure is line a.
What is a point?
A point is a specific location on a line.
We almost never see points by themselves in plane geometry. We usually see them on lines.
Examples
Here is a point on line p.
Here is a point on line z.
Naming points
In geometry, when we see points on a line, they usually have names.
Examples
This line has points B and C.
This line has points D, E, and F.
The points are used to show locations on the line.
Practice Questions
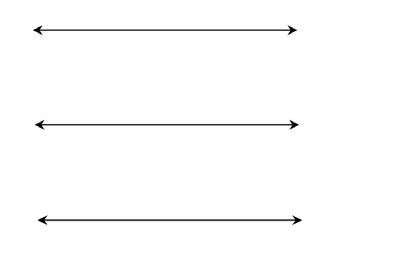
1. Name the lines shown below. Name the first line x, the second line y, and the third line z.
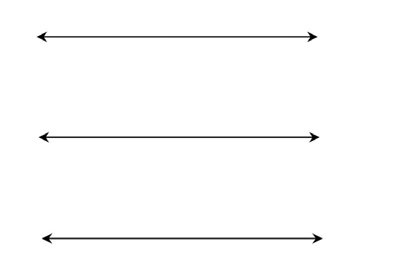
2. Name the lines shown below. Name the first line q, the second line r, and the third line s.
3. Draw in points P and Q on the line below.
4. Draw in points R and S on the line below. Name the line m.
Solutions
1.
2.
3. Points P and Q could lie anywhere on the line. In this case, point P is on the left.
4. Points R and S could lie anywhere on the line. This time, point S is on the right.
Other geometry terms: dimensions, planes, postulates, and theorems
Lines and points are two of the basic building blocks in geometry. We will talk a lot more about them in the rest of this chapter. Before we do, there are a few other concepts you should know.
Dimensions
To measure items in geometry, we refer to different dimensions, such as length, height, and width. Points are units that have no dimension. They have no size or length; they just indicate locations on a line.
Lines in geometry have one dimension. Many common shapes, such as squares and other flat figures, have two dimensions. There are also solid figures, which have three dimensions. We’ll discuss those in Part 2.
Planes
A plane is a special component of geometry that makes up a flat surface. A plane is a set of three or more points that are not on the same line. Just as lines extend infinitely both ways, planes extend infinitely in all directions. Here is a picture of how planes are usually drawn:
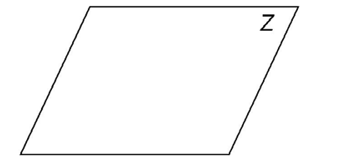
Note the capital letter Z in the upper right corner. This is the label for the plane, plane Z.
Postulates
Geometry does not just consist of shapes and figures. It also operates by certain rules. These rules define what we know about geometry and how we calculate certain measurements. Geometry postulates are statements that are accepted as true. They do not require proof, and they cannot be proven. They are taken as givens.
Theorems
A theorem is like a geometry postulate, except that it can be proven. Whereas postulates cannot be proven and are assumed to be true, theorems can be shown to be true through a series of logical steps.
One common theorem that we will discuss in a later chapter is the Pythagorean theorem. It explains the relationship between the three sides of a right triangle. Using the theorem, you can find the length of a missing side of the triangle.
Line segments
Portions of lines are sometimes called line segments. Line segment means “a part of a line.”
In this figure, the line segment starts at point B and ends at point C.
In this figure, the line segment starts at point D and ends at point E.
The figure below contains three line segments.
One line segment starts at point D and ends at point E.
Another line segment starts at point E and ends at point F.
The third line segment starts at point D and ends at point F.
Symbols
In geometry, there is a special symbol that means line segment.
Line segment BC is written as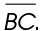 
Practice Questions
1. What is the name of the line segment below? Use the symbol for line segment.
2. What is the name of the line segment below? Use the symbol for line segment.
3. Name the line segments shown in the figure below.
Solutions
1.
2.
3. The line segments are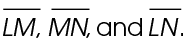 
All about length
To show the length of a line segment, we write in the measurement.
Examples
The length of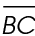 
is 4.
The length of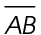 
is 10.
Finding lengths
Sometimes, lengths are not marked. We can use what we know to find the missing lengths.
Examples
In the figure below, we know that the length of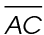 
is 5 and the length of 
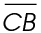is 5.
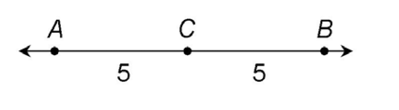
We can use what we know to find the length of 
. If 
is 5 and 
is 5, then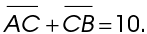 
We add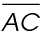 
plus 
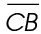to find the length of 
.
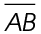We can also use subtraction to find missing lengths.
The figure shows that the length of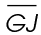 
is 13 and the length of 
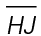is 9.
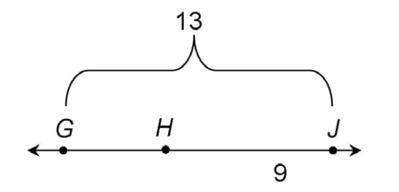
To find the length of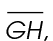 
subtract the length of 
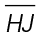from the length of 
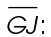13 – 9 = 4.
The length of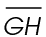 
is 4. A short way to write measurement is using the letter m.
In this case,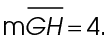 
Practice Questions
1. What is the length of line segment CD below?
2. The length of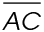 
is 6. The length of 
is 6, too. Write in the lengths on the figure below.
3. Write in the length of line segment QS in the figure below.
4. Write in the length of line segment BD in the figure below.
5. Write in the length of line segment YZ in the figure below.
Solutions
1. The length of 
is 20.
2.
3. We add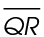 
plus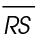 
to find the length of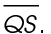 
4. We add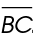 
plus 
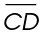to find the length of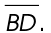 
5. The correct answer is shown below.
We subtract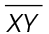 
from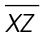 
to find the length of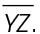 
Excellent work!
What about units?
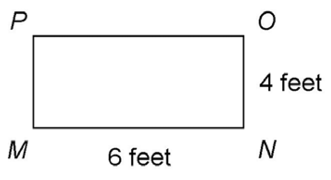
Normally, when we measure lengths, we use some sort of unit. Lengths might be in feet or inches, for example. When we use units to measure length, we simply write the unit given. For instance, the measure of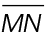 
is 6 feet.
Sometimes we must multiply the lengths of the sides of a figure. In this case, when we multiply feet by feet, the answer must be given as square feet: 6 feet × 4 feet = 24 square feet. A short way to write this is 24 ft2.
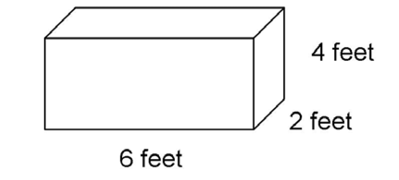
With solid figures, we might multiply three measurements. In this case, the units are expressed as cubic units. If we were to multiply 6 feet × 4 feet × 2 feet, the answer would be 48 cubic feet. We could write this in shorthand as 48 ft3.
We will work more with 2-dimensional and 3-dimensional shapes in later chapters.
Midpoints and rays
Before we leave this discussion of points and length, there is one more type of point you need to know about. This is called the midpoint.
Examples
Midpoints are points that fall halfway between two points on a line. Point Y is the midpoint of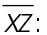 
The length of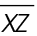 
is 8. Point Y falls in the middle of 
.
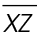Point C is the midpoint of 
.
The length of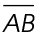 
is 10. Point C lies halfway between A and B.
Rays
A ray is section of a line that begins at one point but continues on forever. Here’s an example:
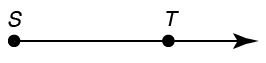
This is ray ST. It could also be written this way:
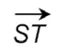
Practice Questions
1. Circle the midpoint of the line below.
2. Circle the midpoint of the line below.
3. What is the figure below?
A. Ray
B. Line
C. Line segment
4. What is the figure below?
A. Ray
B. Line
C. Line segment
5. What is the figure below?
A. Ray
B. Line
C. Line segment
Solutions
1.
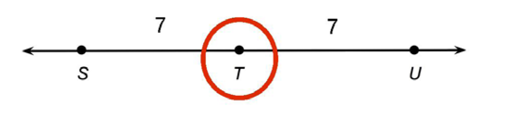
The length of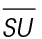 
is 14. Point T lies halfway between S and U.
2.
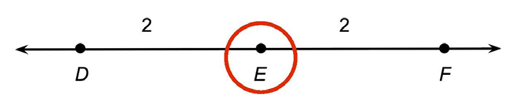
The length of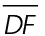 
is 4. Point E lies halfway between point D and point F.
3. The correct answer is B. The figure is a line.
4. The correct answer is C. The figure is a line segment.
5. The correct answer is A. The figure is a ray.
Parallel lines
In geometry, there are some special types of lines. The first type is called parallel.
Parallel lines are lines that don’t cross each other. They never meet.
Examples
Some parallel lines look like this:
If they have arrows on both ends, they might look like this:
Some parallel lines might have labels. The parallel lines below are labeled m and n:
Symbols
In geometry, almost every item has a symbol. The symbol for parallel lines is: ||
The parallel lines m and n in the previous example are shown with the symbol like this:
m || n
This means that line m is parallel to line n.
Sometimes, the parallel line symbol is slanted, like this: //
Either type of symbol is okay to use. You’ll probably see the || symbol most often.
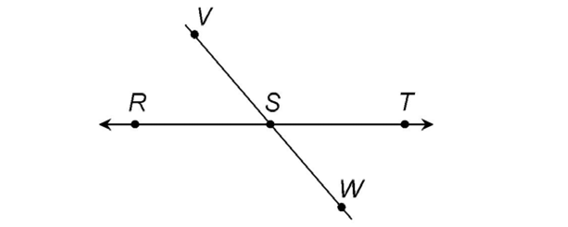
Intersecting lines
Along with parallel lines, in geometry there are also intersecting lines. Intersecting lines are lines that cross each other.
Examples
Here are some examples of what intersecting lines look like:
More examples
Here are some intersecting lines with arrows and labels:
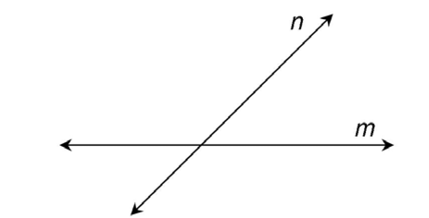
There aren’t any specific symbols to show intersecting lines. In geometry, intersecting lines are among the very few items that don’t have a symbol.
Practice Questions
1. Draw the symbol for “line a is parallel to line b.”
2. Draw line a and line b so that they are parallel.
3. Draw two lines, j and k, showing that j || k. Also show that both lines go on forever.
4. Draw lines x and y that intersect.
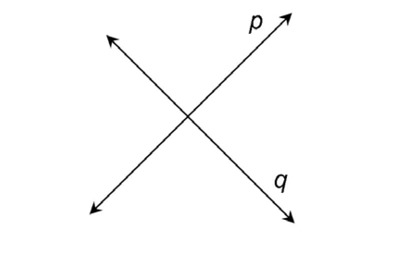
5. Draw two lines showing that line p intersects line q.
Solutions
1. The symbol is: a || b
2.
Both are correct!
3.
4.
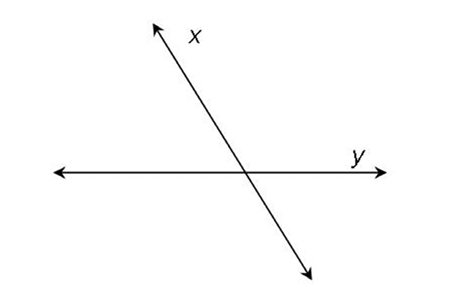
5.
Bisectors
A special type of intersecting line is called a bisector. Bisectors, or bisecting lines, are lines that cross a line segment at its midpoint. Remember midpoints? Midpoints are points that fall halfway between two points on a line. Bisectors divide a line segment into two equal parts.
Examples
In the figure shown, line m is a bisector. It divides line segment XZ into two equal parts.
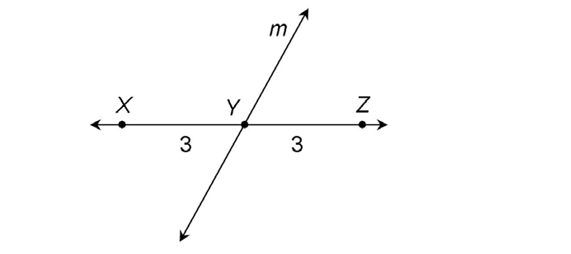
In this figure, 
bisects 
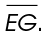As the figure shows,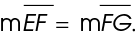 
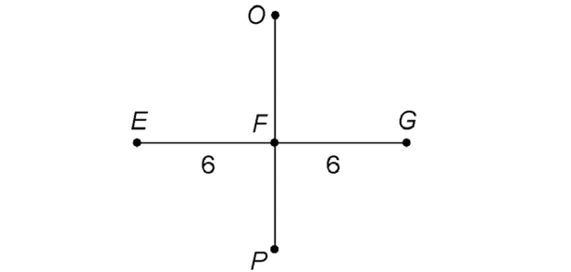
Practice Questions
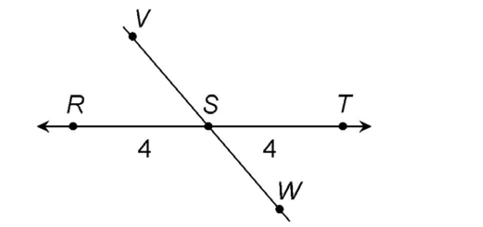
1. Line segment VW bisects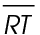 
at point S. If the measure of 
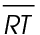is 8, what is the measure of segment RS?
2. If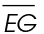 
bisects 
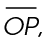what is the measure of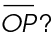 
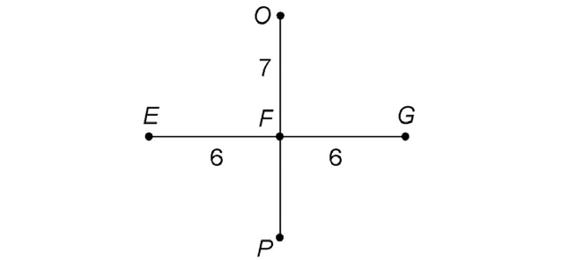
3. If line segment CD bisects line segment AB at point E, what is the measure of line segment EB?
4. Using the same figure as above, determine the measure of AB.
5. In the figure shown, line segments HI and JK are the same length. Line segment HI bisects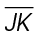 
at point L. What is the length of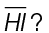 
Solutions
1. Line segment VW bisects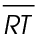 
at point S. Therefore, 
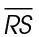and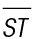 
are equal. We are told that the measure of 
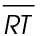is 8. Divide 
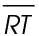into two equal parts: 8 ÷ 2 = 4.
2. We are told that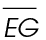 
bisects 
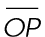. The figure shows that 
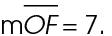Therefore, the measure of 
must also equal 7. Add together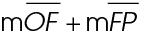 
to determine the length of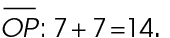 
3. Line segment CD bisects line segment AB at E. That means E is the midpoint of line segment AB, which means line segments AE and EB are equal. We are told that the measure of line segment AE is equal to 7. So the measure of line segment EB is also 7.
4. We know that both line segments AE and EB measure 7. Adding them together gives us 7 + 7 = 14. The measure of line segment AB is 14.
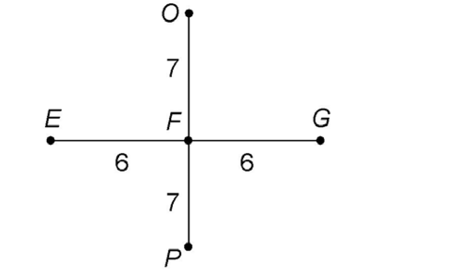
5. We are told that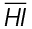 
bisects 
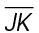. The figure shows that line segment JL equals 8, which means m
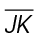= 16 (8 + 8). We’re told both line segments HI and JK are equal, so m
is 16 also.
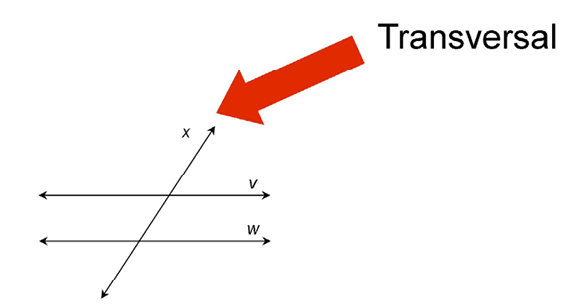
Transversals
Before we leave the subject of lines, there’s one more type of line you should know about. It’s called a transversal.
A transversal is a line that intersects two other lines.
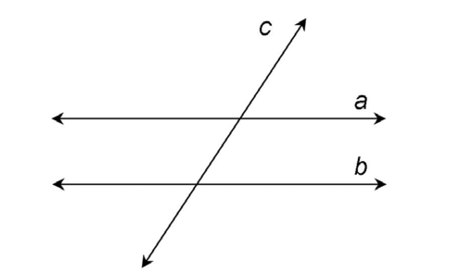
Technically, a transversal is a line that intersects two or more other lines in the same plane at different points.
What’s important is that you recognize a transversal when you see one.
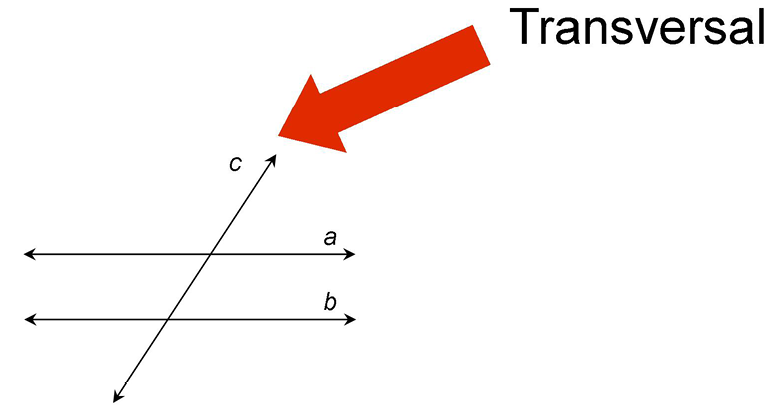
In this case, line c is a transversal. It crosses parallel lines a and b.
In geometry, we usually see transversals crossing two lines that are parallel.
Practice Questions
1. Draw a transversal, x, that intersects lines y and z. Show lines y and z as parallel.
2. Draw two parallel lines, m and n, crossed by a transversal, t.
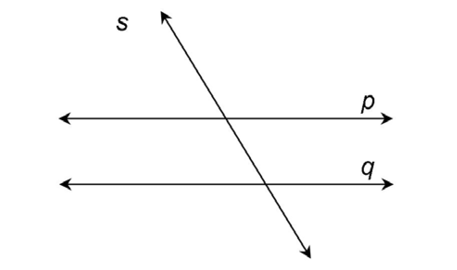
3. One more time. Draw two lines, p || q, crossed by a transversal, s.
4. Draw three parallel lines, t, u, and v, crossed by a transversal, w.
5. If a line crosses three lines that are not parallel, is it considered a transversal?
Solutions
1.
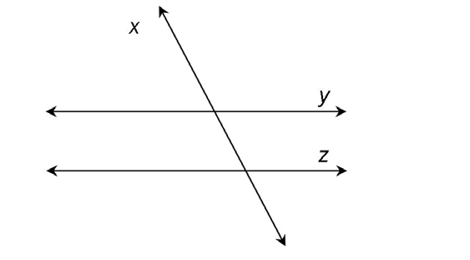
Line x could also slant the other way:
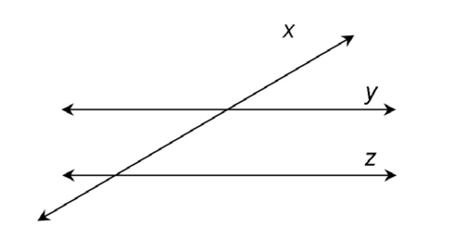
Many different options are correct.
2.
3. In this case, we have the symbol p || q. This means line p is parallel to line q. Line s is the transversal. The lines might look like this:
4. In this case, we have three lines t, u, and v that are parallel. So your drawing may look like this:
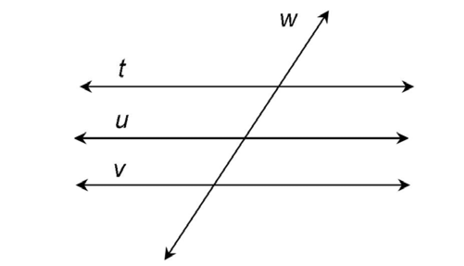
5. You were asked if a line that crosses three other lines that are not parallel is considered a transversal. The answer is yes, but only if all three lines are in the same plane, and the three lines are crossed at different points.
Chapter Review
1. Draw in points X and Y on the line below.
2. Name the line segments shown in the figure below.
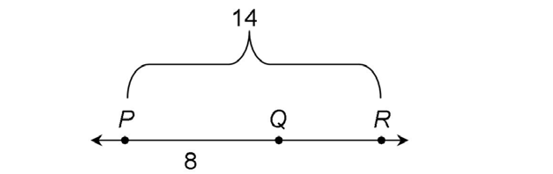
3. Write in the length of line segment JL in the figure below.
4. Write in the length of line segment QR in the figure below.
5. Circle the midpoint of the line below.
6. Draw two lines, d and e, showing that d || e.
7. Draw lines f and g that intersect.
8. In the figure shown, which line is the transversal?
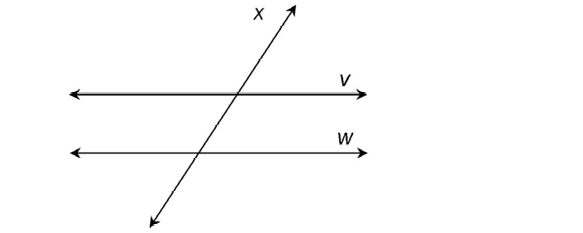
9. Draw two parallel lines, b and c, crossed by a transversal, o.
10. Draw two lines, s || t, crossed by a transversal, r.
11. Amanda lives on the same street as Harvey and Carole. Their houses lie on a straight line. Harvey’s front door is exactly 20 yards from Amanda’s front door. Carole’s front door is exactly 30 yards from Harvey’s front door. Draw a figure that shows the distances between the three houses.
12. Amanda starts at her house and walks to Harvey’s house. She stops at the door briefly to talk to Harvey, and then she continues to Carole’s house. How many yards does Amanda walk?
13. Scarlet’s school is on the same street as the library. The two buildings lie on a straight line exactly 2 miles apart. After school, Scarlet rides her bike to the library to study. When she gets to the library, she realizes she forgot her backpack in her locker, so she rides back to school, picks up her backpack, and returns to the library. How many miles does Scarlet travel in these three trips?
14. A pharmacy, a diner, and a bakery are located on the same street, shown in the figure below. The diner is on the corner of a cross street exactly 10 miles from the pharmacy. The bakery is located 20 miles from the pharmacy. What is the distance from the bakery to the diner?
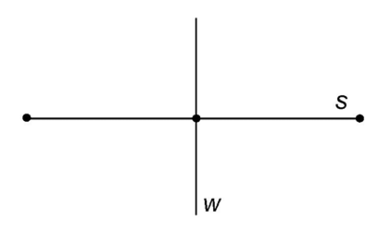
15. A wooden bar, w, bisects a steel beam, s, as shown in the figure below. If the steel beam measures 15 meters from end to end, what is the distance from one end of the steel beam to the wooden bar?
Solutions
1. Points X and Y could lie anywhere on the line.
2. The line segments are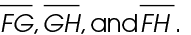 
3. We add 
plus 
to find the length of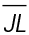 
: 3 + 6 = 9. Line segment JL measures 9 units.
4. We subtract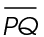 
from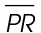 
to find the length of 
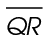. In this case, 14 – 8 = 6. Line segment QR measures 6 units.
5. The length of 
is 8. Point B lies halfway between A and C.
6.
You could also draw line e first:
7.
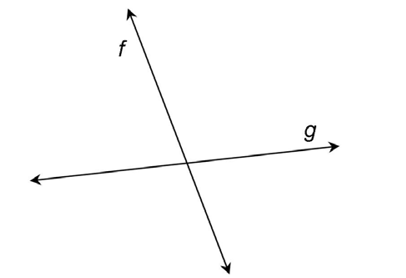
8. In this figure, line x is the transversal.
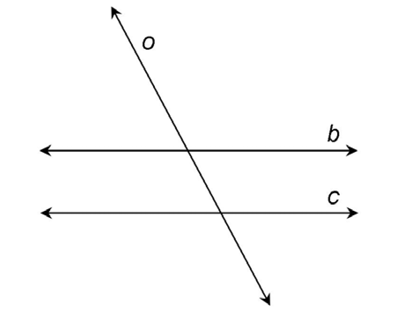
9. The lines might look like this:
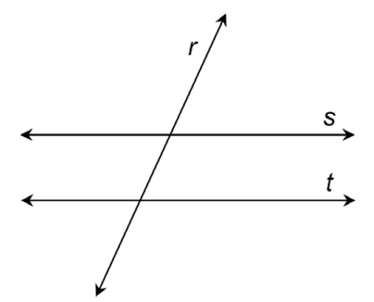
10. In this case, we have the symbol s || t. This means line s is parallel to line t. Line r is the transversal. The lines might look like this:
11. In the diagram, Amanda’s house is shown by the letter A. Harvey’s house is shown as H, and Carole’s house is labeled C.
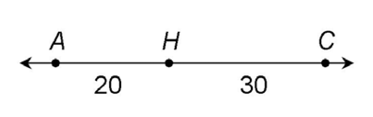
The length of line segment AH is 20; there are 20 yards between Amanda’s house and Harvey’s. The length of line segment HC is 30, as there are 30 yards between Harvey’s and Carole’s houses.
12. The correct answer is 50 yards.
Amanda starts at her house, stops at Harvey’s, and then continues to Carole’s. So, she walks 20 yards + 30 yards, or 50 yards total.
13. The correct answer is 6 miles.
The figure shows the distance from Scarlet’s school, S, to the library, L. Scarlet rides once from school to the library, then from the library to school, and a second time from school back to the library. Each time she makes the trip, she rides for two miles. The arrows in the figure show Scarlet’s three trips:
Scarlet travels 2 + 2 + 2 miles, or 6 miles total.
14. Use subtraction to determine the distance from the bakery to the diner. If the bakery is 20 miles from the pharmacy, and the diner is 10 miles from the pharmacy, this means the diner lies halfway between the bakery and the pharmacy. The diner is 20 – 10 = 10 miles from the bakery.
15. The correct answer is 7.5 meters.
The steel beam measures 15 meters total. The wooden bar bisects the steel beam, crossing the steel beam exactly in the middle. The wooden bar lies halfway between the ends of the steel beam, or 7.5 meters from each end.