Chapter 12
Cylinders
Hi! I’m egghead. I will teach the following concepts in this chapter:

What is a cylinder?
Along with cubes and rectangular solids, another three-dimensional shape is the cylinder.
A cylinder is a solid figure made up of two equal bases joined by a curved side. The bases are usually circles.
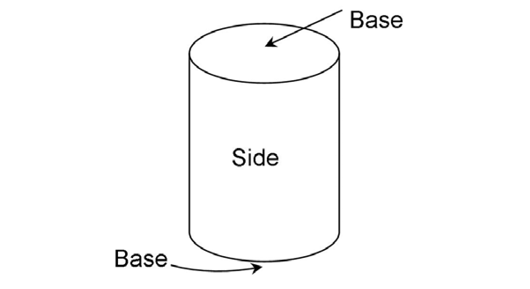
Dimensions
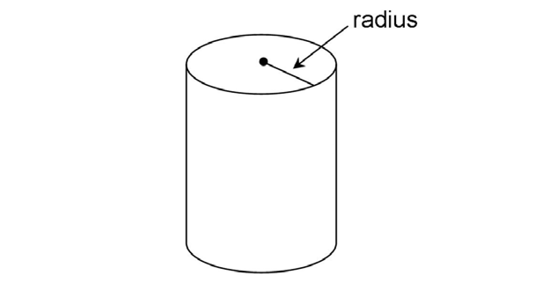
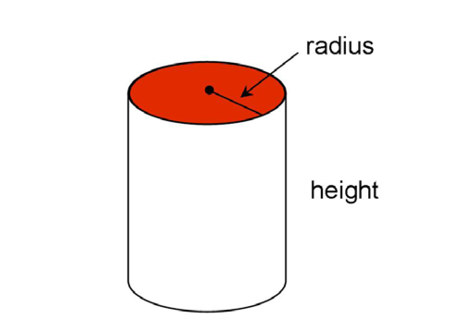
First, circular cylinders have a radius. The radius of a cylinder is the distance from the center of the figure to its edge. It is usually shown drawn on the base of the cylinder.
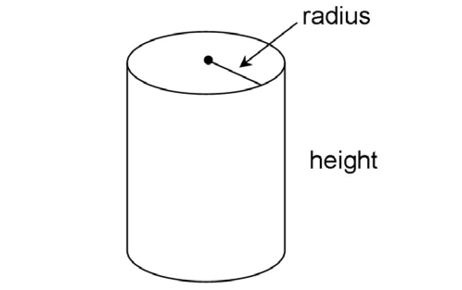
Second, cylinders also have a height measure:

Examples
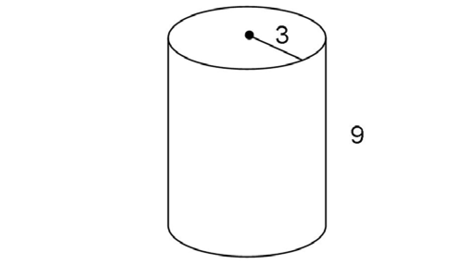
This is a cylinder with radius 3 and height 9:
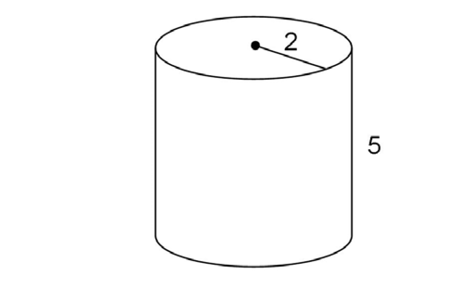
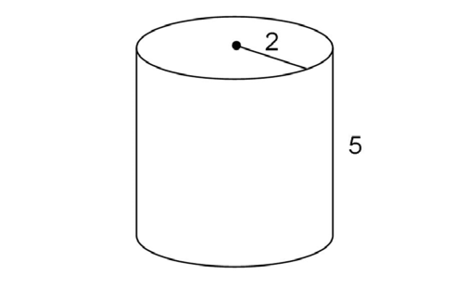
This is a cylinder with radius 2 and height 5:
Volume

The volume is the amount of space that the cylinder takes up, or the amount that it can hold.
To find the volume of a cylinder, multiply the area of the base times the height.

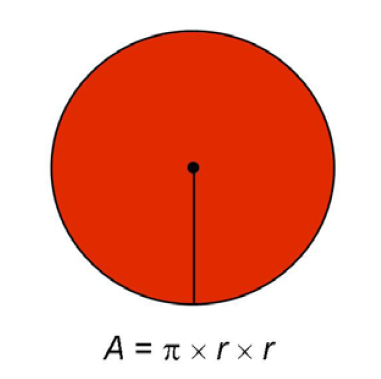
Remember how to find the area of a circle? We multiply that by the height of the cylinder.

In shorthand, it’s written like this:

Examples
To find the volume of this cylinder, we multiply the area of the base times the height.
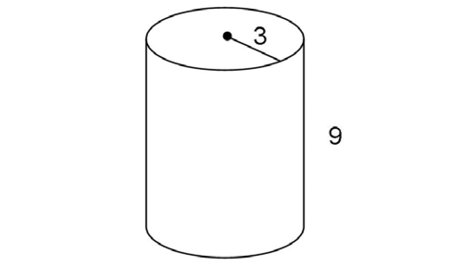
The cylinder has a radius of 3 and a height of 9. Volume =  r2h:
r2h:
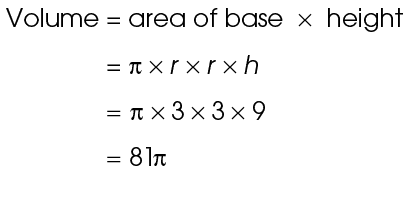
The volume of the cylinder is 81 cubic units.
cubic units.
This cylinder has a radius of 2 and a height of 5. Multiply  × r × r × h:
× r × r × h:
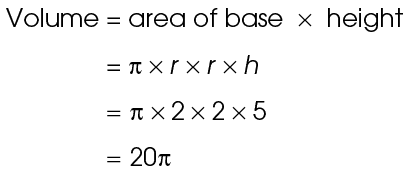
The volume of this cylinder is 20 cubic units.
cubic units.
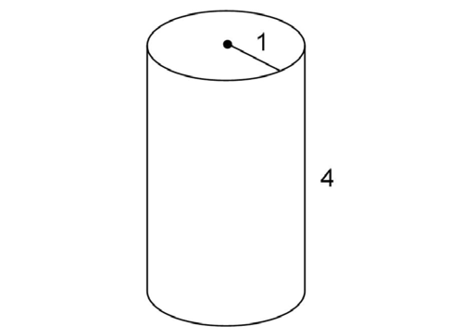
This cylinder has a radius of 1 and a height of 4.

The volume of the cylinder is 4 cubic units.
cubic units.
Practice Questions
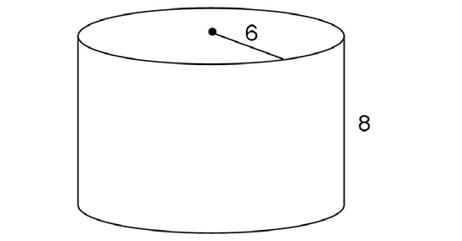
1. Find the volume of the cylinder shown.
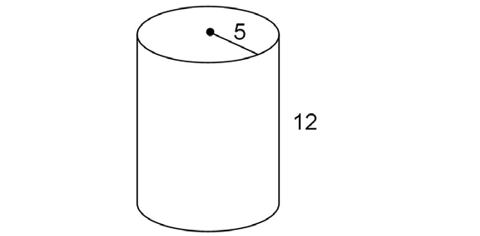
2. Find the volume of the cylinder shown.
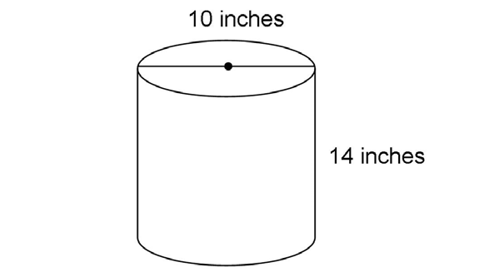
3. The cylinder shown has a diameter of 10 inches and a height of 14 inches. What is its volume?
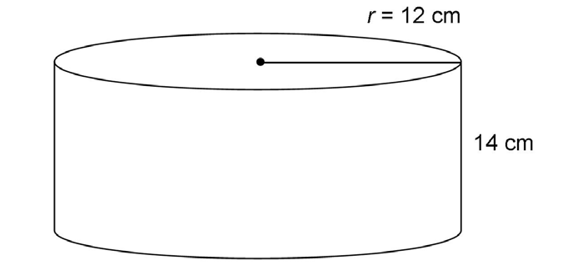
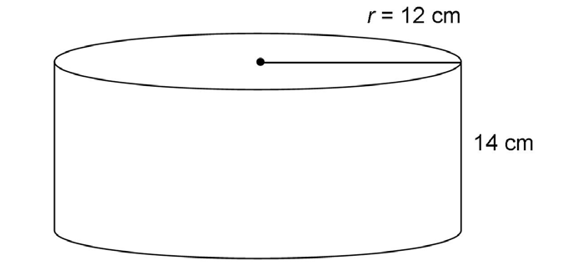
4. If a cylinder has a radius of 12 centimeters and a height of 14 centimeters, what is its volume?
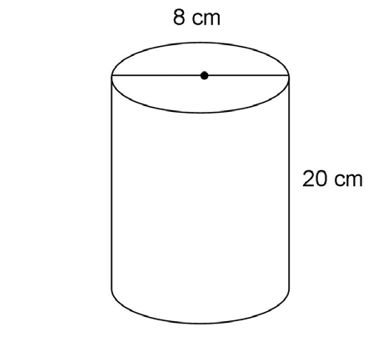
5. If a cylinder has a diameter of 8 centimeters and a height of 20 centimeters, what is its volume?
 Solutions
Solutions
1. To find the volume, we multiply  × r × r × h:
× r × r × h:

The volume is 288 cubic units.
cubic units.
2. The volume is 300 cubic units.
cubic units.

3. The volume of the cylinder is 350 cubic inches.
cubic inches.

The diameter of the cylinder is 10 inches, so its radius is 5 inches. Substitute 5 for r and 14 for h into the volume formula:

4. The volume of the cylinder is 2,016 cubic centimeters.
cubic centimeters.

5. The volume of the cylinder is 320 cubic centimeters.
cubic centimeters.
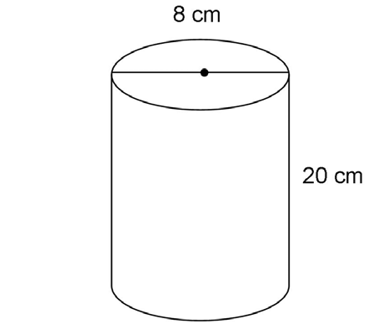
Again, we can find the radius by dividing the diameter by 2. The diameter of the cylinder is 8 centimeters, so its radius is 4 centimeters.
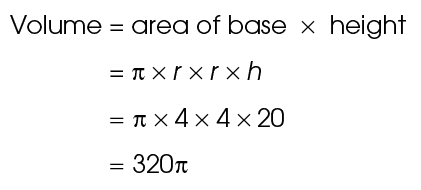
Measuring surface area
As with cubes and rectangular solids, we can also measure the surface area of cylinders.
The surface area is the area covered by the surfaces of the cylinder.

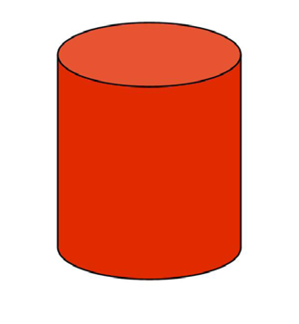
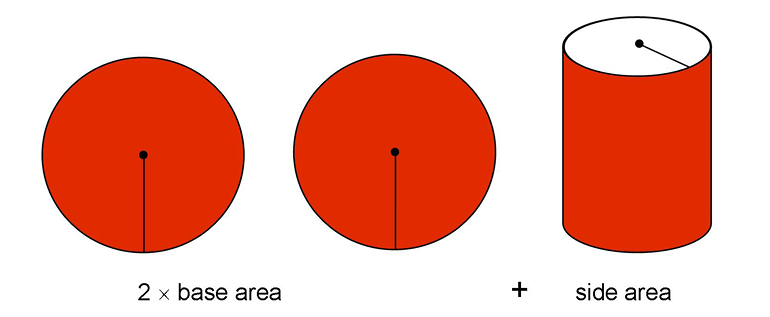
To measure the surface area, we first take the area of the base:
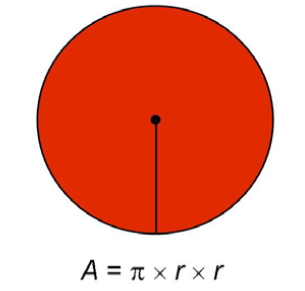
Then we multiply that by two.
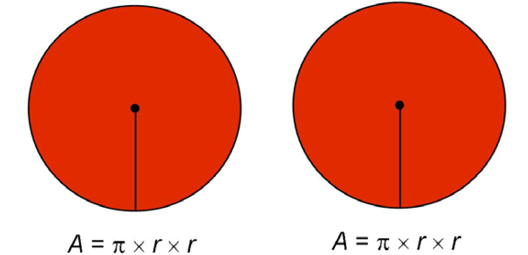
Then we add the area of the curved side:
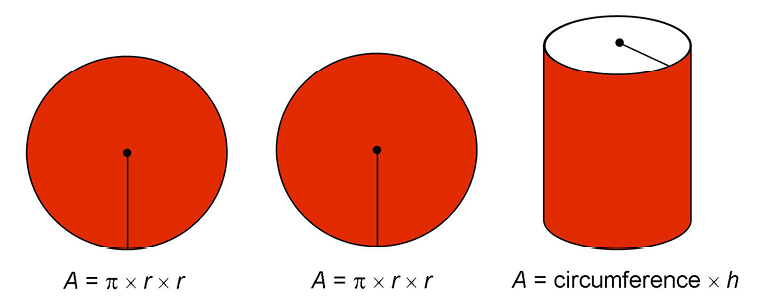
To find the area of the curved side, we first need to know its circumference. To find the circumference, we use the formula C = 2 r. Since a cylinder has two circular bases, we can use the radius of the base to calculate the circumference of the curved side.
r. Since a cylinder has two circular bases, we can use the radius of the base to calculate the circumference of the curved side.
Then we multiply the circumference times the height of the cylinder to get the area of the curved side.
Here is what it looks like very simply:
This is how you would write the formula:

Let’s shorten that up a bit:
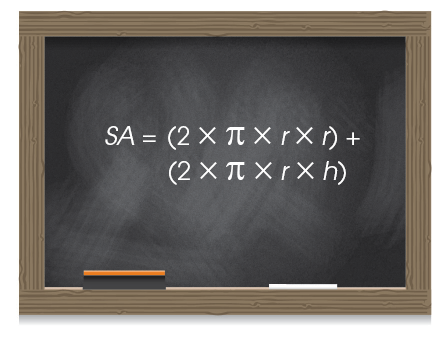

It can also be written super fancy, like this:

Don’t let the fancy expression scare you.
That just means 2 ×  × r × r plus 2 ×
× r × r plus 2 ×  × r × h!
× r × h!
Examples
Now that we’ve got the formula, let’s put it to work.
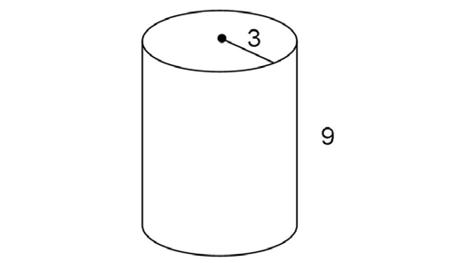
This cylinder has a radius of 3 and a height of 9. Use the surface area formula:
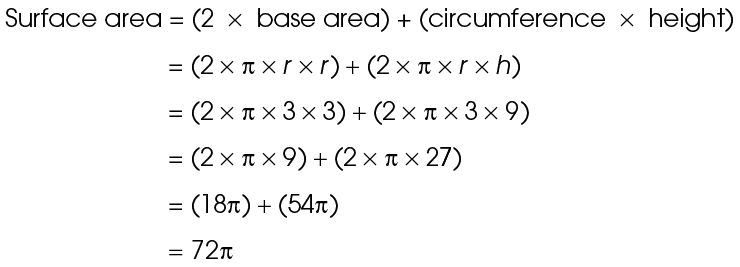
The surface area is 72 square units.
square units.
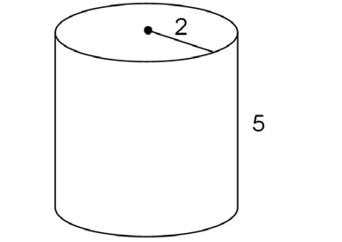
This cylinder has a radius of 2 and a height of 5. Use the surface area formula:
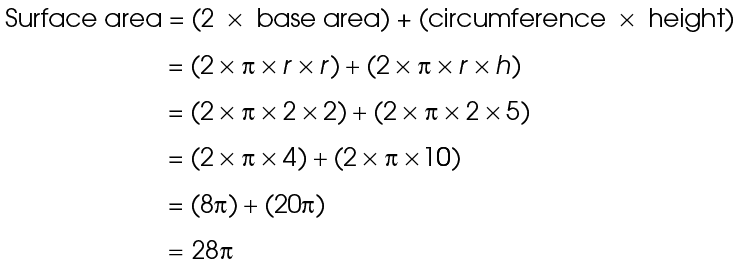
The surface area is 28 square units.
square units.
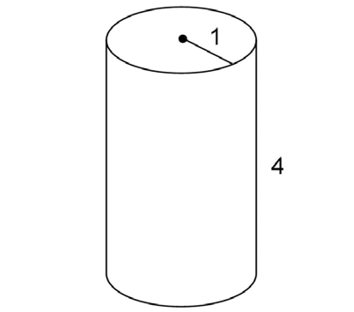
This cylinder has a radius of 1 and a height of 4. Use the surface area formula:
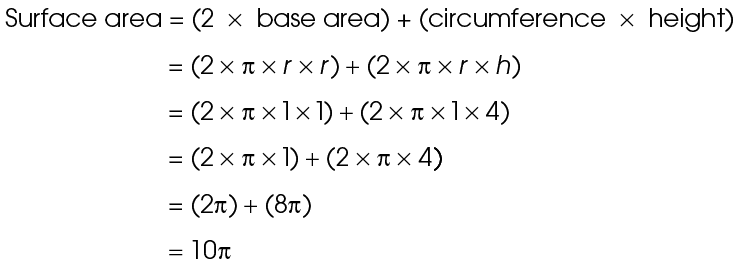
The surface area is 10 square units.
square units.
Practice Questions
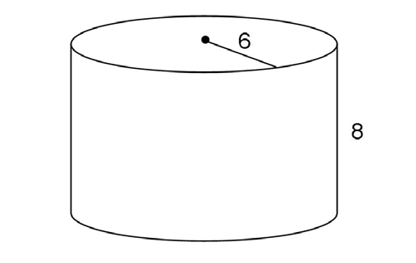
1. What is the surface area of the cylinder shown?
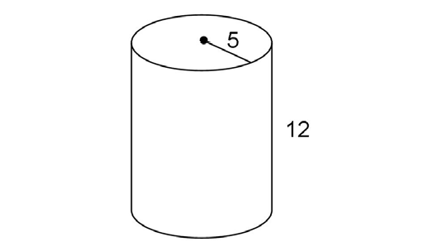
2. What is the surface area of the cylinder shown?
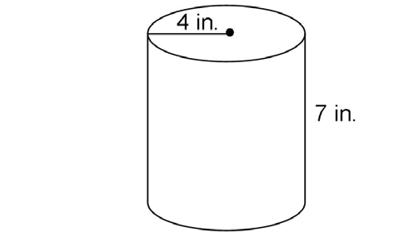
3. What is the surface area of a cylinder with a radius of 4 inches and a height of 7 inches?
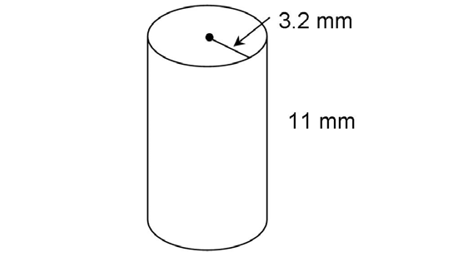
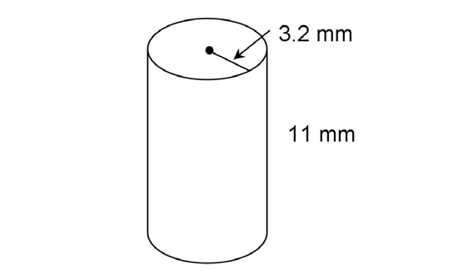
4. The cylinder shown has a radius of 3.2 millimeters and a height of 11 millimeters. Find its surface area.
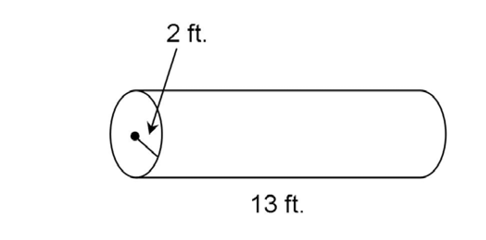
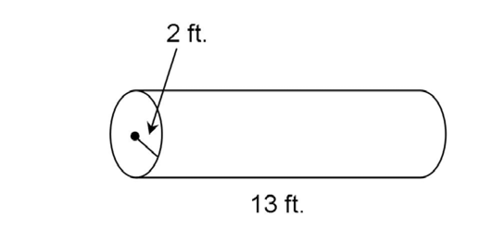
5. The cylinder shown has a radius of 2 feet and a height of 13 feet. What is its surface area?
 Solutions
Solutions
1. This cylinder has a radius of 6 and a height of 8. Use the surface area formula:
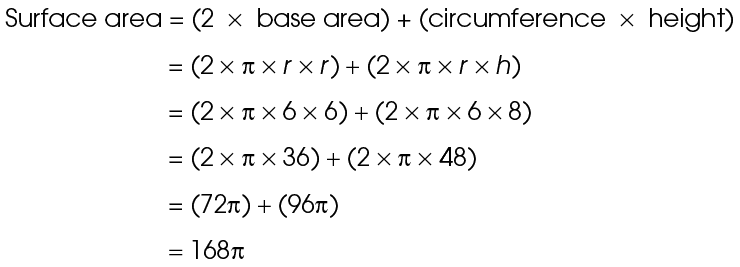
The surface area is 168 square units.
square units.
2. This cylinder has a radius of 5 and a height of 12. Use the surface area formula:
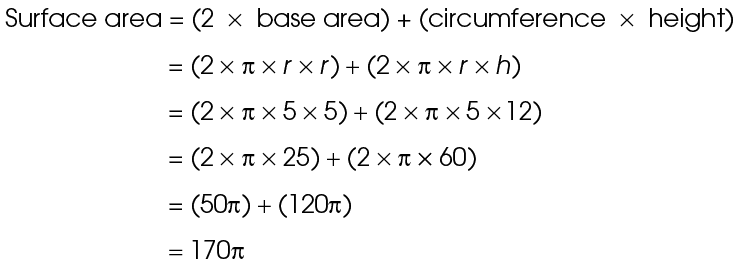
The surface area is 170 square units.
square units.
3. The surface area of the cylinder is 88 inches2.
inches2.

The radius of the cylinder is 4 inches, and its height is 7 inches. Plug these into the formula:
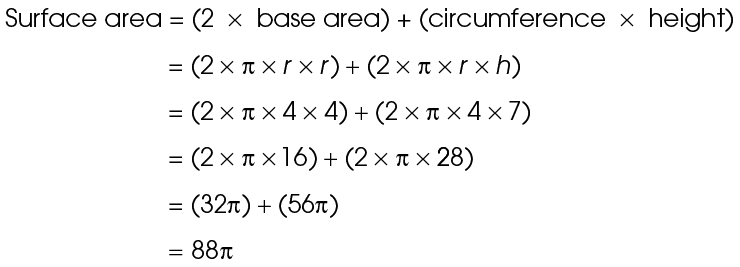
4. The surface area of the cylinder is 90.88 square millimeters.
square millimeters.

5. The surface area of the cylinder is 60 square feet.
square feet.
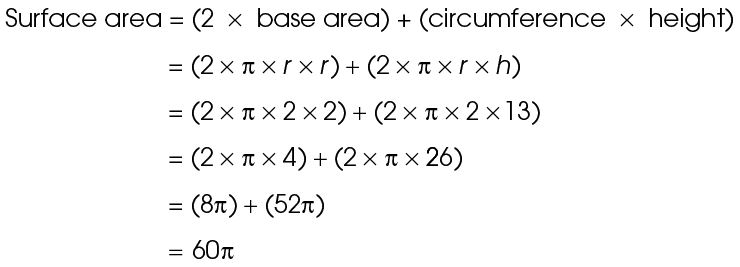
Chapter Review
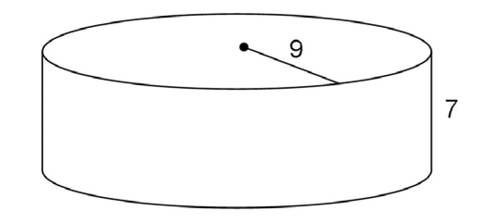
1. Find the volume of the cylinder shown.
2. What is the volume of the cylinder shown?
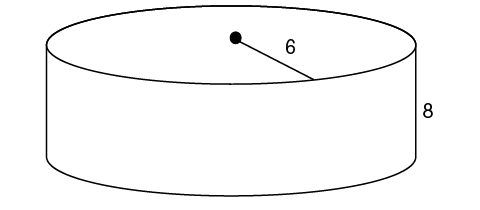
3. What is the volume of the cylinder shown?
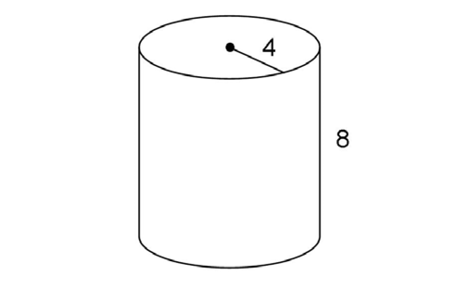
4. Find the surface area of the cylinder shown.
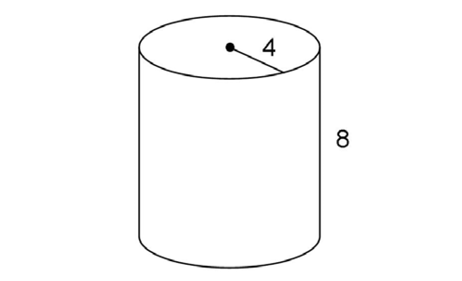
5. Find the volume and surface area of the cylinder shown.
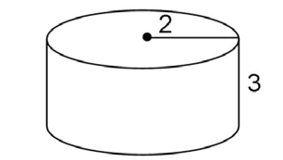
6. What is the volume of the cylinder shown?
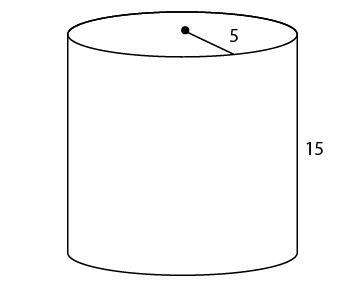
7. A grain silo has a radius of 3 meters, as shown. If the silo holds exactly 54 cubic meters of grain, how tall is the silo?
cubic meters of grain, how tall is the silo?
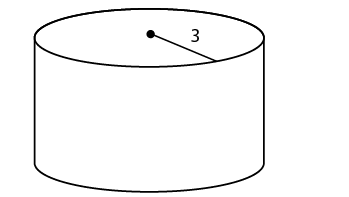
8. Find the surface area of the cylinder shown.
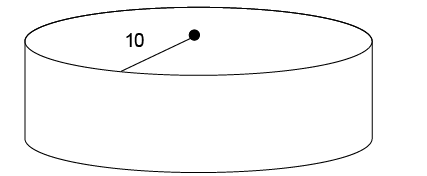
9. Bales Auto Shop stores its spare parts in a cylindrical drum that measures 10 feet from the center of the top of the drum to its outer edge, as shown. The drum has a surface area of 360 square feet. How tall is the drum?
square feet. How tall is the drum?
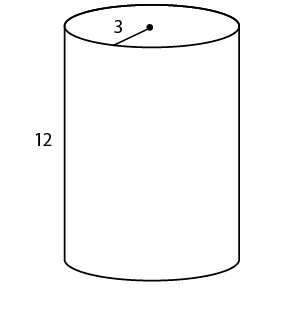
10. The cylinder shown in the figure has a diameter of 12 centimeters and a height of 18 centimeters. Find the volume and surface area of the cylinder.
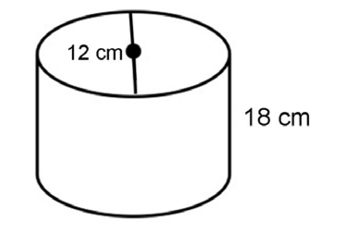
11. Joshua has a metal canister in the shape of a cylinder. Its radius is 7 inches, and its height is 21 inches. Joshua wants to wrap the canister in aluminum foil. How much foil will he need to cover the entire canister?
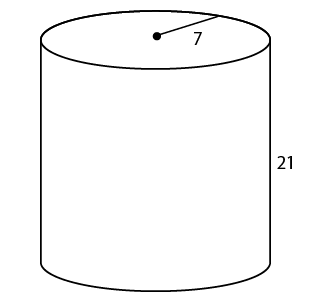
12. What is the surface area of the cylinder shown?
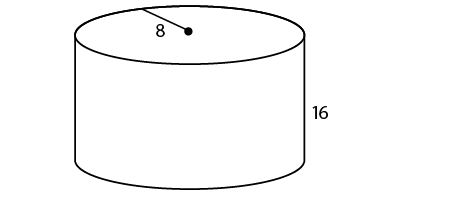
13. A water tank in the shape of a cylinder has a radius of 3.5 yards and a height of 10 yards. How much water, in cubic yards, can the water tank hold?
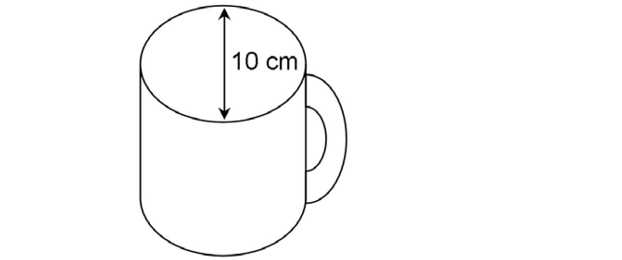
14. A coffee mug measures 10 centimeters in diameter from inside edge to inside edge. If the mug holds 275 cubic centimeters of coffee, what is the height of the mug?
cubic centimeters of coffee, what is the height of the mug?
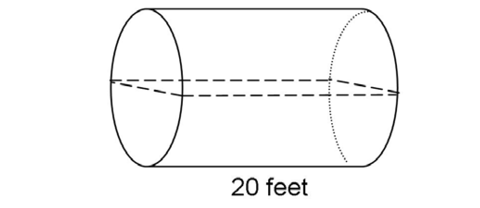
15. A concrete pipe measures 20 feet in length. The pipe is filled exactly halfway with water, as shown by the dotted lines. If the volume of water in the pipe is 160π cubic feet, find the pipe’s diameter.
 Solutions
Solutions
1. To find the volume, we multiply  × r × r × h. For this cylinder, the radius is 9 and the height is 7.
× r × r × h. For this cylinder, the radius is 9 and the height is 7.

The volume is 567 cubic units.
cubic units.
2. For this cylinder, the radius is 6 and the height is 8. Multiply  × r × r × h:
× r × r × h:
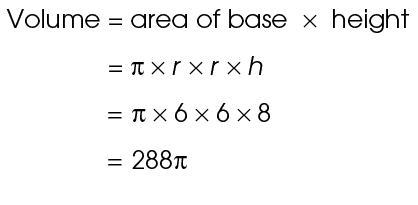

3. To find the volume, we multiply  × r × r × h. For this cylinder, the radius is 4 and the height is 8.
× r × r × h. For this cylinder, the radius is 4 and the height is 8.

The volume is 128 cubic units.
cubic units.
4. This cylinder has a radius of 4 and a height of 8. Use the surface area formula:

The surface area is 96 square units.
square units.
5.
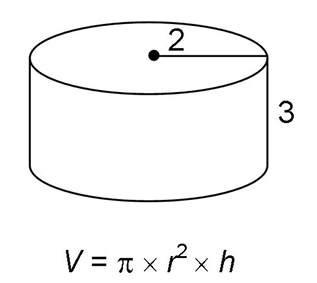
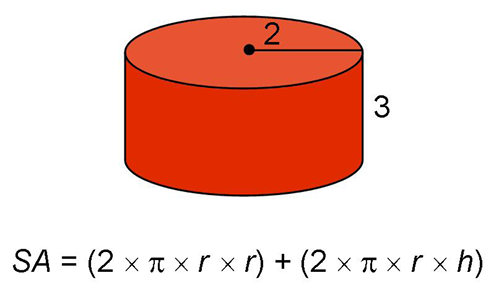
For this cylinder, the radius is 2 and the height is 3. To find the volume, multiply  × r × r × h:
× r × r × h:
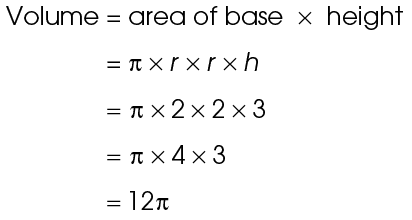
The volume is 12 cubic units.
cubic units.
To find the surface area, use the surface area formula:
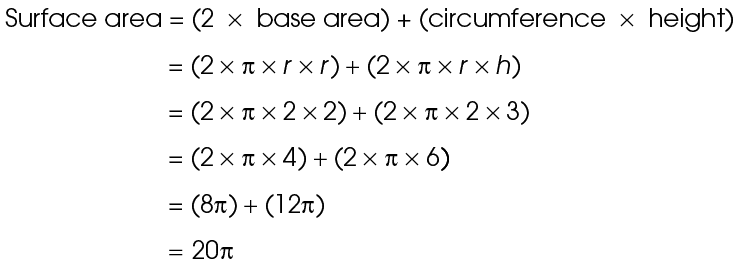
The surface area is 20 square units.
square units.
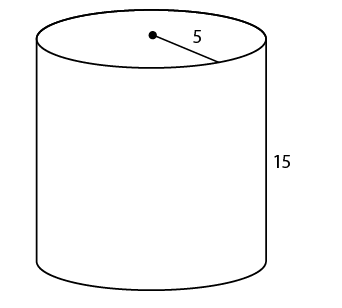
6. The volume is 375 .
.
The radius of this cylinder is 5 and the height is 15. Multiply  r2h:
r2h:
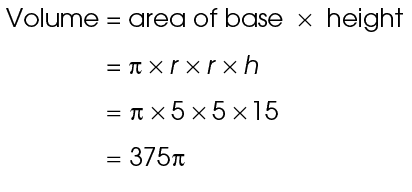
7. The height of the silo is 6 meters.
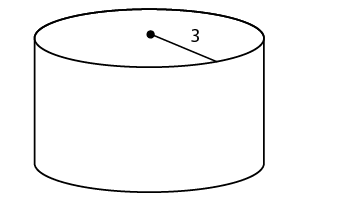
In this question, we are given the radius and volume of the silo and asked to find its height. Start with the volume formula and plug in the values given:
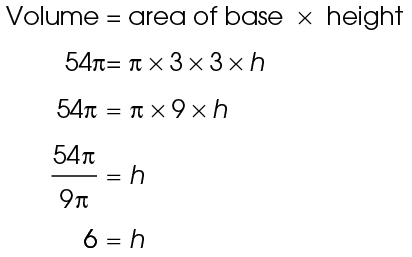
8. The surface area is 90 square units.
square units.
This cylinder has a radius of 3 and a height of 12. Use the surface area formula:
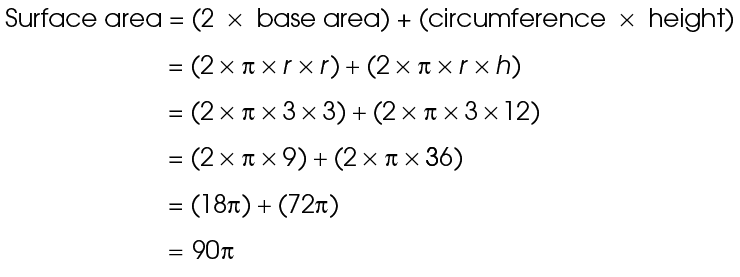
9. The drum is 8 feet tall.
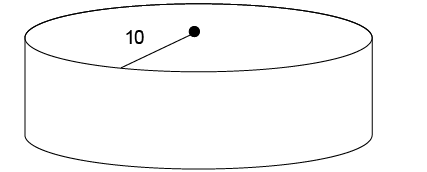
According to the question, the drum measures 10 feet from the center of its top to its outer edge. Therefore, the drum has a radius of 10 feet. Its surface area is 360 square feet. Using the surface area formula, plug in the given values and work backward to find the height:
square feet. Using the surface area formula, plug in the given values and work backward to find the height:
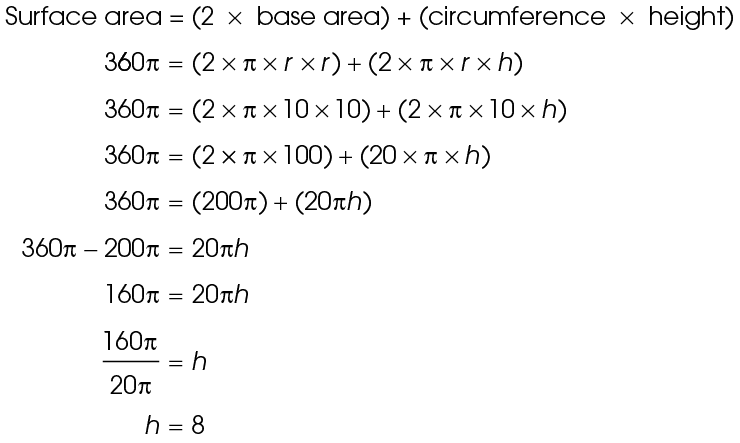
The height measures 8 feet.
10. The cylinder has a diameter of 12 centimeters. So, its radius measures 6 centimeters. To find the volume and surface area, apply the formulas as shown:

This cylinder has a height of 18 centimeters. Its volume is 648 cubic centimeters:
cubic centimeters:

Its surface area is 288 square centimeters:
square centimeters:
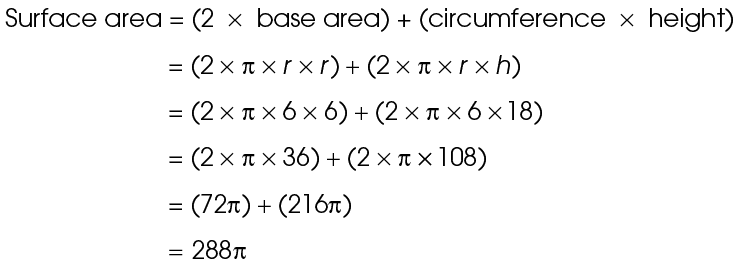
11. Joshua will need 392 square inches of foil to cover the canister.
square inches of foil to cover the canister.
This cylinder has a radius of 7 inches and a height of 21 inches. Use the surface area formula:
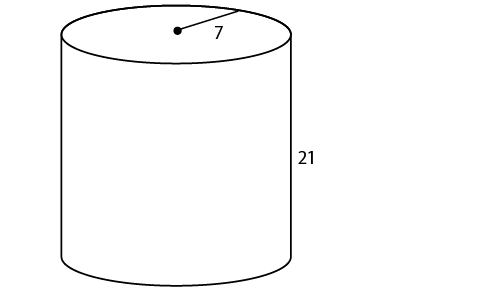
The surface area of the canister is 392 in2.
in2.
12. The surface area is 384 .
.
This cylinder has a radius of 8 and a height of 16. Use the surface area formula:
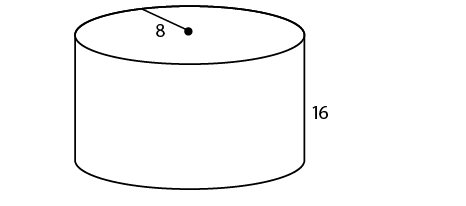
13. The tank can hold 122.5 cubic yards of water.
cubic yards of water.
To answer this question, find the volume of the tank. The tank has a radius of 3.5 yards and a height of 10 yards. Multiply  × r × r × h:
× r × r × h:
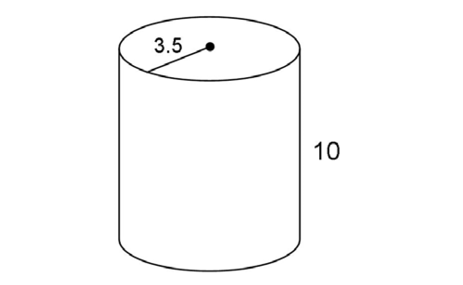

The volume of the tank is 122.5 cubic yards.
cubic yards.
14. The height of the mug is 11 centimeters.
The volume of the mug is 275 centimeters, and its diameter is 10 centimeters. This means its radius is 5 centimeters. Plug these values into the volume formula and solve for the height:
centimeters, and its diameter is 10 centimeters. This means its radius is 5 centimeters. Plug these values into the volume formula and solve for the height:
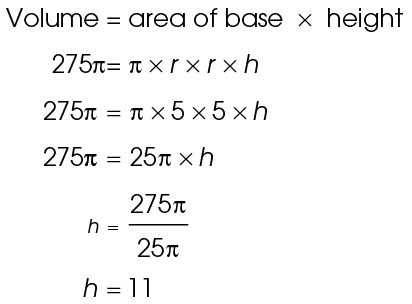
15. The diameter of the pipe is 8 feet.
When the pipe is half full, it holds 160 ft.3 of water. To find the total volume of the pipe, double this figure: the volume is 320
ft.3 of water. To find the total volume of the pipe, double this figure: the volume is 320 ft3.
ft3.
We are told that the pipe measures 20 feet in length. Using the volume formula, solve for the radius of the pipe:
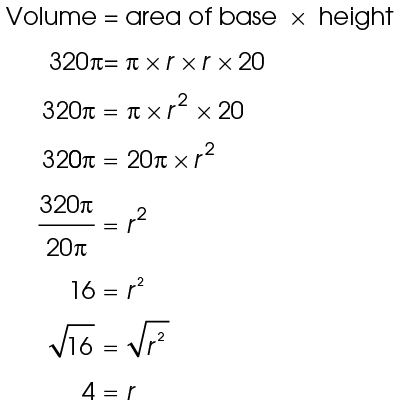
If the radius of the pipe is 4 feet, the diameter of the pipe must be 8 feet.