Chapter 4

Triangles

Hi! I’m egghead. I will teach the following concepts in this chapter:

What is a triangle?

A triangle is a shape with three sides.

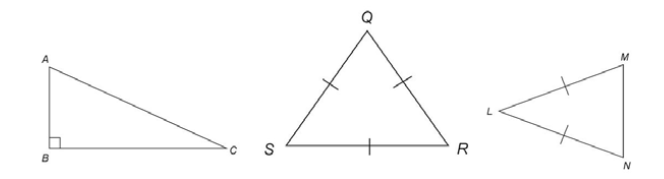
Triangles have three sides and three angles. Here are some examples:

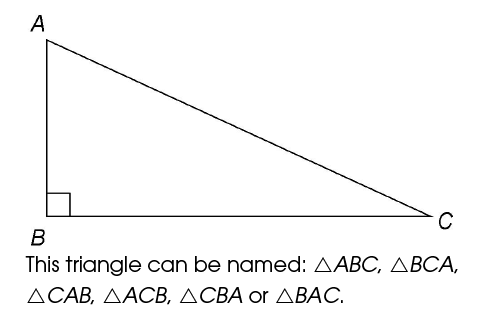
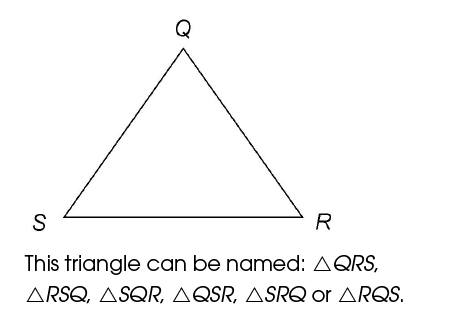
Naming and symbols

To name a triangle, use its points or vertices.

Triangles have three vertices. Each triangle therefore has three letters in its name. When naming a triangle in short form, use the symbol . You can begin at any vertex.

Interior angles

There’s one important property triangles have that is crucial to know:

The measures of the inside angles of a triangle add up to 180°.

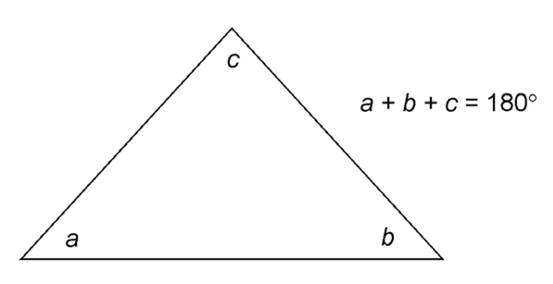
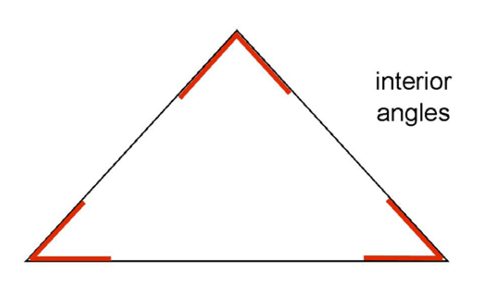
These inside angles are called interior angles.

Exterior angles

Triangles also have exterior angles. Exterior angles are formed when one side of a triangle is extended in a straight line:

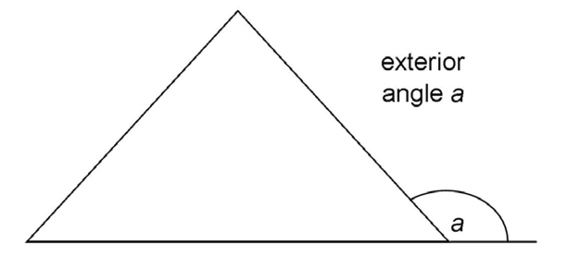
Exterior angles are supplementary to their adjacent interior angles. In the triangle shown, exterior angle a is supplementary to interior angle d. Their measures add up to 180°.

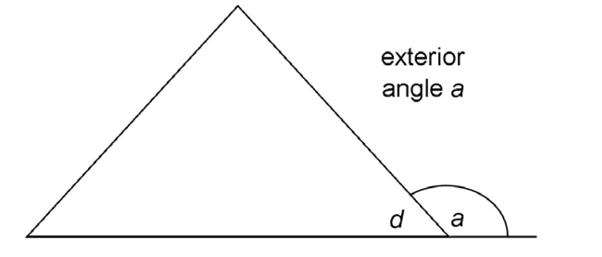
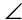The measure of each exterior angle is also equal to the sum of the two non-adjacent interior angles of the triangle. In the triangle shown, ma = mb + mc.

Types of triangles

Triangles can be classified by the size of their angles or lengths of their sides. Triangles classified by their sides include:

1. Isosceles triangles

2. Equilateral triangles

3. Scalene triangles

Triangles classified by their angles include:

1. Right triangles

2. Acute triangles

3. Obtuse triangles

Once you know the properties of triangles, it’s easy to tell them apart.

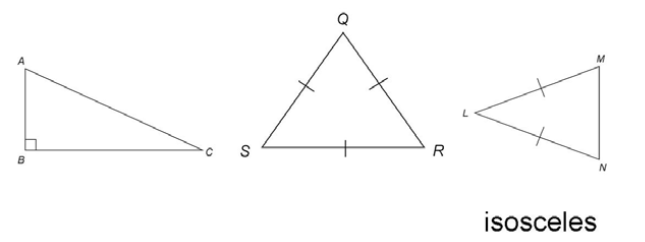
Isosceles triangles

Isosceles triangles have two equal sides.

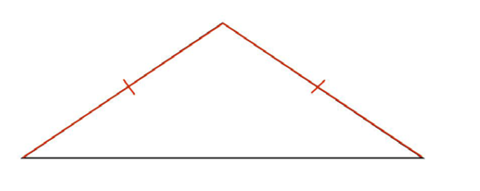
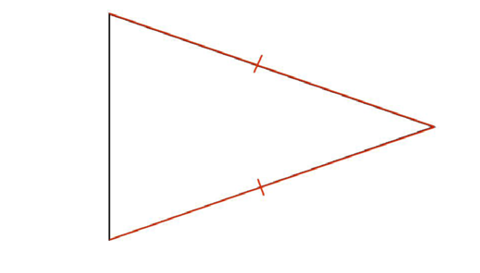
Isosceles triangles also have two equal angles:

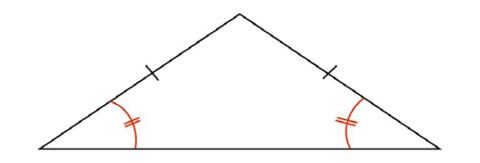
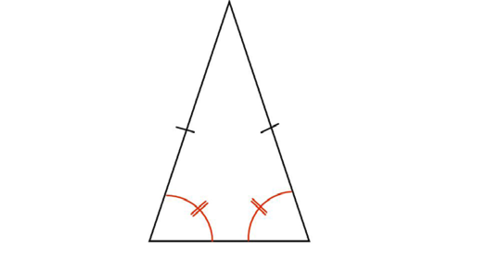
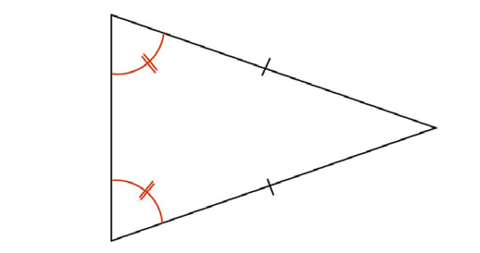
The equal angles lie across from the equal sides!

Equilateral triangles

Equilateral triangles have three equal sides.

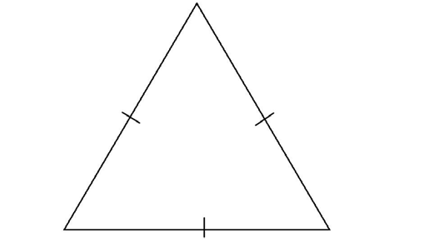
They also have three equal angles.

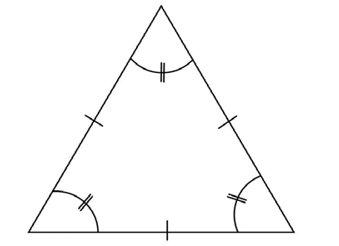
Scalene triangles

Scalene triangles are triangles that have three sides of different lengths. They have no equal angles.

Right triangles

Right triangles have one right angle.

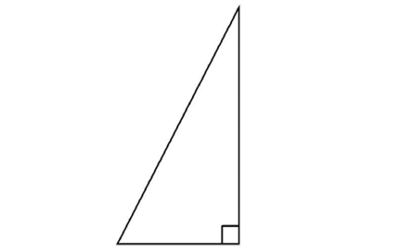
Acute triangles

An acute triangle has three angles less than 90°.

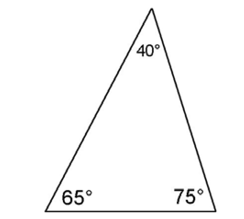
Obtuse triangles

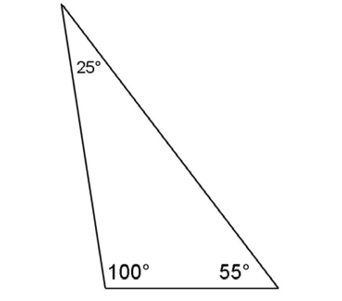
An obtuse triangle has one of its interior angles measuring more than 90°.

Practice Questions

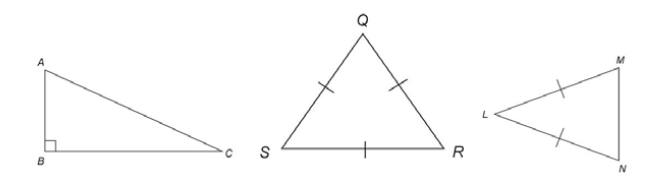
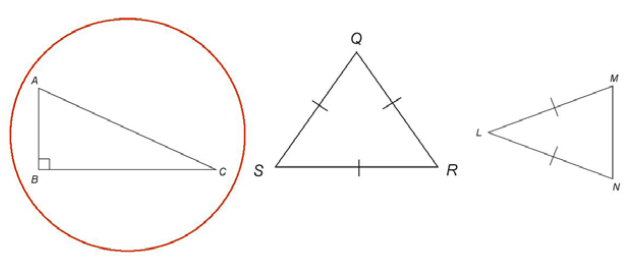
1. Which one of the triangles shown is a right triangle?

2. Which type of triangle is LMN? Write the correct name in the space below the figure.

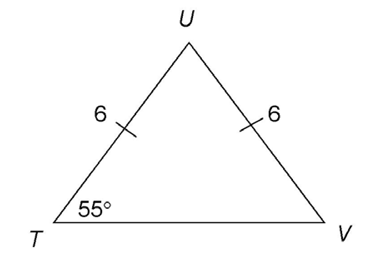
3. What is the measure of V?

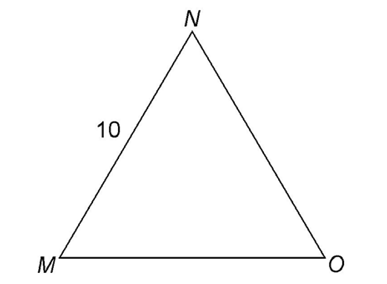
4. Triangle MNO is an equilateral triangle. What is the length of MO?

5. The triangle shown is a scalene triangle. What is the value of x?

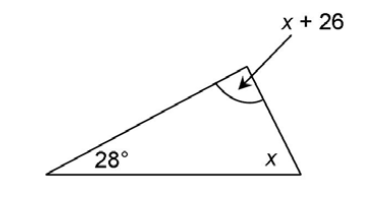
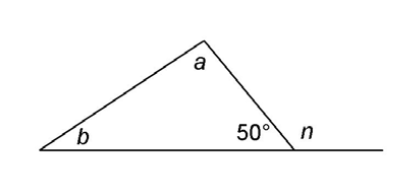
6. In the triangle shown, what is the measure of exterior angle n?

Solutions

1.

2.

3. This is an isosceles triangle. It has two equal sides and two equal angles. The equal angles lie across from the equal sides. Side TU equals side VU, so T equals 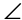V.

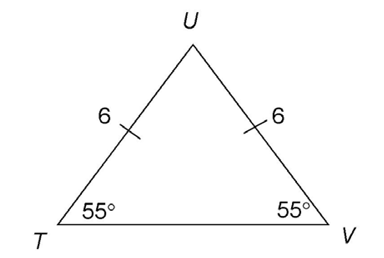
4. MNO is an equilateral triangle. All three sides are equal.

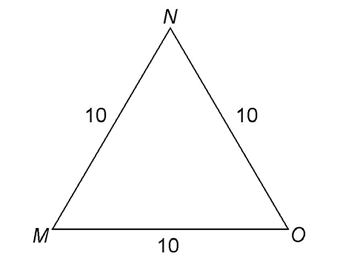
5. The value of x is 63°.

The triangle is a scalene triangle. This means no sides or angles are equal. However, we do know that the sum of the interior angles of a triangle is 180°. Set up an equation and solve for x:

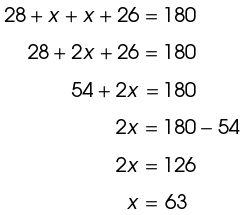
6. The measure of n is 130°.

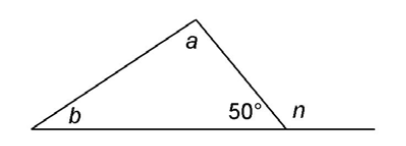
Angle n is an exterior angle, so it is supplementary to the angle that measures 50°. The measures of these two angles add up to 180°. To find the measure of angle n, use subtraction: 180° – 50° = 130°.

Finding perimeter

Now that you’ve learned the different types of triangles, let’s take a look at perimeter questions. Perimeter questions for triangles are similar to those you would see for quadrilaterals.

The perimeter of a triangle is the distance around its outside edge. The dotted arrows show the perimeter of the triangle below:

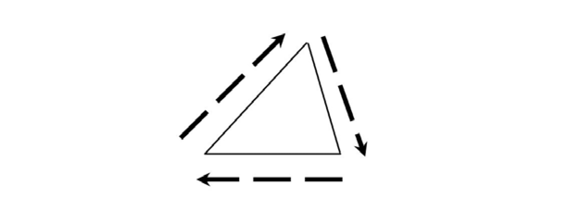
Formula

To find the perimeter, add up the lengths of the three sides:

Since we’ve already done this quite a bit with quadrilaterals, we’ll now try some more challenging questions.

Practice Questions

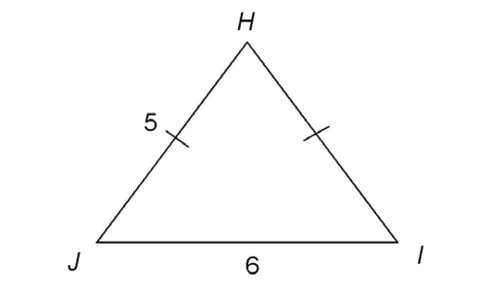
1. Triangle HIJ is isosceles. What is the perimeter of HIJ?

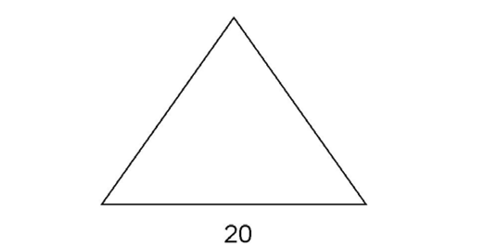
2. The figure below is an equilateral triangle. Find its perimeter.

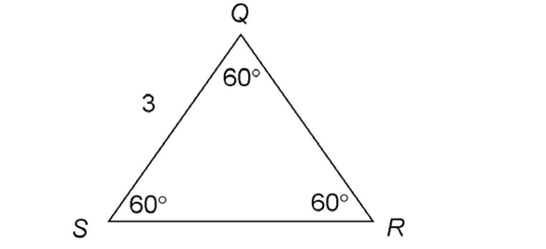
3. What is the perimeter of triangle QRS?

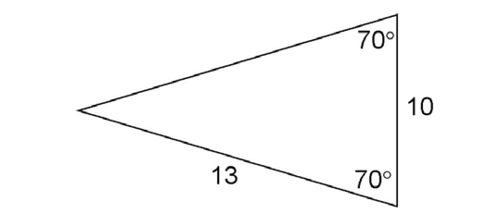
4. What is the perimeter of the triangle shown?

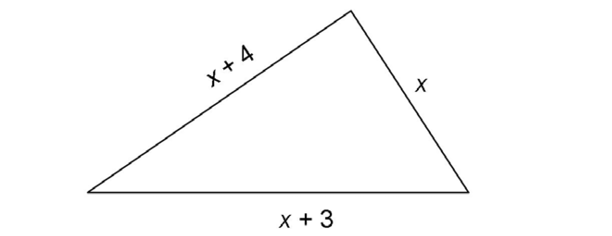
5. The triangle shown has a perimeter of 22 inches. What are the lengths of its sides?

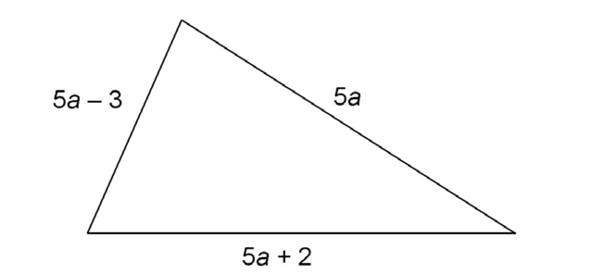
6. If the perimeter of the triangle shown is 29 centimeters, what is the value of a?

Solutions

1. An isosceles triangle has two equal sides. The figure shows that side JH is congruent to side IH. That means side IH measures 5. The perimeter is 5 + 5 + 6, or 16.

2. An equilateral triangle has three equal sides. That means all sides measure 20.

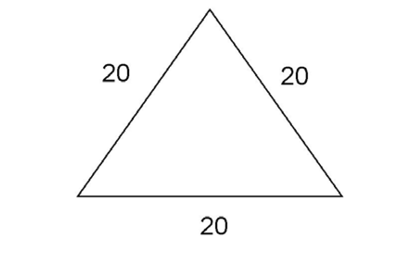
The perimeter is 20 + 20 + 20, or 60.

3. A triangle with three equal angles is an equilateral triangle. All sides are also equal.

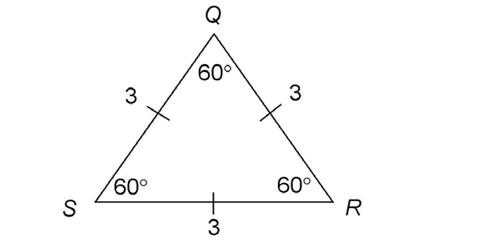
The perimeter is 3 + 3 + 3, or 9.

4. A triangle with two equal angles is an isosceles triangle. The sides opposite the equal angles are also equal. The missing side must therefore equal 13:

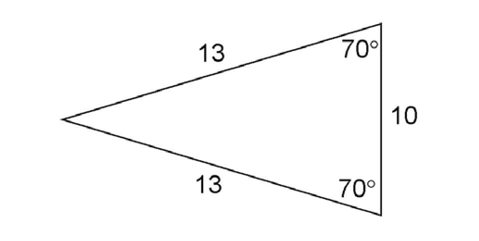
The perimeter is 13 + 13 + 10, or 36.

5. The sides of the triangle measure 5 inches, 8 inches, and 9 inches.

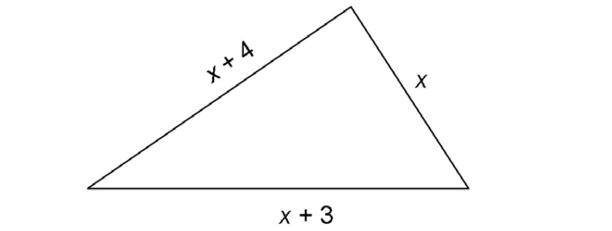
Using the perimeter formula, write an equation: x + (x + 4) + (x + 3) = 22. Solve for x:

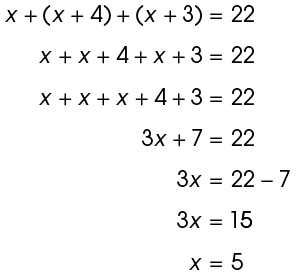
The value of x is 5. So, the lengths of the sides are 5 inches, 5 + 3 = 8 inches, and 5 + 4 = 9 inches.

6. The value of a is 2 centimeters.

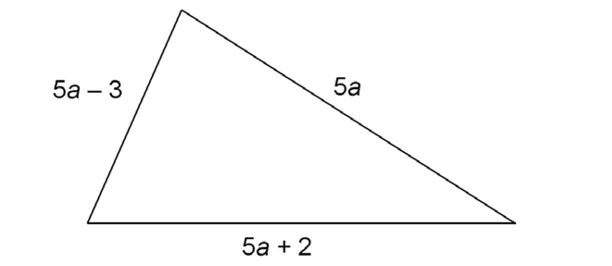
Use the perimeter formula to set up an equation: 5a + (5a – 3) + (5a + 2) = 29. Then solve for a:

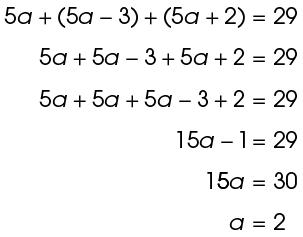
We are just asked for the value of a, not the length of the sides, so we can stop here. The value of a is 2 centimeters.

Finding area

Nice work with those more challenging perimeter questions. Often, test questions in geometry require you to find a missing length, based on what you know about the shape.

In addition to asking about perimeter, triangle questions also ask about area.

The area of a triangle is the space the triangle covers. The shaded area shows the area of the triangle below:

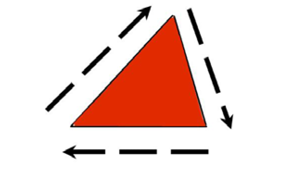
Formula

The area of a triangle equals 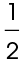of its base × height.

In shorthand, the formula looks like this:

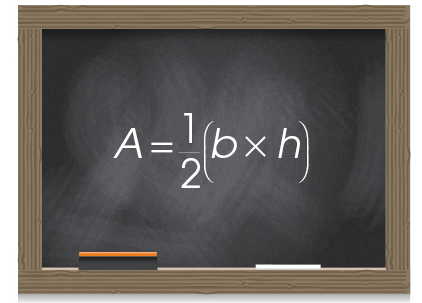
It can also be written like this:

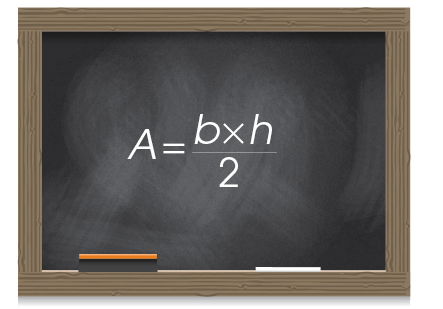
Base and height

The base and height of a right triangle are easiest to find. They are the sides next to the right angle:

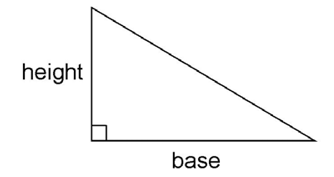
As long as you use the sides next to the right angle, and not the hypotenuse, it doesn’t matter which side you call the base and which side you call the height:

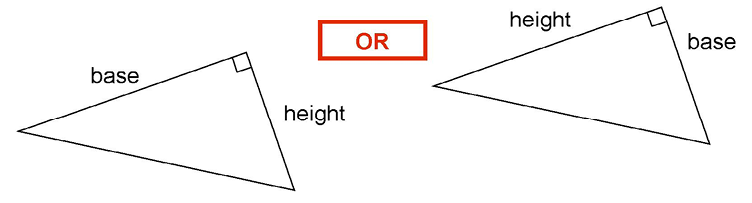
You are multiplying them, so the area still comes out the same!

Practice Questions

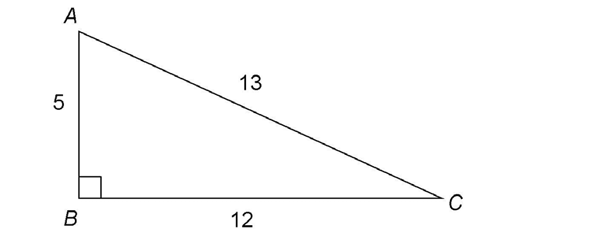
1. What is the area of ABC?

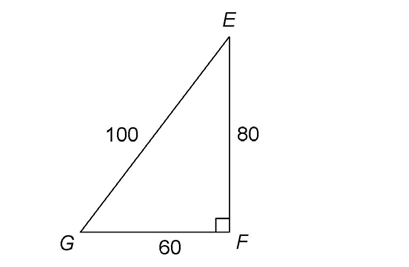
2. What is the area of EFG?

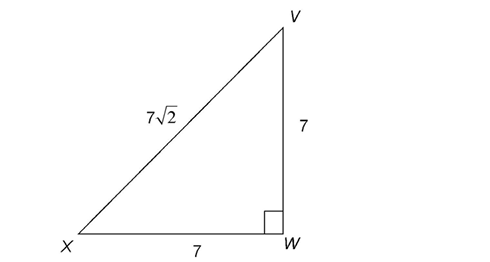
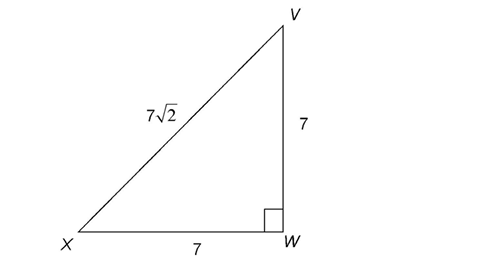
3. If VW = 7 inches and XW = 7 inches, what is the area of VWX?

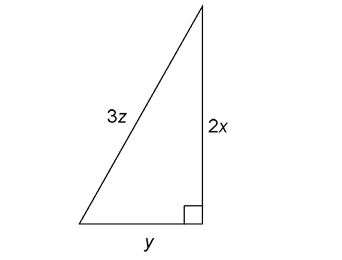
4. The triangle shown has sides measuring 2x feet, y feet, and 3z feet. What is the area of the triangle?

Solutions

1. The area is 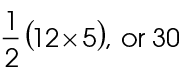square units.

2. The area is 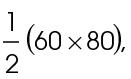or 2,400 square units.

3. The area of the triangle is 24.5 square inches.

To find the area, substitute 7 for b and 7 for h into the area formula:

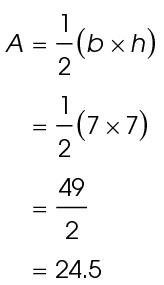
4. The area of the triangle is xy square feet.

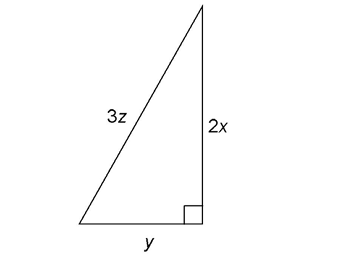
Use the area formula, 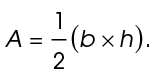For this question, you’re only given variables and not actual numbers, so substitute the variables in for the base and the height. Plug in y for the base and 2x for the height:

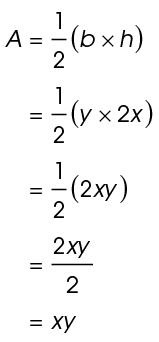
More heights

With isosceles and equilateral triangles, finding the height is a little more complex.

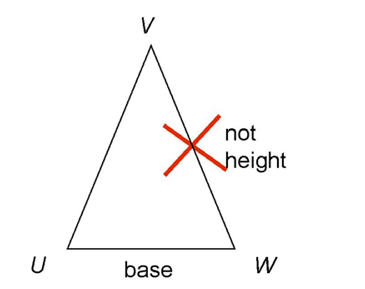
Like with parallelograms, you can use one side of the triangle as the base, but you can’t use another side of the triangle as its height:

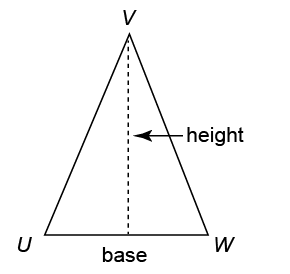
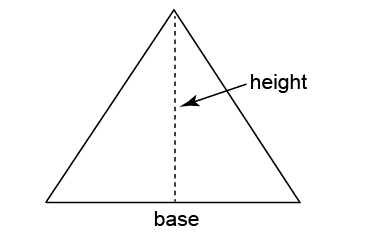
The dotted line shows the height of the triangle. Here is another example:

Practice Questions

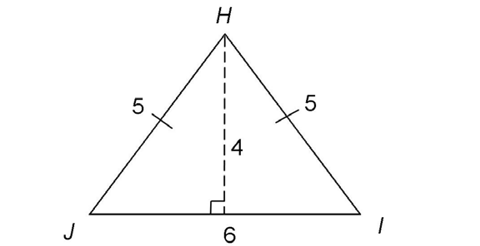
1. What is the area of triangle HIJ?

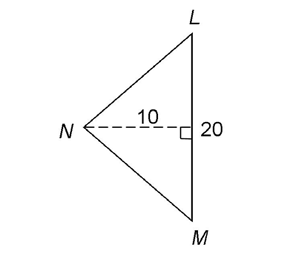
2. What is the area of LMN?

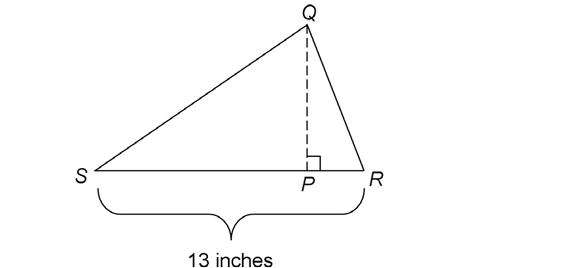
3. In QRS shown, the length of 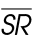is 13 inches. The area of the triangle is 52 square inches. What is the length of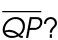

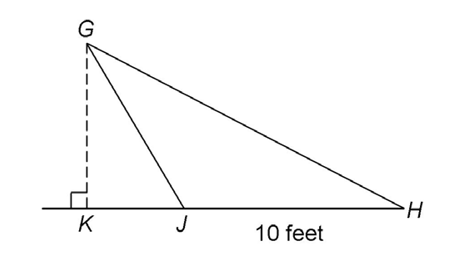
4. The area of GHJ is 47.5 square feet. What is the length of

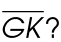
Solutions

1. The area equals 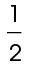of the base times the height. The dotted line shows the height, 4. The area is:

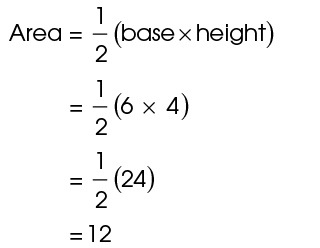
2. The base, LM, is 20. The height, shown by the dotted line, is 10. The area is:

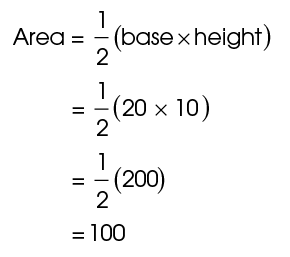
3. The length of is 8 inches.

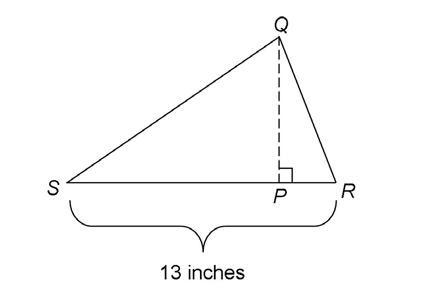
In this triangle, 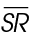represents the base, and represents the height. Using the area formula, solve for the length of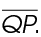

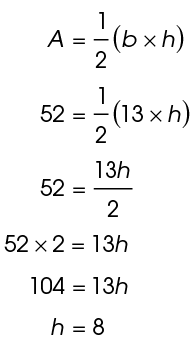
4. The length of 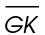is 9.5 feet. In this triangle, 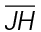represents the base, and 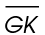represents the height. Using the area formula, solve for the length of .

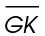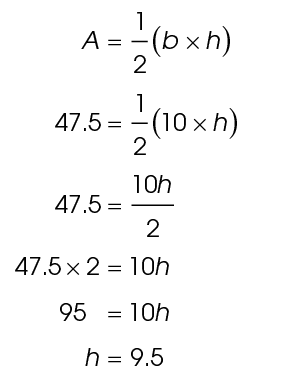
Triangle side length

When triangles are drawn, their sides must fit a certain rule. The sum of any two sides must always be greater than the length of the remaining side.

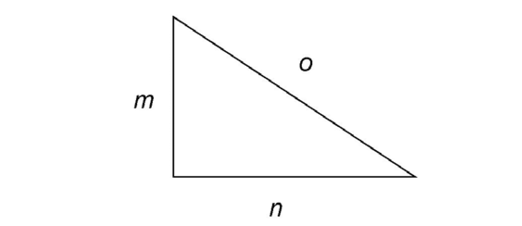
In the triangle shown, the length of m + n must be greater than the length of o. Similarly, m + o must be greater than n, and n + o must be greater than m.

Example

A triangle could have sides of length 6, 8, and 10. But it could not have sides of length 6, 8, and 20, because 6 + 8 is not greater than 20.

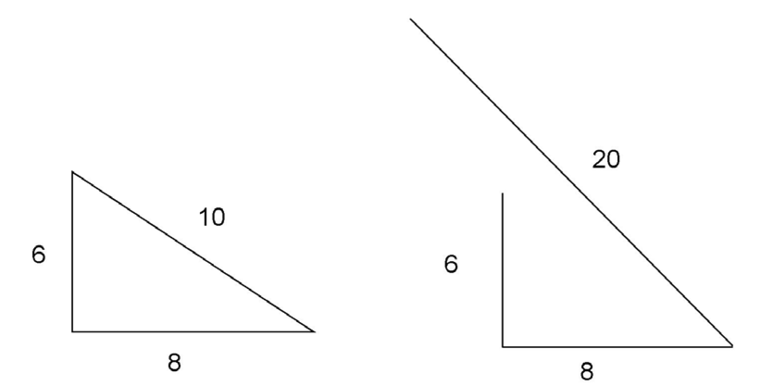
Practice Questions

1. A triangle has two sides that measure 4 centimeters and 7 centimeters. What is the largest possible whole number length of the third side?

2. A triangle has two sides that measure 3 feet and 6 feet. What is the smallest possible whole number length of the third side?

Solutions

1. The largest possible whole number length of the third side is 10 centimeters.

The lengths of the first two legs of the triangle add up to 11 centimeters. The third leg must be smaller than 11 centimeters, so it can measure 10 centimeters at most.

2. The smallest possible whole number length of the third side is 4 feet.

The lengths of any two sides of a triangle must always add up to more than the remaining side. The third side could not measure 3 feet, because 3 + 3 is not more than 6 feet. The third side would have to measure at least 4 feet.

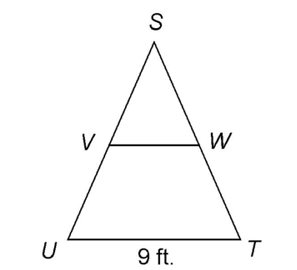
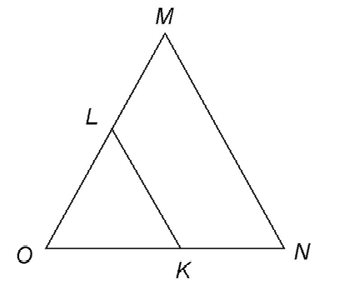
Triangle midsegments

If you draw a line between the midpoints of any two sides of a triangle, you create what is known as a triangle midsegment. In this triangle, is a midsegment:

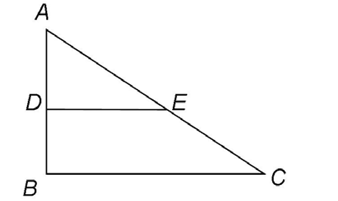
The midsegment of a triangle is always parallel to the third side and half its length.

Example

In ABC, midsegment DE is parallel to side 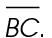Since BC = 10, we know that DE = 5.

Practice Questions

1. In STU, 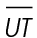measures 9 feet. What is the length of midsegment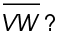

2. Midsegment 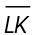is parallel to side 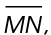as shown in the figure. If 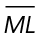measures 8 inches, what is the length of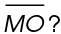

Solutions

1. The length of 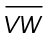is 4.5 feet.

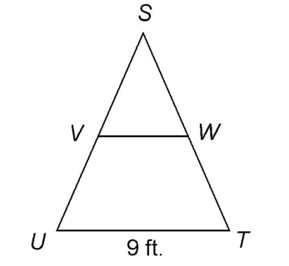
Since 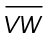is a midsegment of the triangle, it is parallel to 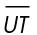and equal to half its length. So, 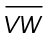measures half of 9, or 4.5 feet.

2. The length of 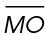is 16 inches.

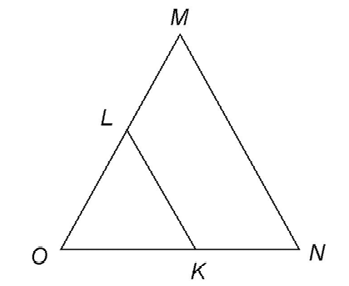
Midsegments connect the midpoints of two sides of a triangle. Thus, we know that L is a midpoint of If ML = 8 inches, then MO = 16 inches.

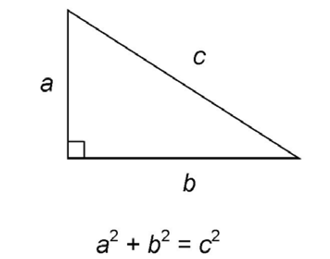
The Pythagorean theorem

Before we leave this chapter on Triangles, there is one concept left to cover. This might be the most important concept you learn in geometry.

This concept is the Pythagorean theorem. It is named after the ancient Greek scholar Pythagoras, who developed it many years ago.

The Pythagorean theorem appears on geometry tests often. To do well on these tests, you must understand it. We’ll cover the basics here.

Formula

Pythagoras was a brilliant scholar. He created a formula that changed math forever.

One day, Pythagoras was contemplating right triangles. He noticed an interesting relationship between the sides. He labeled the sides like this:

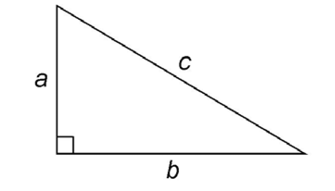
In his labeling, side c was always across from the right angle. The other two sides were sides a and b.

Pythagoras realized that if you knew the lengths of two sides of a right triangle, you could always find the length of the third side. This is how.

First, you multiply the length of side a by itself:

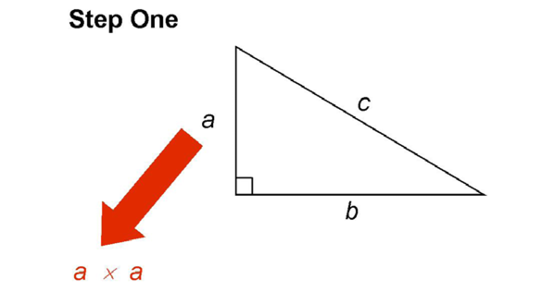
This produces a × a, or a2.

Next, you multiply the length of side b by itself:

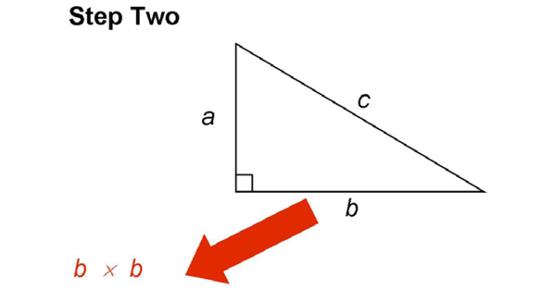
This produces b x b, or b2.

Third, you multiply the length of side c by itself:

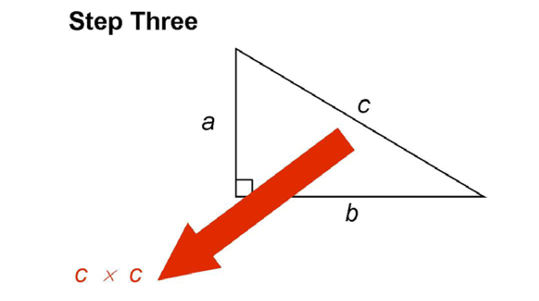
This gives you c2.

Once you have these three values, a2, b2, and c2, create an equation: a2 + b2 = c2.

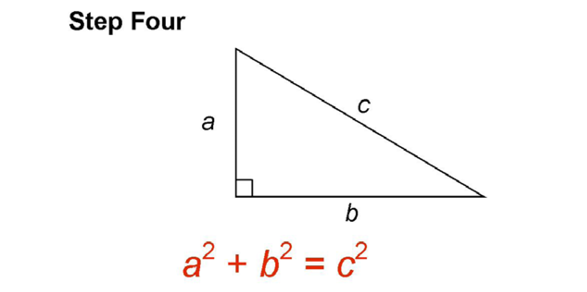
This is Pythagoras’ famous formula. It became widely used in all of geometry.

To be honest, the “story” of how the formula was developed is . . . well, it’s made up. But the theorem itself is completely true.

Example

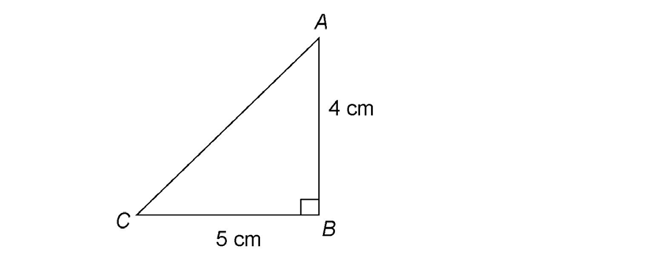
Here is an example of how the Pythagorean theorem works. Say you want to find the length of side c in the right triangle:

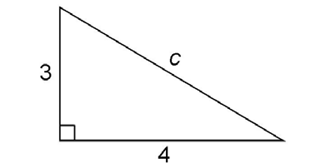
Side c is the longest side, or hypotenuse.

We know from the figure that a equals 3 and b equals 4. Plug these into the formula:

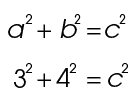
To find the length of c, solve the equation:

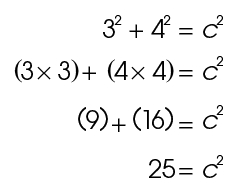
Now we know that 25 equals c × c. What number multiplied by itself equals 25?

5 × 5 = 25

The length of c is 5.

Practice Questions

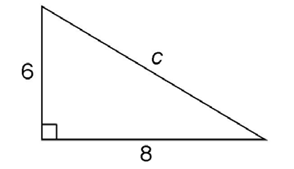
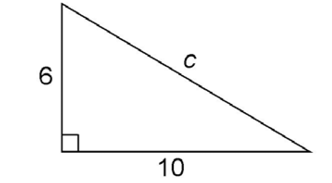
1. Using the Pythagorean theorem, find the length of c in the right triangle shown.

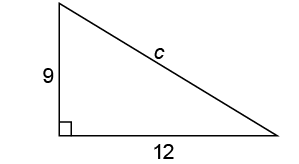
2. Using the Pythagorean theorem, find the length of c in the right triangle shown.

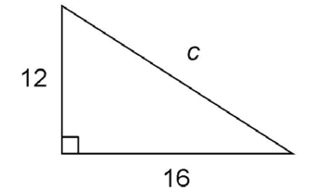
3. Using the Pythagorean theorem, find the length of c in the right triangle shown.

4. What is the length of the hypotenuse of the triangle shown?

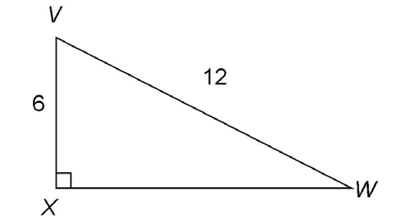
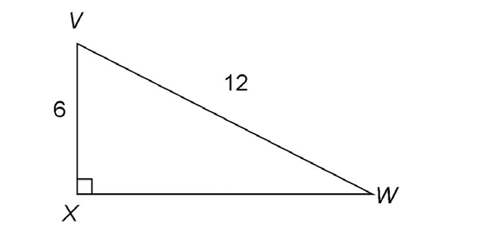
5. If VX = 6 and VW = 12, what is the length of side XW?

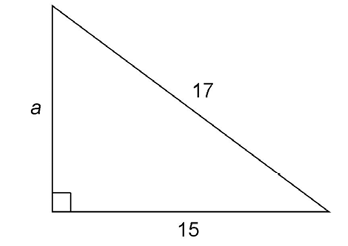
6. What is the value of a in the figure shown?

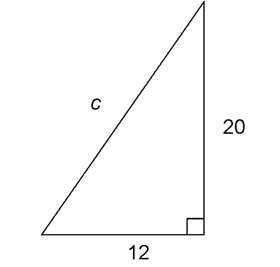
7. The triangle shown has legs measuring 20 inches and 12 inches. What is the length of the hypotenuse, c?

8. What is the length of ?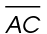

Solutions

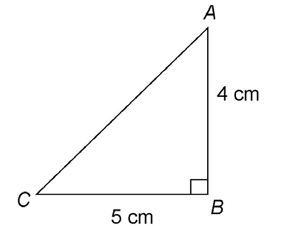
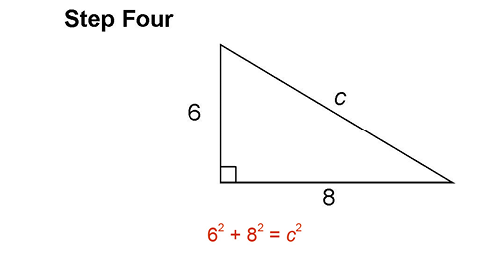
1. First, multiply the length of one side by itself. Let’s start with the shorter side, 6.

This produces 6 × 6, which can be written as 62.

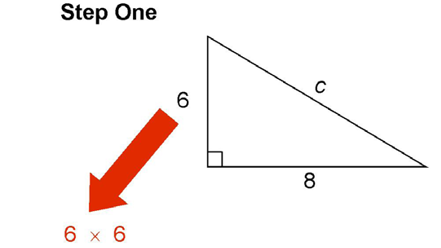
Next, multiply the length of the other side by itself:

This gives us 82.

Third, multiply the length of side c by itself:

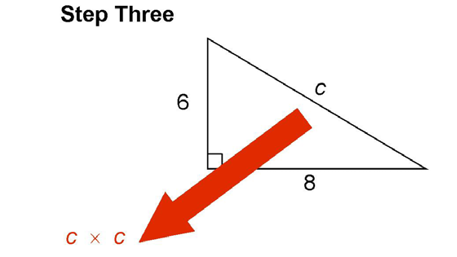
This gives us c2.

Now, add together 62 + 82. These are equal to c2.

Then solve the equation to find the length of c.

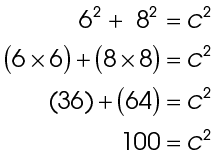
What number multiplied by itself equals 100?

10 × 10 = 100

The length of c is 10.

2. We know from the figure that one side equals 9 and another side equals 12. Which side is a and which is b? Let’s call the smaller side a. Plug these into the formula:

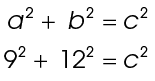
To find the length of c, solve the equation:

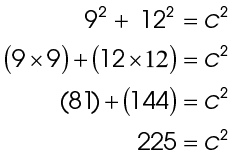
This tells us that c × c equals 225. What number multiplied by itself equals 225?

15 × 15 = 225

The length of c is 15.

3. Using the Pythagorean formula, set up an equation:

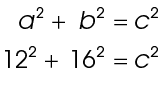
Now, solve the equation to find the length of c.

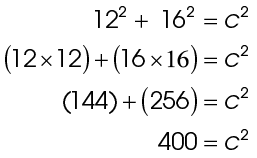
What number multiplied by itself equals 400?

20 × 20 = 400

The length of c is 20.

4. The length of the hypotenuse is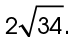

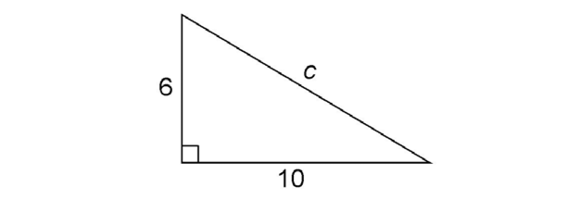
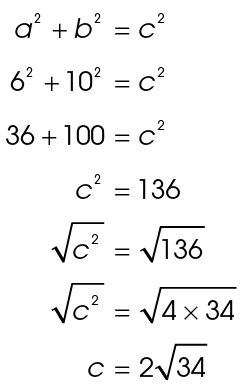
5. Side XW measures 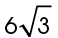units.

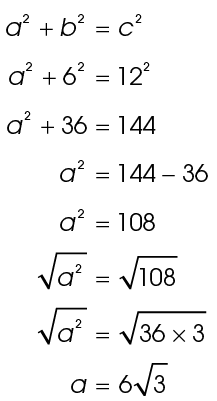
6. The value of a is 8.

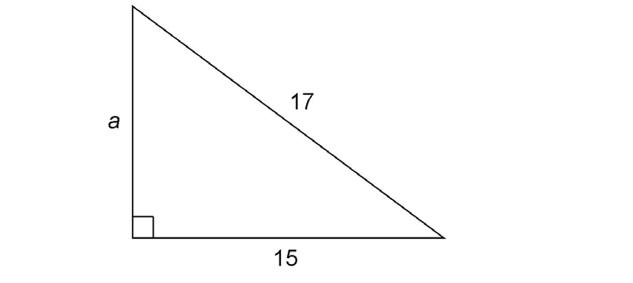
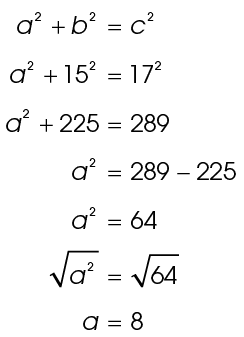
7. The hypotenuse measures 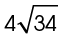inches.

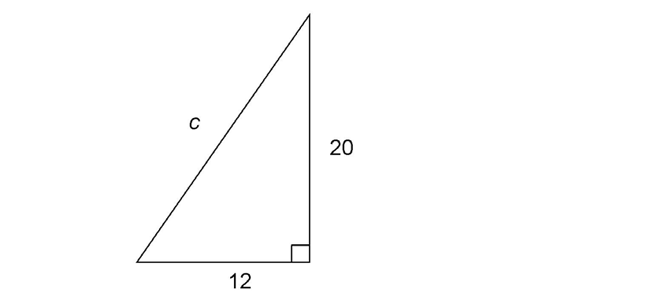
8. The length of 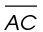is 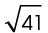centimeters.

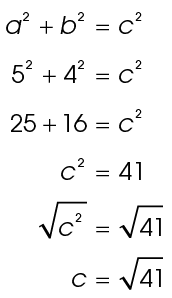
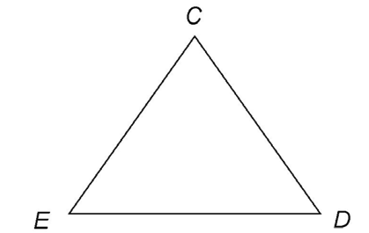
Chapter Review

1. Triangle CDE is equilateral. What is the measure of D?

2. What is the measure of 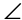T?

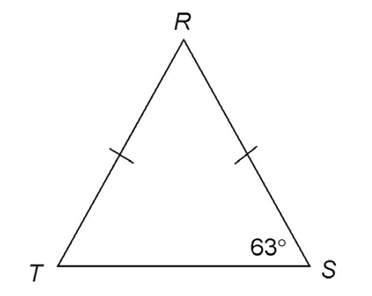
3. What is the perimeter of the triangle below?

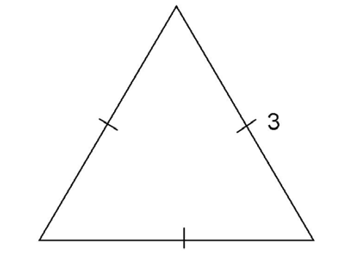
4. What is the area of the triangle shown?

5. What is the formula for the Pythagorean theorem?

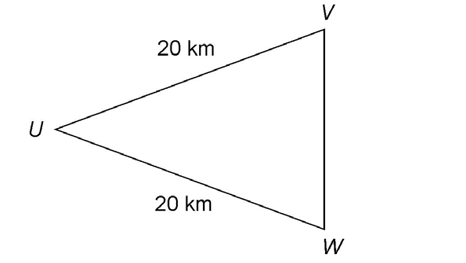
6. Three points are located in a triangular pattern, as shown in the figure. If the perimeter of the triangle is 64 kilometers, what is the distance from point V to point W?

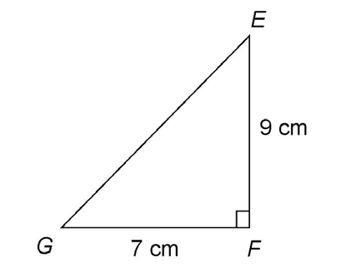
7. Right triangle EFG has legs measuring 9 centimeters and 7 centimeters, as shown. What is the area of the triangle?

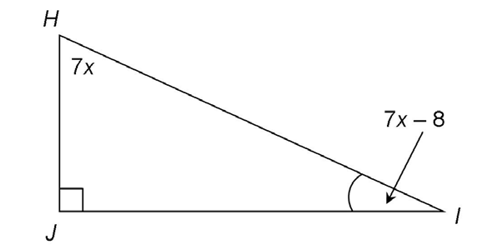
8. If H measures 7x and I measures 7x – 8, what is the value of x in the figure shown?

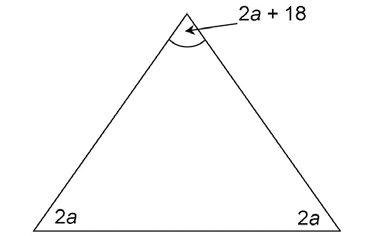
9. The triangle shown has three angles measuring 2a, 2a, and 2a + 18, as shown. What are the measures, in degrees, of the three angles?

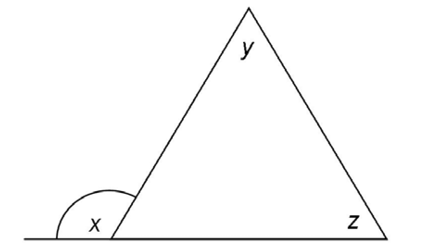
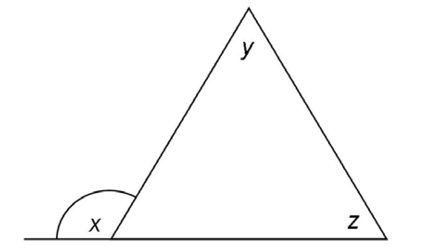
10. In the triangle shown, if y measures 62° and z measures 58°, what is the measure of exterior angle x?

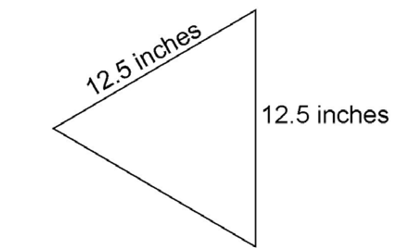
11. Allejandra cuts a wooden shelf in the shape of a triangle, as shown. The perimeter of the shelf is 37.5 inches. What are the measures, in degrees, of each of the shelf’s three angles?

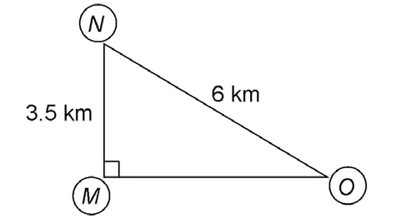
12. In the city of East Harbor, three buildings are located in a triangular arrangement, as shown. If Building N is 6 kilometers northwest of Building O and 3.5 kilometers north of Building M, Building M is approximately how many kilometers west of Building O?

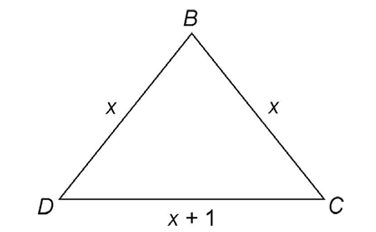
13. Victor creates a triangle by placing three metal rods in the pattern shown. The perimeter of the triangle is 16 feet. What is the length of each metal rod Victor uses?

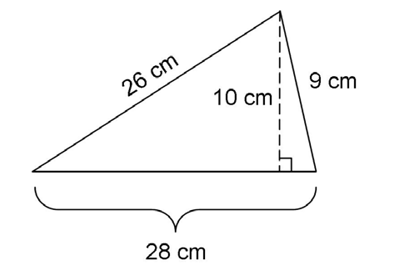
14. Jennifer cuts a piece of fabric in the shape of a triangle. The measurements are shown in the figure. What is the area of the triangle she cuts?

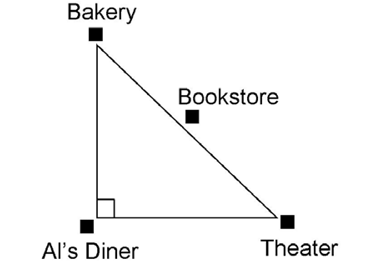
15. On the city map shown, the bookstore lies exactly halfway between the bakery and the theater. If Al’s Diner is located 2 miles from both the bakery and the theater, how far is the bookstore from the bakery?

Solutions

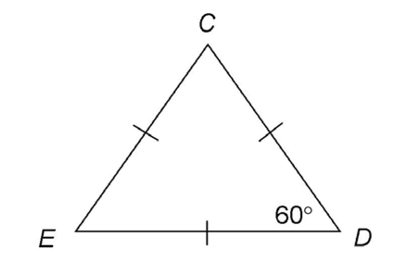
1. Triangle CDE is an equilateral triangle. All of its angles measure 60.°

2. This is an isosceles triangle, with two equal sides and two equal angles. Side TR equals side SR, so T equals S. The measure of T is 63°.

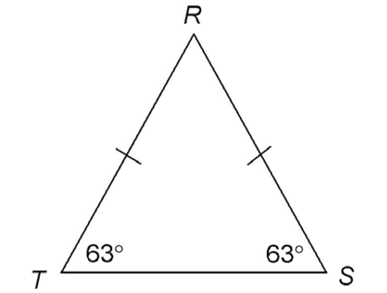
3. This triangle has three equal sides. That means all sides measure 3. The perimeter is 3 + 3 + 3, or 9.

4. To find the area, use the area formula: 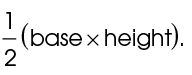The area is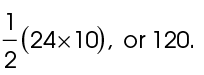

5.

6. The distance from point V to point W is 24 kilometers.

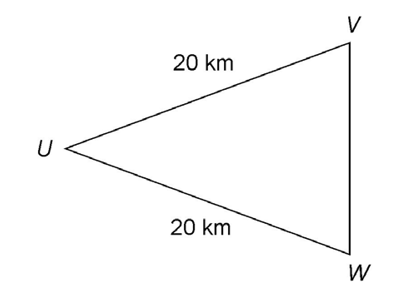
We are given the perimeter, 64 kilometers, and the lengths of two sides. Subtract the lengths of the two given sides to determine the distance from V to W: 64 kilometers – 20 kilometers – 20 kilometers = 24 kilometers.

7. The area of the triangle is 31.5 square centimeters.

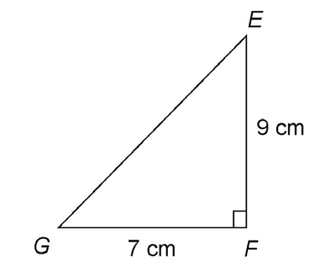
Use the area formula, 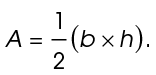Substitute 7 for the base and 9 for the height of the triangle:

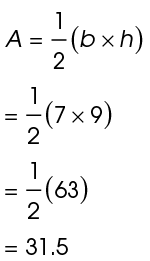
8. The value of x is 7°.

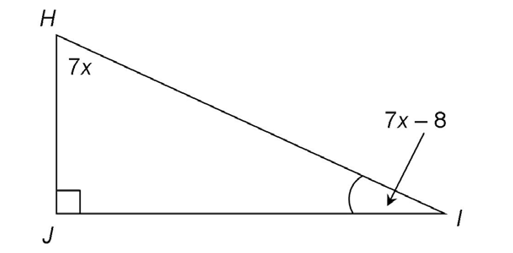
Angles H and I are complementary, so their measures add up to 90°. The remaining angle of the triangle is a right angle, and all three angles of the triangle add up to 180°, so mH plus mI must equal 90°:

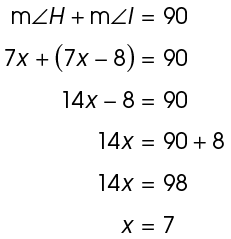
9. The three angles measure 54°, 54°, and 72°.

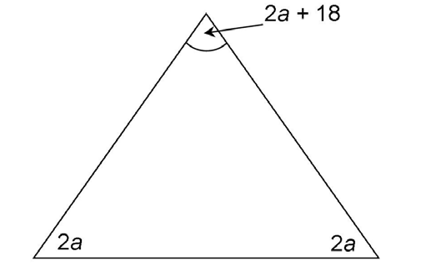
First, find the value of a. The measures of the interior angles of a triangle add up to 180°. Use this information to set up an equation and solve for a:

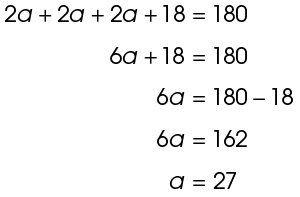
Now that we know the value of a, we can plug this into the expressions shown. The two smaller angles measure 2 times 27, or 54°. The larger angle, at the top of the triangle, measures 2(27) + 18, or 72°.

10. The measure of exterior angle x is 120°.

Angle x is an exterior angle, so its measure equals the sum of the two non-adjacent interior angles. Set up an equation to solve for x:

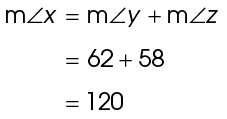
11. The shelf’s angles each measure 60°.

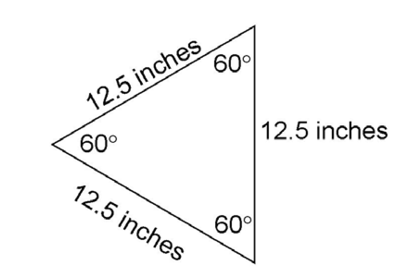
The perimeter of the shelf is 37.5 inches. Subtract the lengths of the given sides from the perimeter: 37.5 – 12.5 – 12.5 = 12.5. The remaining side of the shelf also measures 12.5 inches.

Since all three side lengths are equal, this shelf forms an equilateral triangle. The measures of its three angles are equal. Each angle therefore measures 60°.

12. Building M is approximately 4.873 kilometers west of Building O.

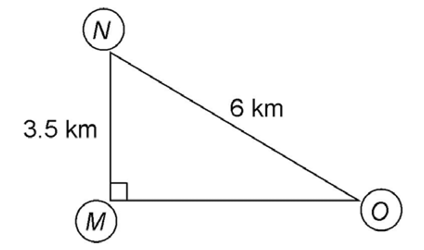
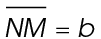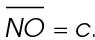Use the Pythagorean theorem to solve this problem. Let and Solve for the measure of 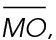which is represented by a in the equation:

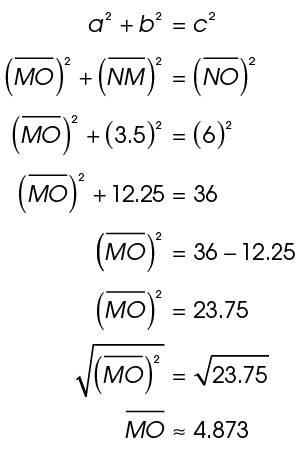
13. The lengths of the metal rods are 5 feet, 5 feet, and 6 feet.

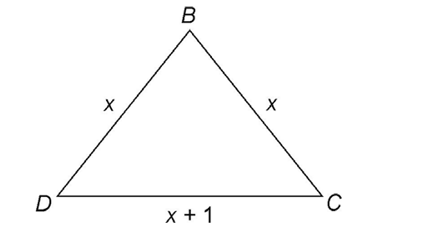
Using the formula for the perimeter of a triangle, set up an equation:

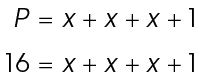
Solve for x:

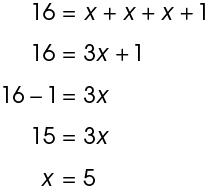
The value of x is 5, so sides each measure 5 feet. Side measures 5 + 1, or 6 feet.

14. The area of the fabric is 140 square centimeters.

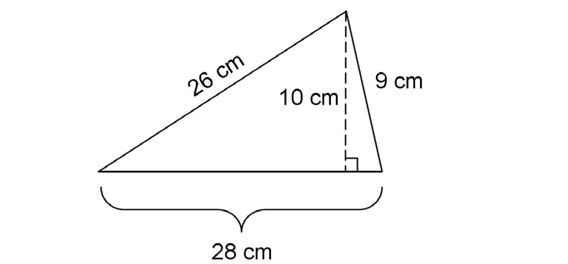
Use the length of the perpendicular line, 10 centimeters, for the height of the triangle. Use 28 centimeters as the length of the base.

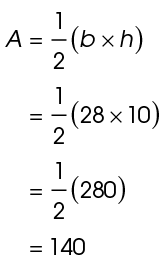
15. The bookstore is 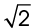miles from the bakery, or approximately 1.414 miles.

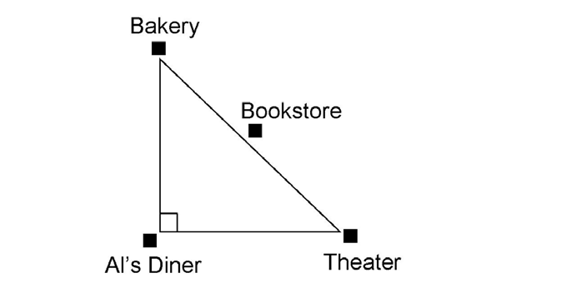
Use the information you are given to find the distance from the bakery to the theater. This is the length of the hypotenuse of the triangle. Plug 2 in for a and b in the Pythagorean theorem:

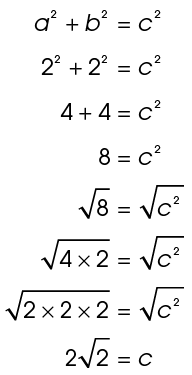
The distance from the bakery to the theater is 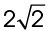miles. Half of this distance would be 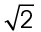miles.