Chapter 6

Special Right Triangles

Hi! I’m egghead. I will teach the following concepts in this chapter:

What is a special right triangle?

Certain types of right triangles appear often in geometry. They are called special right triangles. We will look at three main types.

Three main types of special right triangles

One type of special right triangle is called the 45-45-90° triangle. This is a right triangle with interior angles of 45, 45, and 90 degrees.

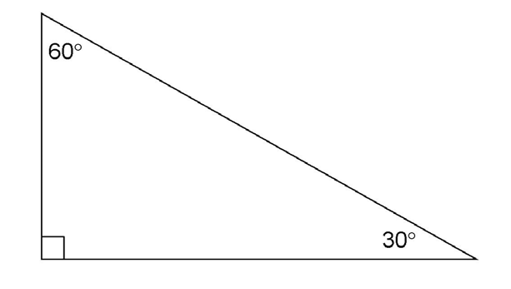
A second type of special right triangle is called the 30-60-90° triangle. These triangles have interior angles of 30, 60, and 90 degrees.

A third type of special right triangle is called the Pythagorean triple.

These triangles have three sides with certain lengths, based on the Pythagorean theorem. There are four common Pythagorean triples:

Now let’s take a look at the properties of each special right triangle.

Common square roots

Before we start, there are two common square roots that you should know. These are the values for 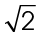and .

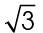On some questions, you can leave the square root sign right in the answer. On other questions, you have to give an approximate number.

The value for 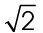is approximately 1.414. It’s actually a decimal number that goes on forever, but 1.414 is all you need to remember.

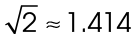
The value for 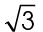is approximately 1.732. This value is also an infinite decimal number, so 1.732 is close enough.

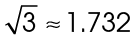
These two square roots come up often when dealing with special right triangles, so it's helpful to memorize their values.

45-45-90 triangles

The 45-45-90 triangle has two equal angles. It is an isosceles right triangle.

The sides across from the 45° angles are also equal. The sides of a 45-45-90 triangle always have the same ratio: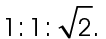

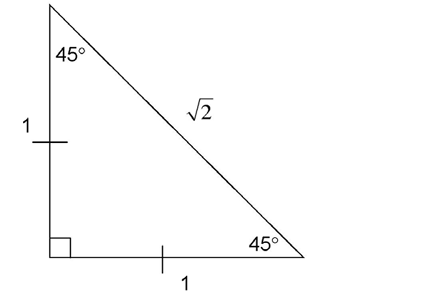
This does not mean that the sides of a 45-45-90 triangle will always measure 1, 1, and 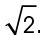It means that the sides will always be in a ratio of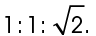

Here are some examples to show you how this works.

Examples

If one leg of a 45-45-90 triangle measures 1 inch, the other leg will measure 1 inch.

The hypotenuse will measure 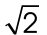inches.

If one leg of a 45-45-90 triangle measures 2 feet, the other leg will measure 2 feet.

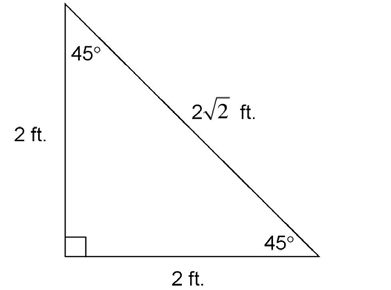
The hypotenuse will measure 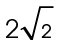feet.

The sides across from the 45° angles always measure the same length as each other. The hypotenuse always measures the same length as one leg × .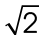

30-60-90 triangles

Unlike 45-45-90 triangles, the 30-60-90 triangle has no equal angles, and it’s not isosceles. However, it does have some important properties to know about.

The sides of a 30-60-90 triangle are always in the ratio of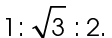

The side across from the 30° angle always has the smallest measure. The side across from the 90° angle always has the largest measure. The side across from the 60° angle has the measure in between.

This is easier to remember if we use estimation. The value for 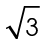is approximately 1.732, which is greater than 1 but less than 2.

Examples

If the shortest leg of a 30-60-90 triangle measures 1 foot, the other leg will measure 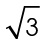feet.

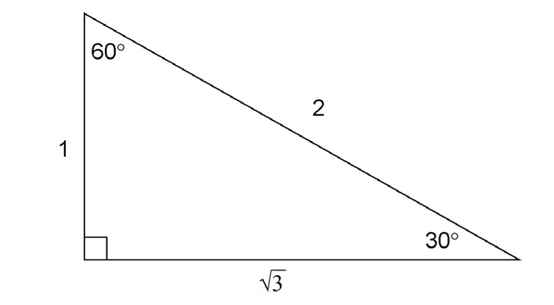
The hypotenuse will measure 2 feet.

If the shortest leg of a 30-60-90 triangle measures 4 inches, the other leg will measure 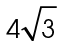inches.

The hypotenuse will measure 8 inches.

If the shortest leg of a 30-60-90 triangle measures 7 meters, the other leg will measure meters.

The hypotenuse will measure 14 meters.

The side across from the 60° angle always measures 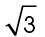times the length of the shortest leg. The hypotenuse always measures 2 times the shortest leg.

Finding angles

We can use the properties of 45-45-90 and 30-60-90 triangles to find the measure of angles and lengths. What is the measure of y in the figure shown?

This is a 45-45-90 triangle. We know this because it has two equal sides. The two sides lie opposite the equal angles, so y must measure 45°.

What is the measure of z in the figure shown?

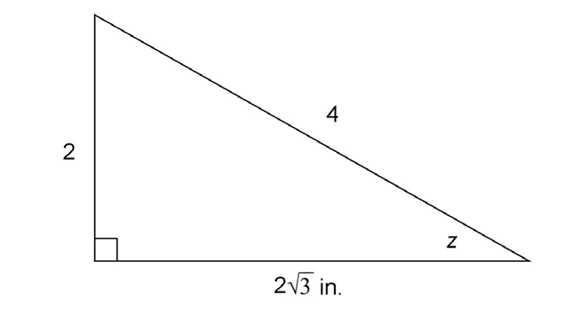
This is a 30-60-90 triangle. We know this because the sides are in a ratio of 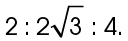If we divide each of the side lengths by 2, this gives us the ratio of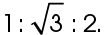

The side marked 2 is the shortest side of the triangle, and z lies opposite the shortest side. So, z must measure 30°.

What is the measure of s in the figure shown?

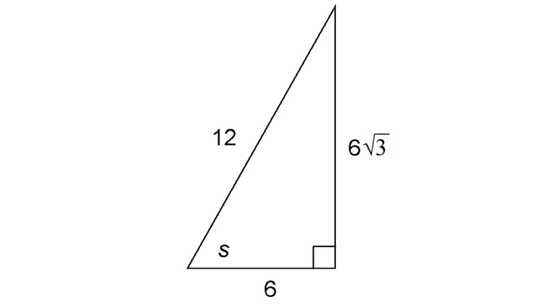
This is a 30-60-90 triangle, with sides in a ratio of 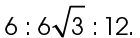If we divide each of the side lengths by 6, this reduces to a ratio of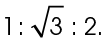

The side marked 6 is the shortest side of the triangle, and the side marked 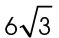is the next largest side. Angle s lies opposite of the side marked 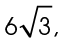so s must measure 60°.

Finding lengths

Triangle properties can help us find side lengths also. What is the length of the other leg in the figure shown?

This is a 45-45-90 triangle, so both legs have the same measurement. The missing leg also measures 4.

The length of the hypotenuse can be determined as well. Its measure is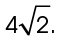

What are the measures of j and k in the figure shown?

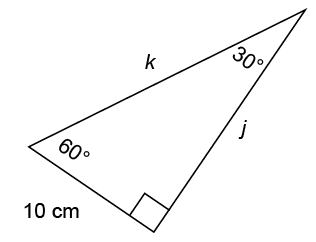
This is a 30-60-90 triangle, so the sides are in the ratio of 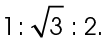We are told that the shortest leg measures 10 centimeters. So, side j must measure 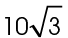centimeters, and k must measure 20 centimeters.

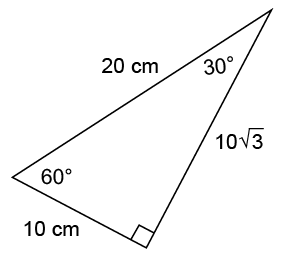
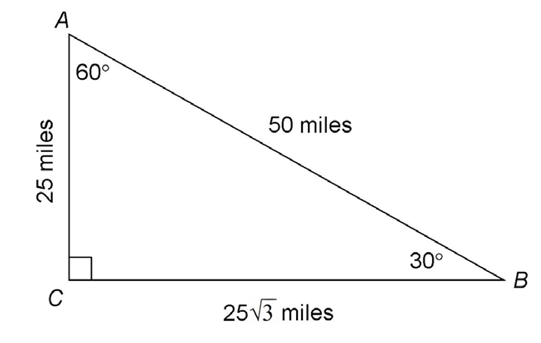
What are the lengths of in the figure shown?

We are told that 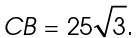This is the side across from the 60° angle. Side 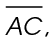across from the 30° angle, must measure 25.

The length of the hypotenuse can be determined as well. Its measure is 2 times the shortest side, or 50.

Practice Questions

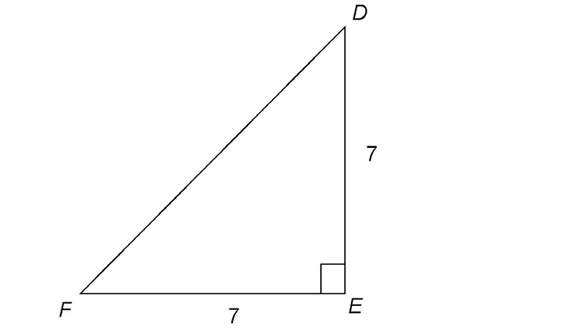
1. What is the measure of DFE in the figure shown?

2. In the figure shown, what is the measure of

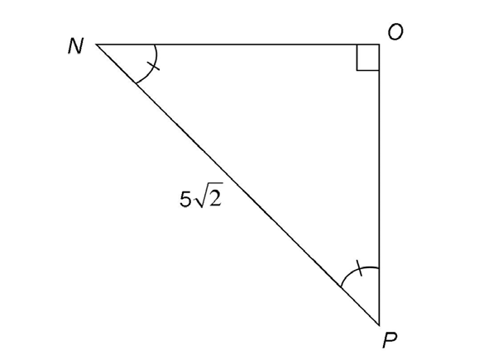
3. In the figure shown, centimeters. What is the length, in centimeters, of

4. What is the measure of QRS in the figure shown?

5. In the figure shown, what is the measure of

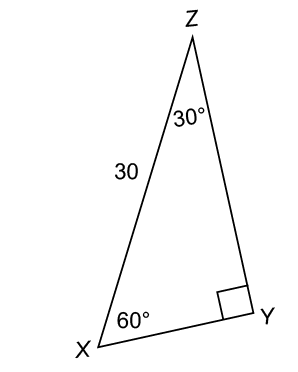
6. In the figure shown, what is the measure of s?

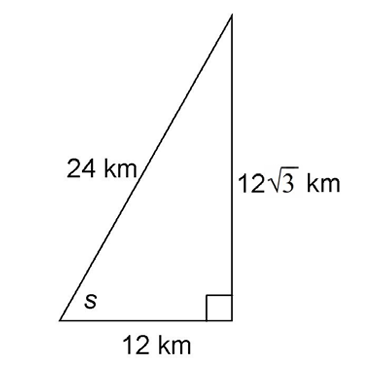
Solutions

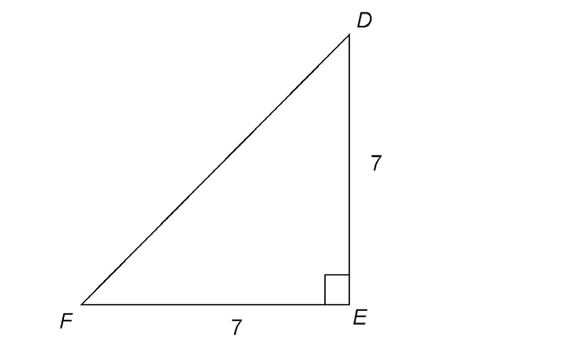
1. The triangle has two equal sides and one right angle, so it is a 45-45-90 triangle. The two smaller angles are equal. Therefore, the measure of DFE is 45°.

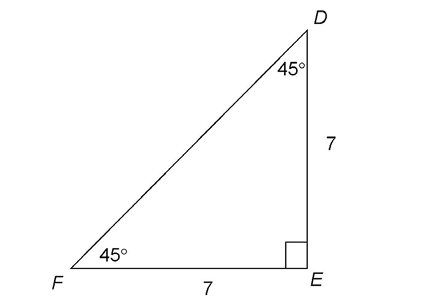
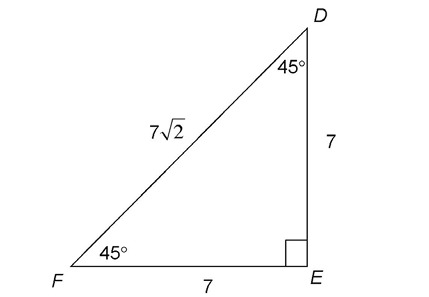
2. Triangle DEF is a 45-45-90 triangle, and both legs measure 7. The hypotenuse is equal to leg × 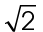. Therefore, the measure of is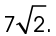

3. This right triangle has two equal angles, so it is a 45-45-90 triangle. The hypotenuse is equal to We are told that centimeters, so both legs measure 5 centimeters.

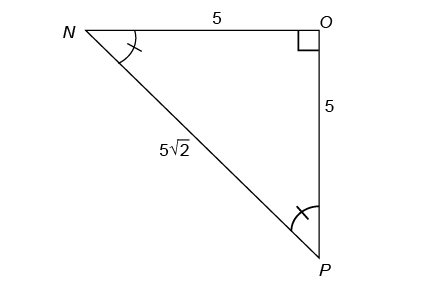
4. The measure of 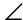QRS is 30°.

The sides of this triangle are in a ratio of 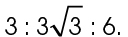If we divide each of the side lengths by 3, this reduces to a ratio of 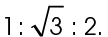So, we have a 30-60-90 triangle.

The side marked 3 is the shortest side of the triangle, and QRS lies opposite this shortest side. That tells us that m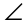QRS = 30.

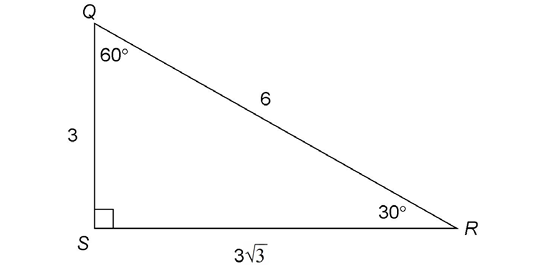
5. The length of 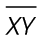is 15.

This is a 30-60-90 triangle, so the sides are in the ratio of 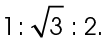The hypotenuse measures 30, and the shortest side measures half of that. Therefore, 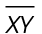measures 15.

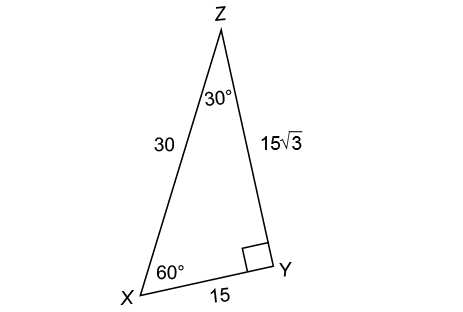
6. The measure of s is 60°.

The sides of this triangle are in a ratio of 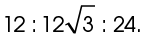We can reduce this to 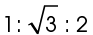if we divide each side by 12. So, this is a 30-60-90 triangle, with 12 kilometers as the shortest side.

The angle marked s is across from the second shortest side, so it must measure 60°.

Pythagorean triples

The third type of special right triangle that we'll review is called the Pythagorean triple. Pythagorean triples are right triangles with side lengths that are positive integers.

Examples

There are an infinite number of Pythagorean triples. In this chapter, we’ll look at four of the most common.

3-4-5 triangles

The smallest Pythagorean triple is the 3-4-5 triangle. This is a right triangle whose side lengths measure 3, 4, and 5:

If you use the Pythagorean theorem to check these side lengths, you’ll see they fit perfectly:

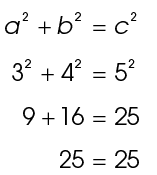
6-8-10 triangles

Another Pythagorean triple is the 6-8-10 triangle. The legs of this triple are multiples of the 3-4-5 triangle. Take each side of the 3-4-5 triangle and multiply it by 2. This gives you a triangle with side lengths 6, 8, and 10.

Other triplets in this series include 9-12-15 and 12-16-20.

5-12-13 triangles

A third common Pythagorean triple is the 5-12-13 triangle. This triangle has legs of length 5, 12, and 13. Other multiples are 10-24-26 and 15-36-39.

8-15-17 triangles

The fourth common Pythagorean triple is the 8-15-17 triangle. Again, there are many multiples of this, but 8-15-17 is most important to remember.

Finding lengths

Knowing some Pythagorean triples gives you a shortcut to finding the lengths of the sides of certain right triangles. When you recognize a triple, you don’t have to use the Pythagorean theorem to find the length of a missing side.

For example, in the figure below, we don’t have to calculate to find the value of c. This is a right triangle with legs of length 3 and 4. It is a 3-4-5 Pythagorean triple, so c must measure 5.

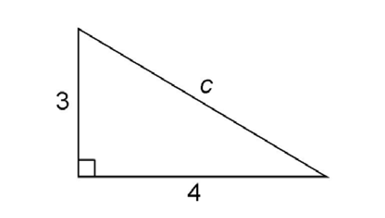
Similarly, in the figure below, we can find the length of a just by recognizing the Pythagorean triple. This is a 6-8-10 Pythagorean triple. So, the length of a is 6.

Practice Questions

1. What is the length of b in the figure shown?

2. What is the length of 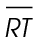in the figure shown?

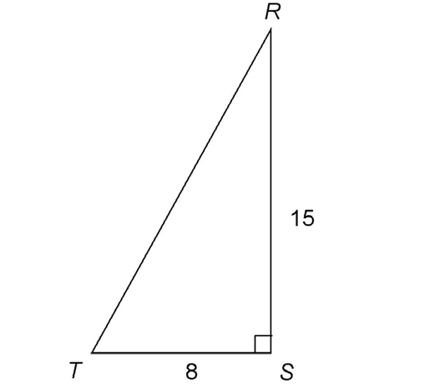
3. Find the value of x in the figure shown.

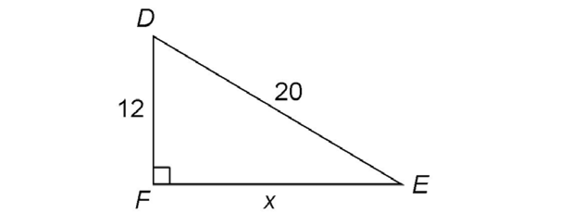
4. Find the length of the missing side in the figure shown.

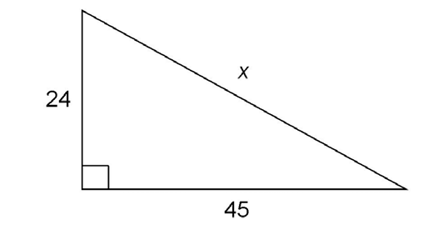
5. Find the length of the missing side.

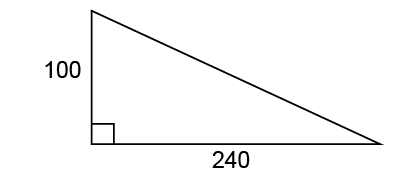
6. Find the length of the missing side.

Solutions

1. The length of b is 12. This Pythagorean triple has sides of length 5, 12, and 13. So, the missing side (side b) must measure 12.

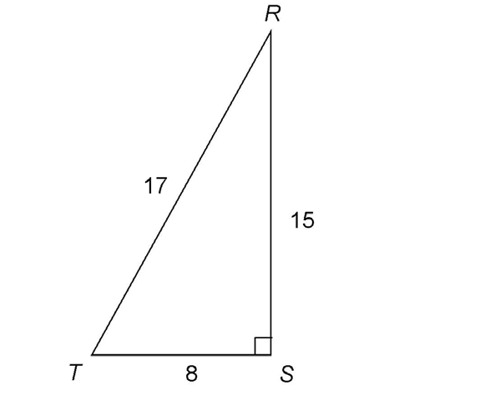
2. The length of is 17. This is an 8-15-17 Pythagorean triple. The hypotenuse measures 17.

3. The value of x is 16. You are given the lengths of two sides, 12 and 20. Both of these sides are multiples of a 3-4-5- triangle. The lengths are 4 times as long as the 3-4-5 lengths. For leg 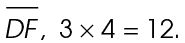For hypotenus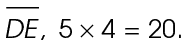e Side 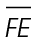must also be a multiple: 4 × 4 = 16.

4. This is a multiple of an 8-15-17 triangle. The lengths of the sides are three times as long as the sides of an 8-15-17 triangle. If we multiply 8 by 3, we get 24. If we multiply 15 by 3, we get 45. The missing length is therefore 3 × 17, or 51.

5. This is a multiple of a 5-12-13 triangle. The lengths 100 and 240 are 20 times the lengths of the corresponding sides of a 5-12-13 triangle. So the missing length is 20 × 13, or 260.

6. This triangle is a multiple of a 6-8-10 Pythagorean triple. The sides marked 60 and 100 are 10 times the lengths of the corresponding sides of a 6-8-10 triangle. The missing length is therefore 8 × 10, or 80.

Chapter Review

1. What is the measure of LMN in the figure shown?

2. What is the measure of hypotenuse 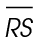in the figure shown?

3. What is the length of 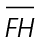in the figure shown?

4. Jordan’s house is the same distance from the gym as it is from his school. He lives 3 miles from both the gym and school, as shown. What is the distance, in miles, from the gym to the school?

5. Aimee folds a napkin in the dimensions shown. The top corner of the napkin forms a right triangle. What is the length, in inches, of n?

6. What is the measure of KLM in the figure shown?

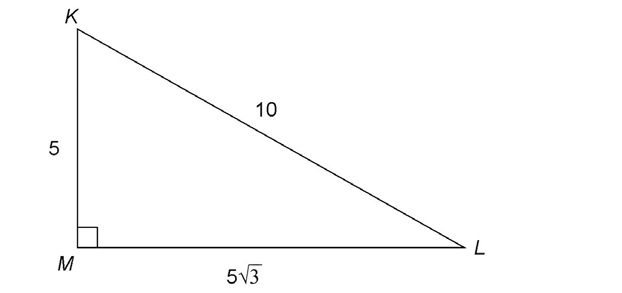
7. In the figure shown, what is the measure of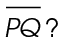

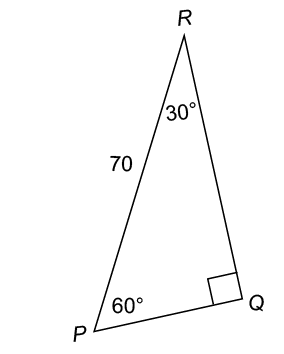
8. What is the measure of w in the figure shown?

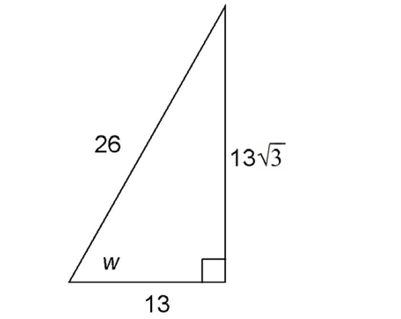
9. Allen delivers packages to delivery stops B, C, and D, shown in the figure below. He starts at stop C and drives 19 miles north to stop D. He then drives 38 miles southeast to stop B. He realizes he forgot to get a delivery signature at stop C, so he drives back to stop C from stop B. How many miles must he travel due west to return to stop C?

10. In the figure shown, what is the measure of ?

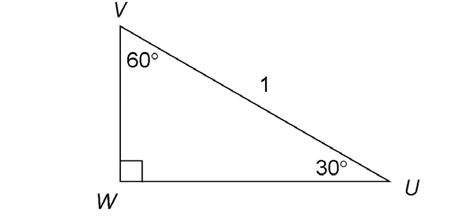
11. What is the measure of 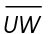in the figure shown?

12. What is the length of m in the figure shown?

13. What is the length of 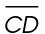in the figure shown?

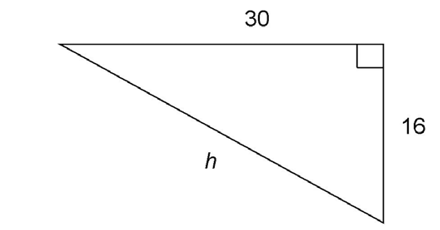
14. Find the value of h in the figure shown.

15. Brandy cuts two pieces of construction paper for a collage. The pieces of paper are shaped like triangles, as shown. What are the lengths of x and y?

Solutions

1. Triangle LMN has two equal sides and one right angle, so it is a 45-45-90 triangle. The two smaller angles are equal. Therefore, the measure of 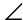LMN is 45°.

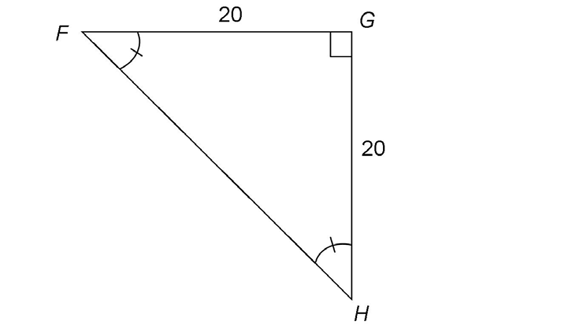
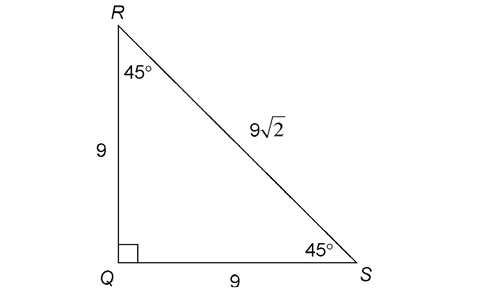
2. Triangle QRS is a 45-45-90 triangle, with two legs of length 9. The hypotenuse 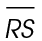is equal to leg × 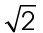. Therefore, 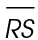measures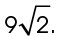

3. Triangle FGH is a 45-45-90 triangle. We know this because it has two equal angles and two equal sides. The sides of a 45-45-90 triangle are always in a ratio of 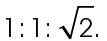Hypotenuse 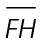is therefore equal to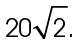

4. The distance from the gym to the school is 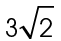miles. The three buildings form an isosceles right triangle, as shown in the figure. The two legs of the triangle measure 3. The smaller angles both measure 45°.

The sides of a 45-45-90 triangle are always in a ratio of 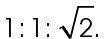That means the hypotenuse equals leg × 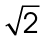. So the distance from the gym to the school, the hypotenuse of the triangle, is

5. The length of n is

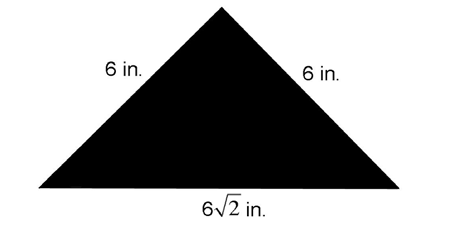
The napkin forms an isosceles right triangle. The side across from the 90° angle, the hypotenuse, is equal to the leg × 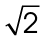. The hypotenuse therefore measures or approximately 8.48 inches.

6. The measure of KLM is 30°.

The sides of this triangle are in a ratio of 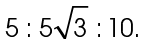If we divide each of the side lengths by 5, this reduces to a ratio of 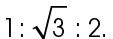This means KLM is a 30-60-90 triangle.

The side marked 5 is the shortest side of the triangle, and KLM lies opposite this shortest side. So, we know that m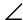KLM = 30.

7. The length of 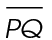is 35.

This is a 30-60-90 triangle with sides in the ratio of The hypotenuse measures 70, and the shortest side measures half of 70. Therefore, 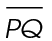measures 35.

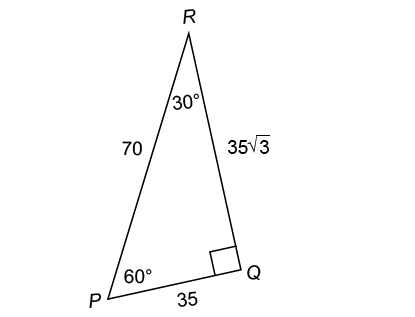
8. The measure of w is 60°.

This triangle has sides in a ratio of 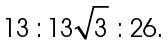We can reduce this to 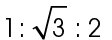if we divide each side by 13. This is therefore a 30-60-90 triangle.

We are asked for the measure of w, which lies across from the second shortest side. The measure of w must be 60°.

9. Allen must travel 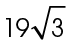miles to return to stop C.

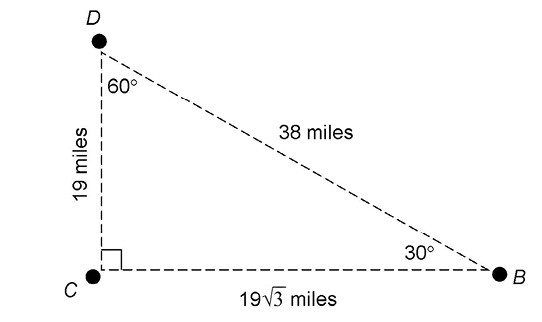
The triangle created by Allen’s path is a 30-60-90 triangle. We are given the lengths of two of the sides: 19 miles (for the shortest leg) and 38 miles (for the hypotenuse). The side across from the 60° angle is equal to the length of the shortest leg × which in this case equals 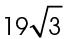miles.

10. The measure of 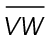is 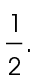It can also be written as a decimal number.

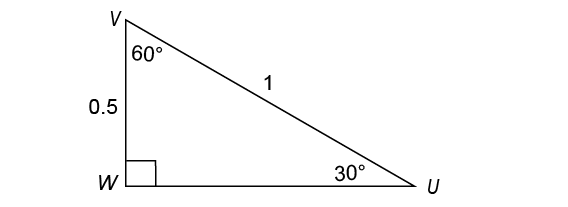
Every 30-60-90 triangle has sides in a ratio of 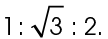Triangle UVW is no exception. In this case, the longest side measures 1. So, the shortest side must measure half of that, or 0.5.

11. The measure of is It can also be written as a decimal number.

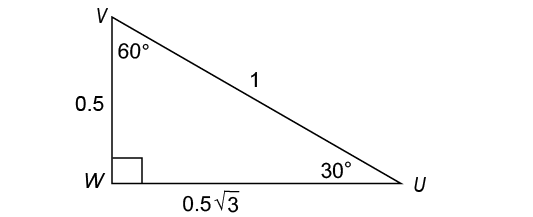
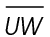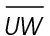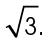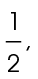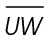In this triangle, side lies opposite the angle measuring 60°. So, the measure of side will equal the length of the shortest leg times The shortest leg measures so measures 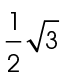in fractional form. In decimal form, this is written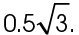

12. The length of m is 24. The triangle is a multiple of the 5-12-13 Pythagorean triple. Each side is twice as long as the side of a 5-12-13 triangle. So, the missing side m measures 2 × 12, or 24.

13. The length of is 25. This triangle is a multiple of the 3-4-5 Pythagorean triple. Each side is 5 times as long as the 3-4-5 triangle sides. Hypotenuse 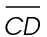therefore measures 5 × 5, or 25.

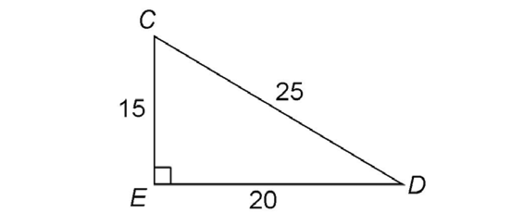
14. The value of h is 34.

This triangle is a multiple of the 8-15-17 Pythagorean triple. Each side is twice as long as the 8-15-17 triangle sides. The length of h, the hypotenuse, is therefore 2 × 17, or 34.

15. The length of x is 8, and the length of y is 12.

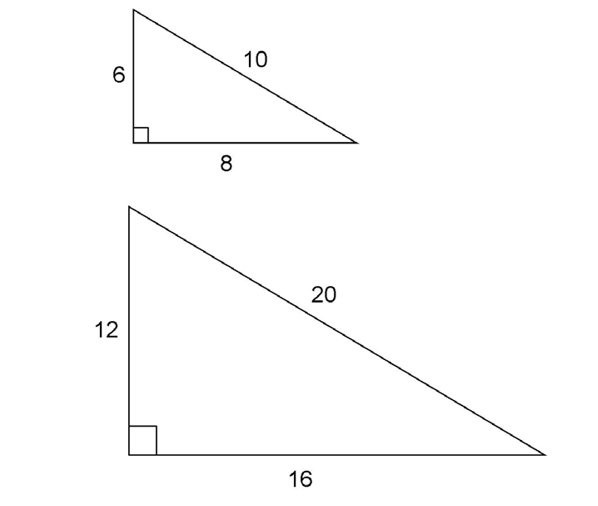
The triangles are both Pythagorean triples. The first is a 6-8-10 triangle, so side x measures 8. The larger triangle has sides exactly twice as long as the sides of the 6-8-10 triangle. Multiply each side of the smaller triangle by 2 to get the side lengths of the larger triangle.

The missing leg, y, measures 2 × 6, or 12.