Chapter 7

Circles

Hi! I’m egghead. I will teach the following concepts in this chapter:

What is a circle?

We all know what a circle looks like. It’s a perfectly round shape that looks like this:

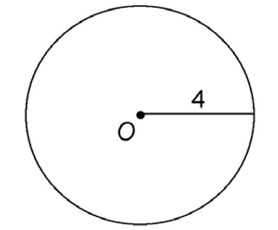
Every circle has a center. Point O lies exactly in the center of the circle shown:

To name a circle, use its center point. The figure above shows circle O.

Every point on the circle is the same distance from the center of the circle:

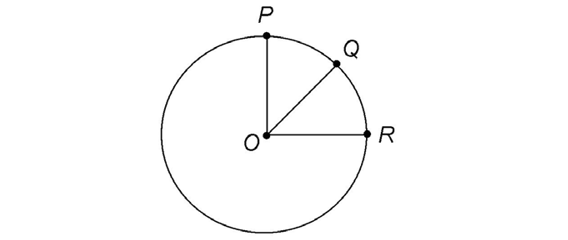
Just like the other shapes we’ve studied, a circle also lies in a two-dimensional plane.

In the diagram below, circle O lies in a plane. Points P, Q, and R lie on the circle.

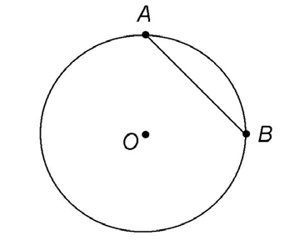
Chord

A chord is a line segment that connects any two points on a circle. In the figure below, you can see chord AB.

Diameter

One important measurement of a circle is a special chord called the diameter. The diameter is the distance from one side of a circle to the other side:

The diameter measures the distance across the circle. It goes through the center of the circle:

You could also draw the diameter across the circle, like this:

It really doesn’t matter where you draw the diameter. It just has to go through the center of the circle.

Examples

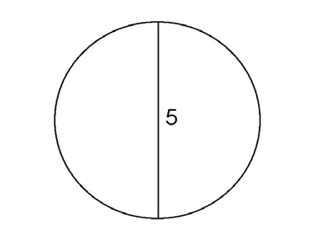
The diameter of this circle measures 9.

This is circle P with diameter AB.

The bigger the circle, the bigger the diameter.

Radius

The radius of a circle is the distance from the center of the circle to its edge:

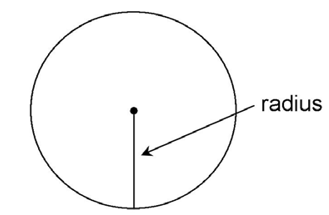
The radius starts at the center of the circle and extends to the outside edge:

This is a radius of circle O.

This is also a radius of circle O.

It doesn’t matter where you draw the radius of a circle. It just has to start at the center of the circle and extend to the outside edge.

Examples

The radius of this circle measures 2:

This is circle P with radius PA and radius PB:

In circle X, radius XY has length 10. Radius XZ has length 10, too.

The radius is exactly 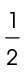the diameter. In circle X, diameter YZ has length 20.

Practice Questions

1. In the space below, draw a circle and label it Q.

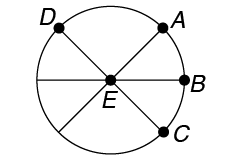
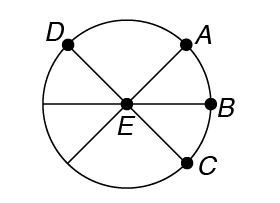
2. What is the name of this circle?

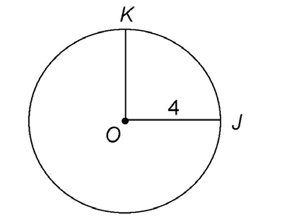
3. In circle O shown, what is the length of radius OK?

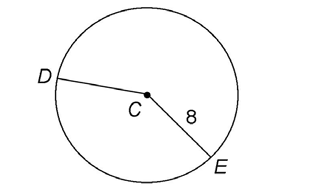
4. In circle C shown, what is the length of radius CD?

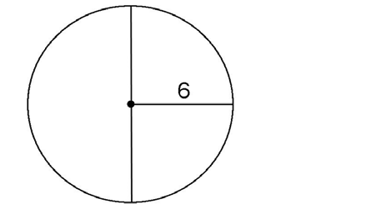
5. In the circle below, what is the length of the diameter?

Solutions

1. The correct answer is shown below.

2. Though there are many chords in this circle, the center point of the circle is E. So the circle is named circle E.

3. In circle O shown, the length of radius OK is also 4. All lines that extend from the center of the circle to its edge have the same measurements.

4. The figure tells us that radius CE measures 8. Every radius on a circle has the same length. So, radius CD must also measure 8.

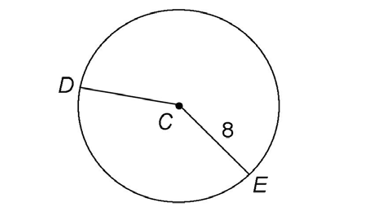
5. In the circle below, we know the radius is 6. The diameter is double the radius, or 12.

Circumference

As we learned in earlier chapters, perimeter is the distance around a shape.

The perimeter of a circle is the distance around its outside edge. This is also called the circumference.

The circumference of this circle is 45:

The circumference of this circle is 22:

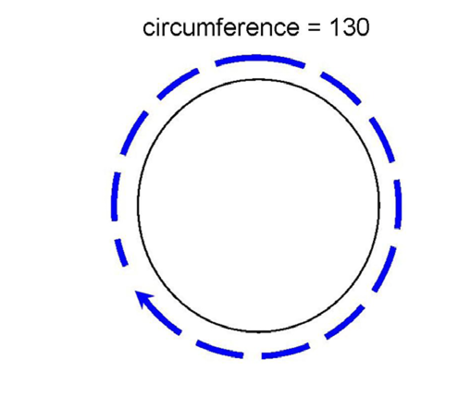
The circumference of this larger circle is 130:

Formula

To find the circumference of a circle, we use this formula:

The Greek letter is a symbol for a certain number. The number is equal to about 3.14. We say “about” because is actually a decimal number that extends into infinity. The long version looks like this:

For short, we say Pi equals approximately 3.14:

The story of how was found is very complex. Many scholars contributed to it. But the Greeks definitely had a lot to do with it, because it ended up with a Greek name!

Some brilliant folks figured out that the circumference of any circle can be found by multiplying by twice the radius.

Yes! Every one!

It turns out that is a magic number in geometry. It helps you find the answers to certain questions. Math is cool like that.

The formula for circumference, again, is:

Here’s the short form:

Examples

Many geometry circle questions ask you to find the circumference.

Here are some examples.

This circle has a radius of length 2:

To find the circumference, multiply 2 × radius × . The radius is 2, so we multiply 2 × 2 × , or 2 × 2. The circumference is 4.

This circle has a radius of length 3:

To find the circumference, multiply 2 × radius × . This time, the radius is 3. So, we multiply 2 × 3 × . The circumference is 6.

Finding radius from circumference

If you know the circumference of a circle, you can also find the radius.

This circle has a circumference of 20

To find the radius, divide the circumference by 2. The circumference is 20, so we divide 20 by 2. The radius is 10.

Here’s another example. This circle has a circumference of 150:

To find the radius, divide the circumference by 2. The circumference is 150, so we divide 150 by 2. The radius is 75.

Practice Questions

1. What is the circumference of circle O?

2. Find the circumference of circle P.

3. Cathy works at the pizza restaurant Little Davey’s. She makes about 15 pizzas an hour in the restaurant's huge wood oven. Each pizza she makes has a radius of 6 inches. What's the total circumference of the 15 pizzas Cathy makes each hour?

4. Johnny and Sally love going to the ice skating rink in the winter. This winter, Sally skated halfway across the circular rink, or 7 feet from the center of the rink to its outside edge. On his first pass, Johnny skated across the entire rink. On his second pass, he skated around the entire rink. How far did Johnny skate on his first two passes combined?

5. In December 1990, a group of folks got together in Norwood, South Africa and constructed the largest pizza ever made up until that time, according to the Guinness Book of World Records. The pizza measured 37.4 meters in diameter. What were its radius and its circumference?

Solutions

1. The circumference is 8.

To find the circumference, multiply 2 × radius × . The radius of circle O is 4. So, we multiply 2 × 4 × :

2 × 4 × = 8

2. To find the circumference, multiply 2 × radius × . The radius of circle P is 6. So, we multiply 2 × 6 × . The circumference is 12.

3. To find the solution, let’s first figure out the circumference of one of Cathy’s pizzas. Each pizza has a radius of 6 inches. To find the circumference of one pizza, we multiply 2 × 6 × = 12. The total circumference of the 15 pizzas must be 180 inches.

4. If Sally skated 7 feet and that measured halfway across the rink, then the rink’s radius is 7 feet. So the circumference is 7 × 2 × = 14. But Johnny also skated twice as far as Sally, so we need to add another 14 feet. Johnny skated a total of 14 + 14 feet.

5. If the diameter of the pizza was 37.4 m, then its radius is that, or 18.7 m. Its circumference is just 37.4 × = 37.4 meters.

Finding area

Along with circumference, the next major topic to know about circles is how to find the area.

The dotted line shows the circumference of the circle. The shaded section shows the area:

The larger the circle, the more space it takes up.

Formula

To find the area of a circle, we use this formula:

Yes—another cool math concept. If you multiply the radius of any circle by itself, and then multiply that by , you get the area.

Here’s the area formula in shorthand:

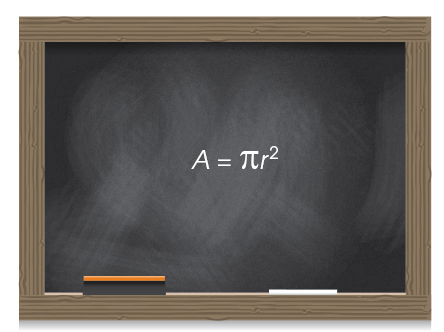
Examples

Let’s look at a couple of examples.

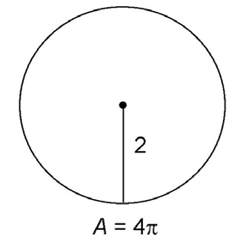
This circle has a radius of length 2 units.

To find the area, multiply × radius × radius. The radius is 2, so we multiply × 2 × 2. The area is 4 square units.

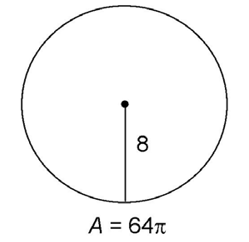
This circle has a radius of length 8 feet.

To find the area, multiply × radius × radius. The radius is 8, so we multiply × 8 × 8. The area is 64 square feet.

Practice Questions

1. What is the area of circle X?

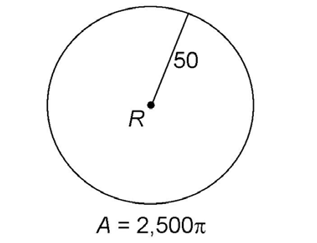
2. Find the area of circle R.

3. Remember the largest pizza ever made in 1990, according to the Guinness Book of World Records? The pizza had a diameter measuring 37.4 meters. What was its area?

4. Find the area of the circle below.

5. Find the area of the circle shown.

Solutions

1. To find the area, multiply × radius × radius. The radius of circle X is 10. So, we multiply × 10 × 10. The area is 100 square units.

2. To find the area, multiply × radius × radius. The radius of circle R is 50. So, we multiply × 50 × 50. The area is 2,500 square units.

3. To find the area, let’s first find the radius. Divide 37.4 by 2 and you get r = 18.7 meters. For the area, multiply × r × r, or 18.7 × 18.7 × = 349.69 square meters.

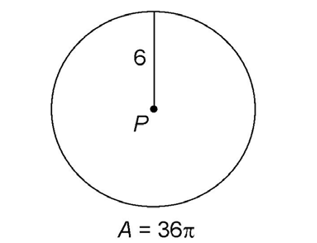
4. The area is 36 square units.

The radius of circle P is 6. So, we multiply × 6 × 6.

5. The circumference is 225 square units.

The radius of circle J is 15. So, we multiply × 15 × 15.

Finding radius from area

When you’re given the area of a circle, you can also find its radius. Just work backward from the information given.

Examples

Circle W shown below has an area of 12. What is the length of its radius?

To answer this question, start with the area formula. Substitute 12 for the value of the area. Then solve for the radius, r.

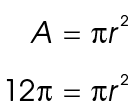
Divide both sides by :

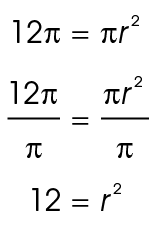
The ’s drop out, and we are left with 12 = r 2. To find r, take the square root of both sides:

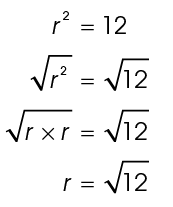
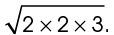The square root of 12 can be broken down even further. The number 12 is the product of 4 times 3. So, This is equal to The square root of 2 times 2 is 2, so take the number 2 out from under the square root sign. The correct answer is

Here’s another example.

Circle E below has an area of 32 square inches. To find the length of its radius, start with the area formula.

We know that the area is 32 square inches. Plug that into the formula:

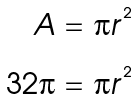
Next, divide both sides by . This leaves 32 = r 2.

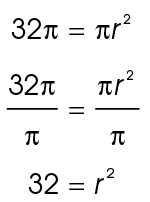
To solve for r, take the square root of both sides:

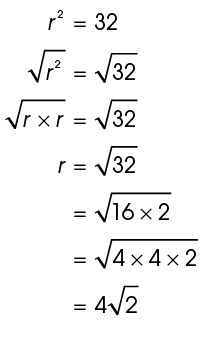
The radius is 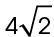inches.

Practice Questions

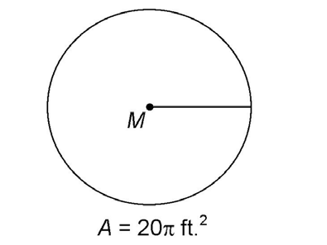
1. What is the radius of circle M?

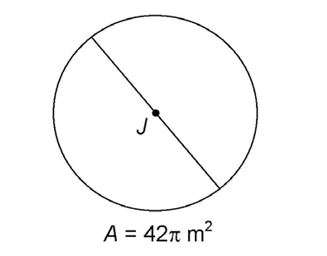
2. Find the diameter of circle J.

3. Circle Y has an area of 63 square yards. What is length of

Solutions

1. The radius measures 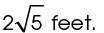The area of circle M is 20 square feet. Plug this into the area formula:

Now solve for r:

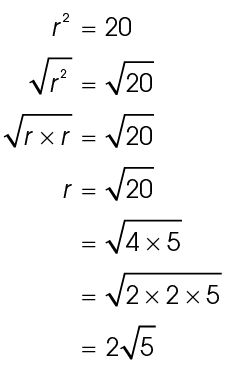
2. The diameter measures 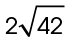meters.

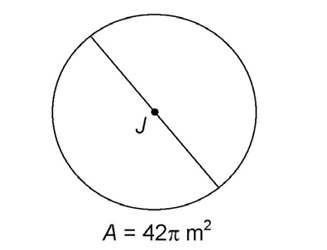
Start with the area formula:

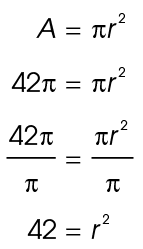
Next, solve for r:

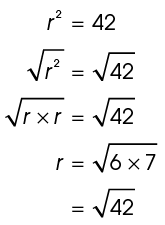
The number 42 cannot be broken down into any perfect squares, so we just leave 42 under the square root sign. The length of the diameter is twice the length of the radius. So, 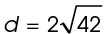meters.

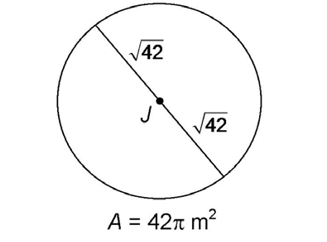
3. The length of 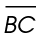is 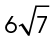yards.

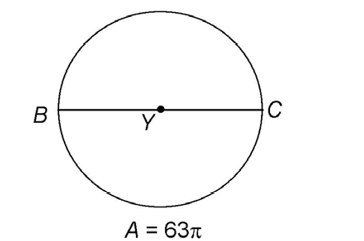
This question asks for the diameter of the circle. First find the radius, and multiply it by 2:

The radius is 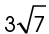yards. The diameter is twice this length, or yards.

Degrees in a circle

So far in this chapter, we’ve learned about the parts of a circle and how to find circumference and area. There are a few other important concepts to know about circles, but before we move on, let’s look at degrees.

We saw in the Angles chapter that a straight line measures 180°.

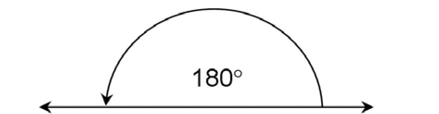
A circle measures 2 times 180, or 360°:

Arcs

A portion of the outer edge of a circle is known as an arc. The measure of an entire circle is 360°, but we sometimes need to know the measure of a part of the circle, too.

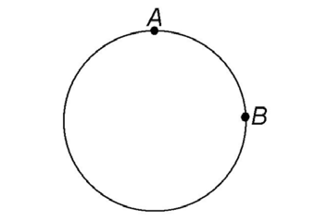
Arcs are commonly defined by two points on a circle. In this circle, there are two arcs between points A and B.

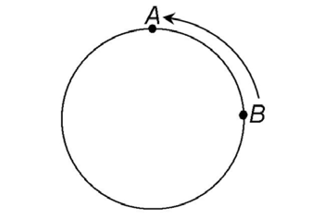
The smaller arc is known as the minor arc. It is shown by the arrow in the figure:

The larger arc is known as the major arc. To differentiate between the two arcs, a third point may be added to the circle:

We refer to the minor arc as arc AB. The major arc is labeled with three letters, ACB.

Arcs can be measured either in degrees or in units of length, such as inches, feet, or centimeters. When we refer to the measure of an arc, we are referring to its number of degrees. When we refer to the length of an arc, we are referring to how long it is in terms of inches or some other unit.

Central angles

The degree measure of an arc is equal to the measure of the central angle that intercepts the arc. A central angle of a circle is an angle that has its vertex at the origin, or center of the circle. Its sides are formed by two radii.

Examples

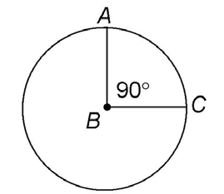
Angle ABC is a central angle of circle B. It measures 90°:

Since mABC = 90, this tells us that arc AC measures 90°.

In circle R below, 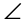QRS is a central angle that measures 45°. Its vertex is at the center of the circle, point R. Its sides are both radii of the circle.

Since QRS measures 45°, we know that arc SQ measures 45°.

Intercepted arcs

When a central angle intercepts the sides of a circle, it creates two arcs: a minor and a major one. We call the minor arc the intercepted arc of the central angle.

In circle B shown, minor arc AC is the intercepted arc of central angle ABC. Minor arc SQ is the intercepted arc of SRQ of circle R.

Practice questions

1. In the space below, draw circle L with central angle KLM that measures 60°.

2. In circle Z shown, what is the measure of arc WX?

3. In circle D shown, arc EF is the intercepted arc of central angle EDF. If arc EF measures 135°, what is the value of x?

Solutions

1. This circle shows central angle KLM, measuring 60°.

2. The measure of arc WX is 40°.

We are told that XZY is a right angle. So, we know that XZV also measures 90°. The measure of WZV is 50°, so WZX measures 90 – 50, or 40°. Arc WX is the intercepted arc of central angle WZX, so arc WX also measures 40°.

3. The value of x is 35°.

This question gives us an arc measurement and asks for the measure of a central angle. We are told that arc EF measures 135°. So, central angle EDF also measures 135°. Subtract the two given angles from 135 to find the value of x: 135° – 75° – 25° = 35°.

Sectors of circles

A central angle and its intercepted arc together make up what is known as a sector of a circle. A sector is a part of the circle in the shape of a wedge.

Examples

In circle B shown, sector ABC contains central angle ABC and intercepted arc AC. The central angle measures 90°, and arc AC also measures 90°.

Circle R contains sector SRQ, with central angle SRQ and intercepted arc SQ. The measure of SRQ is 45°, and the measure of is 45°.

You might be asked to find the area of a sector of a circle. To do this, you must determine what part of the circle the sector represents.

In circle B, sector ABC has a central angle of 90°. This central angle is equal to 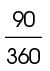of the entire circle, or 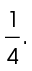Since the central angle represents one-fourth of the whole circle, sector ABC also represents one-fourth of the circle.

This relationship can be written as a proportion:

We can write it in math terms this way:

It can also be reduced, as follows:

You can reduce the fraction or not—it’s up to you. However, you may find the reduced fraction easier to work with.

Once we know the portion the sector makes up of the circle, we can find the area of the sector. Let’s say the radius of circle B is 8:

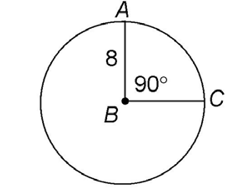
We can find the area of sector ABC by finding one-fourth the area of the entire circle. The area of the full circle is 64 square units:

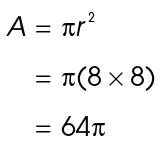
Set up a proportion to find the area of the sector:

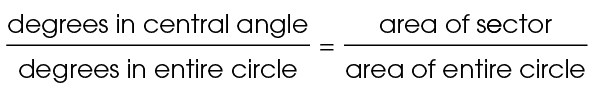
Substitute the values you know into the equation:

You might wish to reduce the fraction, as we saw above:

Now, solve for the area of the sector:

The area of sector ABC is 16 square units.

Practice Questions

1. Circle R has a radius of 2 centimeters, as shown in the figure. What is the area of sector SRQ?

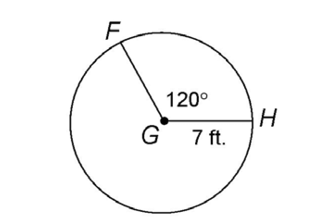
2. Circle G has a radius of 7 feet, as shown. Find the area of sector FGH.

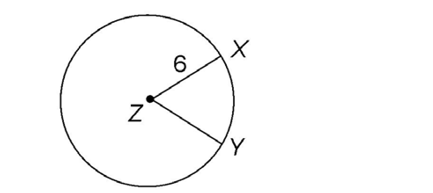
3. In circle Z shown, the area of sector XZY is 6 square units. What is the measure of central angle XZY?

Solutions

1. The area of sector SRQ is 0.5 square centimeters.

Circle R has a radius of 2 cm. Find the area of the full circle:

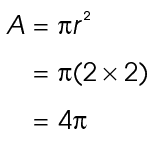
The area of the circle is 4 cm2. Next, find the ratio of the degrees in the central angle to the degrees in the full circle:

Set up a proportion to find the area of the sector:

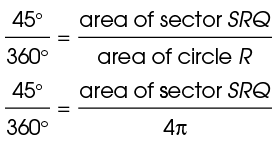
Cross-multiply to find the area of the sector:

2. The area of sector FGH is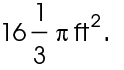

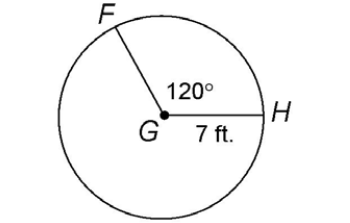
The circle has a radius of 7 feet. So, the area of the full circle is 49:

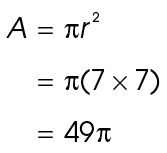
Next, determine what part the sector represents of the whole circle. The central angle measures 120°, and the full circle is 360°:

This can be further reduced to 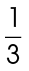. Thus, sector FGH is one-third of circle G.

Set up a proportion to find the area of the sector:

Cross-multiply to solve:

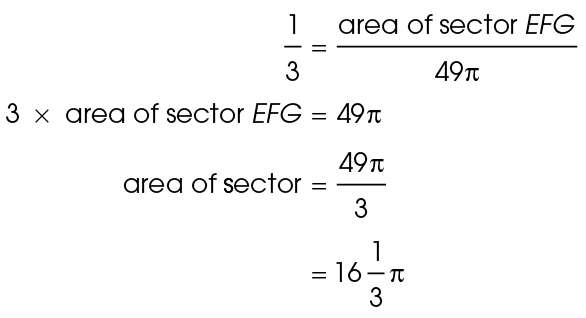
The area can also be written as approximately 16.33 square feet.

3. The measure of central angle XZY is 60°.

This question gives you the area of the sector, so you have to work backward to find the area of the central angle. Instead of setting up a proportion to find the area of the sector, set up the proportion to find the measure of the angle.

We are told that the area of sector XZY is 6 square units. Find the area of the entire circle:

The area of the full circle is 36 square units. So, the ratio of the area of the sector to the area of the full circle is

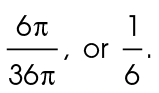
Set up a proportion to find the measure of the central angle:

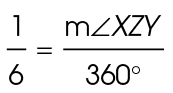
Solve for the measure of XZY:

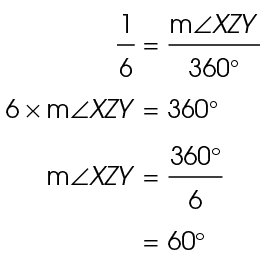
Arc length

In addition to finding the area of a sector, you may need to find its perimeter. This requires determining the arc length.

An arc represents a portion of the outer edge of the circle. If we know what portion of the circle the arc represents, we can calculate its length.

Examples

Circle C shown below has a radius of 5 meters. Central angle DCE intercepts arc DE and has a measure of 60°.

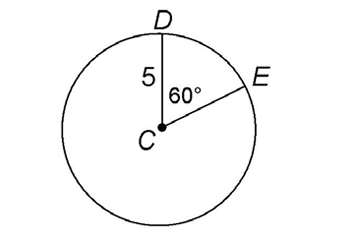
In degrees, the measure of arc DE is 60°. But we are looking for its measure in length—specifically, we want to know its number of meters.

To determine the length of the arc, we first determine the circumference of the full circle and the portion of the full circle that the arc represents. Then we can use a proportion.

The circumference of circle C is 2r, or 2 times times 5, which is 10 meters. The portion that the arc represents of the circle is the same as the ratio of the measure of the central angle to the measure of the full circle:

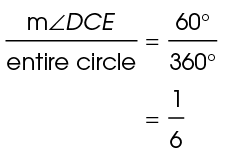
Arc DE represents one-sixth of the circle. Set up a proportion:

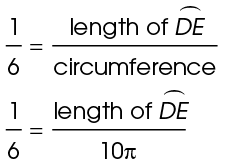
Solve the proportion to find the length of the arc:

Arc DE measures approximately 1.67 meters.

Finding sector perimeters

The perimeter of a sector can be found if we know the radius of the circle plus the length of the sector’s arc. In circle B, for example, the radius is 8 inches.

Both sides of the sector are radii of the circle. So, and both measure 8 inches. To find the length of first find the circumference of the circle:

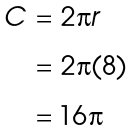
The circumference is 16 inches. Next, set up a proportion. Start with the ratio of the measure of the central angle to the measure of the full circle:

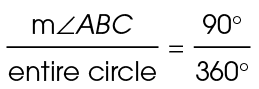
This ratio is the same as the ratio of the length of arc to the entire circumference. Set up a proportion with the two ratios:

Solve the proportion to find the length of the arc:

The length of arc AC is 4 inches. The perimeter of the sector is 8 + 8 + 4, or 16 + 4 inches.

Practice Questions

1. Circle T has a radius of 3 feet, as shown in the figure. Find the length of arc SU.

2. In the figure shown, circle O has a radius of 4.5 kilometers. What is the length of arc NP?

3. Circle O shown has an area of 81 square meters. The area of sector MON is 16.2 square meters. Find the perimeter of sector MON.

Solutions

1. The length of arc SU is 0.6 feet.

First, find the circumference of circle T. The circumference is 2r, or 6 feet.

Next, find the portion of circle T that arc SU represents. The measure of central angle STU is 36°. This represents 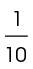of the circle:

Now, set up a proportion:

Cross-multiply to solve:

2. The length of arc NP is 0.3 kilometers.

The circumference of circle O is 2r, or 9 kilometers. Arc NP is intercepted by central angle NOP, which measures 12°. Central angle NOP represents 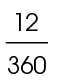of the circle, which reduces to of the circle. Set up a proportion and solve:

3. The perimeter of sector MON is 18 + 3.6 meters.

We are looking for the perimeter of sector MON. To find the perimeter, we must know the length of the radius and the length of

First, find the length of the radius. The area of circle O is 81 square meters. Plug this into the area formula and solve for r:

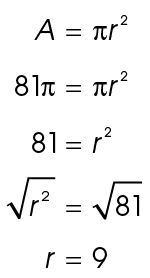
The radius, r, measures 9 meters:

Next, find the length of . To do this, we must find the circumference of the circle. We must also know what part of the circumference arc MN represents.

We are told that the area of circle O is 81 square meters, and the area of sector MON is 16.2 square meters. Set up a ratio with this information:

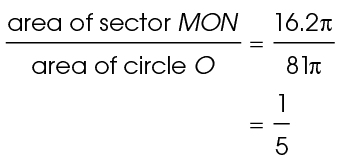
This tells us that sector MON is one-fifth of circle O.

Now find the circumference of the whole circle. The radius is 9 meters, so the circumference is 2r, or 18 meters. Arc MN is one-fifth of that, so the length of is 18 divided by 5, or 3.6 meters.

To find the perimeter of sector MON, add together the lengths of 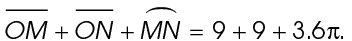The perimeter is 18 + 3.6 meters.

If we had been asked to find the degree measure of arc MN, we could divide the degree measure of the entire circle by 5. The degree measure of the arc is 360° divided by 5, which is 72°.

Inscribed angles

The last type of angle that we will look at in this chapter is the inscribed angle. Inscribed angles are angles with a vertex on the outer edge of the circle.

They are formed by two chords, which as we saw earlier are lines that extend between any two points on the outer edge of the circle.

Examples

In the circle shown, QRS is an inscribed angle measuring 40°. It intercepts arc QS. Chords RS and RQ are the sides of the angle.

To find the measure of an inscribed angle, use this formula:

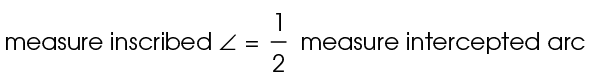
The intercepted arc of an inscribed angle is always twice the size of the angle itself. In the circle shown, QRS is 40°. That tells us that arc QS measures 80°.

Practice Questions

1. What is the measure of arc JL in the circle shown?

2. In the circle shown, inscribed angle UVW measures 55°. Find the measure of arc UW.

3. If the measure of arc XZ is 20° as shown, what is the measure of XYZ?

Solutions

1. The measure of arc JL is 48°.

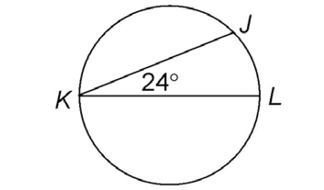
An intercepted arc is twice as large as the measure of its inscribed angle. Angle JKL measures 24°, so arc JL measures 48°.

2. The measure of arc UW is 110°.

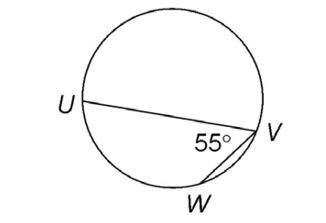
To find the measure of the arc, multiply the measure of the inscribed angle by 2. The arc measures 110°.

3. The measure of XYZ is 10°.

In this question, we are given the measure of arc XZ as 20°. Inscribed XYZ measures half this amount, or 10°.

Chapter Review

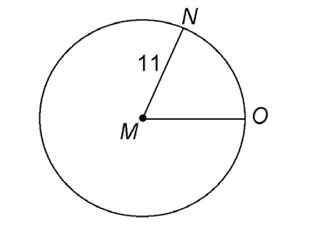
1. The radius TM of circle T measures 9. What is the length of diameter MN?

2. In circle M shown, what is the length of radius MO?

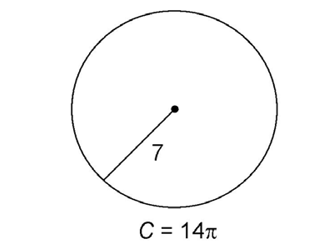
3. Find the circumference of circle R.

4. The circumference of this circle is 14. What is the length of its radius?

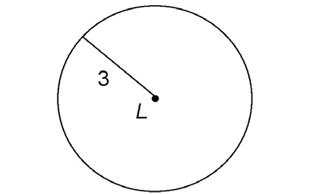
5. What is the area of circle L?

6. What is the radius of circle T?

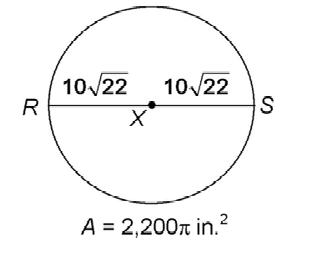
7. Circle X has an area of 2,200 square inches. What is length of ?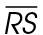

8. In circle O shown, what is the measure of 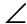POQ?

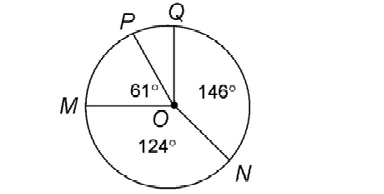
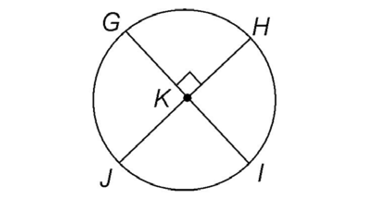
9. In circle K shown, what is the measure of arc HI?

10. Circle V has a radius of 30 units. What is the area of sector UVW?

11. In circle L shown, the area of sector KLM is 12 square inches. What is the measure of central angle KLM?

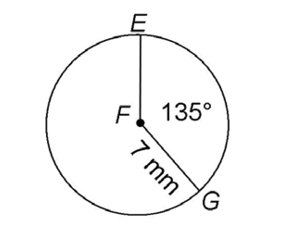
12. Circle Q shown has a circumference of 19 centimeters. What is the length, in centimeters, of arc RP?

13. What is the length of arc EG in circle F shown?

14. In the circle shown, inscribed angle TSR measures 15°. What is the measure of arc TR?

15. Intercepted arc HJ measures 130°, as shown in the figure. What is the measure of HIJ?

Solutions

1. The correct answer is shown below.

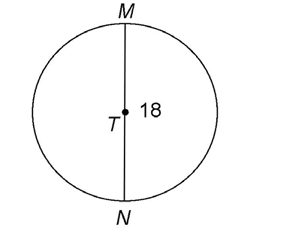
The diameter of a circle is twice the length of its radius. To find the length of diameter MN, multiply 2 × radius TM:

2 × 9 = diameter

2. Radius MN measures 11. Every radius on a circle has the same length. So, radius MO also measures 11.

3. To find the circumference, multiply 2 × radius × . The radius of circle R is 5. So, we multiply 2 × 5 × . The circumference is 10.

4. To find the radius, divide the circumference by 2. The circumference is 14, so we divide 14 by 2.

5. To find the area, multiply × radius × radius. The radius of circle L is 3. So, we multiply × 3 × 3.

6. The radius of circle T is

We are told that the area of the circle is 99. Substitute this into the area formula:

7. The length of 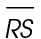is 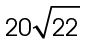inches.

First, find the length of the radius.

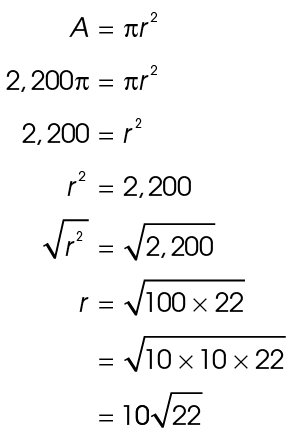
The radius is 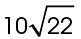inches, so the diameter is 2 times 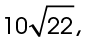or 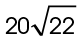inches.

8. The measure of POQ is 29°.

The number of degrees in an entire circle is 360°. The circle shown contains four central angles. The measures of three of the central angles are given; only POQ is missing. Subtract the measures of the three given angles from 360°: 360 – 124 – 146 – 61 = 29°.

9. The measure of arc HI is 90°.

We are shown that circle K is divided into four central angles by two diameters, The diameters are perpendicular, so all of the central angles are right angles. This means each of the four intercepted arcs also measures 90°.

10. The area of sector UVW is 50 square units.

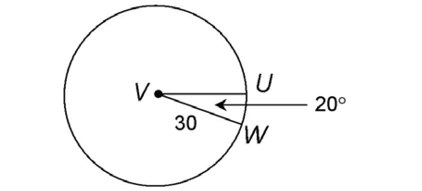
First, determine the ratio of the central angle to the full circle:

The sector is therefore 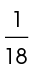of the full circle. Next, determine the area of the full circle. The area of the full circle is 900 square units:

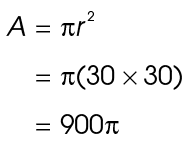
Now, set up a proportion to find the area of the sector:

Cross-multiply to solve:

The area of sector UVW is 50. We are not given any units of measurement, so we can just say 50 units2.

11. The measure of central angle KLM is 30°.

We are told that the area of sector KLM is 12 square inches. Using 12 for the radius, we can determine that the area of the circle is 144 square inches:

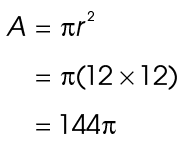
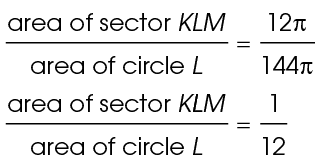
Find the ratio of the area of the sector to the area of the full circle:

Set up a proportion to find the measure of the central angle:

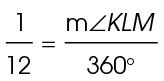
Solve for the measure of KLM:

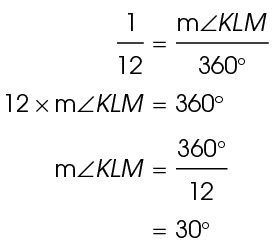
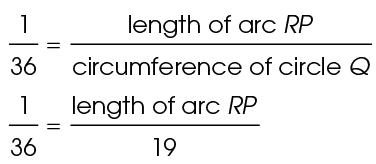
12. The length of arc RP is 0.53 centimeters.

To find the length of the arc, first find the portion of the circle that the arc represents. This arc is intercepted by central angle RQP, which measures 10°, so the arc also measures 10°. Set up a ratio:

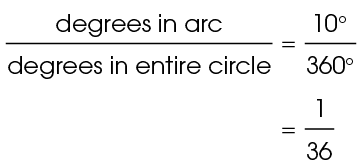
Arc RP represents 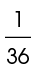of circle Q.

We are given the circumference of the circle, so we can use the ratio to create a proportion:

Cross-multiply to solve:

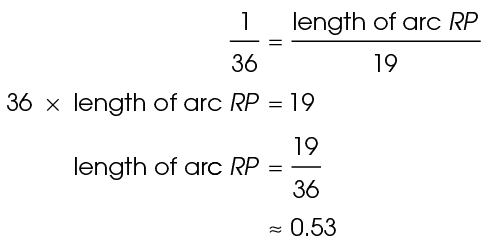
The circumference is given as 19 centimeters, without the symbol . This means that the value of has been figured into the circumference. So, we would give the length of the arc as approximately 0.53 centimeters.

13. The length of arc EG is 5.25 millimeters.

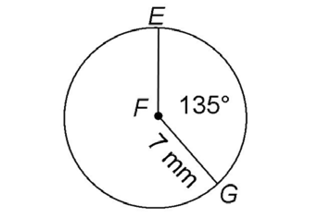
First, find the circumference of circle F. The circumference is 2r, or 14 millimeters. Next, find the portion of the circle that the arc represents. We are told that central angle EFG measures 135°:

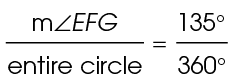
Use this ratio to create a proportion and solve:

Arc EG measures 5.25 millimeters.

14. Arc TR measures 30°.

The measure of an inscribed angle is exactly half the measure of its intercepted arc. In this figure, inscribed angle TSR measures 15°. Arc TR therefore measures 2 × 15, or 30°.

15. Inscribed 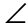HIJ measures 65°.

This circle contains an inscribed angle, HIJ, with intercepted arc HJ. We are given the measure of HJ, 130°. To find the measure of HIJ, calculate half the measure of its intercepted arc. In this case, the angle measures 130 divided by 2, or 65°.