Chapter 9

Irregular and Multiple Figures

Hi! I’m egghead. I will teach the following concepts in this chapter:

Irregular figures

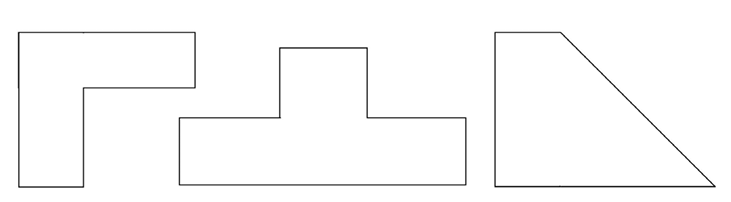
Irregular figures in geometry are those that do not have predictable properties like squares, rectangles, and other regular polygons do.

Here are some examples:

Finding perimeter

Finding the perimeter of irregular figures usually requires finding the lengths of some missing sides. To do this, it’s easier if you break the figures up into regular shapes.

Examples

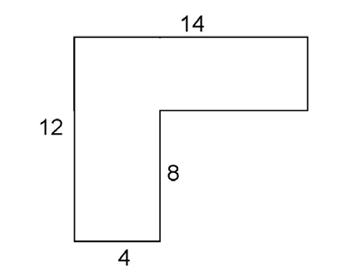
To find the perimeter of this figure, we just need to find the lengths of the missing sides. All of the angles are right angles.

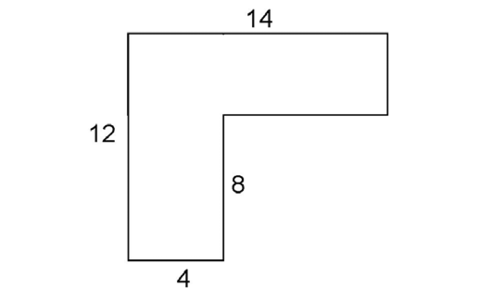
Use subtraction to determine the missing lengths: 12 – 8 = 4, and 14 – 4 = 10.

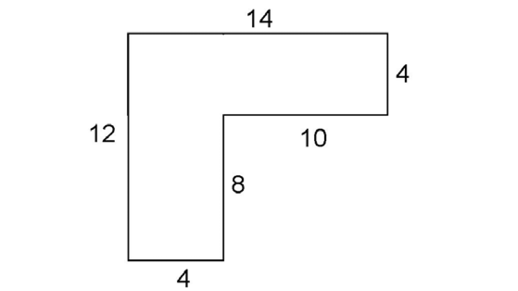
Next, add everything up. The perimeter is 12 + 4 + 8 + 10 + 4 + 14, which is 52.

Let’s try another example. This irregular figure has three missing sides. All of the angles are right angles.

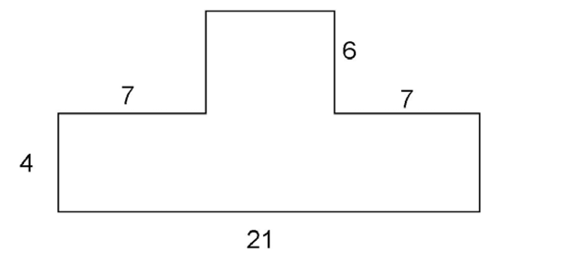
We can find the missing lengths using subtraction: 21 – 7 – 7 = 7. The other two missing sides are congruent to the sides labeled 4 and 6.

Next, add up the lengths of the sides:

21 + 4 + 7 + 6 + 7 + 6 + 7 + 4 = 62

The perimeter of the figure is 62.

Practice Questions

1. What is the perimeter of the figure shown?

2. Find the perimeter of the irregular quadrilateral shown.

3. A concrete skate park in the shape of a semi-circle has a diameter of 24 meters. A skater skates all the way around the outer edge of the park. How many meters does the skater travel?

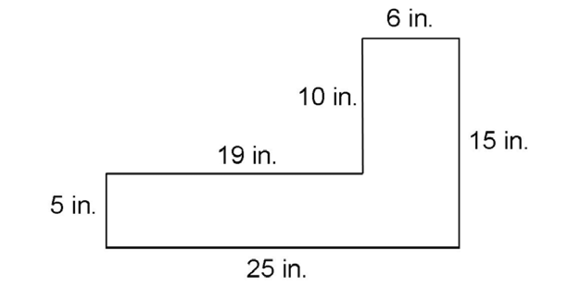
4. A building contractor gets a new job to finish a staircase. He has to figure out the perimeter of the staircase already built to build a replica. All intersecting lines meet at right angles, as shown. What’s the perimeter of the staircase?

5. Find the perimeter of the figure shown.

Solutions

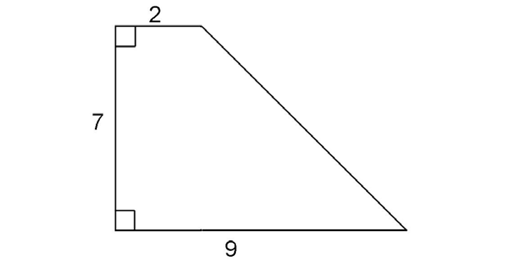
1. The perimeter of the figure is .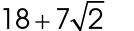

Divide the figure into a rectangle and a triangle. The rectangle has a length of 7 and a width of 2. The triangle has two legs that measure 7. So, the two angles opposite these legs are equal, and they measure 45°.

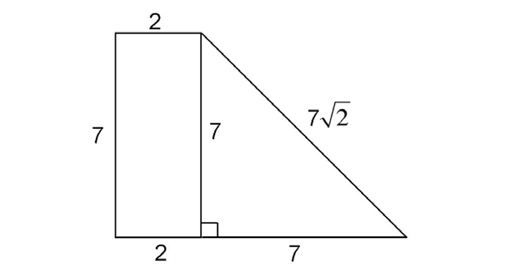
This is a 45-45-90 triangle, with side lengths in a ratio of 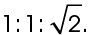If two legs measure 7, the hypotenuse must measure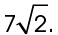

Add up the lengths of the sides to find the perimeter: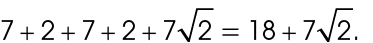

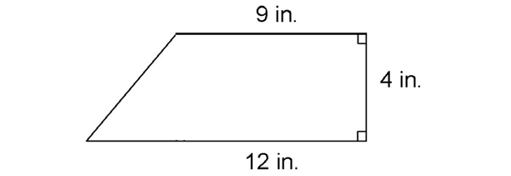
2. The perimeter of the figure is 30 inches.

Divide the figure into regular shapes that you can work with easily. If we draw a perpendicular line as shown, the figure divides into a triangle and a rectangle.

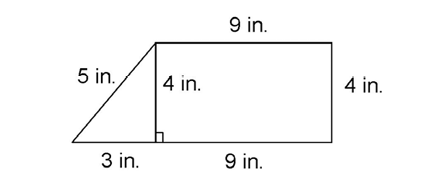
The perpendicular line has length 4 inches. The bottom of the figure separates into 9 inches and 3 inches, as shown. This shows us we have a 3-4-5 right triangle. The hypotenuse measures 5 inches.

Adding up the lengths of the sides, we find the perimeter measures 9 + 4 + 9 + 3 + 5, or 30 inches.

3. The skater travels a total of 12 + 24 meters.

The diameter of the semi-circle is 24 meters. The radius measures half this length, or 12 meters.

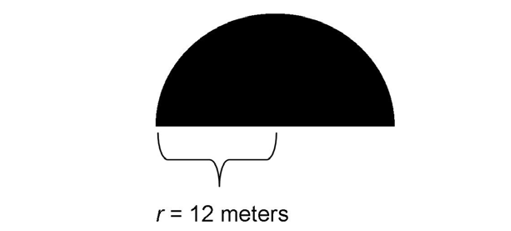
To find the circumference of the semi-circle, we calculate half the circumference of the full circle. A circle with radius 12 meters has a circumference of 2 times times 12, or 24 meters. We want the circumference of the semi-circle, so we take half of 24 meters. The circumference of the semi-circle is 12 meters.

The skater travels not just along the curved edge of the semi-circle, but along the straight edge too. The total distance traveled is 12 + 24 meters.

4.

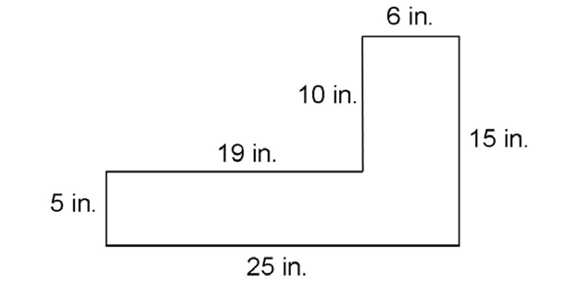
First, determine the length of the missing sides. Then add the side lengths to obtain the perimeter.

To find the lengths of the missing sides, use subtraction. For the horizontal side, subtract 25 – 6. The missing horizontal side measures 19 inches. For the vertical side, subtract 15 – 5. The missing vertical side measures 10 inches.

Now add up the lengths of the sides: 25 + 5 + 19 + 10 + 6 + 15 = 80. The perimeter of the figure is 80 inches.

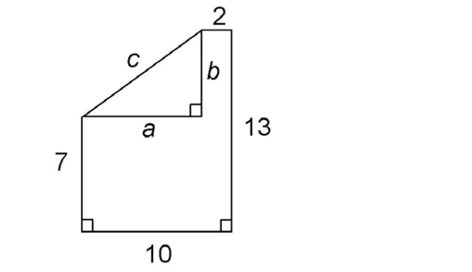
5. The figure contains a right triangle with sides labeled a, b, and c. To find the perimeter of the shape, we must determine the length of c.

We can find the lengths of a and b using subtraction. The horizontal leg, a, measures 10 – 2 = 8 inches. The vertical leg, b, measures 13 – 7 = 6 inches. Mark these on the figure as shown:

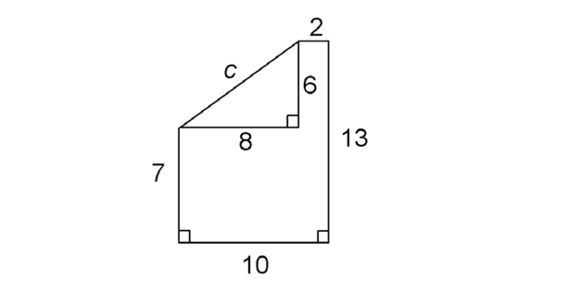
The right triangle has two legs measuring 6 and 8, so it is a 6-8-10 Pythagorean triple. The hypotenuse, c, measures 10.

Add up the lengths of the sides of the figure: 10 + 2 + 13 + 10 + 7 = 42. The perimeter is 42 units.

Finding area

To find the area of irregular figures, again it helps to divide the figure into regular shapes. We find the area of each shape, and add the areas together.

Examples

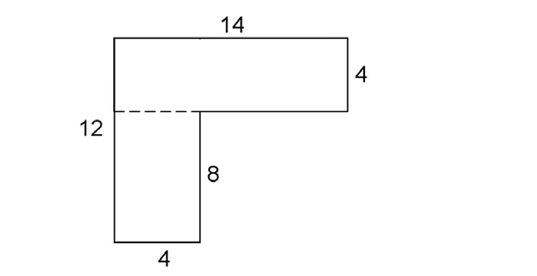
Here is a figure that we saw in the section on perimeters above. All lines meet at right angles.

We can find the area by dividing the figure into two rectangles. The upper rectangle has an area of 14 × 4 = 56 square units. The lower rectangle has an area of 8 × 4 = 32 square units. The area of the figure is 56 + 32 = 88 units2.

Here is a second example. Again in this figure, all angles are right angles.

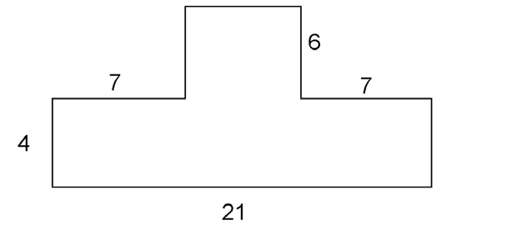
This figure can also be divided into two rectangles.

We can then find the area of the rectangles and add them up. The top rectangle has an area of 7 × 6 = 42 units 2. The bottom rectangle has an area of 4 × 21 = 84 units 2. The total area is 126 square units.

Practice Questions

1. What is the area of the figure shown?

2. Find the area of the irregular quadrilateral shown.

3. What is the area of the concrete skate park shown in the figure?

4. Find the area of the figure below.

5. Find the area of the figure below.

Solutions

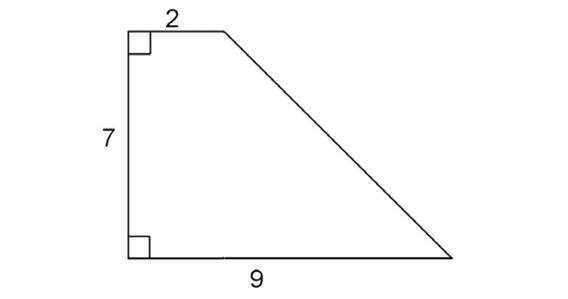
1. The area of the figure is 38.50 square units.

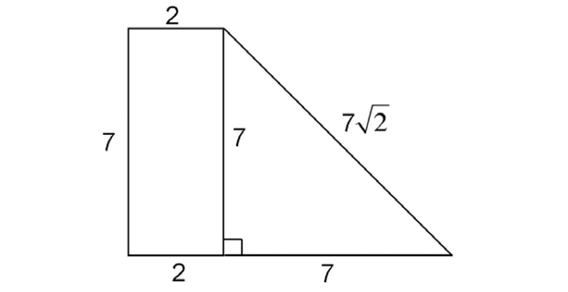
By dividing the figure into a rectangle and a triangle, we can find the lengths of the missing sides. The rectangle has an area of 7 times 2, or 14 square units. The triangle has an area of 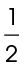times 7 times 7, or 24.50 square units. Added together, these areas give us a total of 38.50 units2.

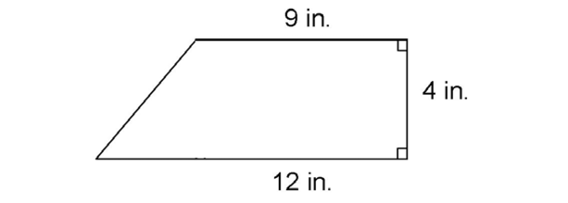
2. The area of the figure is 42 in2.

The figure divides into a triangle and a rectangle. The rectangle has an area of 4 times 9, or 36 square inches. The triangle has an area of 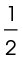times 3 times 4, or 6 square inches. The total area is 36 + 6 = 42 in2.

3. The area of the skate park is 72 square meters.

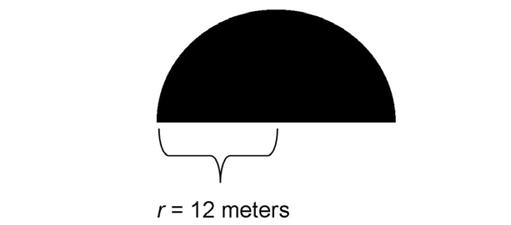
The skate park has a diameter of 24 meters and a radius of 12 meters. To find the area of a circle, we calculate times r times r, which in this case is times 12 times 12, or 144.

Don’t stop there, however! The question asks for the area of the semi-circle, which is half of that value. The area of the park is 72 m 2.

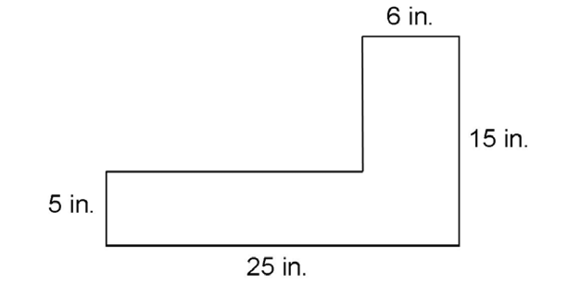
4. The area is 185 square inches.

First, find the lengths of the missing sides. The missing horizontal side is 25 – 6, or 19 inches. The missing vertical size measures 15 – 5 = 10 inches.

Next, divide the figure into two rectangles. Two possible rectangles are shown by the dotted line:

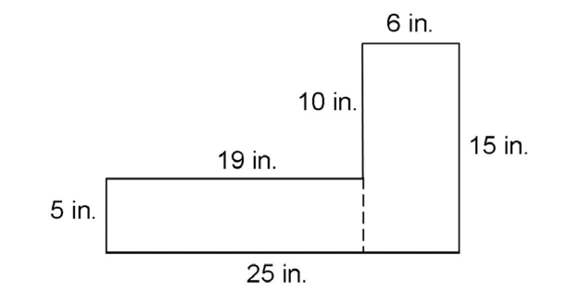
One rectangle measures 19 by 5 inches, and the other measures 6 by 15 inches. Calculate the area of both rectangles: 19 × 5 = 95 square inches, and 6 × 15 = 90 square inches. Added together, this gives a total area of 95 + 90 = 185 square inches.

5. The area of the figure is 345 square meters.

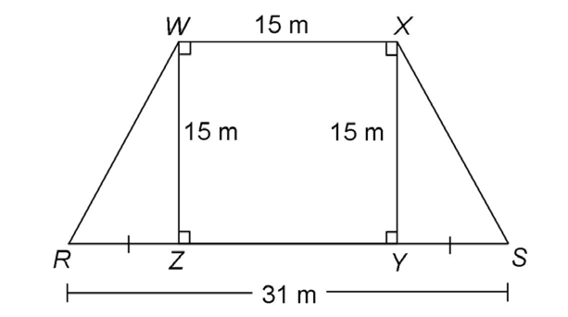
This figure contains a square, WXYZ, and two right triangles.

To find the total area, we must determine the area of the square plus the area of the two triangles. The area of the square equals 15 × 15, or 225 square inches.

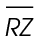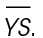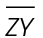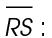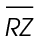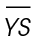To find the area of the triangles, we must find the lengths of bases and The length of line segment RS is given as 31 meters. Subtract the length of side from side 31 – 15 = 16 meters. Since and are congruent, we can divide 16 by 2 to get the measure of each: 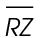and 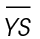each measure 8 meters.

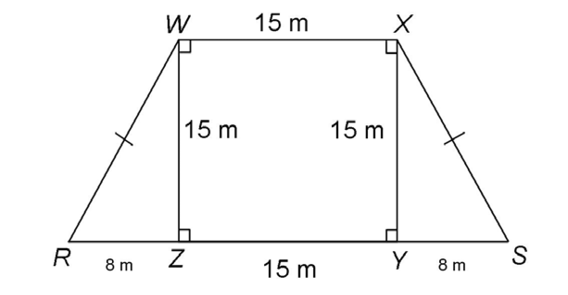
Now, determine the area of each triangle:

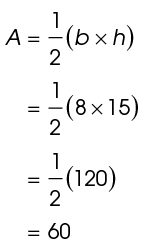
The area of each triangle is 60 square meters. Add together the three areas: 60 + 225 + 60 = 345. The area of the figure is 345 square meters.

Rules of diagonals

Before we move on to multiple figures, there are some properties of diagonals that are helpful to know. A diagonal is a straight line drawn from one corner of a polygon to another corner that is not adjacent.

Here is one diagonal of a rectangle:

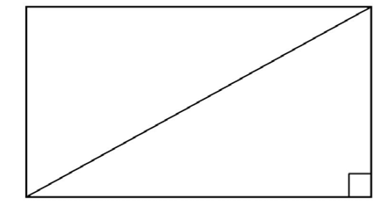
Diagonals commonly appear on geometry test problems, particularly those problems that involve quadrilaterals. The diagonals of each shape have different properties.

Parallelograms

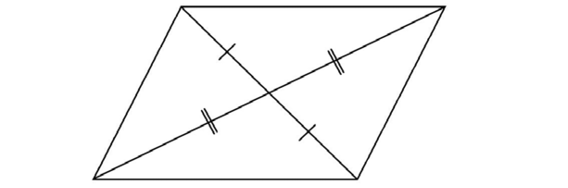
The diagonals of a parallelogram bisect each other.

Each diagonal is divided into two equal parts, but the diagonals are not congruent.

Rectangles

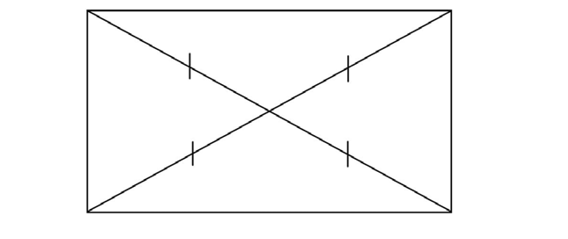
The diagonals of a rectangle bisect each other. They are also congruent.

Rhombuses

The diagonals of a rhombus bisect each other. They are also perpendicular.

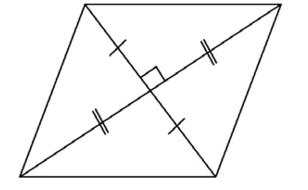
They also bisect the interior angles of the rhombus:

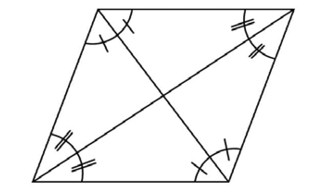
However, they are not congruent.

Parallelograms and rhombuses are slanted, so one diagonal is longer.

Squares

Squares have the properties of both rhombuses and rectangles.

The diagonals of a square bisect each other and are congruent. They are perpendicular, and they bisect the interior angles of the square.

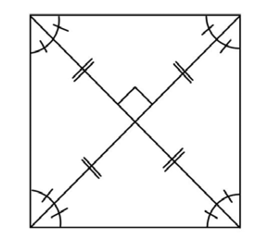
In fact, because we know that squares have four right angles, we can tell the exact measurement of the angles that are formed when the diagonals are drawn in:

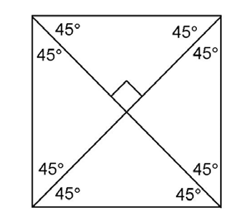
Trapezoids

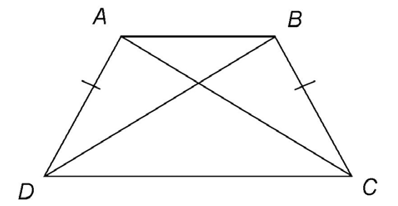
Trapezoids don’t have many diagonal rules. For an isosceles trapezoid, diagonals are congruent. No other types of trapezoids have special diagonal properties.

Multiple figures

Along with problems involving irregular figures, some geometry exams contain questions about multiple figures. Like with irregular figures, multiple figures can be highly varied.

Two triangles

One common type of multiple figures question concerns two triangles that are connected in some way. The triangles may be drawn inside a figure or joined by shared angles or sides.

Examples

Here are some examples. This figure highlights two sets of two triangles created when diagonals are drawn in a rhombus:

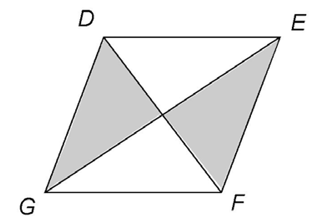
This figure has two triangles joined at a single point:

Two triangles can also be created by a single diagonal drawn in a rectangle or other quadrilateral:

With questions involving two triangles, it’s always helpful to look for the special right triangles, such as 30-60-90 triangles, 45-45-90 triangles, and Pythagorean triples.

Inscribed figures

Geometry questions also contain figures that are drawn inside other figures. We call these inscribed figures.

Examples

Inscribed figures can have a great degree of variation. Here is a triangle drawn within a square:

We might also have a quadrilateral within a triangle:

Other possibilities are triangles within circles, circles inside triangles, circles inside squares, and squares inside circles:

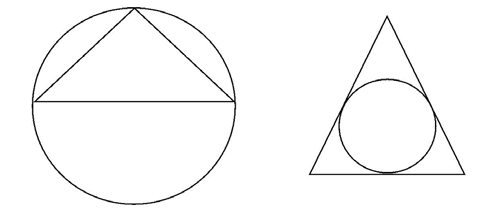
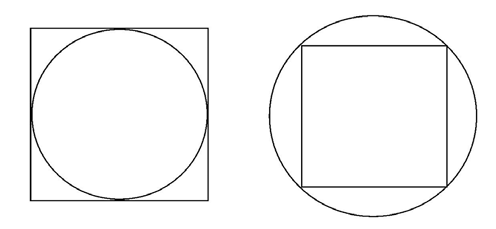
There are many possible multiple-figure combinations. To answer questions about them, draw on the properties of the shapes you know.

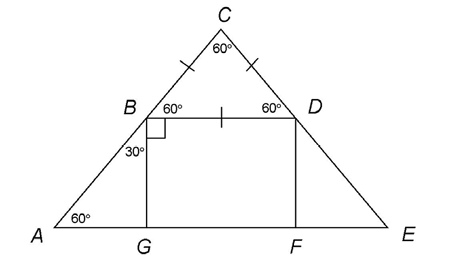
In the figure shown, BDFG is a rectangle and CBD is equilateral. What is the measure of BAG?

The measure of BAG can be found by applying the properties of certain triangles. First, equilateral triangles have three equal angles and three equal sides. All angles measure 60°. Draw these into the figure, as shown.

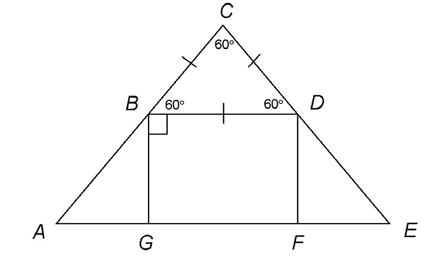
Next, we can find the value of 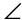ABG by using the properties of straight lines. Every straight line measures 180°. The angles that form a straight line are supplementary. So, 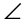CBD, 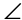DBG, and 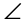ABG are supplementary. This can help us find the value of 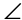ABG:

Knowing that ABG measures 30°, we can determine the value of BAG: 180 – 90 – 30 = 60°.

Practice Questions

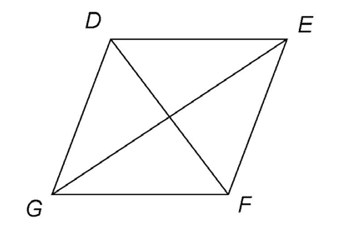
1. If DF = 6 and GE = 8, what is the perimeter of the rhombus shown?

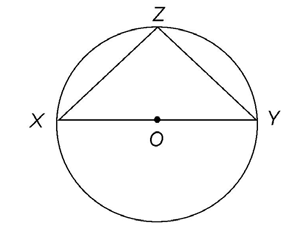
2. Triangle XZY is inscribed in a circle with center O. If the base of the triangle measures 4 yards, what is the radius of circle O?

3. A circle with center Z is inscribed in a square, as shown. If the sides of the square each measure 10 inches, what is the area of circle Z?

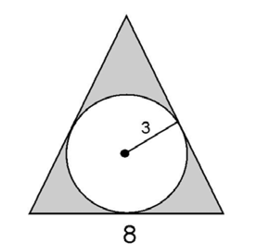
4. The height of the triangle shown in the figure is 14. What is the area of the shaded portion of the figure, to the nearest two decimal places?

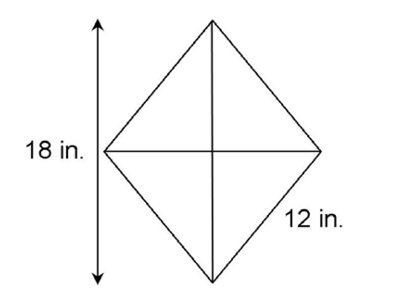
5. The rhombus shown has side lengths measuring 12 inches. It is divided into four triangles by its two diagonals. If the longest diagonal measures 18 inches, what is the area of one of the triangles?

Solutions

1. The perimeter of the rhombus is 20.

This rhombus has one diagonal measuring 6 and another measuring 8. The diagonals of a rhombus bisect each other at right angles. They form four right triangles, as shown:

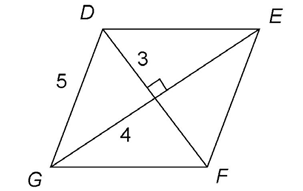
Since DF = 6, the leg of one triangle is 3. And since GE = 8, the other leg of the triangle is 4. This is a 3-4-5 triangle, with a hypotenuse measuring 5. The hypotenuse is the side of the rhombus, so the perimeter of the rhombus is 5 + 5 + 5 + 5, or 20.

2. The radius of circle O is 2 yards.

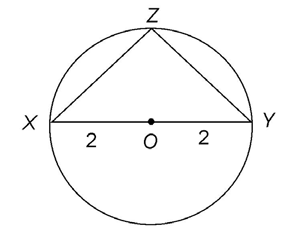
Here we are told that XY = 4 yards. The base of the triangle runs through the center of the circle, O. So, the base of the triangle is a diameter of the circle. The radius equals half the length of the diameter. This means the radius measures 2 yards.

3. The area of circle Z is 25 square inches.

We are told that the sides of the square measure 10 inches. The diameter of circle Z is the same length as the side of the square. The diameter of circle Z therefore measures 10 inches, and the radius measures 5.

Use the formula for the area of a circle:

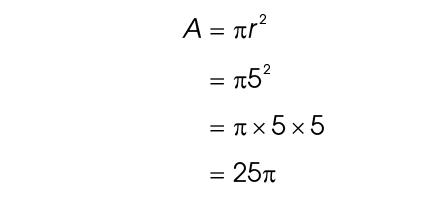
The area of the circle is 25 in2.

4. The area of the shaded portion of the figure is approximately 27.74 square units.

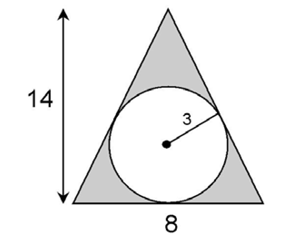
Subtract the area of the circle from the area of the full triangle. This will leave us with the area of the shaded portion of the figure.

The base of the triangle is 8 units, and the height is 14. The area of the entire triangle is 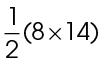, or 56 square units. The area of the circle is × 32, or 9 square units. The area of the shaded portion is 56 – 9, or approximately 27.74 square units.

5. The area of one triangle is 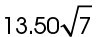square inches.

To find the area of one triangle, we must know its base and height. According to the rules of diagonals, the diagonals of a rhombus bisect each other. The longest diagonal is 18 inches, so half of this is 9 inches. We can mark this on the figure as the height of one of the triangles. We have marked the base of the triangle b:

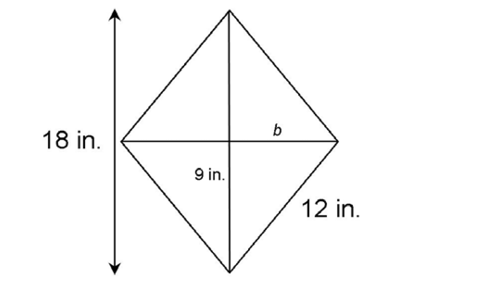
To find the length of b, use the Pythagorean theorem:

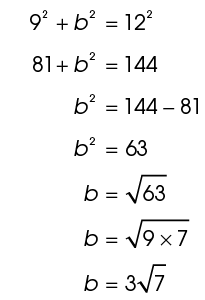
The length of b is 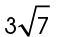inches.

Substitute the values of b and h into the formula for the area of a triangle:

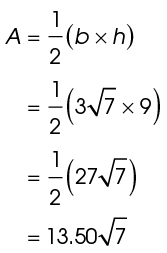
The area of one triangle is 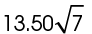square inches.

Chapter Review

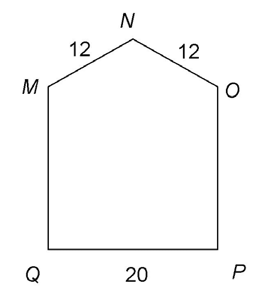
1. In the figure below, quadrilateral MOPQ is a square. What is the perimeter of MNOPQ?

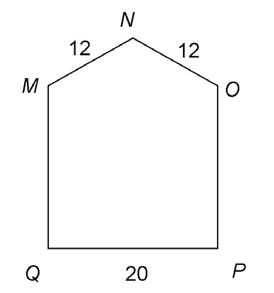
2. In the figure below, quadrilateral MOPQ is a square. What is the area, in square units, of pentagon MNOPQ?

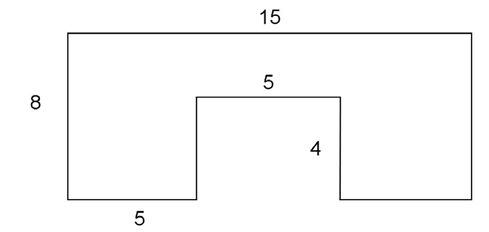
3. What is the area, in square units, of the figure shown? All angles in the figure are right angles.

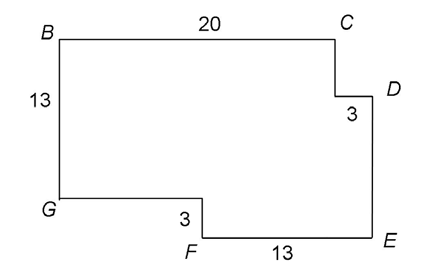
4. The map below shows a downtown shopping district. Six stores in the district are labeled B, C, D, E, F, and G. The numbers on the figure represent the number of blocks between each store. All of the corners are right angles.

Bonnie starts at store B and walks to store E. Assuming she must use one of the routes shown in the figure below, what is the minimum number of blocks Bonnie must walk to reach store E?

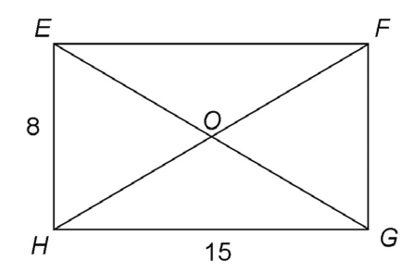
5. Rectangle EFGH has a length of 15 meters and a width of 8 meters, as shown in the figure. What is the perimeter of OHG?

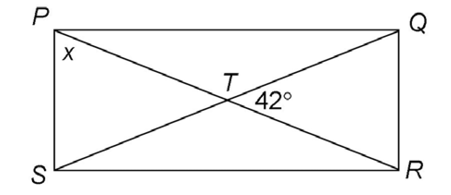
6. Rectangle PQRS has diagonals that intersect at point T, as shown. What is the measure of x?

7. In the figure shown, what is the value of a?

8. If AD = 6 inches, what is the length of diagonal 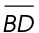in the rectangle shown?

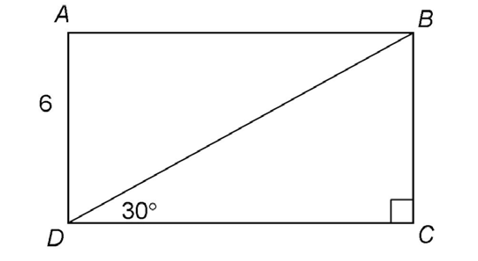
9. A rectangular swimming pool is surrounded by a brick walkway that measures 2 feet in width. The outer dimensions of the walkway are 40 feet by 52 feet as shown. What is the area of the swimming pool?

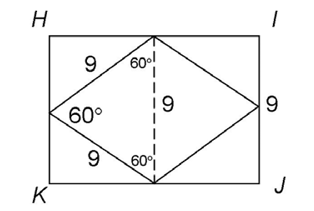
10. A rhombus is inscribed in rectangle HIJK, as shown in the figure. What is the measure of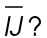

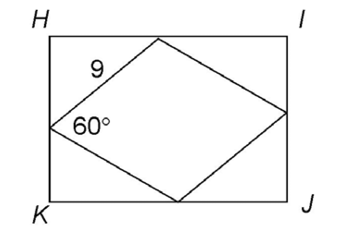
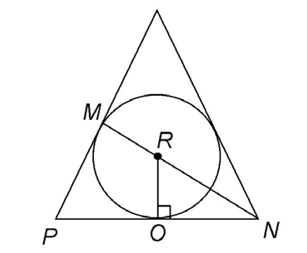
11. A circle with center R is inscribed in a triangle, as shown. Line segment bisects the base of the triangle at point O. If PN = 8 feet, and RN = 5 feet, what is the area of circle R?

12. Right triangle RST is inscribed in circle T as shown. What is the value of z?

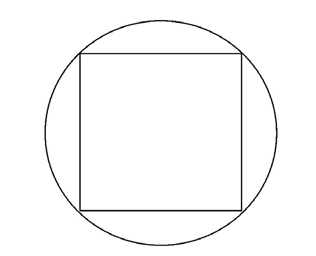
13. A square is inscribed in a circle as shown. If the sides of the square measure 12 units, what is the measure of the diameter of the circle?

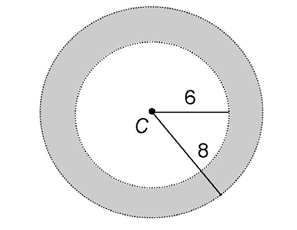
14. A circular garden with its center at point C contains an inner and outer portion, as shown in the figure. What is the area of the shaded part of the garden?

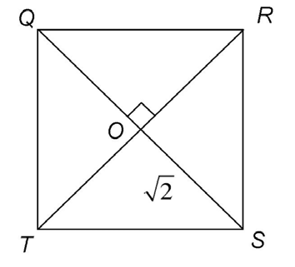
15. In the figure shown, QRST is a square with diagonals that meet at point O. The length of 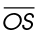is 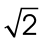centimeters. What is the perimeter of QRST?

Solutions

1. The perimeter of MNOPQ is 84.

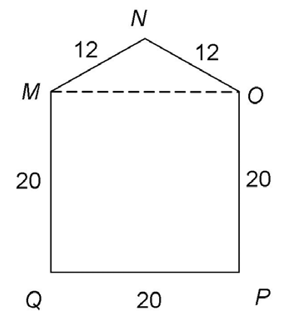
Determine the lengths of the missing sides. MOPQ is a square, so each side measures 20. The perimeter of the pentagon MNOPQ is 20 + 20 + 20 + 12 + 12, which equals 84.

2. The area of pentagon MNOPQ is 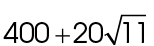square units.

To find the area of the figure, we first draw in the lengths of the missing sides.

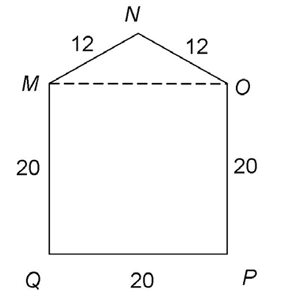
The figure can be divided into triangle MNO and square MOPQ. Find the area of these two shapes and add them together.

The area of MOPQ is 20 times 20, or 400. The area of MNO is 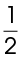the base times the height of the triangle. To find the base and height, draw a perpendicular line from point N to the middle of 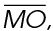as shown. We have labeled the perpendicular 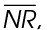as shown. The perpendicular bisects 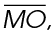so the base of the triangle MNR measures 10.

The height of the triangle is 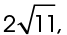and the base is 20. Use the formula for the area of a triangle:

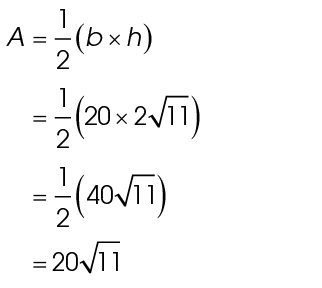
The area of the triangle is 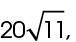and the area of the square is 400. The area of pentagon MNOPQ is 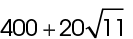square units.

3. The area of the figure is 100 square units.

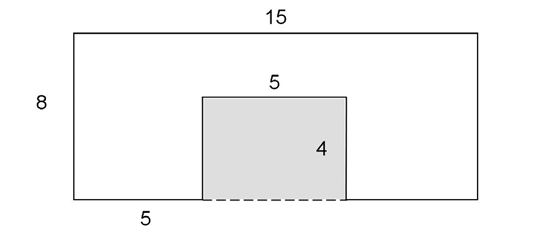
This figure contains a smaller rectangle inside a larger one. The smaller rectangle is shaded in the figure shown.

To find the area of the white part of the figure, subtract the area of the shaded rectangle from the area of the larger one. The area of the larger rectangle is 8 times 15, or 120 square units. The area of the shaded rectangle is 5 times 4, or 20 square units. The area of the larger rectangle minus the shaded portion is 120 – 20, or 100 units2.

4. To walk from store B to store E using one of the routes shown, Bonnie must walk 39 blocks.

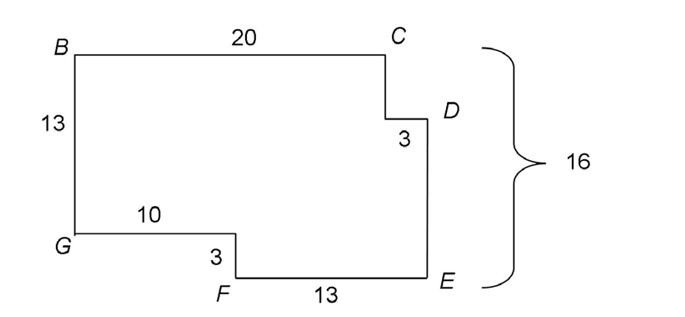
First, find the lengths of the missing sides. We know that the missing side between G and F measures 10 blocks, because there are 23 blocks in an east direction between building B and building D. Subtract the length of from 23 to find the missing length at the bottom of the figure: 23 – 13 = 10 blocks.

The distance from building C to building E is 16 blocks. We know this because there are 13 blocks between building B and building G. Building F is an additional 3 blocks farther south.

Bonnie could walk one of two routes. First, she could walk east from building B to building C and then south and east to building D and straight south to building E. This would be a total of 20 + 3 + 16, or 39 blocks. Alternatively, she could walk south 13 blocks from building B to building G, then 10 blocks east and another 3 blocks south to building F, followed by 13 blocks east from building F to building E. That route would be 13 + 10 + 3 + 13, or 39 blocks as well. Either way, Bonnie would walk 39 blocks.

5. The perimeter of OHG is 32 meters.

Triangle EGH is a right triangle with two legs measuring 8 and 15 meters. Therefore, it is a special right triangle—one of the Pythagorean triples. Its sides measure 8, 15, and 17.

The length of hypotenuse is 17 meters. So, the length of each missing side of the triangle is half of 17, or 8.5 meters. The perimeter of 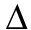OHG is 8.5 + 8.5 + 15 = 32 meters.

6. The measure of s is 69°.

The diagonals create two sets of vertical angles. The measure of 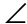QTR is 42°, and 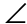PTS is equal to 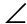QTR. So, PTS also measures 42°.

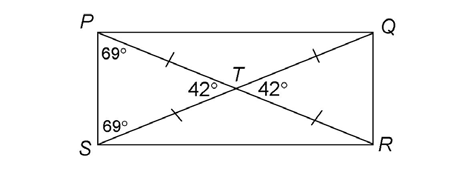
Using the rules of diagonals, we know that and bisect each other. This tells us that 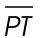is congruent to 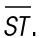The triangle PTS is isosceles, and 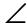TPS is congruent to 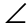TSP.

The triangle has two equal angles plus another that measures 42°. The three angles must add up to 180°. Use subtraction to find the value of x:

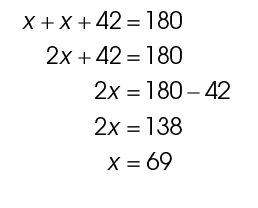
7. The value of a is 36°.

The figure shows that one angle measures 72°. The triangle is isosceles, so it has two equal angles. Since two angles measure 72°, subtract these from 180° to find the value of the third: 180 – 72 – 72 = 36.

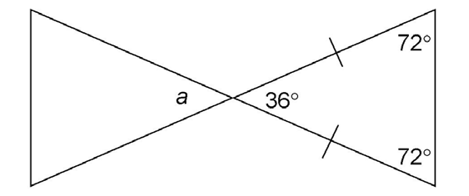
The 36° angle is a vertical angle with the angle labeled a. So, 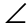a also measures 36°.

8. The length of 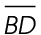is 12 inches.

The rectangle contains two right triangles. Both are 30-60-90 triangles. If BDC measures 30°, then the measure of ADB must be 60°. This means ABD measures 30°.

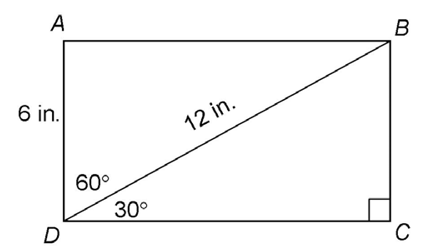
Once we know that this is a special right triangle, we can use its properties to determine the lengths of its sides. The sides of a 30-60-90 triangle are in a ratio of 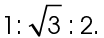The side across from the 30° angle is the smallest side; in this case, AD = 6 inches. Therefore, the hypotenuse 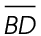must measure 2 times 6, or 12 inches.

9. The area of the swimming pool is 1,728 square feet.

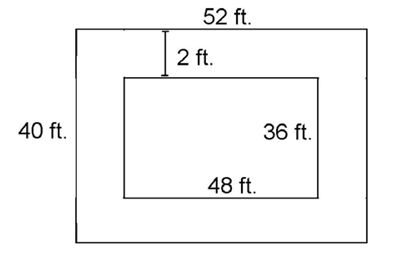
The outer dimensions of the walkway are 40 feet by 52 feet. The walkway measures 2 feet in width, so subtract to find the width of the pool: 40 feet – 2 feet – 2 feet = 36 feet in width, and 52 feet – 2 feet – 2 feet = 48 feet in length. The dimensions of the pool are 36 feet by 48 feet. Its area is 36 times 48, or 1,728 square feet.

10. The measure of 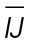is 9.

We are shown one angle in the figure that measures 60°. Draw a line through the middle of the rhombus to create two triangles.

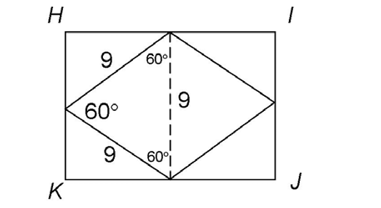
A rhombus has four congruent sides, so we know all sides measure 9. This means that the three angles of the triangle are equal. If the known angle measures 60°, and the remaining two angles are equal, they must measure 60° too.

The triangle is an equilateral triangle, with three equal angles and three equal sides. The side marked with the dotted line must measure 9. This means side is also 9 units in length.

11. The area of circle R is 9 square feet.

Line segment bisects the base of the triangle, which measures 8 feet. This tells us that ON = 4 feet. We’re also told that RN = 5 feet.

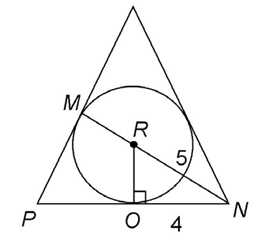
Notice that triangle RNO has two sides that measure 4 and 5 feet. The hypotenuse, is the side that measures 5. Therefore, this is a 3-4-5 Pythagorean triple. The remaining side must measure 3 feet:

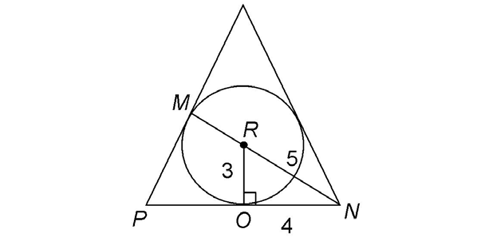
We now know the radius of circle R is 3 feet. Using this information, find the area of the circle:

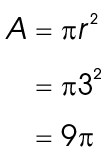
12. The measure of z is 45°.

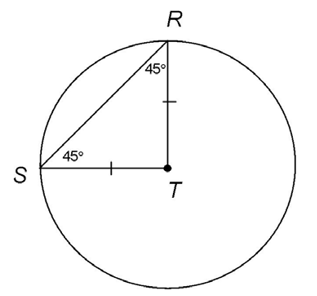
Circle T contains an inscribed triangle, RTS. The measure of T is 90 degrees. The two legs of the triangle are congruent, because they are both radii of the circle. Therefore, mS ≅ m 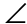R. Since the two angles add up to 90°, they each measure 45°.

13. The diameter of the circle measures 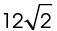units.

The square has sides that measure 12 units. Draw in the lengths of the sides and the diameter of the circle:

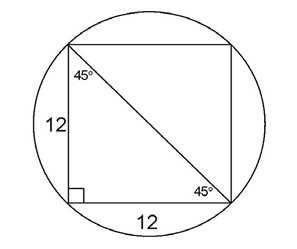
The diameter of the circle is also a diagonal of the inscribed square. According to the rules of diagonals, the diagonals of a square bisect the angles of the square. Therefore, the angles measure 45°, as shown.

We now have a 45-45-90 triangle, with sides in a ratio of 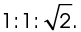Since the legs of the triangle measure 12 units, the hypotenuse must measure 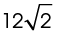units.

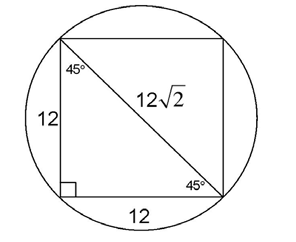
14. The shaded part of the garden has an area of 28 square units.

The area of the entire outer garden is times 82, or 64. The area of the inner garden is times 62, or 36. Subtract the area of the inner garden from the area of the entire outer garden to get the area of the shaded portion: 64 – 36 = 28 units2.

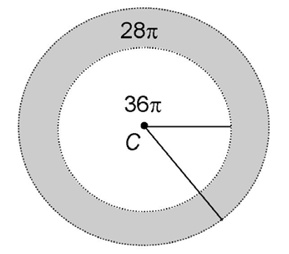
15. The perimeter of QRST is 8 centimeters.

To find the perimeter of QRST, we must know the length of one side. This is possible if we recognize that the diagonals create special right triangles.

The rules of diagonals for squares state that the diagonals bisect the angles of the square. So, the diagonals create 8 angles each measuring 45 degrees:

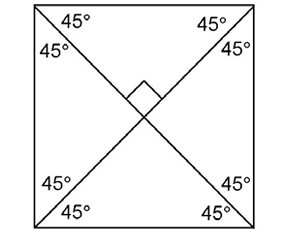
Therefore, we know that RSO is a 45-45-90 triangle. It has two congruent legs, as shown:

The sides of a 45-45-90 triangle are in the ratio 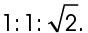If the two legs measure 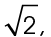then the hypotenuse must measure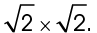

Multiply the two square roots:

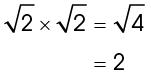
The length of the hypotenuse is 2 centimeters.

Add up the lengths of the sides to find the perimeter: 2 + 2 + 2 + 2 = 8.

We’ve covered a lot of ground with 2-D shapes so far. Next, we’ll move on to shapes in three dimensions.