© Karan Singh Garewal 2020

K. S. GarewalPractical Blockchains and Cryptocurrencieshttps://doi.org/10.1007/978-1-4842-5893-4_10

10. Merkle Trees

Karan Singh Garewal¹ 

(1)

Toronto, ON, Canada

 

In the last chapter, we engaged in a comprehensive examination of cryptocurrency transactions. Transactions are the fundamental unit of computation in cryptocurrency networks. Without transactions, there is no blockchain. A block consists of several transactions as well as related data. For any block that contains transactions, we want to ascertain two properties: firstly, that these transactions have not been tampered with and, secondly, whether a particular transaction is present in the block.

You will recall from Chapter 8 that the block attribute prevblockhash is used to test whether the previous block has been tampered with. This hash is computed over the block header of the previous block. The transactions in the previous block are not in this block header. However, the block header contains the merkle root of these transactions. This root can be used to verify the integrity of the transactions in the block. If any of the transactions have been altered, the merkle root will change, and consequently, the hash of the previous block will not match, invalidating the transaction.

In this chapter, we will look at how merkle trees are used to verify the integrity of block transactions. After this, we will implement code for Helium merkle trees.

Tree Data Structures

In Computer Science, a tree is a collection of nodes where the nodes are related to each other through parent, child, and sibling relationships. This is best explained by means of a diagram (Figure 10-1).

Figure 10-1

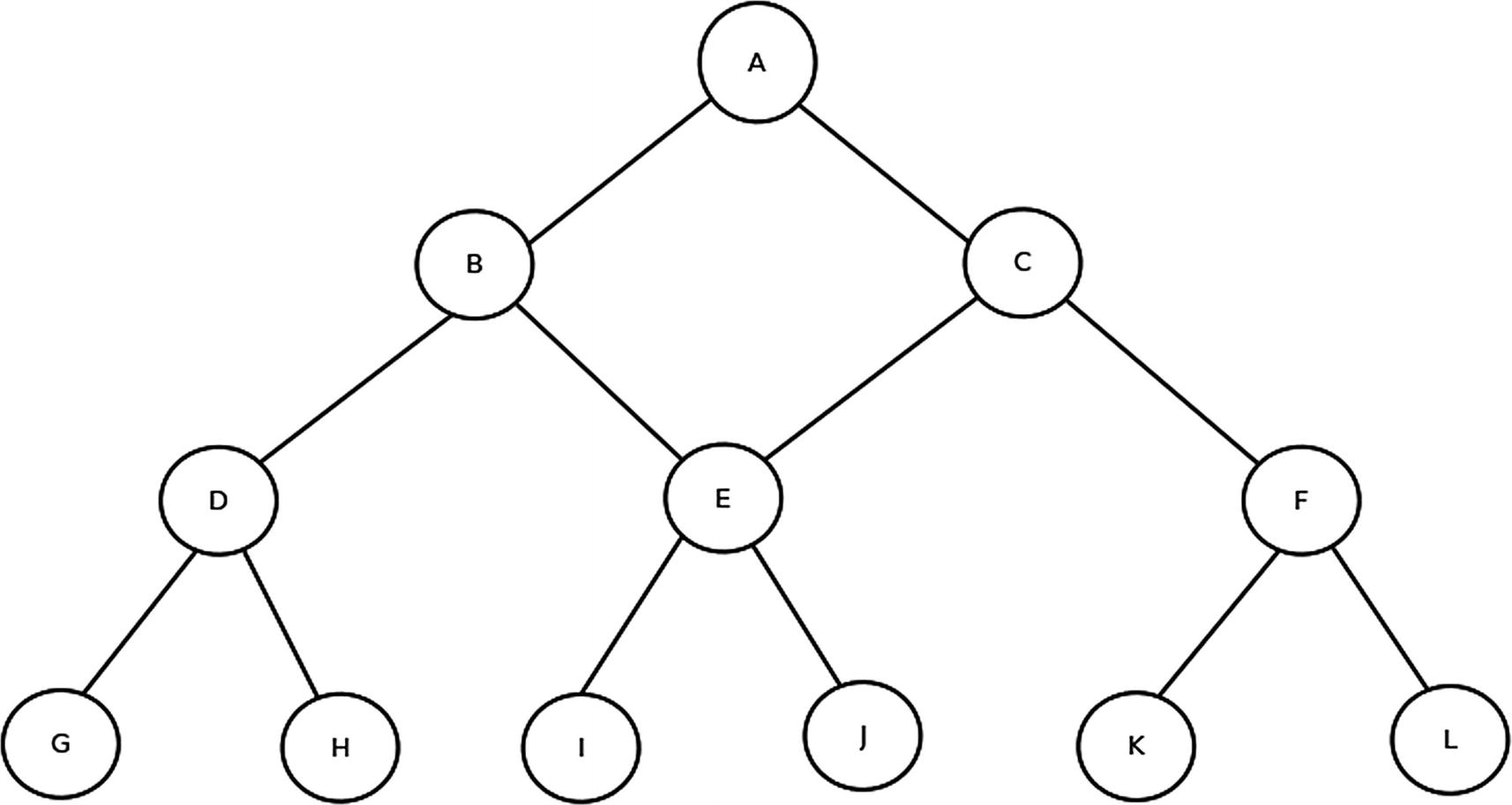
A Tree Data Structure

In this diagram, each node is represented by a circle. There are 12 nodes, labeled from A to L. These nodes are arranged in four layers. Each node, except for node A, is connected to a node above it with a line. The node above it is called a parent node. For example, D is a parent node of H, and C is a parent of E as well as F. Node A does not have a parent; it is called the root node. Aside from the nodes G to L, which are at the bottom of this tree structure, each node is connected to two nodes below it. These two nodes are called the children (or left and right children) of the node above (which is a parent node). For example, node E has two children, the I and J nodes. E is the parent of these nodes. The children nodes of a parent node are called siblings of each other. The nodes at the bottom of the tree do not have any children and are called leaf nodes.

This diagram is an example of a binary tree; all of the nodes except for the leaf nodes have two children. Furthermore, this is a balanced tree since all of the leaf nodes are at the same level. It is not necessary that each parent node have two children or that the tree be balanced. We can construct trees where nodes have a varying number of children and the tree is not balanced. However, balanced binary trees have very nice properties; in particular, we can do very fast insertions and deletions of nodes in the tree. Additionally, searching for a node in these trees is very fast.

Each node in a tree will typically contain pointers to its children, its parent node as well as data specific to the domain in which the tree is being used. The pointers in these nodes permit bidirectional movement through the tree.

Merkle Trees

In typical cryptocurrency implementations, the data portion of a block contains a collection of transactions. For example, a Bitcoin block may contain 2000–4000 transactions. In Helium, the transactions in a block are represented as a list. Each list element is a transaction, and each transaction has a dictionary structure. We will see shortly that we can represent this transaction list as a tree structure.

A merkle tree is a balanced binary tree where the nodes are related through cryptographic hashes. The root node of the merkle tree uniquely identifies the tree.

Suppose that we have a list of eight transactions in a block. We will construct the merkle tree of this list as follows.

For each of these transactions, compute the SHA256 cryptographic hash of the transaction as a hexadecimal string. These values will become the leaf nodes of our merkle tree (Figure 10-2).

Figure 10-2

Leaf Nodes of the Merkle Tree

TnhH is the SHA256 hash of the nth transaction. Since a merkle tree is a balanced binary tree, it must contain an even number of leaf nodes. Therefore, if we have an odd number of transactions in the block, we will simply add the last transaction twice to the transaction list.

We can now derive the second layer of the merkle tree. Starting with the leftmost leaf node, we consider its sibling on the right side. We concatenate the two hashes, T1H and T2H, and compute the SHA256 hash of this concatenated string:

    T12H = SHA256(T1H + T2H)

Then we concatenate the next pair of leaf node hashes and compute the SHA256 hash:

T34H = SHA256(T3H + T4H)

We proceed in this manner until all of the leaf nodes have been processed. This will give us a list of cryptographic hashes whose length is one half of the number of leaf nodes. The nodes in the second layer of the merkle tree are constructed from this new list (Figure 10-3).

Figure 10-3

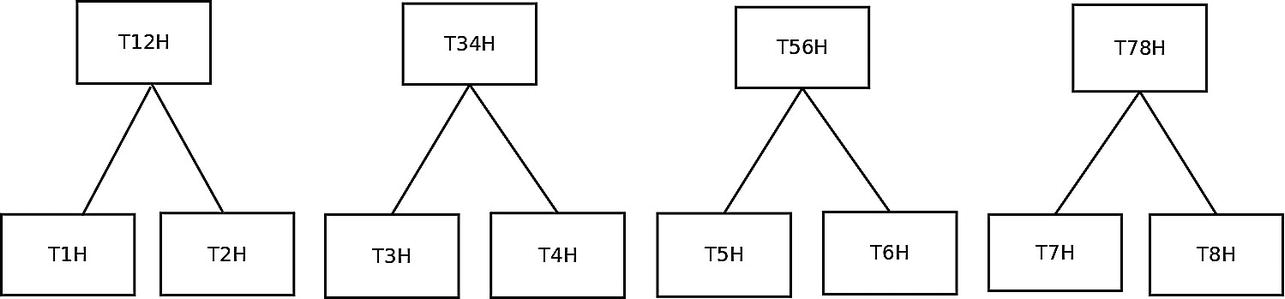
First Two Layers of the Merkle Tree

To derive the third layer of the merkle tree, we compute the hashes:

T1234H = SHA256(T12H + T34H)

T5678H = SHA256(T56H + T78H)

We now have the third layer of the merkle tree (Figure 10-4).

Figure 10-4

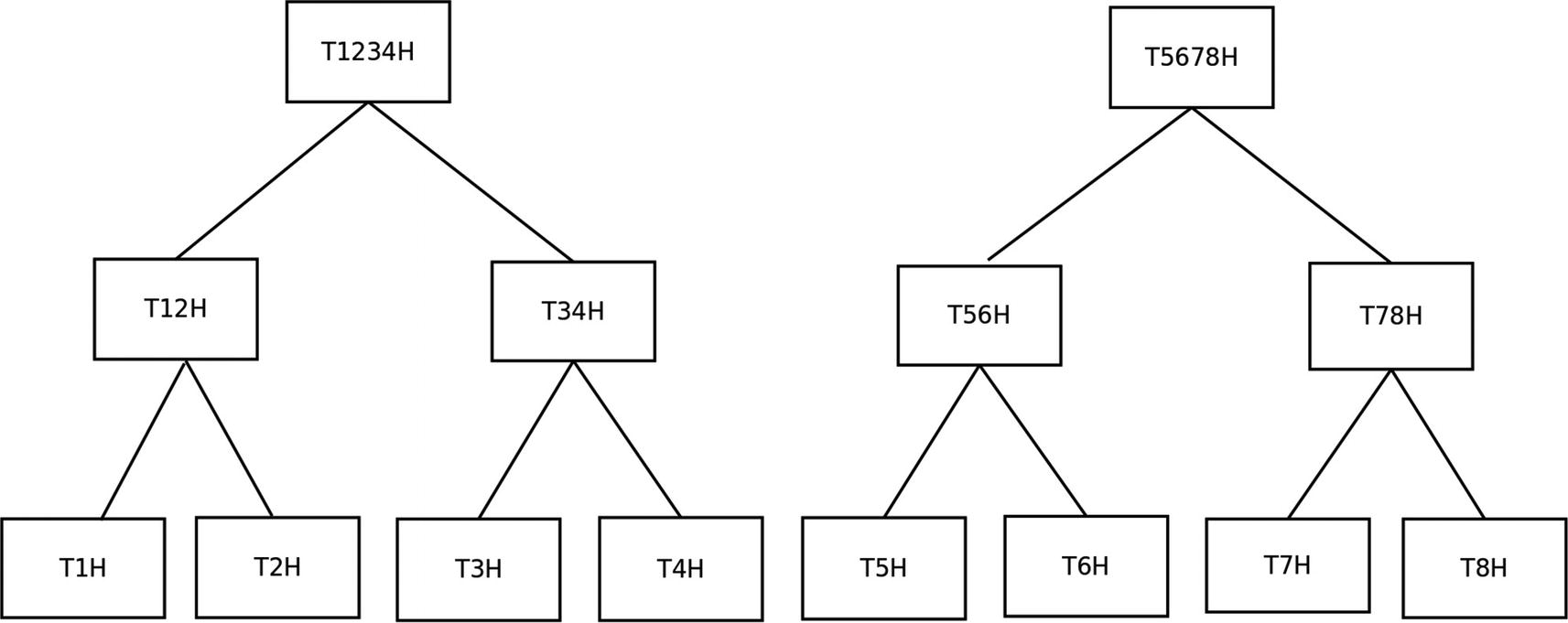
First Three Layers of the Merkle Tree

Finally, we concatenate the SHA256 hashes in the two nodes that are at the third level of the merkle tree:

    T12345678H = SHA256(T1234H + T5678H)

This gives us the final representation of the merkle tree for the eight transactions in the block (Figure 10-5).

Figure 10-5

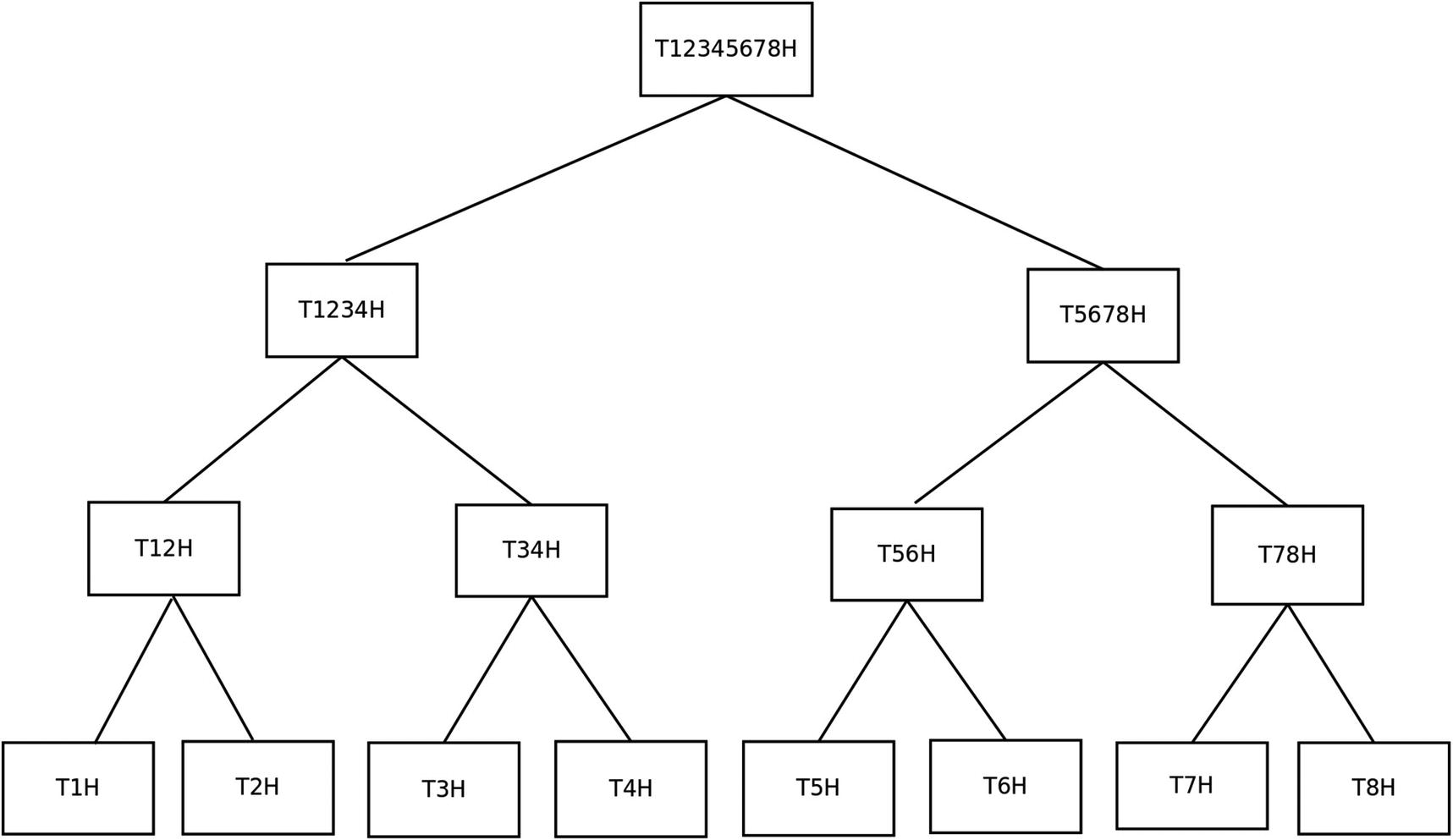
The Merkle Tree for the Eight Block Transactions

The hash value T12345678H is called the merkle root. It is a cryptographic hash of the transactions in the block. If any of the transactions are tampered with or if their order in the transaction list of the block is changed, the merkle root will be inconsistent with its previous value. Since the merkle root is in the block header, the block header will become inconsistent.

You may ask why we need to construct a merkle tree. The short answer is that a balanced binary tree such as a merkle tree is a remarkably efficient search structure. Consider a hypothetical list of one million block transactions. This list can be represented as a merkle tree with a depth of 20 layers. Furthermore, we can search for a particular transaction in this list in O(log n) time where n is the size of the number of transactions.

Another feature of a merkle tree is that the path to any leaf node (transaction) through the merkle tree is unique. Consider the transaction whose SHA256 hash is T6H; the path to this transaction can be represented as

T12345678 + T5678 + T56 + T6

In Figure 10-6, this path is indicated with emphasized lines.

Figure 10-6

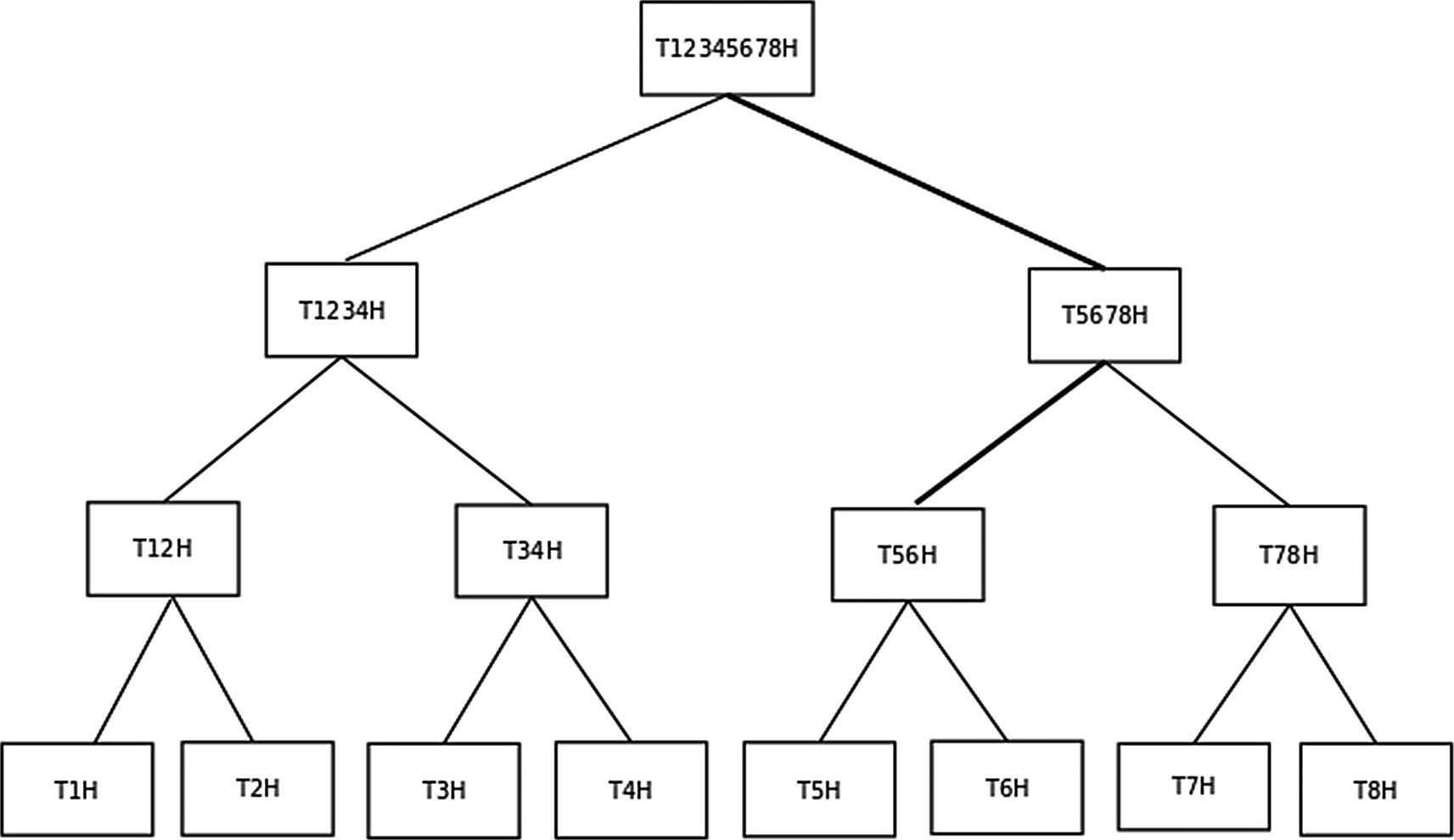
The Path to a Block Transaction

Deriving the Merkle Root in Helium

In Chapter 8, we wrote some of the Python code for the Helium blockchain. The function merkle_root in this module was stubbed out and returned a mocked value. We will now rectify this deficiency and code the function to compute and return the merkle root of a list of transactions in a block.

Remove the stubbed function merkle_root in your hblockchain.py file and add the following code to the bottom of your hblockchain module. The main function merkle_root converts dictionary values into JSON-encoded strings, so ensure that you have imported the standard Python module json into hblockchain:¹

def merkle_root(buffer: "List", start: "bool" = False) -> "bool or string":

    """

    merkle_tree: computes the merkle root for a list of transactions.

    Receives a list of transactions and a boolean flag to indicate whether

    the function has been called for the first time or whether it is a

    recursive call from within the function.

    Returns the root of the merkle tree or False if there is an error.

    """

    try:

        # if start is False then we verify have a list of SHA-256 hashes

        if start == False:

            for value in buffer:

                if rcrypt.validate_SHA256_hash(value) == False:

                    raise(ValueError("tx list SHA-256 validation failure"))

                buflen = len(buffer)

                if buflen != 1 and len(buffer)%2 != 0:

                    buffer.append(buffer[-1])

        # make the merkle leaf nodes if we are entering the function

        # for the first time

        if start == True:

            tmp = buffer[:]

            tmp = make_leaf_nodes(tmp)

            if tmp == False: return False

            buffer = tmp[:]

        # if buffer has one element, we have the merkle root

        if (len(buffer) == 1):

            return buffer[0]

        # construct the list of parent nodes from the child nodes

        index = 0

        parents = []

        while index < len(buffer):

            tmp = rcrypt.make_SHA256_hash(buffer[index] + buffer[index+1])

            parents.append(tmp)

            index += 2

        # recursively call merkle tree

        ret = merkle_root(parents, False)

    except Exception as error:

        logging.error("exception: %s: %s", "merkle_root",error)

        return False

    return ret

def make_leaf_nodes(tx_list: "list") -> "List or False":

    """

    make_leaf_nodes: makes the leaf nodes of a merkle tree.

    Receives a list of transactions. If the number of transactions is an

    odd number, appends the last transaction to the list again so that we can

    make a balanced binary tree.

    Computes the hexadecimal string encoded SHA-256 message digest of each

    transaction and appends it to a leaf node list that is initially empty.

    Returns the leaf node list or False if there is an error

    """

    try:

        # cannot have an empty transaction list

        if (len(tx_list) == 0): raise(ValueError("tx list zero length"))

        # verify we have a list type

        if type(tx_list) is not list: raise(ValueError("tx is not a list type"))

        # verify the type of each transaction is a dict

        for tx in tx_list:

            if type(tx) is not dict: raise(ValueError("tx is not a dict type"))

        # must have an even number of transactions

        if len(tx_list) % 2 == 1 or len(tx_list) == 1:

            tx_list.append(tx_list[- 1] )

        # copy the transaction list

        trx_list = list(tx_list)

        # convert each transaction into a JSON string

        tx = []

        for transaction in trx_list:

            tx.append(json.dumps(transaction))

        # make the leaf nodes

        sha256_list = []

        for transaction in tx:

            sha256_list.append(rcrypt.make_SHA256_hash(transaction))

    except Exception as err:

        logging.debug('make_leaf_nodes: exception: ' + str(err))

        return False

    return sha256_list

There are two functions: merkle_root and make_leaf_nodes. merkle_root receives a list of block transactions. merkle_root is called by the validate_block and blockheader_hash functions.

merkle_root is a recursive function; it receives a boolean flag as its second parameter. This flag is True if merkle_root is called from the aforementioned functions and False if this function has been called by itself. The very first thing that merkle_root does is to call the function make_leaf_nodes, whose task is to construct the leaf nodes of the merkle tree.

make_leaf_nodes performs some validation on the transaction list that it receives. If this list is empty, it returns False. An empty transaction list will have no leaf nodes. It then does some type checking to verify that it has received a list and not some other data structure. It also verifies that each list element is a dictionary type. If things are amiss, it returns a False value. Otherwise, make_leaf_nodes constructs the leaf nodes of the merkle tree for this transaction list and returns these values.

merkle_root then processes the leaf nodes to construct the merkle tree by calling itself recursively with the flag argument set to False.

As I previously indicated, Appendix 10 of this book contains the final source code for all of the Helium modules.

Pytests for the Merkle Code

We will now write some pytest unit tests to validate the merkle code. Add the following pytest code to the bottom of your test_blockchain module.

Once the unit test code has been added, run the tests from the unit_tests directory:

$(virtual) pytest test_blockchain.py -k -s

You should observe a total of 30 tests passing:

def test_empty_merkle_root(monkeypatch):

    """

    test that the merkle root of a block cannot be empty

    """

    hblockchain.blockchain.clear()

    monkeypatch.setattr(hblockchain, "merkle_root", lambda x, y: "")

    assert hblockchain.add_block(block_1) == False

    hblockchain.blockchain.clear()

def test_invalid_merkle_root(monkeypatch):

    """

    test an invalid merkle root

    """

    monkeypatch.setattr(hblockchain, "merkle_root", lambda x, y: rcrypt.make_SHA256_hash('msg1'))

    monkeypatch.setitem(block_1, "merkle_root",  \

      "A88a1fd32a1f83af966b31ca781d71c40f756a3dc2a7ac44ce89734d2186f63z")

    assert hblockchain.add_block(block_1) == False

"""

test the merkle root

These merkle tests do not test the validity of transactions

"""

def test_merkle_root_empty_tx(monkeypatch):

    """

    test the merkle root for an empty transaction list

    """

    monkeypatch.setattr(hblockchain, "merkle_root", \

      lambda x, y: rcrypt.make_SHA256_hash('msg0'))

    monkeypatch.setitem(block_0, "tx", [])

    monkeypatch.setattr(hblockchain, "merkle_root", \

      lambda x, y: rcrypt.make_SHA256_hash('msg1'))

    monkeypatch.setitem(block_1, "tx", [])

    assert hblockchain.add_block(block_1) == False

def test_merkle_root_tx_bad_type():

    """

    test the merkle root for a bad transaction list type

    """

    assert bool(hblockchain.merkle_root ("123", True)) == False

def test_merkle_bad_flag():

    """

    test the merkle root for a bad flag parameter

    """

    assert bool(hblockchain.merkle_root ([{"a":1}], False)) == False

def test_merkle_root_transactions_dict_type():

    """

    test the merkle root for a transaction list is a dict type

    """

    assert bool(hblockchain.merkle_root ({'a': 1}, True)) == False

def test_merkle_root_random_transaction():

    """

    test merkle root for synthetic random transactions

    does not test hash of previous block

    """

    hblockchain.blockchain.clear()

    block_0["merkle_root"] = hblockchain.merkle_root(block_0["tx"], True)

    assert hblockchain.add_block(block_0) == True

    block_1["merkle_root"] = hblockchain.merkle_root(block_1["tx"], True)

    block_1["prevblockhash"] = hblockchain.blockheader_hash(block_0)

    assert hblockchain.add_block(block_1) == True

    block_2["merkle_root"] = hblockchain.merkle_root(block_2["tx"], True)

    block_2["prevblockhash"] = hblockchain.blockheader_hash(block_1)

    assert hblockchain.add_block(block_2) == True

Conclusion

Merkle trees are important in blockchain applications for two principal reasons. Firstly, they permit us to efficiently test whether a list of transactions has been tampered with. Secondly, we can use these trees to verify whether a particular transaction is in a transaction list. In this chapter, we have examined merkle trees and written code to make a merkle tree from a list of transactions in a block.

In the next chapter, we will write transaction code for Helium and unit test this code.

Footnotes

1

JSON encoding and decoding is explained at https://docs.python.org/3/library/json.html, last accessed on February 7, 2020