K. S. GarewalPractical Blockchains and Cryptocurrencieshttps://doi.org/10.1007/978-1-4842-5893-4_5

5. The Alchemy of Public Key Cryptosystems

Karan Singh Garewal¹

(1)

Toronto, ON, Canada

This chapter is concerned with what can be termed modern cryptography or asymmetric cryptography. In Chapter 3, we studied symmetric encryption and surmised that it has a significant scalability problem when the encryption key has to be distributed to a large number of recipients. For example, consider the scenario where an encryption key has to be distributed to thousands of recipients. Each transmission of the key to a recipient carries with it, a certain probability that the key will be intercepted by a malevolent actor. The aim of public key cryptosystems, inter alia, is to solve this scalability problem and also render moot the issue of the interception of the secret key by adversaries. The piece de resistance of the theory of public key cryptosystems are digital signature algorithms; these solve three problems simultaneously: (i) assuring the integrity of messages, (ii) assuring the authenticity of messages, and (iii) solving the scalability problem.

Public key cryptosystems find usage in a myriad of modern applications. For example, they are used in secure HTTP communications, virtual private networks, credit cards, ecommerce systems, smart cards, electronic identity cards, and international payment systems such as SWIFT and now in cryptocurrencies and blockchain applications.

In this chapter, I am going to start by summarizing the problem of distributing symmetric encryption keys and then provide a brief description of the canonical digital signature algorithm. After this, I will provide you with some of the mathematical theory underlying public key cryptosystems and finally proceed to discuss digital signature algorithms in greater depth. I will also provide code examples in Python as we proceed.

The Key Distribution Problem Revisited

Once again, suppose that you and I are at the opposite ends of the Milky Way and that I want to send you a secret message. Firstly, you must possess the symmetric encryption key so that you can decrypt the message. Thus, if you do not have this key, I must transmit it to you. After I provide you with the key, I can then send encrypted messages to you and you will be able to decrypt them using the secret key. In order to detect whether the message has been altered while in transit, I can also transmit the SHA-256 hash of either the plaintext or encrypted message to you. This cryptographic hash can be appended to the message.

In the previous scenario, there are two outstanding issues which have to be addressed. Firstly, you do not know whether the message has actually been sent by me or by some hostile actor who is impersonating me. The message could have been crafted by anyone who has the encryption key. This is the authenticity problem. How do we prove that a message has been sent by the person who purports to be its author? The second issue is that the encryption key could have been intercepted by a hostile entity while in transit. There is no deterministic way to prove that the secret key has not been intercepted while in transit. This problem is compounded when the key has to be distributed to a large number of recipients. Consider, for example, an intelligence-gathering network where each node in the network must be supplied with the encryption key.

Heuristics of Digital Signature Algorithms

In public key cryptography, an asymmetric key generation algorithm is used to generate a public key and a private key pair. Each of these keys is a very long string. The person generating this key pair keeps the private key securely with him- or herself and distributes the public key to his intended recipients. For example, the public key can be distributed to the world at large by posting it on the Internet. The essential aspect of the distribution of the public key is that we do not care that a hostile entity has possession of this key. Since the entity that generates the key pair must keep the private key securely with himself, it is important that the asymmetric key generation algorithm makes it computationally infeasible to recover the private key from the public key.

A person can now encrypt a message with the public key and transmit it to the holder of the private key or simply post the encrypted message on the Internet. The asymmetric key generation algorithm guarantees that this message can only be decrypted with the private key, that is, it is computationally infeasible to decrypt the message without the private key. By computational infeasibility, we mean that it would take an enormous amount of time (perhaps eons) to decrypt the message in the absence of the private key.

Similarly, a message encrypted with the private key can only be decrypted by the public key corresponding to the private key. It is computationally infeasible for an adversary to recover the original message from the ciphertext without the public key. The public and private keys are inverses of each other in the sense that encryption operations performed by either key can be reversed by the other key. This is the essence of public key cryptosystems. Figure 5-1 shows this process.

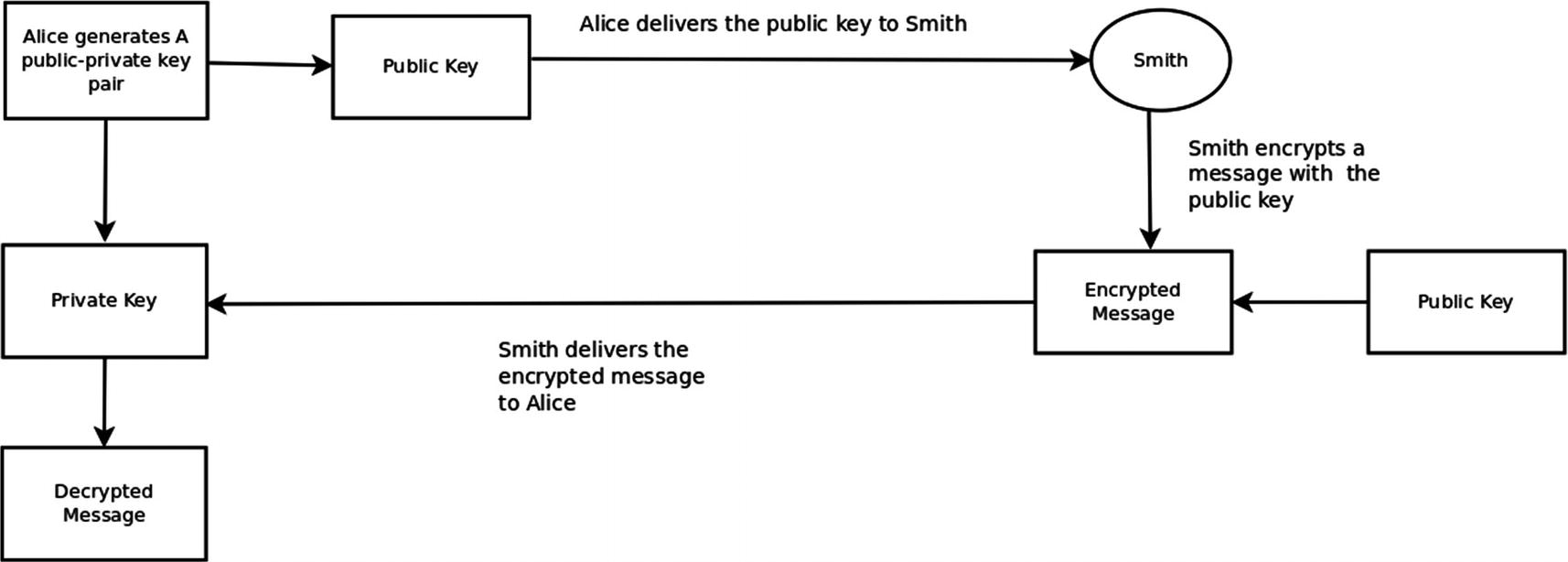
../images/492478_1_En_5_Chapter/492478_1_En_5_Fig1_HTML.jpg — Figure 5-1
Public Key Cryptosystem

In the preceding process, Alice generates a public-private key pair and delivers the public key to Smith while keeping the private key securely with herself. Smith then encrypts a message with this public key and delivers the ciphertext to Alice. Alice then decrypts the ciphertext with her private key.

Alice knows that the message has been encrypted by a person who has the public key, but typically Alice will not know the identity of the person who actually encrypted this message (unless Alice knows with certainty that only Smith has the public key). The determination of this identity issue requires a public key infrastructure (PKI). We will discuss public key infrastructures shortly.

The other scenario is when Alice encrypts a message with her private key. Such a message can be decrypted by any person who holds the corresponding public key. The essential feature here is that the recipient of the message can conclude that the message was generated by the entity holding the private key. Furthermore, Alice cannot repudiate the assertion that the message was generated with the private key held by her. Note that in the absence of exogenous information, the recipient cannot associate the private key with Alice. One way of establishing such associations is through the use of certificate authorities (PKI).

Alice and Smith can engage in secure bidirectional communications if each party sends messages using the other party’s public key.

Digital signature algorithms address two issues: firstly that a message has not been tampered with and secondly that the signature has been generated by a certain private key and hence by the holder of this key. The second aspect of the algorithm solves the authentication problem.

These algorithms consist of two stages: a signature generation stage and a signature verification stage. Figure 5-2 shows the steps involved in the signature generation stage.

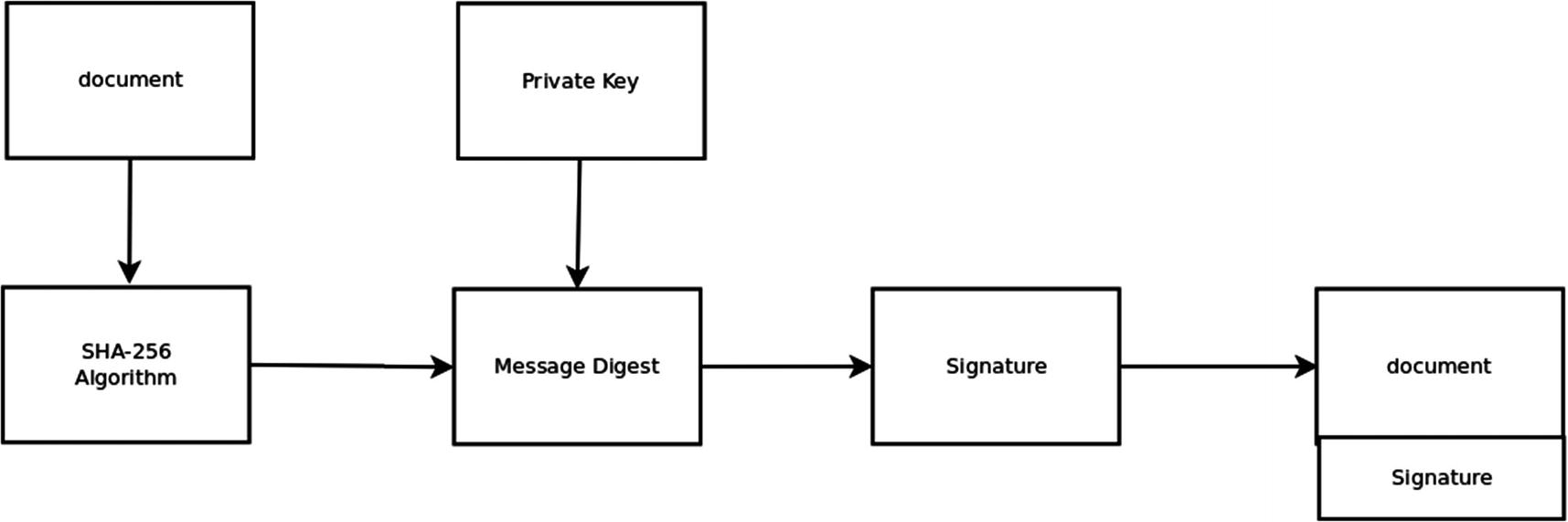
../images/492478_1_En_5_Chapter/492478_1_En_5_Fig2_HTML.jpg — Figure 5-2
Producing the Digital Signature of a Document

Alice has generated a public private key pair and has a document that she wants to digitally sign.¹ In the first step, Alice generates a cryptographic hash of the document, say, the SHA-256 message digest of the document. Alice then encrypts the message digest with her private key. The result of this encryption is the digital signature of the document. In the second step, Alice concatenates the document and the digital signature and transmits this concatenated document to the recipient.

As we have noted previously, high-quality cryptographic algorithms such as SHA-256 have an avalanche effect. If a document is changed very slightly, even by a single bit, this will produce a message digest which changes dramatically. This same avalanche effect occurs when the private key is applied to the message digest. Lastly, note that the document itself need not be encrypted. In many important applications, we do not care that the document is transmitted in plaintext since our only concern is with detecting alteration of the document and with the authentication of the document. Of course, Alice can also choose to encrypt the document with her private key and then encrypt the SHA-256 message digest of the encrypted document with her private key.

The second stage of digital signature algorithms is the verification of the document by a recipient of the document. Figure 5-3 shows this process.

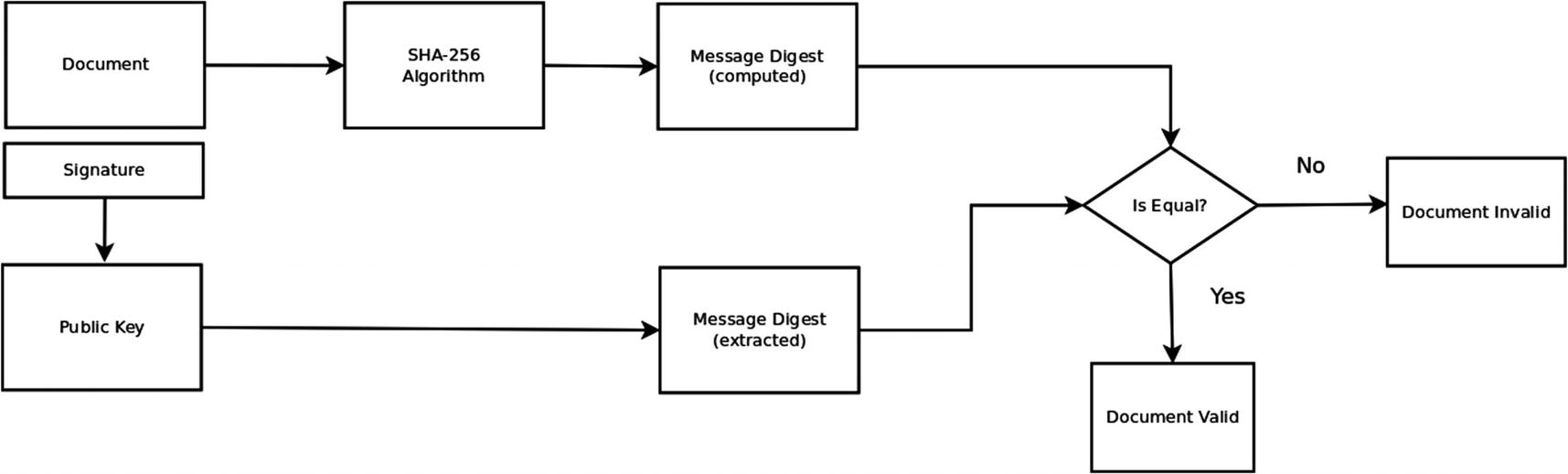
../images/492478_1_En_5_Chapter/492478_1_En_5_Fig3_HTML.jpg — Figure 5-3
Verifying the Digital Signature of a Document

In the verification stage, the recipient of the concatenated document (say Smith) separates the document and the signature. In the first step, Smith computes the SHA-256 message digest of the document that has been received. In the second step, the signature that was concatenated with the document is decrypted by applying Alice’s public key to the signature. This yields the message digest which was computed by the sender of the document. The two message digests are then compared. If the message digests are equal, then Smith can conclude that the document has not been tampered with while in transit and that Alice has signed and delivered this document since her private key matches the public key that Smith has used. If the message digests do not match, then there are three possibilities. Firstly, the document has been altered while in transit; secondly, Alice is not the author of the document; and lastly Smith does not possess the public key corresponding to Alice’s private key.

Public Key Infrastructure

As you will recall, when Smith receives a message (or document) encrypted with a private key, all that he can infer about the identity of the sender is that this entity is in possession of the private key that encrypted the message. Smith must possess exogenous information in order to associate the identity of Alice with the private key. Similarly, when Alice receives a message that has been encrypted with her public key, then in the absence of exogenous information, she can only conclude that the message has been encrypted by someone holding her public key.

One way to associate an identity with a public key (and implicitly its private key) is through a certificate authority (CA). The following is the manner in which certificate authorities work. Firstly, the certificate authority obtains information on the identity of the applicant who claims to own a private-public key pair. The applicant provides the CA with his public key. The CA then asks the applicant to digitally sign a document provided by the CA. After the applicant has signed the document, the CA proceeds to verify the signature of the document. If the verification succeeds, it is proof that the applicant is in possession of the private key pertaining to the public key that he has supplied to the CA. The CA then issues an X.509 certificate to the applicant. This certificate is signed by the CA with its private key to prove the identity of the certificate issuer and to assure that it has not been altered. The issued certificate typically contains information identifying the applicant, such as the name, address, and other distinguishing particulars, the public key generated by the applicant, the expiry date of the certificate, and so forth.

Alice can provide proof of the authorship of a document in the following manner. Firstly, Alice will encrypt her certificate with her private key and concatenate it with the document she wants to deliver. Alice will digitally sign this concatenated document and attach the signature to the concatenated document. This will enable the recipient to securely verify the identity of the person who has signed the document by decrypting the certificate.

In a similar manner, when Smith encrypts a document with Alice’s public key, he can also encrypt his certificate with his private key and concatenate the encrypted certificate with the document. Alice will now know the identity of the person who has sent her the document encrypted with her public key by decrypting the certificate with Smith’s public key.

The RSA Algorithm

Several public-private key generation algorithms exist in the public domain. The two leading algorithms are RSA and the Elliptic Curve Digital Signature Algorithm (ECDSA) . The RSA algorithm is the most widely used public key algorithm.² These algorithms rely upon computationally intractable problems in Mathematical Number Theory. For example, RSA relies on the fact that it is computationally infeasible to factor an extremely large number into a product of primes. ECDSA relies upon the difficulty of finding the discrete logarithms of extremely large numbers. The bitcoin code uses public-private key pairs that are generated using the Elliptic Curve Digital Signature Algorithm.

In this optional section, we are going to derive the RSA algorithm. Before we do this, we need a few pieces from Number Theory:

Definition (prime number): A positive integer n greater than 1 is called a prime number if it is only divisible by +1, -1, -n and n.

Theorem (the fundamental theorem of arithmetic): Any integer m > 1 can be factored into a product of prime numbers

m = p₁^t1p₂^t2p₃^t3 … p_n^tn

where p₁ < p₂ < … < p_n are prime numbers and t1, t2, … tn are natural numbers greater than 0.

Definition (relatively prime numbers): Two positive integers j > 1 and k > 1 are said to be relatively prime if their only common factor is 1.

For example, 6 and 9 are not relatively prime since 3 is a common divisor. 8 and 15 are relatively prime.

Definition (Euler’s totient function, Q(n)): For any integer n > 1, Q(n) is the number of positive integers less than n that are relatively prime to n.

For example, Q(15) = 7 since the set of relatively prime numbers is { 2,4,7,8,11,13,14 }.

Theorem (Euler’s theorem): For any integers a,n > 1 where a and n are relatively prime, a^Q(n) % n = 1.³

For example, let a = 15 and n = 8, Q(n) = 4, and then

15⁴ % 8 = 50625 % 8 = 1

It should be clear that for a natural number m > 1, the prime factorization p₁^t1p₂^t2p₃^t3 … p_n^tn is unique. The RSA algorithm relies upon the fact that it is computationally infeasible to obtain the prime factorization of very large numbers.

We can now derive an RSA public-private key pair as follows:

Step 1: Choose two large random prime numbers p and q where p does not equal to q.

Step 2: Calculate the product: n = pq.

Step 3: Because p and q are prime numbers, Euler’s totient function value for n is Q(n) = (p-1)(q-1).

Step 4: Choose an integer 1 < e < Q(n) such that e and Q(n) are relatively prime.

Step 5: Get a positive integer d so that de % Q(n) = 1.

The public key is the tuple (n, e). The private key is the tuple (p, q, d). The public key tuple can be distributed freely; the private key tuple is kept secret.

Let us now look at the application of the RSA algorithm. Consider a document or message D. D can be viewed as a very long sequence of bits or equivalently as a massively large positive integer. Henceforth, we will consider D as such an integer. We make sure that our prime numbers p and q have been selected so that D < pq.

Smith, who has received the public key tuple (n, e), creates the encrypted message C as follows:

C = D^e % n

C is a positive integer or equivalently is a very long sequence of bits.

Alice can now use her private key tuple (p, q, d) to decrypt the ciphertext:

D = C^d % n

As a concrete example, let p = 7 and q = 5.

n = pq = 35

Then Q(35) = 24 and we select e = 17.

e and Q(n) are relatively prime.

We select d such that de % Q(n) = 17d % 24 = 1

d = 17

Now consider a document T = 12

Then the ciphertext is 12¹⁷ % 35 = 17

We decrypt the ciphertext with 17¹⁷ % 35 = 12

RSA public-private key encryption is the most widely used private-public key encryption system. It is just as secure as keys generated using elliptic curve cryptography (ECDSA). Following Bitcoin, we will use ECDSA key pairs. The logic of such keys is conceptually similar to RSA keys, and I will omit discussing their generation since a rigorous discussion of the underlying Mathematics will take us into a long digression. Our Blockchain code will contain the necessary library functions to generate ECDSA public-private key pairs.

Python Code Example

In the following Python example, we will use the pycryptodome package to lead Alice and Smith through a sequence of encryption, decryption, signature generation, and signature verification steps using RSA.⁴ You should walk through this code carefully to see the mechanics of using public and private key pairs to encrypt and decrypt messages.

If you have not already done so, install this package:⁵

pip3 install pycryptodome

#========================================

# RSA Public-key cryptography example

#========================================

from Crypto.PublicKey import RSA

from Crypto.Cipher import PKCS1_OAEP

from Crypto.Hash import SHA256

from Crypto import Random

from hashlib import sha256

import binascii

#=====================================

# generate a RSA key-pair

#=====================================

def RSAKeyPair(keylength):

keyPair = RSA.generate(keylength)

return keyPair

# Alice generates a RSA key-pair

AliceKeyPair = RSAKeyPair(1024)

# Alice's public-key

pubKey = AliceKeyPair.publickey()

print(f"public-key: (n={hex(pubKey.n)}, e={hex(pubKey.e)})")

# Alice's public-key in PEM format

# PEM format Base64 encodes the key

pubKeyPEM = AliceKeyPair.publickey().exportKey()

print("PubKey PEM Format: " +pubKeyPEM.decode('ascii'))

# Alice's private key

print(f"Private key: (n={hex(pubKey.n)}, d={hex(AliceKeyPair.d)})")

# Alice's private key in PEM format

privKeyPEM = AliceKeyPair.exportKey()

print("PRIVATE KEY PEM FORMAT; " + privKeyPEM.decode('ascii'))

#======================================================

# Smith encrypts a message using Alice's public-key

# message must be a binary string

#======================================================

message = b"The quick brown fox jumped over the farmer's hedge"

cipher = PKCS1_OAEP.new(pubKey)

cipherText = cipher.encrypt(message)

print("CipherText: ", binascii.hexlify(cipherText))

#=======================================================

# Alice decrypts Smith's message using her private key

#=======================================================

decipher = PKCS1_OAEP.new(AliceKeyPair)

plainText = decipher.decrypt(cipherText)

print('Decrypted Text: ', plainText)

#==========================================================

# Alice signs a message by first generating the SHA-256

# digest of the message and then encrypting it with her

# private key.

# the string message is converted to a binary string

#==========================================================

message = b'let sleeping dogs lie, said the farmer'

hash = int.from_bytes(sha256(message).digest(), byteorder="big")

signature = pow(hash, AliceKeyPair.d, AliceKeyPair.n)

print("Alice's Signature:", hex(signature))

#============================================================

# Smith Verifies the signature by comparing the SHA-256 hash

# generated from the received message with the hash obtained

# by decrypting the signature received from Alice

#=============================================================

hashFromMessage = int.from_bytes(sha256(message).digest(), byteorder="big")

decryptedHash = pow(signature, AliceKeyPair.e, AliceKeyPair.n)

if (hashFromMessage == decryptedHash):

print("Signature is valid")

else:

print("signature is invalid")

Generating Globally Unique IDs

In a blockchain application, we typically need universally unique values that identify blocks and transactions. One way to generate these global IDs is to generate a public-private key pair and then get the SHA-256 hash of the private or public key. The resultant 256-bit message digest is globally unique.⁶ This means that it is computationally infeasible to generate some other public-private key pair that will generate the same message digest. Similarly, we can apply the RIPEMD-160 cryptographic hash function to a public or private key. The resultant 160-bit message hash is also a globally unique id.

Conclusion

Public key cryptography or asymmetric key encryption is a very important foundational tool of blockchain and cryptocurrency applications. In this chapter, we have delved into public key cryptography and, in particular, public-private key pairs and digital signature algorithms. We have also looked at the derivation of the RSA algorithm, which is the most popular algorithm for generating public-private key pairs. In addition, we have described a public key infrastructure which can be used to associate identities with these key pairs.

This constitutes the end of our dive into cryptography, and in the next chapter, we will proceed to the main corpus of this book, blockchain and cryptocurrency applications.