5 The computational universe
It is no secret that we are in the midst of an information-processing revolution based on electronic computers and optical
communication systems. This revolution has transformed work, education, and thought, and has affected the life of every person
on Earth.
5.1 The information-processing revolutions
The effect of the digital revolution on humanity as a whole, however, pales when compared with the effect of the previous
information-processing revolution: the invention of moveable type. The invention of the printing press was an information-processing
revolution of the first magnitude. Moveable type allowed the information in each book, once accessible only to the few people
who possessed the book’s hand-copied text, to be accessible to thousands or millions of people. The resulting widespread literacy
and dissemination of information completely transformed society. Access to the written word empowered individuals not only
in their intellectual lives, but in their economic, legal, and religious lives as well.
Similarly, the effect of the printed word is small when compared with the effect of the written word. Writing – the discovery
that spoken sounds could be put into correspondence with marks on clay, stone, or paper – was a huge information-processing
revolution. The existence of complicated, hierarchical societies with extended division of labor depends crucially on writing.
Tax records figure heavily in the earliest cuneiform tablets.
Just as printing is based on writing, writing stems from one of the greatest information-processing revolutions in the history
of our planet: the development of the spoken word. Human language is a remarkable form of information processing, capable
of expressing, well, anything that can be put into words. Human language includes within it the capacity to perform sophisticated
analysis, such as mathematics and logic, as well as the personal calculations (“if she does this, I’ll do that”) that underlie
the complexity of human society.
Although other animals have utterance, it is not clear that any of them possess the same capacity for universal language that
humans do. Ironically, the entities that possess the closest approximation to human language are our own creations: digital
computers, whose computer languages possess a form of universality bequeathed to them by human language. It is the social
organization stemming from human language (together with written language, the printed word, computers, etc.) that have made
human beings so successful as a species, to the extent that the majority of the planet’s resources are now organized by humans
for humans. If other species could speak, they would probably say, “Who ordered that?”.
Before turning to even earlier information-processing revolutions, it is worth saying a few words about how human language
came about. Who “discovered” human language? The fossil record, combined with recently revealed genetic evidence, suggests
that human language may have arisen between 50 and 100 000 years ago, in Africa. Fossil skulls suggest that human brains underwent
significant change over that time period, with the size of the cortex expanding tenfold. The result was our species, Homo sapiens: “man with knowledge” (literally, “man with taste”). Genetic evidence suggests that all women living today share mitochondrial
DNA (passed from mother to daughter) with a single woman who lived in Africa around 70 000 years ago. Similarly, all men share
a Y chromosome with one man who lived at roughly the same time.
What evolutionary advantage did this Adam and Eve possess over other hominids that allowed them to populate the world with
their offspring? It is plausible that they possessed a single mutation or chance combination of DNA that allowed their offspring
to think and reason in a new and more powerful way (Chomsky et al., 2002). Noam Chomsky has suggested that this way of reasoning should be identified with recursion, the ability to construct hierarchies
of hierarchies, which lies at the root both of human language and of mathematical analysis. Once the ability to reason had
appeared in the species, the theory goes, individuals who possessed this ability were better adapted to their immediate surroundings,
and indeed, to all other surroundings on the planet. We are the offspring of those individuals.
Once you can reason, there is great pressure to develop a form of utterance that embodies that reason. Groups of Homo sapiens who could elaborate their way of speaking to reflect their reasoning would have had substantial evolutionary advantage over
other groups who were incapable of complex communication and who were therefore unable to turn their thoughts into concerted
action.
I present this plausible theory on the origin of language and of our species to show that information-processing revolutions
need not be initiated by human beings. The “discovery” of a new way of processing information can arise organically out of
an older way. Apparently, once the mammalian brain had evolved, then a few mutations gave rise to the ability to reason recursively.
Once the powerful information-processing machinery of the brain was present, language could evolve by accident, coupled with
natural selection.
Now let us return to the history of information-processing revolutions. One of the most revolutionary forms of information
processing is sex. The original sexual revolution (not the one of the 1960s) occurred some billion years ago when organisms learned to share
and exchange DNA. At first, sex might look like a bad idea: when you reproduce sexually, you never pass on your genome intact.
Half of your DNA comes from your mother, and half from your father, all scrambled up in the process called recombination.
By contrast, an asexually reproducing organism passes on its complete genome, modulo a few mutations. So even if you possess a truly fantastic combination of DNA, when you reproduce sexually, your offspring
may not possess that combination. Sex messes with success.
So why is sex a good idea? Exactly because it scrambles up parents’ DNA, sexual reproduction dramatically increases the potential
rate of evolution. Because of the scrambling involved in recombination, sexual reproduction opens up a huge variety of genetic
combinations for your offspring, combinations that are not available to organisms that rely on mutation alone to generate
genetic variation. (In addition, whereas most mutations are harmful, recombination assures that viable genes are recombined
with other viable genes.) To compare the two forms of reproduction, sexual and asexual, consider the following example: by
calculating the number of genetic combinations that can be generated, it is not hard to show that a small town of 1000 people,
reproducing sexually with a generation time of 30 years, produces the same amount of genetic variation as a culture of one
trillion bacteria, reproducing asexually every 30 minutes.
Sex brings us back to the mother of all information-processing revolutions: life itself. However it came about, the mechanism
of storing genetic information in DNA, and reproducing with variation, is a truly remarkable “invention” that gave rise to
the beautiful and rich world around us. What could be more majestic and wonderful? Surely, life is the original information-processing
revolution.
Or is it? Life arose on Earth some time in the last five billion years (for the simple reason that the Earth itself has only
been around for that long). Meanwhile, the universe itself is a little less than fourteen billion years old. Were the intervening
nine billion years completely devoid of information-processing revolutions?
The answer to this question is “No.” Life is not the original information-processing revolution. The very first information-processing
revolution, from which all other revolutions stem, began with the beginning of the universe itself. The big bang at the beginning
of time consisted of huge numbers of elementary particles, colliding at temperatures of billions of degrees. Each of these
particles carried with it bits of information, and every time two particles bounced off each other, those bits were transformed and
processed. The big bang was a bit bang. Starting from its very earliest moments, every piece of the universe was processing
information. The universe computes. It is this ongoing computation of the universe itself that gave rise naturally to subsequent
information-processing revolutions such as life, sex, brains, language, and electronic computers.
5.2 The computational universe
The idea that the universe is a computer might at first seem to be only a metaphor. We build computers. Computers are the
defining machines of our era. Consequently, we declare the universe to be a computer, in the same way that the thinkers of
the Enlightenment declared the universe to be a clockwork one. There are two responses to this assertion that the computational
universe is a metaphor. The first response is that, even taken as a metaphor, the mechanistic paradigm for the universe has
proved to be incredibly successful. From its origins almost half a millennium ago, the mechanistic paradigm has given rise
to physics, chemistry, and biology. All of contemporary science and engineering comes out of the mechanistic paradigm. To
think of the universe not just as a machine, but also as a machine that computes, is a potentially powerful extension of the
mechanistic paradigm.
The second response is that the claim that the universe computes is literally true. In fact, the scientific demonstration
that all atoms and elementary particles register bits of information, and that every time two particles collide those bits
are transformed and processed, was given at the end of the nineteenth century, long before computers occupied people’s minds.
Beginning in the 1850s, the great statistical mechanicians James Clerk Maxwell in Cambridge and Edinburgh, Ludwig Boltzmann
in Vienna, and Josiah Willard Gibbs at Yale, derived the mathematical formulae that characterized the physical quantity known
as entropy (Ehrenfest and Ehrenfest, 2002). Prior to their work, entropy was known as a somewhat mysterious thermodynamic quantity that gummed up the works of steam engines, preventing them from doing as much work as they
otherwise might do. Maxwell, Boltzmann, and Gibbs wanted to find a definition of entropy in terms of the microscopic motions
of atoms. The formulae that they derived showed that entropy was proportional to the number of bits of information registered
by those atoms in their motions. Boltzmann then derived his eponymous equation to describe how those bits were transformed
and flipped when atoms collide. At bottom, the universe is processing information.
The scientific discovery that the universe computes long preceded the formal and practical idea of a digital computer. It
was not until the mid twentieth century, however, with the work of Claude Shannon and others, that the interpretation of entropy
as information became clear (Shannon and Weaver, 1963). More recently, in the 1990s, researchers showed just how atoms and elementary particles compute at the most fundamental
level (Chuang and Nielsen, 2000). In particular, these researchers showed how elementary particles could be programmed to perform conventional digital computations
(and, as will be discussed below, to perform highly unconventional computations as well). That is, not only does the universe
register and process information at its most fundamental level, as was discovered in the nineteenth century, it is literally
a computer: a system that can be programmed to perform arbitrary digital computations.
You may ask, So what? After all, the known laws of physics describe the results of experiments to exquisite accuracy. What
does the fact that the universe computes buy us that we did not already know?
The laws of physics are elegant and accurate, and we should not discard them. Nonetheless, they are limited in what they explain.
In particular, when you look out your window you see plants and animals and people; buildings, cars, and banks. Turning your
telescope to the sky you see planets and stars, galaxies and clusters of galaxies. Everywhere you look, you see immense variation
and complexity. Why? How did the universe get this way? We know from astronomical observation that the initial state of the universe, fourteen billion years ago, was extremely flat, regular,
and simple. Similarly, the laws of physics are simple: the known laws of physics could fit on the back of a T-shirt. Simple
laws, simple initial state. So where did all of this complexity come from? The laws of physics are silent on this subject.
By contrast, the computational theory of the universe has a simple and direct explanation for how and why the universe became
complex. The history of the universe in terms of information-processing revolutions, each arising naturally from the previous
one, already hints at why a computing universe necessarily gives rise to complexity. In fact, we can prove mathematically
that a universe that computes must, with high probability, give rise to a stream of ever-more-complex structures.
5.3 Quantum computation
In order to understand how and why complexity arises in a computing universe, we must understand more about how the universe
processes information at its most fundamental scales. The way in which the universe computes is governed by the laws of physics.
Quantum mechanics is the branch of physical law that tells us how atoms and elementary particles behave, and how they process
information.
The most important thing to remember about quantum mechanics is that it is strange and counterintuitive. Quantum mechanics
is weird. Particles correspond to waves; waves are made up of particles; electrons and basketballs can be in two places at
once; elementary particles exhibit what Einstein called “spooky action at a distance.” Niels Bohr, one of the founders of
quantum mechanics, once said that anyone who can contemplate quantum mechanics without getting dizzy has not properly understood
it.
This intrinsically counterintuitive nature of quantum mechanics explains why many brilliant scientists, notably Einstein (who
received his Nobel prize for his work in quantum mechanics), have distrusted the field. More than others, Einstein had the
right to trust his intuition. Quantum mechanics contradicted his intuition, just as it contradicts everyone’s intuition. So Einstein thought
quantum mechanics could not be right: “God doesn’t play dice,” he declared. Einstein was wrong. God, or whoever it is who
is doing the playing, plays dice.
It is this intrinsically chancy nature of quantum mechanics that is the key to understanding the computing universe. The laws
of physics clearly support computation: I am writing these words on a computer. Moreover, physical law supports computation
at the most fundamental levels: Maxwell, Boltzmann, and Gibbs show that all atoms register and process information. My colleagues
and I exploit this information-processing ability of the universe to build quantum computers that store and process information
at the level of individual atoms. But who – or what – is programming this computing computer? Where do the bits of information
come from that tell the universe what to do? What is the source of all the variation and complexity that you see when you
look out your window? The answer lies in the throws of the quantum dice.
Let us look more closely at how quantum mechanics injects information into the universe. The laws of quantum mechanics are
largely deterministic: most of the time, each state gives rise to one, and only one, state at a later time. It is this deterministic
feature of quantum mechanics that allows the universe to behave like an ordinary digital computer, which processes information
in a deterministic fashion. Every now and then, however, an element of chance is injected into quantum evolution: when this
happens, a state can give rise probabilistically to several different possible states at a later time. The ability to give
rise to several different possible states allows the universe to behave like a quantum computer, which, unlike a conventional
digital computer, can follow several different computations simultaneously.
The mechanism by which quantum mechanics injects an element of chance into the operation of the universe is called “decoherence”
(Gell-Mann and Hartle, 1994). Decoherence effectively creates new bits of information, bits which previously did not exist. In other words, quantum mechanics, via decoherence,
is constantly injecting new bits of information into the world. Every detail that we see around us, every vein on a leaf,
every whorl on a fingerprint, every star in the sky, can be traced back to some bit that quantum mechanics created. Quantum
bits program the universe.
Now, however, there seems to be a problem. The laws of quantum mechanics imply that the new bits that decoherence injects
into the universe are essentially random, like the tosses of a fair coin: God plays dice. Surely, the universe did not arise
completely at random! The patterns that we see when we look out the window are far from random. On the contrary, although
detailed and complex, the information that we see around us is highly ordered. How can highly random bits give rise to a detailed,
complex, but orderly universe?
5.4 Typing monkeys
The computational ability of the universe supplies the answer to how random bits necessarily give rise to order and complexity.
To understand how the combination of randomness together with computation automatically gives rise to complexity, first look
at an old and incorrect explanation of the origin of order and complexity. Could the universe have originated from randomness
alone? No! Randomness, taken on its own, gives rise only to gibberish, not to structure. Random information, such as that
created by the repeated flipping of a coin, is highly unlikely to exhibit order and complexity.
The failure of randomness to exhibit order is embodied in the well-known image of monkeys typing on typewriters, created by
the French mathematician Emile Borel in the first decade of the twentieth century (Borel, 1909). Imagine a million typing monkeys (singes dactylographiques), each typing characters at random on a typewriter. Borel noted that these monkeys had a finite probability of producing
all the texts in all the richest libraries of the world. He then pointed out that the chance of them doing so was infinitesimally small. (This image has appeared again and again in popular
literature, as in the story that the monkeys immediately begin to type out Shakespeare’s Hamlet.)
To see how small a chance the monkeys have of producing any text of interest, imagine that every elementary particle in the
universe is a “monkey,” and that each particle has been flipping bits or “typing,” since the beginning of the universe. Elsewhere,
I have shown that the number of elementary events or bit flips that have occurred since the beginning of the universe is no
greater than 10120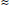 
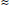2400. If one searches within this huge, random bit string for a specific substring (for example, Hamlet’s soliloquy), one can
show that the longest bit string that one can reasonably expect to find is no longer than the logarithm of the length of the
long, random string. In the case of the universe, the longest piece of Hamlet’s soliloquy one can expect to find is 400 bits
long. To encode a typewriter character such as a letter takes seven bits. In other words, if we ask the longest fraction of
Hamlet’s soliloquy that monkeys could have produced since the beginning of the universe, it is, “To be, or not to be – that
is the question: Whether ‘tis nobler … ” Monkeys, typing at random into typewriters, would not produce Hamlet, let alone the
complex world we see around us.
2400. If one searches within this huge, random bit string for a specific substring (for example, Hamlet’s soliloquy), one can
show that the longest bit string that one can reasonably expect to find is no longer than the logarithm of the length of the
long, random string. In the case of the universe, the longest piece of Hamlet’s soliloquy one can expect to find is 400 bits
long. To encode a typewriter character such as a letter takes seven bits. In other words, if we ask the longest fraction of
Hamlet’s soliloquy that monkeys could have produced since the beginning of the universe, it is, “To be, or not to be – that
is the question: Whether ‘tis nobler … ” Monkeys, typing at random into typewriters, would not produce Hamlet, let alone the
complex world we see around us.
Now suppose that, instead of typing on typewriters, the monkeys type their random strings of bits into computers. The computers
interpret each string as a program, a set of instructions to perform a particular computation. What then? At first it might
seem that random programs should give rise to random outputs: garbage in, garbage out, as computer scientists say. At second
glance, however, one finds that there are short, seemingly random programs that instruct the computer to do all kinds of interesting
things. (The probability that monkeys typing into a computer produce a given output is the subject of the branch of mathematics
called algorithmic information theory.) For example, there is a short program that instructs the computer to calculate the
digits of π, and a second program that instructs the computer to construct intricate fractal patterns. One of the shortest programs instructs the computer to compute
all possible mathematical theorems and patterns, including every pattern ever generated by the laws of physics! One might
say that the difference between monkeys typing into typewriters and monkeys typing into computers is all the difference in
the world.
To apply this purely mathematical construct of algorithmic information theory to our universe, we need two ingredients: a
computer, and monkeys. But we have a computer – the universe itself, which at its most microscopic level is busily processing
information. Where are the monkeys? As noted above, quantum mechanics provides the universe with a constant supply of fresh,
random bits, generated by the process of decoherence. Quantum fluctuations are the “monkeys” that program the universe (Lloyd,
2006).
To recapitulate:
(1) The mathematical theory of algorithmic information implies that a computer that is supplied with a random program has a good
chance of producing all the order and complexity that we see. This is simply a mathematical fact: to apply it to our universe
we need to identify the computing mechanism of the universe, together with its source of randomness.
(2) It has been known since the end of the nineteenth century that if the universe can be regarded as a machine (the mechanistic
paradigm), it is a machine that processes information. In the 1990s, I and other researchers in quantum computation showed
that the universe was capable of full-blown digital computation at its most microscopic levels: the universe is, technically,
a giant quantum computer.
(3) Quantum mechanics possesses intrinsic sources of randomness (God plays dice) that program this computer. As noted in the discussion
of the history of information-processing revolutions above, the injection of a few random bits, as in the case of genetic
mutation or recombination, can give rise to a radically new paradigm of information processing.
5.5 Discussion
The computational paradigm for the universe supplements the ordinary mechanistic paradigm: the universe is not just a machine,
it is a machine that processes information. The universe computes. The computing universe is not a metaphor, but a mathematical
fact: the universe is a physical system that can be programmed at its most microscopic level to perform universal digital
computation. Moreover, the universe is not just a computer: it is a quantum computer. Quantum mechanics is constantly injecting
fresh, random bits into the universe. Because of its computational nature, the universe processes and interprets those bits, naturally giving rise to all sorts of complex order and structure (Lloyd, 2006).
The results of the previous paragraphs are scientific results: they stem from the mathematics and physics of information processing.
Aristotle, when he had finished writing his Physics, wrote his Metaphysics: literally “the book after physics.” This chapter has discussed briefly the physics of the computing universe and its implications
for the origins of complexity and order. Let us use the physics of the computing universe as a basis for its metaphysics.
References
Borel, E. (1909). Éléments de la Théorie des Probalités. Paris: A. Hermann et Fils.
Chomsky, N., Hauser, M. D., and Tecumseh Fitch, W. (2002). The faculty of language: What is it, who has it, and how did it evolve. Science, 22(2): 1569–1579.
Chuang, I. A., and Nielsen, M. A. (2000). Quantum Computation and Quantum Information. Cambridge, UK: Cambridge University Press.
Ehrenfest, P., and Ehrenfest, T. (2002). The Conceptual Foundations of the Statistical Approach in Mechanics. New York: Dover.
Gell-Mann, M., and Hartle, J. B. (1994). The Physical Origins of Time Asymmetry, ed. J. Halliwell, J. Pérez-Mercader, and W. Zurek. Cambridge, UK: Cambridge University Press.
Lloyd, S. (2006). Programming the Universe. New York: Knopf.
Shannon, C. E., and Weaver, W. (1963). The Mathematical Theory of Communication. Urbana: University of Illinois Press.
Information and the Nature of Reality: From Physics to Metaphysics, eds. Paul Davies and Niels Henrik Gregersen. Published by Cambridge University Press © P. Davies and N. Gregersen 2010.