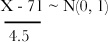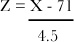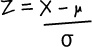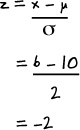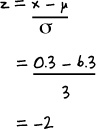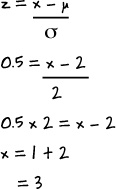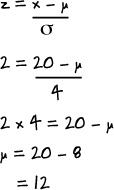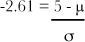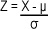Discrete data takes exact values...

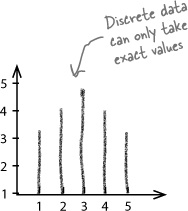
So far we’ve looked at probability distributions where the data is discrete. By this we mean the data is composed of distinct numeric values, and we’re been able to calculate the probability of each of these values. As an example, when we looked at the probability distribution for the winnings on a slot machine, the possible amounts we could win on each game were very precise. We knew exactly what amounts of money we could win, and we knew we’d win one of them.

If data is discrete, it’s numeric and can take only exact values. It’s often data that can be counted in some way, such as the number of gumballs in a gumball machine, the number of questions answered correctly in a game show, or the number of breakdowns in a particular period.

... but not all numeric data is discrete

It’s not always possible to say what all the values should be in a set of data. Sometimes data covers a range, where any value within that range is possible. As an example, suppose you were asked to accurately measure pieces of string that are between 10 inches and 11 inches long. You could have measurements of 10 inches, 10.1 inches, 10.01 inches, and so on, as the length could be anything within that range.

Numeric data like this is called continuous. It’s frequently data that is measured in some way rather than counted, and a lot depends on the degree of precision you need to measure to.

The type of data you have affects how you find probabilities.

So far we’ve only looked at probability distributions that deal with discrete data. Using these probability distributions, we’ve been able to find the probabilities of exact discrete values.

The problem is that a lot of real-world problems involve continuous data, and discrete probability distributions just don’t work with this sort of data. To find probabilities for continuous data, you need to know about continuous data and continuous probability distributions.

Meanwhile, someone has a problem...

What’s the delay?

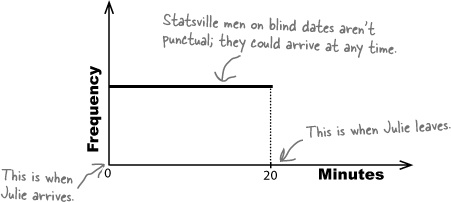
Julie is a student, and her best friend keeps trying to get her fixed up on blind dates in the hope that she’ll find that special someone. The only trouble is that not many of her dates are punctual—or indeed turn up.

Julie hates waiting alone for her date to arrive, so she’s made herself a rule: if her date hasn’t turned up after 20 minutes, then she leaves.

Here’s a sketch of the frequency showing the amount of time Julie spends waiting for her date to arrive:

Brain Power

We need to find probabilities for the amount of time Julie spends waiting for her date. Is the amount of time discrete or continuous? Why? How do you think we can go about finding probabilities?

We need a probability distribution for continuous data

We need to find the probability that Julie will have to wait for more than 5 minutes for her date to turn up. The trouble is, the amount of time Julie has to wait is continuous data, which means the probability distributions we’ve learned thus far don’t apply.

When we were dealing with discrete data, we were able to produce a specific probability distribution. We could do this by either showing the probability of each value in a table, or by specifying whether it followed a defined probability distribution, such as the binomial or Poisson distribution. By doing this, we were able to specify the probability of each possible value. As an example, when we found the probability distribution for the winnings per game for one of Fat Dan’s slot machines, we knew all of the possible values for the winnings and could calculate the probability of each one..

x	-1	4	9	14	19 Note With discrete data, we could give the probability of each value.
P(X = x)	0.977	0.008	0.008	0.006	0.001

For continuous data, it’s a different matter. We can no longer give the probability of each value because it’s impossible to say what each of these precise values is. As an example, Julie’s date might turn up after 4 minutes, 4 minutes 10 seconds, or 4 minutes 10.5 seconds. Counting the number of possible options would be impossible. Instead, we need to focus on a particular level of accuracy and the probability of getting a range of values.

Probability density functions can be used for continuous data

We can describe the probability distribution of a continuous random variable using a probability density function.

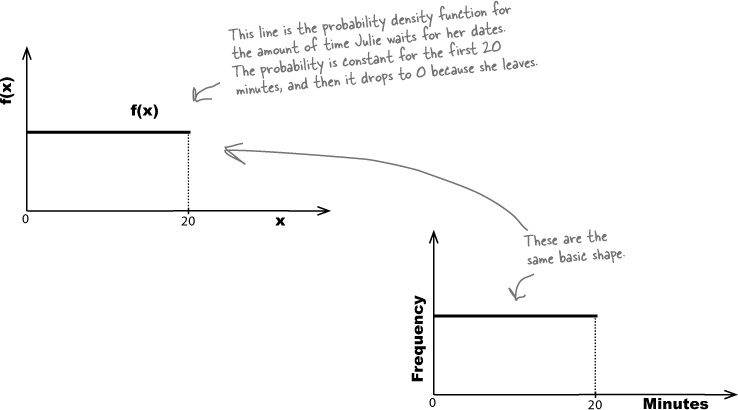
A probability density function f(x) is a function that you can use to find the probabilities of a continuous variable across a range of values. It tells us what the shape of the probability distribution is.

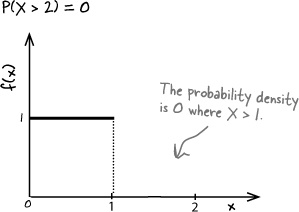
Here’s a sketch of the probability density function for the amount of time Julie spends waiting for her date to turn up:

Can you see how it matches the shape of the frequency? This isn’t just a coincidence.

Probability is all about how likely things are to happen, and the frequency tells you how often values occur. The higher the relative frequency, the higher the probability of that value occurring. As the frequency for the amount of time Julie has to wait is constant across the 20 minute period, this means that the probability density function is constant too.

Probability = area

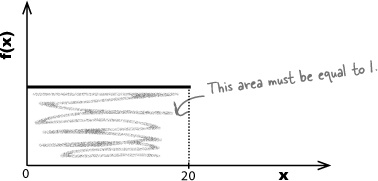
For continuous random variables, probabilities are given by area. To find the probability of getting a particular range of values, we start off by sketching the probability density function. The probability of getting a particular range of values is given by the area under the line between those values.

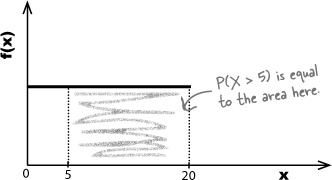
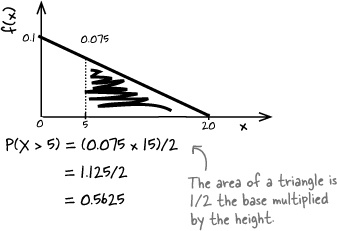
As an example, we want to find the probability that Julie has to wait for between 5 and 20 minutes for her date to turn up. We can find this probability by sketching the probability density function, and then working out the area under it where x is between 5 and 20.

The total area under the line must be equal to 1, as the total area represents the total probability. This is because for any probability distribution, the total probability must be equal to 1, and, therefore, the area must be too.

Let’s use this to help us find the probability that Julie will need to wait for over 5 minutes for her date to arrive.

Brain Power

The total area under the line must be 1. What’s the value of f(x)?

Hint: It’s a constant value.

To calculate probability, start by finding f(x)...

Before we can find probabilities for Julie, we need to find f(x), the probability density function.

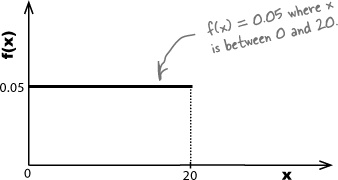
So far, we know that f(x) is a constant value, and we know that the total area under it must be equal to 1. If you look at the sketch of f(x), the area under it forms a rectangle where the width of the base is 20. If we can find the height of the rectangle, we’ll have the value of f(x).

We find the area of a rectangle by multiplying its width and height together. This means that

1	=	20 × height
height	=	1/20
	=	0.05

This means that f(x) must be equal to 0.05, as that ensures the total area under it will be 1. In other words,

f(x) = 0.05

where x between 0 and 20

Here’s a sketch:

Now that we’ve found the probability density function, we can find P(X > 5).

... then find probability by finding the area

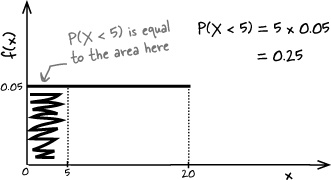
The area under the probability density line between 5 and 20 is a rectangle. This means that calculating the area of this rectangle will give us the probability P(X > 5).

P(X > 5)	=	(20 – 5) × 0.05
	=	0.75

Note

Area of rectangle = base x height.

So the probability that Julie will have to wait for more than 5 minutes is 0.75.

That doesn’t work for continuous probabilities.

For continuous probabilities, we have to find the probability by calculating the area under the probability density line.

We can’t add together the probability of getting each value within the range as there are an infinite number of values. It would take forever.

The only way we can find the probability for continuous probability distributions is to work out the area underneath the curve formed by the probability density function.

When dealing with continuous data, you calculate probabilities for a range of values.

We’ve found the probability

So far, we’ve looked at how you can use probability density functions to find probabilities for continuous data. We’ve found that the probability that Julie will have to wait for more than 5 minutes for her date to turn up is 0.75.

Searching for a soul sole mate

As well as preferring men who are punctual, Julie has preconceived ideas about what the love of her like should be like.

Julie loves wearing high-heeled shoes, and the higher the heel, the happier she is. The only problem is that she insists that her dates should be taller than her when she’s wearing her most extreme set of heels, and she’s running out of suitable men.

Unfortunately, the last couple of times Julie was sent on a blind date, the guys fell short of her expectations. She’s wondering how many men out there are taller than her and what the probability is that her dates will be tall enough for her high standards.

So how can we work out the probability this time?

Male modelling

So far we’ve looked at very simple continuous distributions, but it’s unlikely these will model the heights of the men Julie might be dating. It’s likely we’ll have several men who are quite a bit shorter than average, a few really tall ones, and a lot of men somewhere in between. We can expect most of the men to be average height.

Given this pattern, the probability density of the height of the men is likely to look something like this.

This shape of distribution is actually fairly common and can be applied to lots of situations. It’s called the normal distribution.

The normal distribution is an “ideal” model for continuous data

The normal distribution is called normal because it’s seen as an ideal. It’s what you’d “normally” expect to see in real life for a lot of continuous data such as measurements.

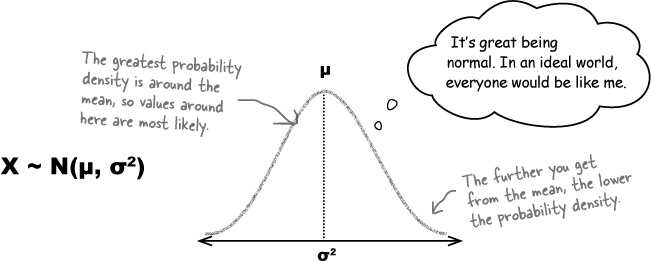
The normal distribution is in the shape of a bell curve. The curve is symmetrical, with the highest probability density in the center of the curve. The probability density decreases the further away you get from the mean. Both the mean and median are at the center and have the highest probability density.

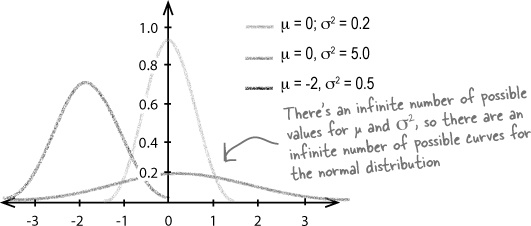
The normal distribution is defined by two parameters, μ and σ². μ tells you where the center of the curve is, and σ gives you the spread. If a continuous random variable X follows a normal distribution with mean μ and standard deviation σ, this is generally written X ~ N(μ, σ²).

So what effect do μ and σ really have on the shape of the normal distribution?

We said that μ tells you where the center of the curve is, and σ² indicates the spread of values. In practice, this means that as σ² gets larger, the flatter and wider the normal curve becomes.

No matter how far you go out on the graph, the probability density never equals 0.

The probability density gets closer and closer to 0, but never quite reaches it. If you looked at the probability density curve a very long way from μ, you’d find that the curve just skims above 0.

Another way of looking at this is that events become more and more unlikely to occur, but there’s always a tiny chance they might.

So how do we find normal probabilities?

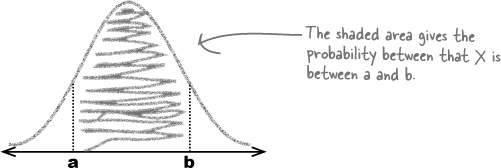
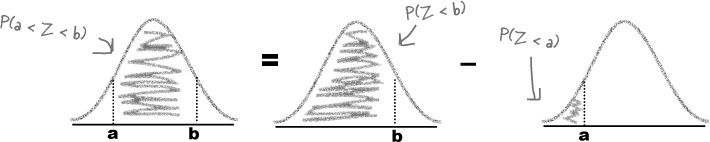
As with any other continuous probability distribution, you find probabilities by calculating the area under the curve of the distribution. The curve gives the probability density, and the probability is given by the area between particular ranges. If, for instance, you wanted to find the probability that a variable X lies between a and b, you’d need to find the area under the curve between points a and b.

Sound complicated? Don’t worry, it’s easier than you might think.

Working out the area under the normal curve would be difficult if you had to do it all by yourself, but fortunately you have a helping hand in the form of probability tables. All you need to do is work out the range of the area you want to find, and then look up the corresponding probability in the table.

Three steps to calculating normal probabilities

There are a few steps you need to take in order to find normal probabilities. We’ll guide you through the process, but for now here’s a roadmap of where we’re headed.

Step 1: Determine your distribution

The first thing we need to do is determine the distribution of the data.

Julie has been given the mean and standard deviation of the heights of eligible men in Statsville. The mean is 71 inches, and the variance is 20.25 inches. This means that if X represents the heights of the men, X ~ N(71, 20.25).

Note

This is shorthand for “The variable X follows a normal distribution, and has a mean of 71 and a variance of 20.25.”

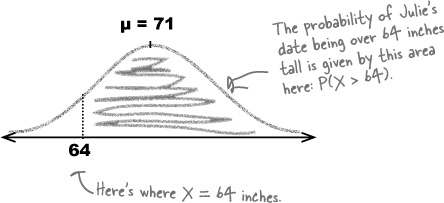
We also need to know which range of values will give us the right probability area. In this case, we need to find the probability that Julie’s blind date will be sufficiently tall.

Julie is 64 inches tall, so we’ll find the probability that her date is taller. Here’s a sketch:

Step 2: Standardize to N(0, 1)

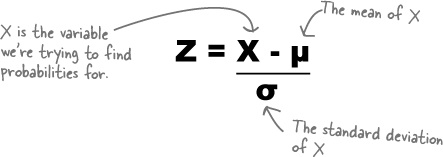
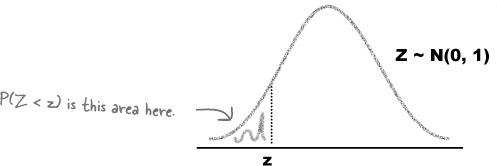
The next step is to standardize our variable X so that the mean becomes 0 and the standard deviation 1. This gives us a standardized normal variable Z where Z ~ N(0, 1).

Probability tables only give probabilities for N(0, 1).

Probability tables focus on giving the probabilities for N(0, 1) distributions, as it would be impossible to produce probability tables for every single normal distribution curve. There are an infinite number of possible values for μ and σ², and as the normal curve uses these as parameters to indicate the center and spread of the curve, there are also an infinite number of possible normal distribution curves.

Being able to use a standard normal distribution means that we can use the same set of probability tables for all possible values of μ and σ². There’s just one question—how do we convert out normal distribution into a standard form?

Brain Power

How do you think we might be able to standardize our normal distribution?

To standardize, first move the mean...

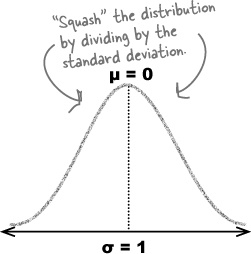
Let’s start off by transforming our normal distribution so that the mean becomes 0 rather than 71. To do this, we move the curve to the left by 71.

This gives us a new distribution of

X – 71 ~ N(0, 20.25)

... then squash the width

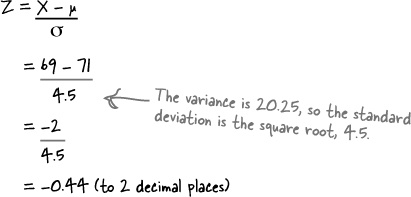
We also need to adjust the variance. To do this, we “squash” our distribution by dividing by the standard deviation. We know the variance is 20.25, so the standard deviation is 4.5.

Note

Recall that the standard deviation is the square root of the variance.

Doing this gives us

or Z ~ N(0, 1) where

Look familiar? This is the standard score we encountered when we first looked at the standard deviation in Chapter 3. In general, you can find the standard score for any normal variable X using

Now find Z for the specific value you want to find probability for

So far we’ve looked at how our probability distribution can be standardized to get from X ~ N(μ, σ²) to Z ~ N(0, 1). What we’re most interested in is actual probabilities. What we need to do is take the range of values we want to find probabilities for, and find the standard score of the limit of this range. Then we can look up the probability for our standard score using normal probability tables.

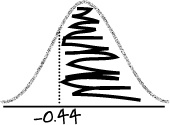
In our situation, we want to find the probability that Julie’s date is taller than her. Since Julie is 64 inches tall, we need to find P(X > 64). The limit of this range is 64, so if we calculate the standard score z of 64, we’ll be able to use this to find our probability.

Let’s find the standard score of 64.

So -1.56 is the standard score of 64, using the mean and standard deviation of the men’s heights in Statsville.

Now that we have this, we can move onto the final step, using tables to look up the probability.

Vital Statistics: Standard Score

To find the standard score of a value, use

Step 3: Look up the probability in your handy table

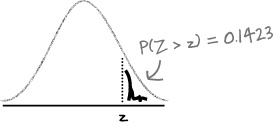
Now that we have a standard score, we can use probability tables to find our probability. Standard normal probability tables allow you to look up any value z, and then read off the corresponding probability P(Z < z).

Relax

We’ve put all the probability tables you need in Appendix B of the book.

Just flip to #1. Standard normal probabilities for the normal distribution tables you need to find probabilities in this chapter.

So how do you use probability tables?

Start off by calculating z to 2 decimal places. This is the value that you will need to look up in the table.

To look up the probability, you need to use the first column and the top row to find your value of z. The first column gives the value of z to 1 decimal place (without rounding), and the top row gives the second decimal place. The probability is where the two intersect.

As an example, if you wanted to find P(Z < –3.27), you’d find –3.2 in the first column, .07 in the top row, and read off a probability of 0.0005.

Julie’s probability is in the table

Let’s go back to our problem with Julie. We want to find P(Z > -1.56), so let’s look up -1.56 in the probability table and see what this gives us.

So, looking up the value of –1.56 in the probability table gives us a probability of 0.0594. In other words, P(Z < –1.56) = 0.0594. This means that

Note

The total probability is 1, so the total area under the curve is 1.

P(Z > –1.56)	=	1 – P(Z < –1.56)
	=	1 – 0.0594
	=	0.9406

In other words, the probability that Julie’s date is taller than her is 0.9406.

And they all lived happily ever after

Just as the odds predicted, Julie’s latest blind date was a success! Julie had to make sure her intended soulmate was compatible with her shoes, so she made sure she wore her highest heels to put him to the test. What’s more, he was already at the venue when she arrived, so she didn’t have to wait around.

But it doesn’t stop there.

Keep reading and we’ll show you more things you can do with the normal distribution. You’ve only just scratched the surface of what you can do.

Q:	Q: So there’s a function called the probability density function. What’s probability density?
A:	A: Probability density tells you how high probabilities are across ranges, and it’s described by the probability density function. It’s very similar to frequency density, which we encountered back in Chapter 1. Probability density uses area to tell you about probabilities, and frequency density uses area to tell you about frequencies.
Q:	Q: So aren’t probability density and probability the same thing?
A:	A: Probability density gives you a means of finding probability, but it’s not the probability itself. The probability density function is the line on the graph, and the probability is given by the area underneath it for a specific range of values.
Q:	Q: I see, so if you have a chart showing a probability density function, you find the probability by looking at area, instead of reading it directly off the chart.
A:	A: Exactly. For continuous data, you need to find probability by calculating area. Reading probabilities directly off a chart only works for discrete probabilities.
Q:	Q: Doesn’t finding the probability get complicated if you have to calculate areas? I mean, what if the probability density function is a curve and not a straight line?
A:	A: It’s still possible to do it, but you need to use calculus, which is why we’re not expecting you to do that in this book. The key thing is that you see where the probabilities come from and how to interpret them. If you’re really interested in working out probabilities using calculus, by all means, give it a go. We don’t want to hold you back.
Q:	Q: You’ve talked a lot about probability ranges. How do I find the probability of a precise value?
A:	A: When you’re dealing with continuous data, you’re really talking about acceptable degrees of accuracy, and you form a range based on these values. Let’s look at an example: Suppose you wanted a piece of string that’s 10 inches long to the nearest inch. It would be tempting to say that you need a piece of string that’s exactly 10 inches long, but that’s not entirely accurate. What you’re really after is a piece of string that’s between 9.5 inches and 10.5 inches, as you want string that 10 inches in length to the nearest inch. In other words, you want to find the probability of the length being in the range 9.5 inches to 10.5 inches.
Q:	Q: But what if I want to find the probability of a precise single value?
A:	A: This may not sound intuitive at first, but it’s actually 0. What you’re really talking about is the probability that you have a precise value to an infinite number of decimal places. If we go back to the string length example, what would happen if you needed a piece of string exactly 10 inches long? You would need to have a length of string measuring 10 inches long to the nearest atom and examined under a powerful microscope. The probability of the string being precisely 10 inches long is virtually impossible.
Q:	Q: But I’m sure that degree of accuracy isn’t needed. Surely it would be enough to measure it to the nearest hundredth of an inch?
A:	A: Ah, but that brings us back to the degree of accuracy you need in order for the length to pass as 10 inches, rather than finding the probability of a value to an infinite degree of precision. You use your degree of accuracy to construct your range of acceptable measurements so that you can work out the probability.

Q:	Q: Is this the same standard score that we saw before?
A:	A: Yes it is. It has more uses than just the normal distribution, but it’s particularly useful here as it allows us to use standard normal probability tables.
Q:	Q: Is the probability for my standardized range really the same as for my original distribution? How does that work?
A:	A: The probabilities work out the same, but using the probability tables is a lot more convenient. When we standardize our original normal distribution, everything keeps the same proportion. The overall area doesn’t grow or shrink, and as it’s area that gives the probability, the probability stays the same too.

Q:	Q: I’ve heard of the term “Gaussian.” What’s that?
A:	A: Another name for the normal distribution is the Gaussian distribution. If you hear someone talking about a Gaussian distribution, they’re talking about the same thing as the normal distribution.
Q:	Q: Are all normal probability tables the same?
A:	A: All normal probability tables give the same probabilities for your values. However, there’s some variation between tables as to what’s actually covered by them.
Q:	Q: Variation? What do you mean?
A:	A: Some tables and exam boards use different degrees of accuracy in their probability tables. Also, some show the tables in a slightly different format, but still give the same information.
Q:	Q: So what should I do if I’m taking a statistics exam?
A:	A: First of all, check what format of probability table will be available to you while you’re sitting the exam. Then, see if you can get a copy. Once you have a copy of the probability tables used by your exam board, spend time getting used to using them. That way you’ll be off to a flying start when the exam comes around.
Q:	Q: Finding the probability of a range looks kinda tricky. How do I do it?
A:	A: The big thing here is to think about how you can get the area you want using the probability tables. Probability tables generally only give probabilities in the form P(Z < z) where z is some value. The big trick, then, is to rewrite your probability only in these terms. If you’re dealing with a probability in the form P(a < Z < b)—that is, some sort of range—you’ll have two probabilities to look up, one for P(Z < a) and the other for P(Z < b). Once you have these probabilities, subtract the smallest from the largest.
Q:	Q: Do continuous distributions have a mode? Can you find the mode of the normal distribution?
A:	A: Yes. The mode of a continuous probability distribution is the value where the probability density is highest. If you draw the probability density, it’s the value of the highest point of the curve. If you look at the curve of the normal distribution, the highest point is in the middle. The mode of the normal distribution is μ.
Q:	Q: What about the median?
A:	A: The median of a continuous probability distribution is the value a where P(X < a) = 0.5. In other words, it’s the value that area of the probability density curve in half. For the normal distribution, the median is also μ. The median and mode don’t get used much when we’re dealing with continuous probability distributions. Expectation and variance are more important.
Q:	Q: What’s a standard score?
A:	A: The standard score of a variable is what you get if you subtract its mean and divide by its standard deviation. It’s a way of standardizing normal distributions so that they are transformed into a N(0, 1) distribution, and that gives you a way of comparing them. Standard scores are useful when you’re dealing with the normal distribution because it means you can look up the probability of a range using standard normal probability tables. The standard score of a particular value also describes how many standard deviations away from the mean the value is, which gives you an idea of its relative proximity to the mean.

P(–0.15 < Z < 0.5	P(Z < 0.5) – P(Z < –0.15)
	= 0.6915 – 0.4404
	= 0.2511

P(Z > –0.44)	= 1 – P(Z < –0.44)
	= 1 – 0.3300
	= 0.67

P(Z < z)	= 1 – 0.1423
	= 0.8577

1.8σ + 2.61σ =	15 – μ – 5 + μ
4.41σ =	10
σ =	2.27

1.8 × 2.27	= 15 – μ
λ	= 15 – 4.086
	= 10.914