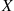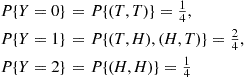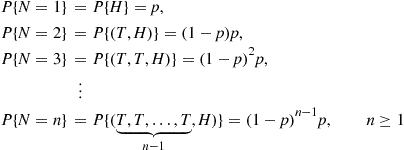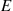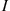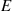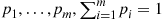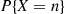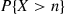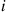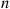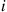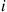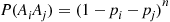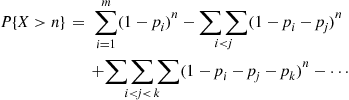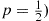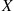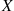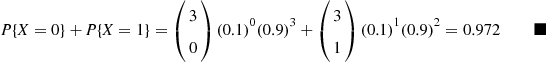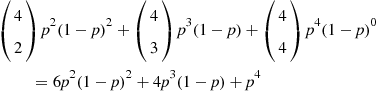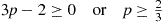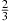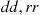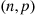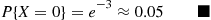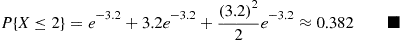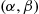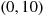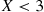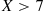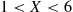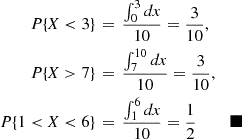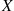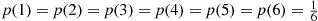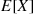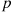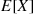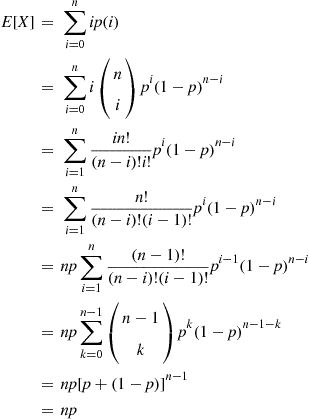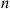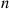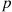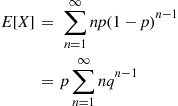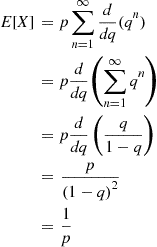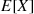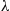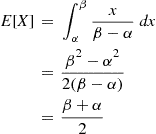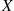Random Variables
Abstract
Random variables are quantities whose value is determined by the outcome of an experiment. This chapter introduces two types of random variables: discrete and continuous, and studies a variety of such of each type. The important idea of the expected value of a random variable is introduced.
Keywords
Discrete Random Variables; Continuous Random Variables; Binomial Random Variable; Poisson Random Variable; Geometric Random Variable; Uniform Random Variable; Exponential Random Variable; Expected Value; Variance; Joint Distributions
2.1 Random Variables
It frequently occurs that in performing an experiment we are mainly interested in some functions of the outcome as opposed to the outcome itself. For instance, in tossing dice we are often interested in the sum of the two dice and are not really concerned about the actual outcome. That is, we may be interested in knowing that the sum is seven and not be concerned over whether the actual outcome was (1, 6) or (2, 5) or (3, 4) or (4, 3) or (5, 2) or (6, 1). These quantities of interest, or more formally, these real-valued functions defined on the sample space, are known as random variables.
Since the value of a random variable is determined by the outcome of the experiment, we may assign probabilities to the possible values of the random variable.
In all of the preceding examples, the random variables of interest took on either a finite or a countable number of possible values.* Such random variables are called discrete. However, there also exist random variables that take on a continuum of possible values. These are known as continuous random variables. One example is the random variable denoting the lifetime of a car, when the car’s lifetime is assumed to take on any value in some interval (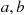 ).
).
The cumulative distribution function (cdf) (or more simply the distribution function)  of the random variable
of the random variable 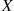 is defined for any real number
is defined for any real number 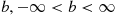 , by
, by
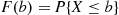
In words, 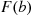 denotes the probability that the random variable
denotes the probability that the random variable  takes on a value that is less than or equal to
takes on a value that is less than or equal to 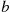 . Some properties of the cdf
. Some properties of the cdf  are
are
Property (i) follows since for 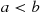 the event
the event 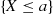 is contained in the event
is contained in the event 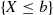 , and so it must have a smaller probability. Properties (ii) and (iii) follow since
, and so it must have a smaller probability. Properties (ii) and (iii) follow since 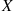 must take on some finite value.
must take on some finite value.
All probability questions about 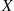 can be answered in terms of the cdf
can be answered in terms of the cdf  . For example,
. For example,
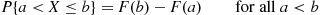
This follows since we may calculate 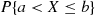 by first computing the probability that
by first computing the probability that 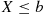 (that is,
(that is, 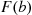 ) and then subtracting from this the probability that
) and then subtracting from this the probability that  (that is,
(that is,  ).
).
If we desire the probability that  is strictly smaller than
is strictly smaller than  , we may calculate this probability by
, we may calculate this probability by

where 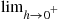 means that we are taking the limit as
means that we are taking the limit as 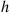 decreases to 0. Note that
decreases to 0. Note that  does not necessarily equal
does not necessarily equal 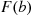 since
since 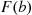 also includes the probability that
also includes the probability that  equals
equals 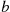 .
.
2.2 Discrete Random Variables
As was previously mentioned, a random variable that can take on at most a countable number of possible values is said to be discrete. For a discrete random variable 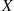 , we define the probability mass function
, we define the probability mass function  of
of  by
by
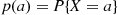
The probability mass function 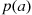 is positive for at most a countable number of values of
is positive for at most a countable number of values of  . That is, if
. That is, if  must assume one of the values
must assume one of the values 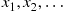 then
then

Since  must take on one of the values
must take on one of the values  , we have
, we have
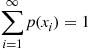
The cumulative distribution function 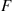 can be expressed in terms of
can be expressed in terms of  by
by
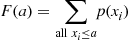
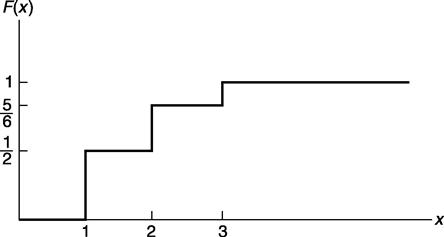
For instance, suppose  has a probability mass function given by
has a probability mass function given by
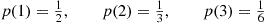
then, the cumulative distribution function  of
of 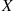 is given by
is given by

This is graphically presented in Figure 2.1.
Discrete random variables are often classified according to their probability mass functions. We now consider some of these random variables.
2.2.1 The Bernoulli Random Variable
Suppose that a trial, or an experiment, whose outcome can be classified as either a “success” or as a “failure” is performed. If we let  equal 1 if the outcome is a success and 0 if it is a failure, then the probability mass function of
equal 1 if the outcome is a success and 0 if it is a failure, then the probability mass function of 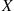 is given by
is given by
 (2.2)
(2.2)where 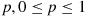 , is the probability that the trial is a “success.”
, is the probability that the trial is a “success.”
A random variable 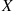 is said to be a Bernoulli random variable if its probability mass function is given by Equation (2.2) for some
is said to be a Bernoulli random variable if its probability mass function is given by Equation (2.2) for some  .
.
2.2.2 The Binomial Random Variable
Suppose that 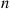 independent trials, each of which results in a “success” with probability
independent trials, each of which results in a “success” with probability 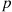 and in a “failure” with probability
and in a “failure” with probability  , are to be performed. If
, are to be performed. If  represents the number of successes that occur in the
represents the number of successes that occur in the  trials, then
trials, then 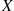 is said to be a binomial random variable with parameters
is said to be a binomial random variable with parameters 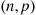 .
.
The probability mass function of a binomial random variable having parameters  is given by
is given by
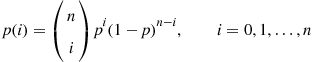 (2.3)
(2.3)where
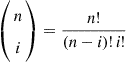
equals the number of different groups of 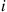 objects that can be chosen from a set of
objects that can be chosen from a set of 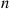 objects. The validity of Equation (2.3) may be verified by first noting that the probability of any particular sequence of the
objects. The validity of Equation (2.3) may be verified by first noting that the probability of any particular sequence of the 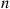 outcomes containing
outcomes containing 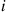 successes and
successes and  failures is, by the assumed independence of trials,
failures is, by the assumed independence of trials, 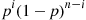 . Equation (2.3) then follows since there are
. Equation (2.3) then follows since there are  different sequences of the
different sequences of the  outcomes leading to
outcomes leading to 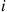 successes and
successes and  failures. For instance, if
failures. For instance, if  , then there are
, then there are  ways in which the three trials can result in two successes. Namely, any one of the three outcomes
ways in which the three trials can result in two successes. Namely, any one of the three outcomes 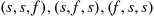 , where the outcome
, where the outcome 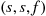 means that the first two trials are successes and the third a failure. Since each of the three outcomes
means that the first two trials are successes and the third a failure. Since each of the three outcomes 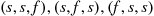 has a probability
has a probability 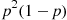 of occurring the desired probability is thus
of occurring the desired probability is thus  .
.
Note that, by the binomial theorem, the probabilities sum to one, that is,
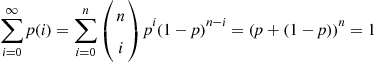
2.2.3 The Geometric Random Variable
Suppose that independent trials, each having probability 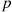 of being a success, are performed until a success occurs. If we let
of being a success, are performed until a success occurs. If we let 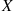 be the number of trials required until the first success, then
be the number of trials required until the first success, then 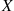 is said to be a geometric random variable with parameter
is said to be a geometric random variable with parameter  . Its probability mass function is given by
. Its probability mass function is given by
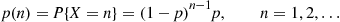 (2.4)
(2.4)Equation (2.4) follows since in order for  to equal
to equal 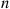 it is necessary and sufficient that the first
it is necessary and sufficient that the first  trials be failures and the nth trial a success. Equation (2.4) follows since the outcomes of the successive trials are assumed to be independent.
trials be failures and the nth trial a success. Equation (2.4) follows since the outcomes of the successive trials are assumed to be independent.
To check that 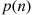 is a probability mass function, we note that
is a probability mass function, we note that
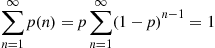
2.2.4 The Poisson Random Variable
A random variable 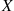 , taking on one of the values
, taking on one of the values  , is said to be a Poisson random variable with parameter
, is said to be a Poisson random variable with parameter  , if for some
, if for some  ,
,
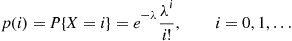 (2.5)
(2.5)Equation (2.5) defines a probability mass function since
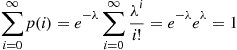
The Poisson random variable has a wide range of applications in a diverse number of areas, as will be seen in Chapter 5.
An important property of the Poisson random variable is that it may be used to approximate a binomial random variable when the binomial parameter 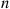 is large and
is large and  is small. To see this, suppose that
is small. To see this, suppose that  is a binomial random variable with parameters
is a binomial random variable with parameters 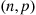 , and let
, and let 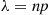 . Then
. Then

Now, for  large and
large and  small
small

Hence, for 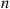 large and
large and 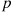 small,
small,

2.3 Continuous Random Variables
In this section, we shall concern ourselves with random variables whose set of possible values is uncountable. Let 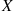 be such a random variable. We say that
be such a random variable. We say that  is a continuous random variable if there exists a nonnegative function
is a continuous random variable if there exists a nonnegative function 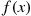 , defined for all real
, defined for all real 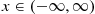 , having the property that for any set
, having the property that for any set  of real numbers
of real numbers
 (2.6)
(2.6)The function  is called the probability density function of the random variable
is called the probability density function of the random variable  .
.
In words, Equation (2.6) states that the probability that  will be in
will be in 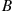 may be obtained by integrating the probability density function over the set
may be obtained by integrating the probability density function over the set 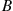 . Since
. Since 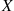 must assume some value,
must assume some value, 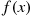 must satisfy
must satisfy

All probability statements about  can be answered in terms of
can be answered in terms of 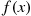 . For instance, letting
. For instance, letting  , we obtain from Equation (2.6) that
, we obtain from Equation (2.6) that
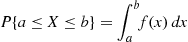 (2.7)
(2.7)
If we let 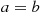 in the preceding, then
in the preceding, then

In words, this equation states that the probability that a continuous random variable will assume any particular value is zero.
The relationship between the cumulative distribution 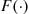 and the probability density
and the probability density 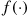 is expressed by
is expressed by

Differentiating both sides of the preceding yields

That is, the density is the derivative of the cumulative distribution function. A somewhat more intuitive interpretation of the density function may be obtained from Equation (2.7) as follows:
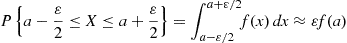
when  is small. In other words, the probability that
is small. In other words, the probability that  will be contained in an interval of length
will be contained in an interval of length  around the point
around the point  is approximately
is approximately  . From this, we see that
. From this, we see that  is a measure of how likely it is that the random variable will be near
is a measure of how likely it is that the random variable will be near  .
.
There are several important continuous random variables that appear frequently in probability theory. The remainder of this section is devoted to a study of certain of these random variables.
2.3.1 The Uniform Random Variable
A random variable is said to be uniformly distributed over the interval 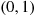 if its probability density function is given by
if its probability density function is given by

Note that the preceding is a density function since  and
and
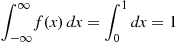
Since  only when
only when 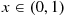 , it follows that
, it follows that 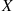 must assume a value in
must assume a value in 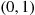 . Also, since
. Also, since 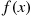 is constant for
is constant for 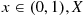 is just as likely to be “near” any value in (0, 1) as any other value. To check this, note that, for any
is just as likely to be “near” any value in (0, 1) as any other value. To check this, note that, for any 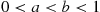 ,
,
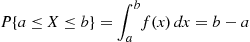
In other words, the probability that 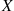 is in any particular subinterval of
is in any particular subinterval of 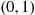 equals the length of that subinterval.
equals the length of that subinterval.
In general, we say that 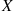 is a uniform random variable on the interval
is a uniform random variable on the interval 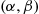 if its probability density function is given by
if its probability density function is given by
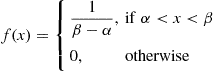 (2.8)
(2.8)2.3.2 Exponential Random Variables
A continuous random variable whose probability density function is given, for some 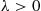 , by
, by
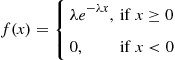
is said to be an exponential random variable with parameter 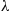 . These random variables will be extensively studied in Chapter 5, so we will content ourselves here with just calculating the cumulative distribution function
. These random variables will be extensively studied in Chapter 5, so we will content ourselves here with just calculating the cumulative distribution function 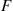 :
:

Note that 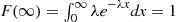 , as, of course, it must.
, as, of course, it must.
2.3.3 Gamma Random Variables
A continuous random variable whose density is given by

for some 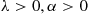 is said to be a gamma random variable with parameters
is said to be a gamma random variable with parameters  . The quantity
. The quantity  ) is called the gamma function and is defined by
) is called the gamma function and is defined by

It is easy to show by induction that for integral 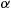 , say,
, say,  ,
,
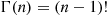
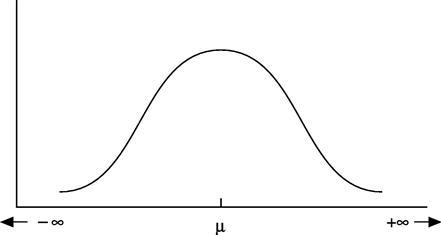
2.3.4 Normal Random Variables
We say that  is a normal random variable (or simply that
is a normal random variable (or simply that 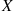 is normally distributed) with parameters
is normally distributed) with parameters 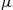 and
and  if the density of
if the density of  is given by
is given by

This density function is a bell-shaped curve that is symmetric around 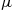 (see Figure 2.2).
(see Figure 2.2).
An important fact about normal random variables is that if 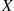 is normally distributed with parameters
is normally distributed with parameters 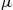 and
and 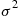 then
then 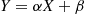 is normally distributed with parameters
is normally distributed with parameters 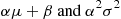 . To prove this, suppose first that
. To prove this, suppose first that  and note that
and note that 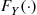 *, the cumulative distribution function of the random variable
*, the cumulative distribution function of the random variable 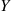 , is given by
, is given by
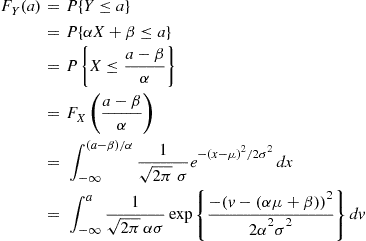 (2.9)
(2.9)
where the last equality is obtained by the change in variables 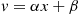 . However, since
. However, since  , it follows from Equation (2.9) that the probability density function
, it follows from Equation (2.9) that the probability density function  is given by
is given by
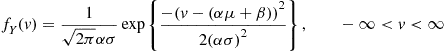
Hence,  is normally distributed with parameters
is normally distributed with parameters 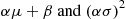 . A similar result is also true when
. A similar result is also true when 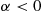 .
.
One implication of the preceding result is that if 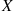 is normally distributed with parameters
is normally distributed with parameters  then
then 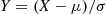 is normally distributed with parameters 0 and 1. Such a random variable
is normally distributed with parameters 0 and 1. Such a random variable 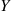 is said to have the standard or unit normal distribution.
is said to have the standard or unit normal distribution.
2.4 Expectation of a Random Variable
2.4.1 The Discrete Case
If  is a discrete random variable having a probability mass function
is a discrete random variable having a probability mass function  , then the expected value of
, then the expected value of  is defined by
is defined by

In other words, the expected value of 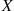 is a weighted average of the possible values that
is a weighted average of the possible values that 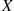 can take on, each value being weighted by the probability that
can take on, each value being weighted by the probability that 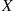 assumes that value. For example, if the probability mass function of
assumes that value. For example, if the probability mass function of 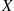 is given by
is given by
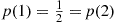
then

is just an ordinary average of the two possible values 1 and 2 that 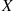 can assume. On the other hand, if
can assume. On the other hand, if

then
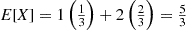
is a weighted average of the two possible values 1 and 2 where the value 2 is given twice as much weight as the value 1 since 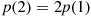 .
.
2.4.2 The Continuous Case
We may also define the expected value of a continuous random variable. This is done as follows. If  is a continuous random variable having a probability density function
is a continuous random variable having a probability density function  , then the expected value of
, then the expected value of 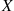 is defined by
is defined by