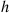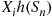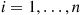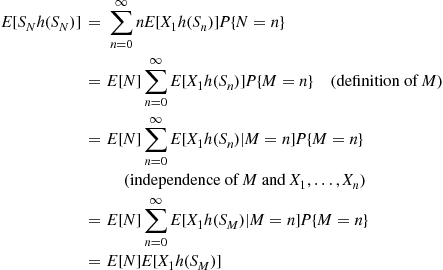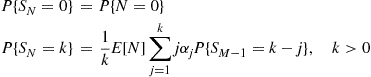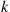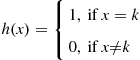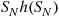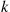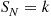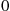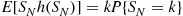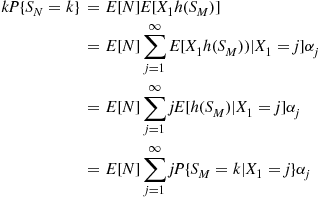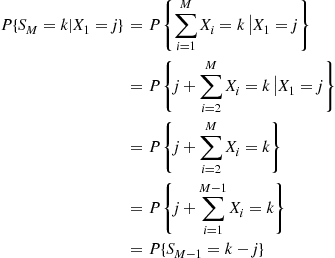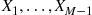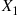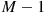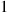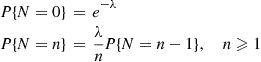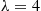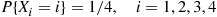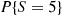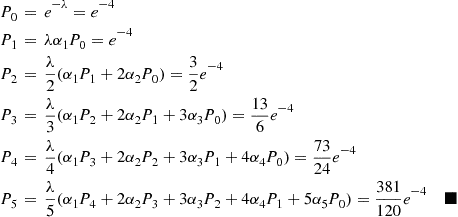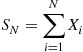
is said to be a compound random variable, with the distribution of 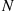 called the compounding distribution. In this subsection we will first derive an identity involving such random variables. We will then specialize to where the
called the compounding distribution. In this subsection we will first derive an identity involving such random variables. We will then specialize to where the 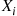 are positive integer valued random variables, prove a corollary of the identity, and then use this corollary to develop a recursive formula for the probability mass function of
are positive integer valued random variables, prove a corollary of the identity, and then use this corollary to develop a recursive formula for the probability mass function of 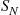 , for a variety of common compounding distributions.
, for a variety of common compounding distributions.
To begin, let 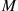 be a random variable that is independent of the sequence
be a random variable that is independent of the sequence 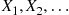 , and which is such that
, and which is such that

Suppose now that the  are positive integer valued random variables, and let
are positive integer valued random variables, and let
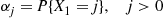
The successive values of 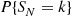 can often be obtained from the following corollary to Proposition 3.5.
can often be obtained from the following corollary to Proposition 3.5.
When the distributions of 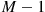 and
and 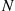 are related, the preceding corollary can be a useful recursion for computing the probability mass function of
are related, the preceding corollary can be a useful recursion for computing the probability mass function of 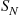 , as is illustrated in the following subsections.
, as is illustrated in the following subsections.
3.7.1 Poisson Compounding Distribution
If 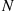 is the Poisson distribution with mean
is the Poisson distribution with mean 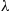 , then
, then
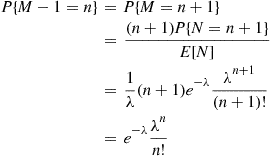
Consequently, 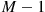 is also Poisson with mean
is also Poisson with mean 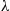 . Thus, with
. Thus, with
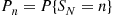
the recursion given by Corollary 3.6 can be written
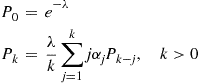
3.7.2 Binomial Compounding Distribution
Suppose that 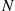 is a binomial random variable with parameters
is a binomial random variable with parameters  and
and 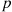 . Then,
. Then,
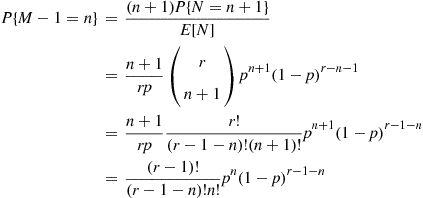
Thus, 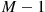 is a binomial random variable with parameters
is a binomial random variable with parameters 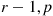 .
.
Fixing 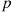 , let
, let 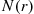 be a binomial random variable with parameters
be a binomial random variable with parameters  and
and 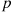 , and let
, and let
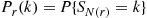
Then, Corollary 3.6 yields
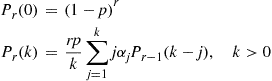
For instance, letting 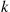 equal
equal 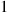 , then
, then 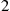 , and then
, and then 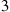 gives
gives
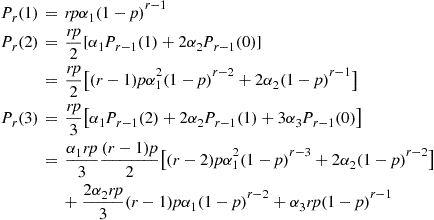
3.7.3 A Compounding Distribution Related to the Negative Binomial
Suppose, for a fixed value of 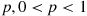 , the compounding random variable
, the compounding random variable 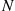 has a probability mass function
has a probability mass function

Such a random variable can be thought of as being the number of failures that occur before a total of  successes have been amassed when each trial is independently a success with probability
successes have been amassed when each trial is independently a success with probability 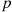 . (There will be
. (There will be 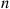 such failures if the
such failures if the  th success occurs on trial
th success occurs on trial  . Consequently,
. Consequently,  is a negative binomial random variable with parameters
is a negative binomial random variable with parameters  and
and 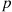 .) Using that the mean of the negative binomial random variable
.) Using that the mean of the negative binomial random variable  is
is 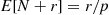 , we see that
, we see that 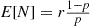 .
.
Regard 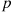 as fixed, and call
as fixed, and call 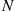 an NB(
an NB( ) random variable. The random variable
) random variable. The random variable 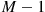 has probability mass function
has probability mass function

In other words,  is an
is an 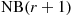 random variable.
random variable.
Letting, for an NB( ) random variable
) random variable 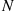 ,
,
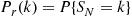
Corollary 3.6 yields
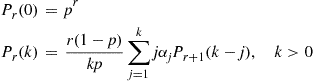
Thus,
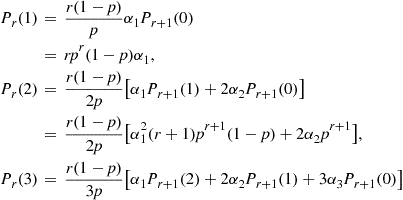
and so on.
Exercises
1. If  and
and 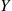 are both discrete, show that
are both discrete, show that 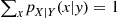 for all
for all 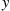 such that
such that 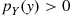 .
.
*2. Let 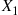 and
and 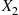 be independent geometric random variables having the same parameter
be independent geometric random variables having the same parameter 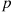 . Guess the value of
. Guess the value of
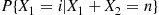
Hint: Suppose a coin having probability 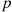 of coming up heads is continually flipped. If the second head occurs on flip number
of coming up heads is continually flipped. If the second head occurs on flip number 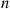 , what is the conditional probability that the first head was on flip number
, what is the conditional probability that the first head was on flip number  ?
?
Verify your guess analytically.
3. The joint probability mass function of 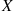 and
and 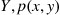 , is given by
, is given by
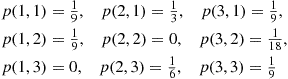
Compute 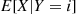 for
for 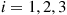 .
.
4. In Exercise 3, are the random variables 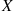 and
and 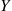 independent?
independent?
5. An urn contains three white, six red, and five black balls. Six of these balls are randomly selected from the urn. Let 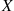 and
and 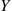 denote respectively the number of white and black balls selected. Compute the conditional probability mass function of
denote respectively the number of white and black balls selected. Compute the conditional probability mass function of 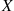 given that
given that 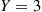 . Also compute
. Also compute 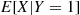 .
.
*6. Repeat Exercise 5 but under the assumption that when a ball is selected its color is noted, and it is then replaced in the urn before the next selection is made.
7. Suppose 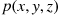 , the joint probability mass function of the random variables
, the joint probability mass function of the random variables 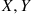 , and
, and 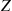 , is given by
, is given by
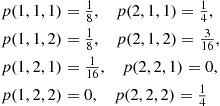
What is 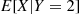 ? What is
? What is 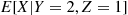 ?
?
8. An unbiased die is successively rolled. Let 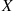 and
and 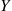 denote, respectively, the number of rolls necessary to obtain a six and a five. Find (a)
denote, respectively, the number of rolls necessary to obtain a six and a five. Find (a) 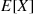 , (b)
, (b) 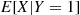 , (c)
, (c) 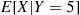 .
.
9. Show in the discrete case that if 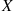 and
and 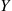 are independent, then
are independent, then
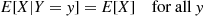
10. Suppose 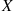 and
and  are independent continuous random variables. Show that
are independent continuous random variables. Show that
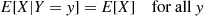
11. The joint density of  and
and  is
is
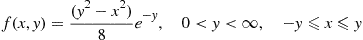
Show that 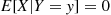 .
.
12. The joint density of 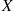 and
and 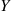 is given by
is given by

Show 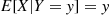 .
.
*13. Let 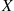 be exponential with mean
be exponential with mean 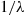 ; that is,
; that is,