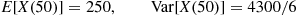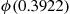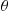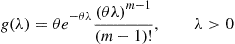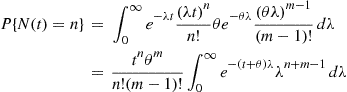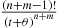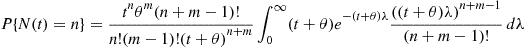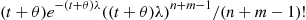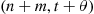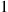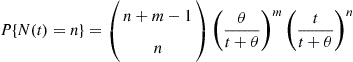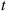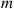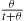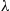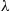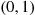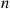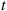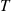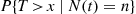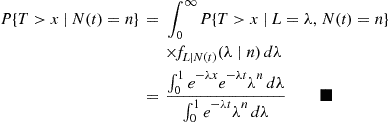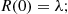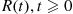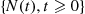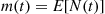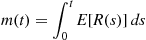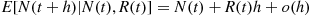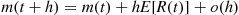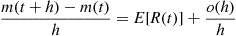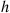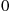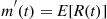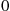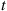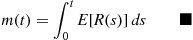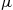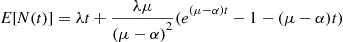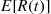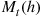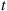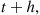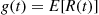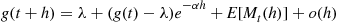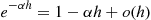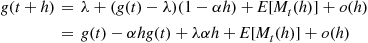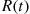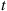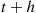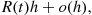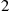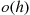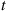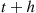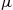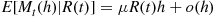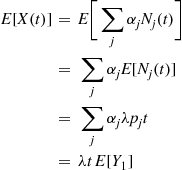
Also,

where the next to last equality follows since the variance of the Poisson random variable 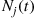 is equal to its mean.
is equal to its mean.
Thus, we see that the representation (5.26) results in the same expressions for the mean and variance of 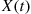 as were previously derived.
as were previously derived.
One of the uses of the representation (5.26) is that it enables us to conclude that as 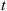 grows large, the distribution of
grows large, the distribution of 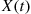 converges to the normal distribution. To see why, note first that it follows by the central limit theorem that the distribution of a Poisson random variable converges to a normal distribution as its mean increases. (Why is this?) Therefore, each of the random variables
converges to the normal distribution. To see why, note first that it follows by the central limit theorem that the distribution of a Poisson random variable converges to a normal distribution as its mean increases. (Why is this?) Therefore, each of the random variables 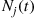 converges to a normal random variable as
converges to a normal random variable as 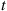 increases. Because they are independent, and because the sum of independent normal random variables is also normal, it follows that
increases. Because they are independent, and because the sum of independent normal random variables is also normal, it follows that 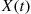 also approaches a normal distribution as
also approaches a normal distribution as 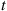 increases.
increases.
Another useful result is that if 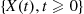 and
and  are independent compound Poisson processes with respective Poisson parameters and distributions
are independent compound Poisson processes with respective Poisson parameters and distributions 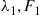 and
and  , then
, then 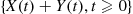 is also a compound Poisson process. This is true because in this combined process events will occur according to a Poisson process with rate
is also a compound Poisson process. This is true because in this combined process events will occur according to a Poisson process with rate 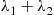 , and each event independently will be from the first compound Poisson process with probability
, and each event independently will be from the first compound Poisson process with probability 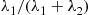 . Consequently, the combined process will be a compound Poisson process with Poisson parameter
. Consequently, the combined process will be a compound Poisson process with Poisson parameter 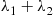 , and with distribution function
, and with distribution function 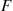 given by
given by
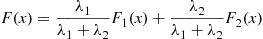
5.4.3 Conditional or Mixed Poisson Processes
Let 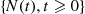 be a counting process whose probabilities are defined as follows. There is a positive random variable
be a counting process whose probabilities are defined as follows. There is a positive random variable 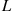 such that, conditional on
such that, conditional on 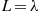 , the counting process is a Poisson process with rate
, the counting process is a Poisson process with rate 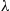 . Such a counting process is called a conditional or a mixed Poisson process.
. Such a counting process is called a conditional or a mixed Poisson process.
Suppose that 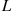 is continuous with density function
is continuous with density function 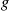 . Because
. Because
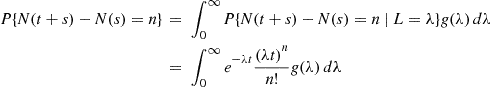 (5.27)
(5.27)we see that a conditional Poisson process has stationary increments. However, because knowing how many events occur in an interval gives information about the possible value of 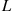 , which affects the distribution of the number of events in any other interval, it follows that a conditional Poisson process does not generally have independent increments. Consequently, a conditional Poisson process is not generally a Poisson process.
, which affects the distribution of the number of events in any other interval, it follows that a conditional Poisson process does not generally have independent increments. Consequently, a conditional Poisson process is not generally a Poisson process.
To compute the mean and variance of 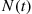 , condition on
, condition on  . Because, conditional on
. Because, conditional on 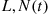 is Poisson with mean
is Poisson with mean 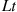 , we obtain
, we obtain
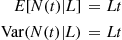
where the final equality used that the variance of a Poisson random variable is equal to its mean. Consequently, the conditional variance formula yields
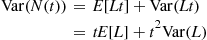
We can compute the conditional distribution function of  , given that
, given that  , as follows.
, as follows.
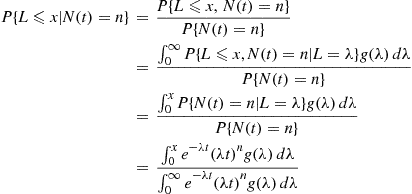
where the final equality used Equation (5.27). In other words, the conditional density function of  given that
given that 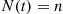 is
is
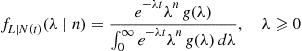 (5.28)
(5.28)
There is a nice formula for the probability that more than 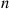 events occur in an interval of length
events occur in an interval of length 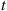 . In deriving it we will use the identity
. In deriving it we will use the identity
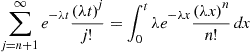 (5.29)
(5.29)
which follows by noting that it equates the probability that the number of events by time 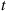 of a Poisson process with rate
of a Poisson process with rate 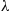 is greater than
is greater than 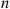 with the probability that the time of the
with the probability that the time of the 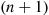 st event of this process (which has a gamma
st event of this process (which has a gamma 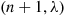 distribution) is less than
distribution) is less than 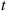 . Interchanging
. Interchanging 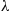 and
and 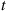 in Equation (5.29) yields the equivalent identity
in Equation (5.29) yields the equivalent identity
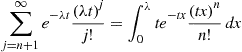 (5.30)
(5.30)
Using Equation (5.27) we now have
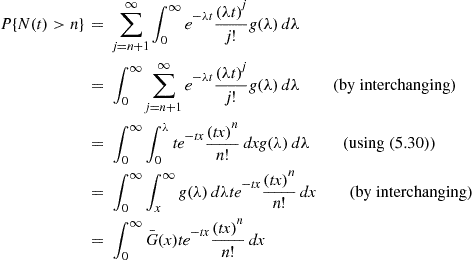
5.5 Random Intensity Functions and Hawkes Processes
Whereas the intensity function 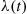 of a nonhomogeneous Poisson process is a deterministic function, there are counting processes
of a nonhomogeneous Poisson process is a deterministic function, there are counting processes 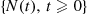 whose intensity function value at time
whose intensity function value at time 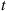 , call it
, call it 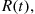 is a random variable whose value depends on the history of the process up to time
is a random variable whose value depends on the history of the process up to time 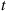 . That is, if we let
. That is, if we let 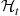 denote the “history” of the process up to time
denote the “history” of the process up to time  then
then 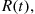 the intensity rate at time
the intensity rate at time 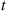 , is a random variable whose value is determined by
, is a random variable whose value is determined by 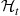 and which is such that
and which is such that
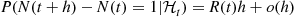
and
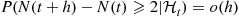
The Hawkes process is an example of a counting process having a random intensity function. This counting process assumes that there is a base intensity value 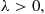 and that associated with each event is a nonnegative random variable, called a mark, whose value is independent of all that has previously occurred and has distribution
and that associated with each event is a nonnegative random variable, called a mark, whose value is independent of all that has previously occurred and has distribution 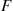 . Whenever an event occurs, it is supposed that the current value of the random intensity function increases by the amount of the event’s mark, with this increase decreasing over time at an exponential rate
. Whenever an event occurs, it is supposed that the current value of the random intensity function increases by the amount of the event’s mark, with this increase decreasing over time at an exponential rate  . More specifically, if there have been a total of
. More specifically, if there have been a total of 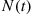 events by time
events by time 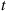 , with
, with 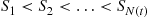 being the event times and
being the event times and  being the mark of event
being the mark of event  then
then
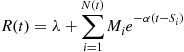
In other words, a Hawkes process is a counting process in which
2. whenever an event occurs, the random intensity increases by the value of the event’s mark;
3. if there are no events between  and
and  then
then 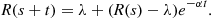
Because the intensity increases each time an event occurs, the Hawkes process is said to be a self-exciting process.
We will derive  the expected number of events of a Hawkes process that occur by time
the expected number of events of a Hawkes process that occur by time  . To do so, we will need the following lemma, which is valid for all counting processes.
. To do so, we will need the following lemma, which is valid for all counting processes.