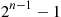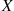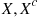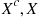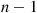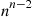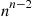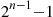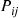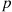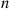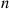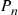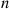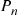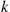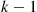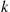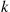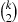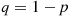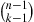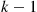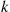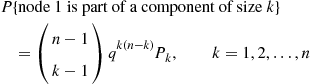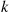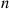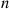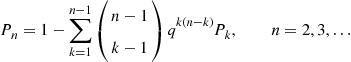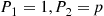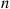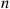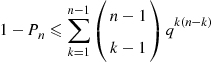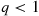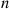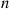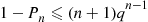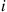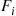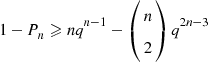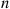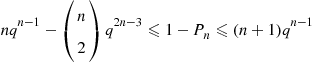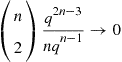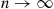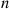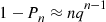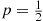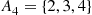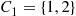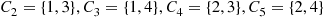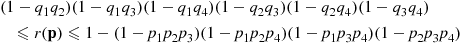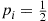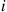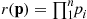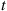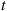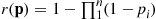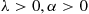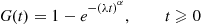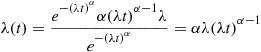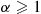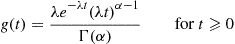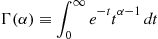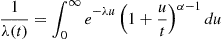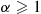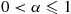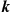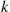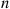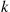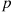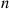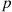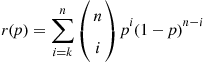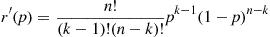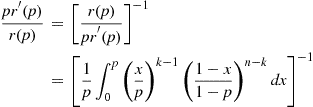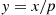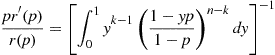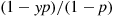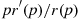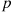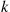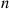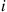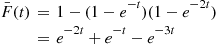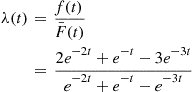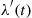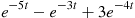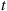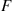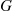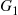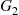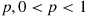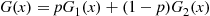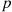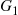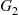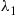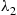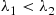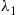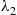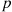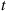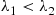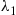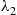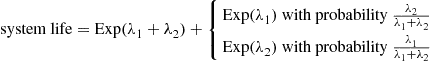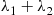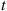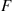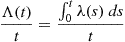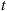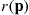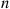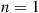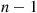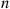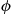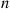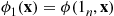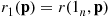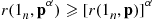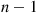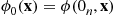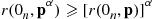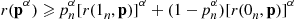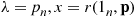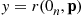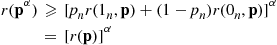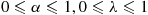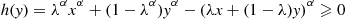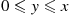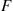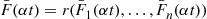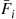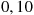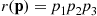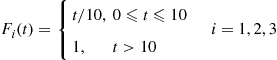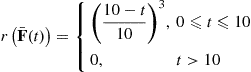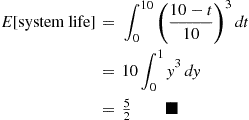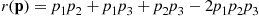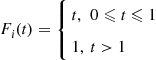9.5 System Life as a Function of Component Lives
For a random variable having distribution function G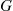 , we define G¯(a)≡1-G(a)
, we define G¯(a)≡1-G(a) to be the probability that the random variable is greater than a
to be the probability that the random variable is greater than a .
.
Consider a system in which the i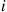 th component functions for a random length of time having distribution Fi
th component functions for a random length of time having distribution Fi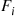 and then fails. Once failed it remains in that state forever. Assuming that the individual component lifetimes are independent, how can we express the distribution of system lifetime as a function of the system reliability function r(p)
and then fails. Once failed it remains in that state forever. Assuming that the individual component lifetimes are independent, how can we express the distribution of system lifetime as a function of the system reliability function r(p)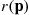 and the individual component lifetime distributions Fi,i=1,…,n
and the individual component lifetime distributions Fi,i=1,…,n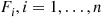 ?
?
To answer this we first note that the system will function for a length of time t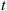 or greater if and only if it is still functioning at time t
or greater if and only if it is still functioning at time t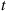 . That is, letting F
. That is, letting F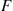 denote the distribution of system lifetime, we have
denote the distribution of system lifetime, we have
F¯(t)=P{systemlife>t}=P{system is functioning at timet}
But, by the definition of r(p)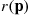 we have
we have
P{system is functioning at timet}=r(P1(t),…,Pn(t))
where
Pi(t)=P{componentiis functioning att}=P{lifetimeofi>t}=F¯i(t)
Hence, we see that
F¯(t)=r(F¯1(t),…,F¯n(t)) (9.14)
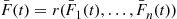 (9.14)
(9.14)
Example 9.20
In a series system, r(p)=∏1npi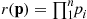 and so from Equation (9.14)
and so from Equation (9.14)
F¯(t)=∏1nF¯i(t)
which is, of course, quite obvious since for a series system the system life is equal to the minimum of the component lives and so will be greater than t if and only if all component lives are greater than t
if and only if all component lives are greater than t . ■
. ■
Example 9.21
In a parallel system r(p)=1-∏1n(1-pi)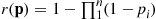 and so
and so
F¯(t)=1-∏1nFi(t)
The preceding is also easily derived by noting that, in the case of a parallel system, the system life is equal to the maximum of the component lives. ■
For a continuous distribution G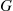 , we define λ(t)
, we define λ(t)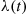 , the failure rate function of G
, the failure rate function of G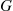 , by
, by
λ(t)=g(t)G¯(t)
where g(t)=d/dtG(t)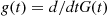 . In Section 5.2.2, it is shown that if G
. In Section 5.2.2, it is shown that if G is the distribution of the lifetime of an item, then λ(t)
is the distribution of the lifetime of an item, then λ(t)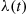 represents the probability intensity that a t
represents the probability intensity that a t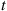 -year-old item will fail. We say that G
-year-old item will fail. We say that G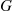 is an increasing failure rate (IFR) distribution if λ(t)
is an increasing failure rate (IFR) distribution if λ(t)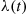 is an increasing function of t
is an increasing function of t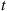 . Similarly, we say that G
. Similarly, we say that G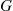 is a decreasing failure rate (DFR) distribution if λ(t)
is a decreasing failure rate (DFR) distribution if λ(t)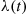 is a decreasing function of t
is a decreasing function of t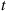 .
.
Example 9.22
The Weibull Distribution
A random variable is said to have the Weibull distribution if its distribution is given, for some λ>0,α>0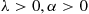 , by
, by
G(t)=1-e-(λt)α,t⩾0
The failure rate function for a Weibull distribution equals
λ(t)=e-(λt)αα(λt)α-1λe-(λt)α=αλ(λt)α-1
Thus, the Weibull distribution is IFR when α⩾1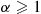 , and DFR when 0<α⩽1
, and DFR when 0<α⩽1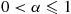 ; when α=1,G(t)=1-e-λt
; when α=1,G(t)=1-e-λt , the exponential distribution, which is both IFR and DFR. ■
, the exponential distribution, which is both IFR and DFR. ■
Example 9.23
The Gamma Distribution
A random variable is said to have a gamma distribution if its density is given, for some λ>0,α>0 , by
, by
g(t)=λe-λt(λt)α-1Γ(α)fort⩾0
where
Γ(α)≡∫0∞e-ttα-1dt
For the gamma distribution,
1λ(t)=G¯(t)g(t)=∫t∞λe-λx(λx)α-1dxλe-λt(λt)α-1=∫t∞e-λ(x-t)xtα-1dx
With the change of variables u=x-t , we obtain
, we obtain
1λ(t)=∫0∞e-λu1+utα-1du
Hence, G is IFR when α⩾1
is IFR when α⩾1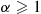 and is DFR when 0<α⩽1
and is DFR when 0<α⩽1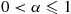 . ■
. ■
Suppose that the lifetime distribution of each component in a monotone system is IFR. Does this imply that the system lifetime is also IFR? To answer this, let us at first suppose that each component has the same lifetime distribution, which we denote by G . That is, Fi(t)=G(t),i=1,…,n
. That is, Fi(t)=G(t),i=1,…,n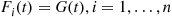 . To determine whether the system lifetime is IFR, we must compute λF(t)
. To determine whether the system lifetime is IFR, we must compute λF(t)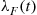 , the failure rate function of F
, the failure rate function of F . Now, by definition,
. Now, by definition,
λF(t)=(d/dt)F(t)F¯(t)=(d/dt)[1-r(G¯(t))]r(G¯(t))
where
r(G¯(t))≡r(G¯(t),…,G¯(t))
Hence,
λF(t)=r′(G¯(t))r(G¯(t))G′(t)=G¯(t)r′(G¯(t))r(G¯(t))G′(t)G¯(t)=λG(t)pr′(p)r(p)p=G¯(t) (9.15)
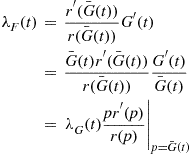 (9.15)
(9.15)
Since G¯(t) is a decreasing function of t
is a decreasing function of t , it follows from Equation (9.15) that if each component of a coherent system has the same IFR lifetime distribution, then the distribution of system lifetime will be IFR if pr′(p)/r(p)
, it follows from Equation (9.15) that if each component of a coherent system has the same IFR lifetime distribution, then the distribution of system lifetime will be IFR if pr′(p)/r(p)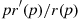 is a decreasing function of p
is a decreasing function of p 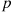 .
.
Example 9.24
The k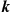 -out-of-n
-out-of-n System with Identical Components
System with Identical Components
Consider the k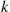 -out-of-n
-out-of-n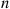 system, which will function if and only if k
system, which will function if and only if k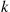 or more components function. When each component has the same probability p
or more components function. When each component has the same probability p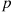 of functioning, the number of functioning components will have a binomial distribution with parameters n
of functioning, the number of functioning components will have a binomial distribution with parameters n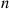 and p
and p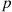 . Hence,
. Hence,
r(p)=∑i=knnipi(1-p)n-i
which, by continual integration by parts, can be shown to be equal to
r(p)=n!(k-1)!(n-k)!∫0pxk-1(1-x)n-kdx
Upon differentiation, we obtain
r′(p)=n!(k-1)!(n-k)!pk-1(1-p)n-k
Therefore,
pr′(p)r(p)=r(p)pr′(p)-1=1p∫0pxpk-11-x1-pn-kdx-1
Letting y=x/p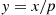 yields
yields
pr′(p)r(p)=∫01yk-11-yp1-pn-kdy-1
Since (1-yp)/(1-p)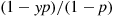 is increasing in p
is increasing in p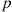 , it follows that pr′(p)/r(p)
, it follows that pr′(p)/r(p)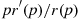 is decreasing in p
is decreasing in p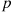 . Thus, if a k
. Thus, if a k -out-of-n
-out-of-n system is composed of independent, like components having an increasing failure rate, the system itself has an increasing failure rate. ■
system is composed of independent, like components having an increasing failure rate, the system itself has an increasing failure rate. ■
It turns out, however, that for a k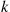 -out-of-n
-out-of-n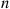 system, in which the independent components have different IFR lifetime distributions, the system lifetime need not be IFR. Consider the following example of a two-out-of-two (that is, a parallel) system.
system, in which the independent components have different IFR lifetime distributions, the system lifetime need not be IFR. Consider the following example of a two-out-of-two (that is, a parallel) system.
Example 9.25
A Parallel System That Is Not IFR
The life distribution of a parallel system of two independent components, the i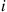 th component having an exponential distribution with mean 1/i,i=1,2
th component having an exponential distribution with mean 1/i,i=1,2 , is given by
, is given by
F¯(t)=1-(1-e-t)(1-e-2t)=e-2t+e-t-e-3t
Therefore,
λ(t)=f(t)F¯(t)=2e-2t+e-t-3e-3te-2t+e-t-e-3t
It easily follows upon differentiation that the sign of λ′(t)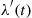 is determined by e-5t-e-3t+3e-4t
is determined by e-5t-e-3t+3e-4t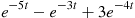 , which is positive for small values and negative for large values of t
, which is positive for small values and negative for large values of t . Therefore, λ(t)
. Therefore, λ(t) is initially strictly increasing, and then strictly decreasing. Hence, F
is initially strictly increasing, and then strictly decreasing. Hence, F is not IFR. ■
is not IFR. ■
Remark
The result of the preceding example is quite surprising at first glance. To obtain a better feel for it we need the concept of a mixture of distribution functions. The distribution function G is said to be a mixture of the distributions G1
is said to be a mixture of the distributions G1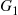 and G2
and G2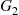 if for some p,0<p<1
if for some p,0<p<1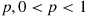 ,
,
G(x)=pG1(x)+(1-p)G2(x) (9.16)
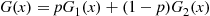 (9.16)
(9.16)
Mixtures occur when we sample from a population made up of two distinct groups. For example, suppose we have a stockpile of items of which the fraction p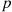 are type 1 and the fraction 1-p
are type 1 and the fraction 1-p are type 2. Suppose that the lifetime distribution of type 1 items is G1
are type 2. Suppose that the lifetime distribution of type 1 items is G1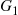 and of type 2 items is G2
and of type 2 items is G2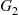 . If we choose an item at random from the stockpile, then its life distribution is as given by Equation (9.16).
. If we choose an item at random from the stockpile, then its life distribution is as given by Equation (9.16).
Consider now a mixture of two exponential distributions having rates λ1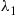 and λ2
and λ2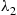 where λ1<λ2
where λ1<λ2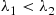 . We are interested in determining whether or not this mixture distribution is IFR. To do so, we note that if the item selected has survived up to time t
. We are interested in determining whether or not this mixture distribution is IFR. To do so, we note that if the item selected has survived up to time t , then its distribution of remaining life is still a mixture of the two exponential distributions. This is so since its remaining life will still be exponential with rate λ1
, then its distribution of remaining life is still a mixture of the two exponential distributions. This is so since its remaining life will still be exponential with rate λ1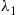 if it is type 1 or with rate λ2
if it is type 1 or with rate λ2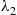 if it is a type 2 item. However, the probability that it is a type 1 item is no longer the (prior) probability p
if it is a type 2 item. However, the probability that it is a type 1 item is no longer the (prior) probability p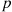 but is now a conditional probability given that it has survived to time t
but is now a conditional probability given that it has survived to time t . In fact, its probability of being a type 1 is
. In fact, its probability of being a type 1 is
P{type 1∣life>t}=P{type1,life>t}P{life>t}=pe-λ1tpe-λ1t+(1-p)e-λ2t
As the preceding is increasing in t , it follows that the larger t
, it follows that the larger t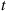 is, the more likely it is that the item in use is a type 1 (the better one, since λ1<λ2
is, the more likely it is that the item in use is a type 1 (the better one, since λ1<λ2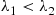 ). Hence, the older the item is, the less likely it is to fail, and thus the mixture of exponentials far from being IFR is, in fact, DFR.
). Hence, the older the item is, the less likely it is to fail, and thus the mixture of exponentials far from being IFR is, in fact, DFR.
Now, let us return to the parallel system of two exponential components having respective rates λ1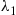 and λ2
and λ2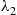 . The lifetime of such a system can be expressed as the sum of two independent random variables, namely,
. The lifetime of such a system can be expressed as the sum of two independent random variables, namely,
systemlife=Exp(λ1+λ2)+Exp(λ1)withprobabilityλ2λ1+λ2Exp(λ2)withprobabilityλ1λ1+λ2
The first random variable whose distribution is exponential with rate λ1+λ2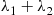 represents the time until one of the components fails, and the second, which is a mixture of exponentials, is the additional time until the other component fails. (Why are these two random variables independent?)
represents the time until one of the components fails, and the second, which is a mixture of exponentials, is the additional time until the other component fails. (Why are these two random variables independent?)
Now, given that the system has survived a time t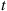 , it is very unlikely when t
, it is very unlikely when t is large that both components are still functioning, but instead it is far more likely that one of the components has failed. Hence, for large t
is large that both components are still functioning, but instead it is far more likely that one of the components has failed. Hence, for large t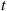 , the distribution of remaining life is basically a mixture of two exponentials—and so as t
, the distribution of remaining life is basically a mixture of two exponentials—and so as t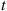 becomes even larger its failure rate should decrease (as indeed occurs). ■
becomes even larger its failure rate should decrease (as indeed occurs). ■
Recall that the failure rate function of a distribution F(t)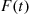 having density f(t)=F′(t)
having density f(t)=F′(t)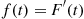 is defined by
is defined by
λ(t)=f(t)1-F(t)
By integrating both sides, we obtain
∫0tλ(s)ds=∫0tf(s)1-F(s)ds=-logF¯(t)
Hence,
F¯(t)=e-Λ(t) (9.17)
 (9.17)
(9.17)
where
Λ(t)=∫0tλ(s)ds
The function Λ(t)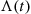 is called the hazard function of the distribution F
is called the hazard function of the distribution F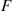 .
.
Definition 9.1
A distribution F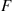 is said to have increasing failure on the average (IFRA) if
is said to have increasing failure on the average (IFRA) if
Λ(t)t=∫0tλ(s)dst (9.18)
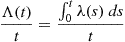 (9.18)
(9.18)
increases in t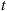 for t⩾0
for t⩾0 .
.
In other words, Equation (9.18) states that the average failure rate up to time t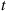 increases as t
increases as t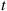 increases. It is not difficult to show that if F
increases. It is not difficult to show that if F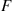 is IFR, then F
is IFR, then F is IFRA; but the reverse need not be true.
is IFRA; but the reverse need not be true.
Note that F is IFRA if Λ(s)/s⩽Λ(t)/t
is IFRA if Λ(s)/s⩽Λ(t)/t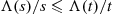 whenever 0⩽s⩽t
whenever 0⩽s⩽t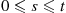 , which is equivalent to
, which is equivalent to
Λ(αt)αt⩽Λ(t)tfor0⩽α⩽1,allt⩾0
But by Equation (9.17) we see that Λ(t)=-logF¯(t)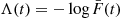 , and so the preceding is equivalent to
, and so the preceding is equivalent to
-logF¯(αt)⩽-αlogF¯(t)
or equivalently,
logF¯(αt)⩾logF¯α(t)
which, since log x is a monotone function of x
is a monotone function of x , shows that F
, shows that F is IFRA if and only if
is IFRA if and only if
F¯(αt)⩾F¯α(t)for0⩽α⩽1,allt⩾0 (9.19)
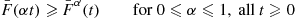 (9.19)
(9.19)
For a vector p=(p1,…,pn)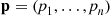 we define pα=(p1α,…,pnα)
we define pα=(p1α,…,pnα) . We shall need the following proposition.
. We shall need the following proposition.
Proposition 9.2
Any reliability function r(p)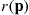 satisfies
satisfies
r(pα)⩾[r(p)]α,0⩽α⩽1
Proof
We prove this by induction on n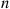 , the number of components in the system. If n=1
, the number of components in the system. If n=1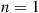 , then either r(p)≡0,r(p)≡1,orr(p)≡p
, then either r(p)≡0,r(p)≡1,orr(p)≡p . Hence, the proposition follows in this case.
. Hence, the proposition follows in this case.
Assume that Proposition 9.2 is valid for all monotone systems of n-1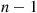 components and consider a system of n
components and consider a system of n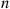 components having structure function ϕ
components having structure function ϕ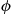 . By conditioning upon whether or not the n
. By conditioning upon whether or not the n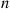 th component is functioning, we obtain
th component is functioning, we obtain
r(pα)=pnαr(1n,pα)+(1-pnα)r(0n,pα) (9.20)
 (9.20)
(9.20)
Now consider a system of components 1 through n-1 having a structure function ϕ1(x)=ϕ(1n,x)
having a structure function ϕ1(x)=ϕ(1n,x)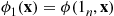 . The reliability function for this system is given by r1(p)=r(1n,p)
. The reliability function for this system is given by r1(p)=r(1n,p)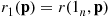 ; hence, from the induction assumption (valid for all monotone systems of n-1
; hence, from the induction assumption (valid for all monotone systems of n-1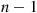 components), we have
components), we have
r(1n,pα)⩾[r(1n,p)]α
Similarly, by considering the system of components 1 through n-1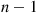 and structure function ϕ0(x)=ϕ(0n,x)
and structure function ϕ0(x)=ϕ(0n,x)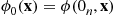 , we obtain
, we obtain
r(0n,pα)⩾[r(0n,p)]α
Thus, from Equation (9.20), we obtain
r(pα)⩾pnα[r(1n,p)]α+(1-pnα)[r(0n,p)]α
which, by using the lemma to follow (with λ=pn,x=r(1n,p)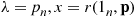 , y=r(0n,p)
, y=r(0n,p)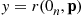 ), implies that
), implies that
r(pα)⩾[pnr(1n,p)+(1-pn)r(0n,p)]α=[r(p)]α
which proves the result. ■
Lemma 9.3
If 0⩽α⩽1,0⩽λ⩽1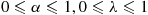 , then
, then
h(y)=λαxα+(1-λα)yα-(λx+(1-λ)y)α⩾0
for all 0⩽y⩽x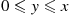 .
.
Proof
The proof is left as an exercise. ■
We are now ready to prove the following important theorem.
Theorem 9.2
For a monotone system of independent components, if each component has an IFRA lifetime distribution, then the distribution of system lifetime is itself IFRA.
Proof
The distribution of system lifetime F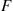 is given by
is given by
F¯(αt)=r(F¯1(αt),…,F¯n(αt))
Hence, since r is a monotone function, and since each of the component distributions F¯i
is a monotone function, and since each of the component distributions F¯i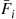 is IFRA, we obtain from Equation (9.19)
is IFRA, we obtain from Equation (9.19)
F¯(αt)⩾r(F¯1α(t),…,F¯nα(t))⩾[r(F¯1(t),…,F¯n(t))]α=F¯α(t)
which by Equation (9.19) proves the theorem. The last inequality followed, of course, from Proposition 9.2. ■
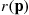 is based on expressing the desired probability as the probability of the intersection of events. To do so, let
is based on expressing the desired probability as the probability of the intersection of events. To do so, let 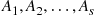 denote the minimal path sets as before, and define the events,
denote the minimal path sets as before, and define the events, 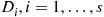 by
by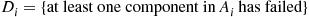
 (9.11)
(9.11)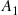 is down can only increase the probability that at least one component of
is down can only increase the probability that at least one component of 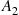 is down (or else leave the probability unchanged if
is down (or else leave the probability unchanged if 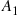 and
and 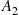 do not overlap). Hence, intuitively
do not overlap). Hence, intuitively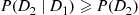
 (9.12)
(9.12)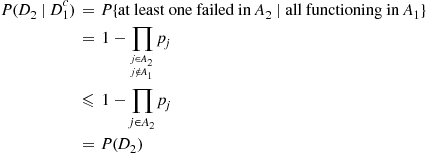
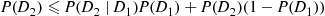
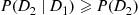

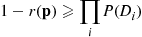
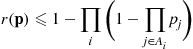
 denote the minimal cut sets and define the events
denote the minimal cut sets and define the events  by
by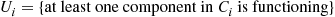
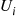 occur, we have
occur, we have
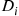 . Hence,
. Hence,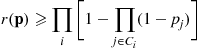
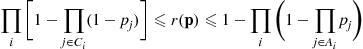 (9.13)
(9.13)
 if there is not too much overlap in the minimal path sets, and the lower bound to be close if there is not too much overlap in the minimal cut sets.
if there is not too much overlap in the minimal path sets, and the lower bound to be close if there is not too much overlap in the minimal cut sets. , we define
, we define  to be the probability that the random variable is greater than
to be the probability that the random variable is greater than  .
.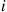 th component functions for a random length of time having distribution
th component functions for a random length of time having distribution 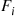 and then fails. Once failed it remains in that state forever. Assuming that the individual component lifetimes are independent, how can we express the distribution of system lifetime as a function of the system reliability function
and then fails. Once failed it remains in that state forever. Assuming that the individual component lifetimes are independent, how can we express the distribution of system lifetime as a function of the system reliability function 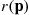 and the individual component lifetime distributions
and the individual component lifetime distributions 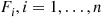 ?
?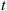 or greater if and only if it is still functioning at time
or greater if and only if it is still functioning at time 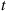 . That is, letting
. That is, letting 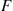 denote the distribution of system lifetime, we have
denote the distribution of system lifetime, we have
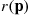 we have
we have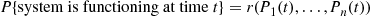
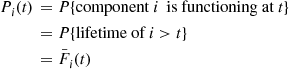
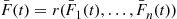 (9.14)
(9.14)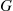 , we define
, we define 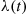 , the failure rate function of
, the failure rate function of 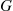 , by
, by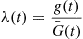
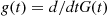 . In Section 5.2.2, it is shown that if
. In Section 5.2.2, it is shown that if  is the distribution of the lifetime of an item, then
is the distribution of the lifetime of an item, then 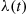 represents the probability intensity that a
represents the probability intensity that a 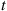 -year-old item will fail. We say that
-year-old item will fail. We say that 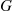 is an increasing failure rate (IFR) distribution if
is an increasing failure rate (IFR) distribution if 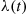 is an increasing function of
is an increasing function of 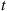 . Similarly, we say that
. Similarly, we say that 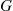 is a decreasing failure rate (DFR) distribution if
is a decreasing failure rate (DFR) distribution if 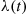 is a decreasing function of
is a decreasing function of 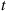 .
. . That is,
. That is, 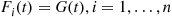 . To determine whether the system lifetime is IFR, we must compute
. To determine whether the system lifetime is IFR, we must compute 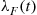 , the failure rate function of
, the failure rate function of 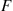 . Now, by definition,
. Now, by definition,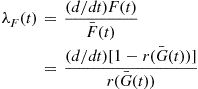
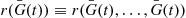
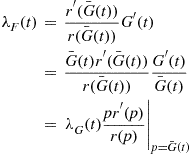 (9.15)
(9.15)
 is a decreasing function of
is a decreasing function of  , it follows from Equation (9.15) that if each component of a coherent system has the same IFR lifetime distribution, then the distribution of system lifetime will be IFR if
, it follows from Equation (9.15) that if each component of a coherent system has the same IFR lifetime distribution, then the distribution of system lifetime will be IFR if 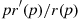 is a decreasing function of
is a decreasing function of 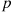 .
.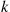 -out-of-
-out-of-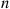 system, in which the independent components have different IFR lifetime distributions, the system lifetime need not be IFR. Consider the following example of a two-out-of-two (that is, a parallel) system.
system, in which the independent components have different IFR lifetime distributions, the system lifetime need not be IFR. Consider the following example of a two-out-of-two (that is, a parallel) system.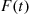 having density
having density 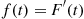 is defined by
is defined by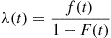

 (9.17)
(9.17)
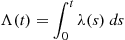
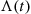 is called the hazard function of the distribution
is called the hazard function of the distribution 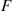 .
.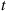 increases as
increases as 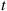 increases. It is not difficult to show that if
increases. It is not difficult to show that if 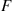 is IFR, then
is IFR, then  is IFRA; but the reverse need not be true.
is IFRA; but the reverse need not be true. is IFRA if
is IFRA if 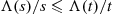 whenever
whenever 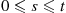 , which is equivalent to
, which is equivalent to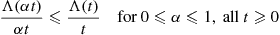
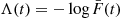 , and so the preceding is equivalent to
, and so the preceding is equivalent to
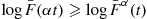
 is a monotone function of
is a monotone function of  , shows that
, shows that  is IFRA if and only if
is IFRA if and only if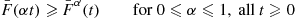 (9.19)
(9.19)
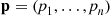 we define
we define  . We shall need the following proposition.
. We shall need the following proposition. and the component lifetime distributions
and the component lifetime distributions  .
.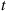 or larger if and only if the system is still functioning at time
or larger if and only if the system is still functioning at time 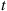 , we have
, we have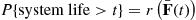
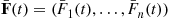 . Hence, by a well-known formula that states that for any nonnegative random variable
. Hence, by a well-known formula that states that for any nonnegative random variable  ,
,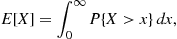
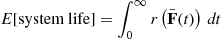 (9.21)
(9.21)