TRY THIS: For more practice, try this! Take two clean, empty egg cartons, and have a grown-up cut off 2 sections from each so they look like “tins” with 10 sections each.

Then use coins or other small objects to practice these kinds of problems. Or make up your own problems!

Upstairs and Downstairs: Adding and Subtracting 10 (and Groups of 10)

Whenever we add 10, all we’re doing is adding a tin, right? For example, if we had 53 + 10, we could imagine that we start with 5 tins and 3 extra buns. To add 10, that’s just adding 1 tin, which changes the 5 to a 6, and we get a total of 63!

We already know from Chapter 5 that we could model the problem like this:

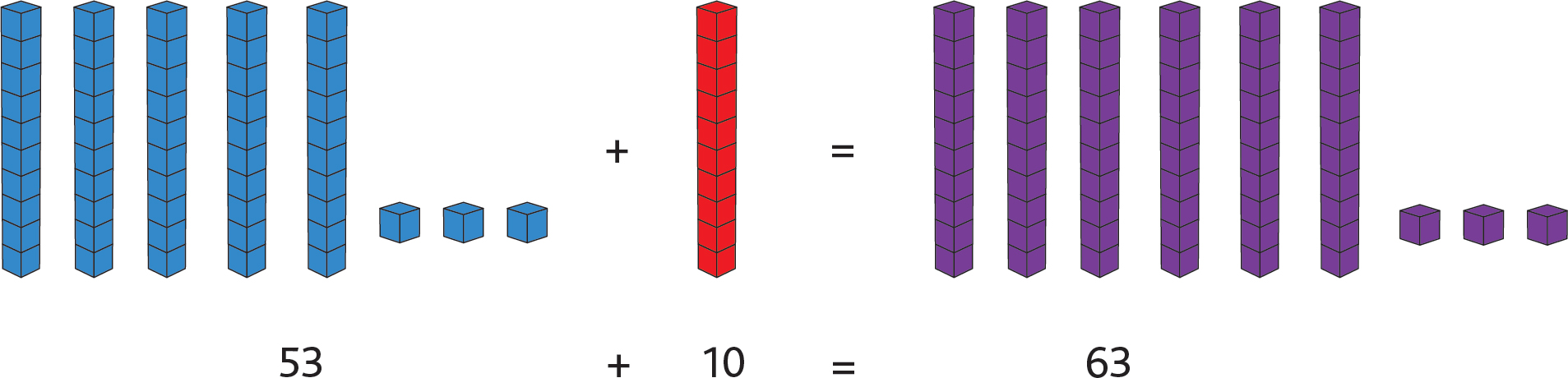
And notice that adding 1 ten means we just make the tens digit bigger by 1!

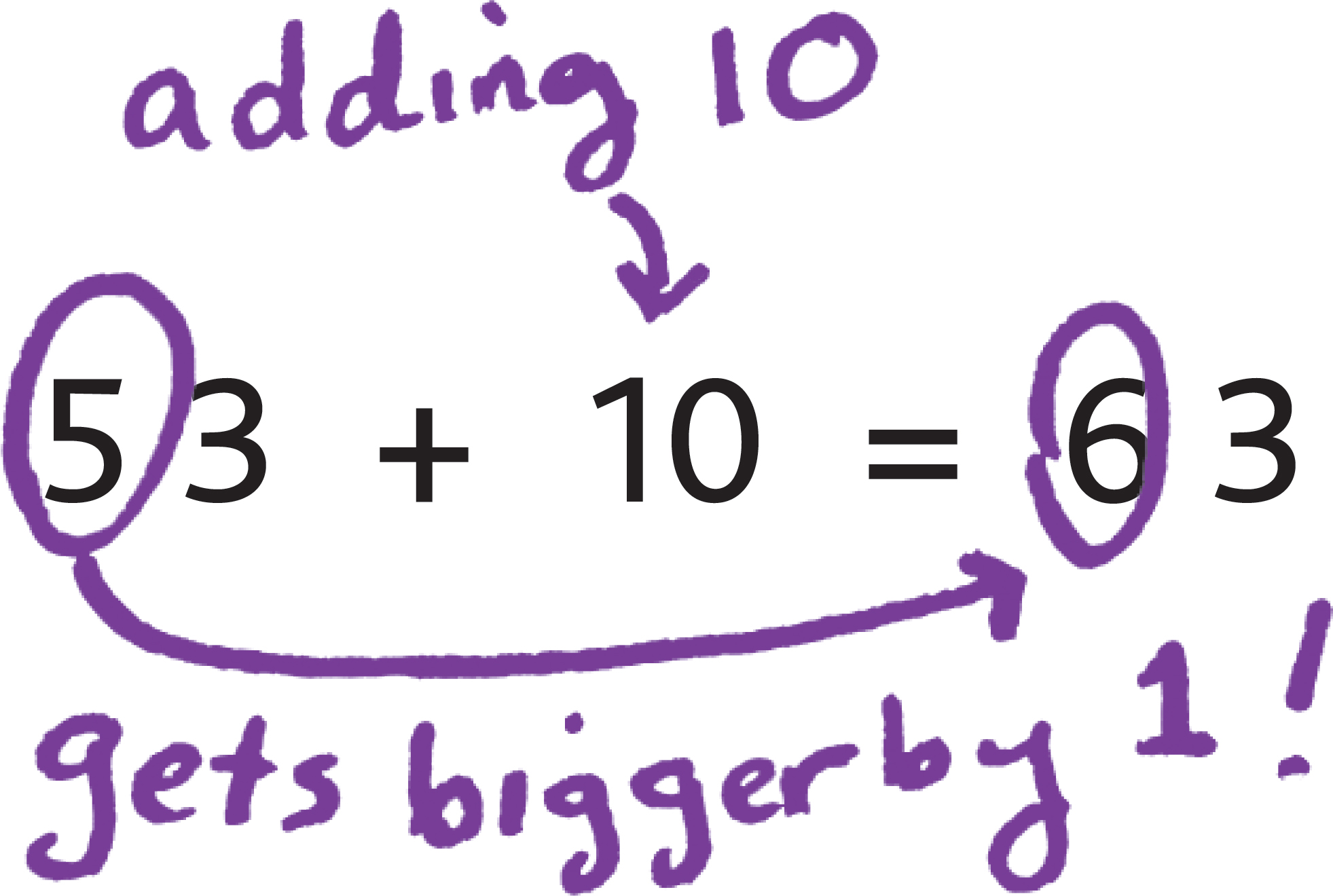
And subtracting 10 is just as easy!

Subtracting 10 is a lot like adding 10—but in order to subtract 10, we make the tens digit smaller by 1! Let’s do 53 – 10, and look, we get 43!

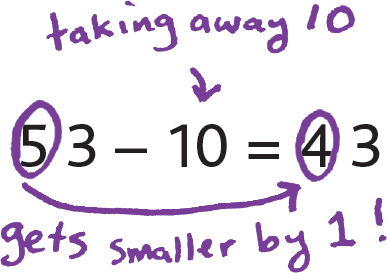
We can also look at this hundred chart—adding 10 means we go directly “downstairs” on the chart, and subtracting 10 means we go directly “upstairs.” Like if we want to add 35 + 10, we look at the 35 and go downstairs to see that 35 + 10 = 45. Or to subtract 35 – 10, we’d go upstairs to see that 35 – 10 = 25.

Not so bad, right?