SHORTCUT ALERT! Easy Tricks for Learning Some of the Facts
figure

LOOK FOR DOUBLES!

Let’s say we know our doubles facts from page 41, like 7 + 7 = 14, and we get a problem like 7 + 8. We might think, “Hey, this is 1 more than 7 + 7, so the answer must be 15!” Look out for addition problems that are near doubles facts that you already know. Your answer might be easier to get than you thought!

FINDING 10s

Sometimes we’ll be asked to add three numbers together, like 3 + 6 + 7 = ? Sure, we could add 3 + 6 first (to get 9), and then add 9 + 7. Or we could look to see if any pairs of numbers add up to 10, and—yep!—since 3 + 7 = 10, and the order of addition doesn’t change the answer, we can add 3 + 7 (to get 10) first.

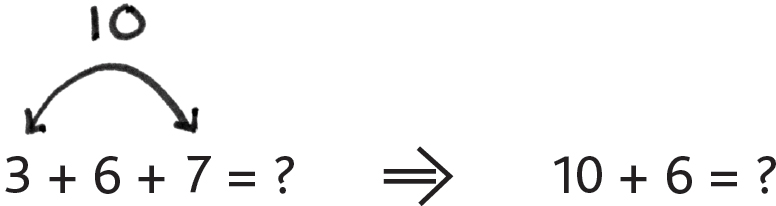
figure

Then we can easily add 10 + 6 to get our answer, 16!

We’re about to tackle some bigger numbers, so this is a great time to put on our thinking caps!

More Give and Take…with Bigger Numbers!

Let’s do 53 + 38. Hmm, nobody is near 10, but 38 sure is near 40! In order to make 38 become 40, we need to give 2 to it, which means we need to take 2 from 53, and it becomes 51.

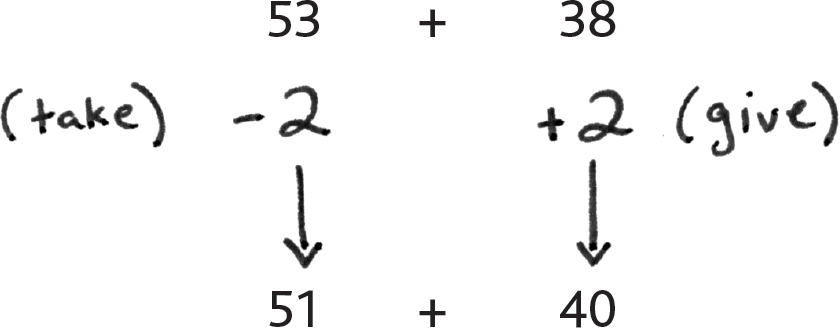
figure

So we’ve turned 53 + 38 into 51 + 40! And that’s a much easier problem because we’re just adding 4 tens to the 5 tens in 51, and that means we have a total of 9 tens with 1 extra one: 51 + 40 = 91. Yep, we just showed that 53 + 38 = 91. How about that!

By the way, with bigger numbers, it’s ALWAYS a great idea to write out the “Give and Take” strategy. It’s not like we’re drawing pictures of muffin tins that would take forever; we’re just showing our work, and that’s a very good thing!

figure

You might have noticed that there is more than one way to “Give and Take,” depending on which number you want to end in 0. But make sure that whatever amount you take from one number is the same amount you give to the other number! For example, to add 41 + 28, we can’t make them both end in 0, as tempting as it looks to try! Check it out:

figure

So both 40 + 29 and 39 + 30 give the right answer, which is 69! Remember, we’re not changing the total number of toys here—that would change the answer! We’re just moving the numbers around to make the addition look nicer and be easier to solve.

figure

Isn’t it nice, turning these addition problems into easier ones? So far, we’ve seen two ways of doing that. Trick #1 is to imagine our tins and buns, moving stuff around so we fill up a tin. Trick #2 is the “Give and Take” method we just saw. Now I’ll show you Trick #3—where we do an easier problem first, and then fix the answer later! These are all great options for doing math in our heads—and it’s up to you to decide which method you want to use. Let’s do it!

Easy Addition Trick #3: Clean the Mess Later!

Have you ever been playing with your toys and then you want to go do something fun…but you really don’t want to clean up the mess yet?

Yep, all the time. Wait! You’re not going to tell on me, are you?

You might think, “Oh, I’ll do what I want now, and then I’ll just clean up these messy toys later.” Depending on how strict your parents are, that might or might not work very well for you! But we can do this with math—sort of.

Let’s add 32 + 49. We could say to ourselves, “Gosh, 32 + 49 is messy. Instead, I’m going to do an easier version. I’m going to take away 2 from the 32 and do the easier problem 30 + 49, which is just 79. But that’s not our final answer. We made a mess when we took away 2, and now we have to clean it up by adding 2 back in to get our real answer: 79 + 2 = 81. Done!”

See how that works? There are so many ways to think about addition. Use whichever ways you like most. The point is to move around the numbers and turn the problem into an easier one—usually a problem that uses a number ending in 0.