4
EXUBERANT: THE DELIGHT OF DENDRITIC GROWTH

The fractal branching patterns made by growing sodium silicate crystals

Snowflake-like dendritic growth of silver crystals in a displacement reaction of silver nitrate and copper
Among these myriads of enchanting little stars, in their hidden splendor that was too small for man's naked eye to see, there was not one like unto another; an endless inventiveness governed the development and unthinkable differentiation of one and the same basic scheme, the equilateral, equiangled hexagon. Yet each, in itself . . . was absolutely symmetrical, icily regular in form.
This is Hans Castorp, the self-absorbed hero of Thomas Mann's 1924 novel The Magic Mountain, meditating on the shape of snowflakes while succumbing to exhausted sleep on a skiing outing. It could sound as though Castorp is entranced by the snowflake's beauty, but in fact it unnerved him. “They were too regular,” he says, “as substance adapted to life never was to this degree—the living principle shuddered at this perfect precision, found it deathly, the very marrow of death.” He decides that this must be why the builders in ancient times introduced slight deviations from absolute symmetry in their buildings: to imbue them with a sense of vitality.
What's truly unsettling about snowflakes is perhaps also what is beautiful about them: not so much their geometric symmetry, but the fact that these little flakes of ice seem poised on the verge of bursting free of it. Ordinary crystals have a blocky tidiness, as we saw in chapter 2. But in the Christmas tree arms of snowflakes, geometry runs riot, ramified into exuberant branches piled upon branches as if this were a thing with a life of its own. To Chinese scholars of the first-century Han dynasty, these tiny ice crystals were indeed plantlike “flowers of snow.” Just a little more of this quasi-organic abandon and the orderliness would be lost altogether. It's probably this feature that struck Castorp as “uncanny.”
Scientists through the ages have pondered the problem of the snowflake. You just couldn't ignore so astonishing a natural phenomenon, especially after the invention of the microscope in the seventeenth century brought these delicate creations into sharper focus. What could possibly be the cause of this “endless inventiveness”? What need did nature have for it?
Johannes Kepler, the German astronomer and mathematician whom we encountered earlier trying to explain the shapes of crystals, thought long and hard about snowflakes. They were, in fact, the motivation for those impressive intuitions about crystallinity. While working in the court of the Holy Roman Emperor Rudolf II in Prague, in the winter of 1610 Kepler wrote a little book called De nive hexangula (On the six-cornered snowflake) as a New Year's gift for a noble patron. Here he set himself the task of explaining the snowflake. “What is the origin of the number six?,” he asked:
Who carved the nucleus, before it fell, into six horns of ice? What cause is it that prescribes in that surface, which is now in the very act of condensing, six points in a circle for six prongs to be welded on to them?

Dendritic silver crystals grown by electrochemical reduction of a silver salt

Tin crystals grown in a displacement reaction of tin chloride and zinc


Dendritic silver crystals, seen in transmitted light, formed in a displacement reaction of silver nitrate and copper

Dendritic silver crystals, seen in transmitted light, formed in a displacement reaction of silver nitrate and copper
“What's unsettling about snowflakes is not so much their geometric symmetry, but the fact that they seem poised on the verge of bursting free of it.”
We saw how he decided that the hexagonal symmetry might be explained by the packing of “globules of water.” But try as he might, he couldn't account for the snowflake's branches. In the end, apparently a little desperate, he could only invoke that mystical notion of a “formative faculty” at work that is part of God's design. “Formative reason does not act only for a purpose, but also to adorn,” Kepler wrote, adding rather delightfully that “it is in the habit of playing with the passing moment.”
As you might imagine, this didn't seem much of an explanation to scientists in the following ages. In the mid-nineteenth century, the eminent biologist Thomas Henry Huxley made it clear that no one any longer tried to invoke some mysterious “faculty” or “spirit” that “guided the aqueous particles to their places in the facets of the crystal, or among the leaflets of the hoar-frost.” No: it had to be the principles of physics and chemistry alone that generated these wondrous objects.
But how? Until the middle of the twentieth century, all scientists could do was to describe and document. The Vermont farmer Wilson Bentley took thousands of photographs of snowflakes between 1885 and 1931; in the latter year he published a book of his stunning images called Snow Crystals in collaboration with meteorological physicist William Humphreys. As a catalogue of the wonders produced by the laws of chemistry, it is surely a forerunner to this book, and it inspired many scientists to ponder the laws that might govern “flowers of snow.” That botanical analogy echoes the description of snowflakes given by Scottish zoologist D’Arcy Wentworth Thompson in his magnum opus on pattern and form in nature, On Growth and Form (1917):
The beauty of a snow-crystal depends on its mathematical regularity and symmetry, but some-how the association of many variants of a single type, all related but no two the same, vastly increases our pleasure and admiration. Such is the peculiar beauty which a Japanese artist sees in a bed of rushes or a clump of bamboos, especially when the wind's ablowing: and such is the phase-beauty of a flowering spray when it shews every gradation from opening bud to fading flower.
The puzzle here is not just about snowflakes. They are simply the most familiar example of a common pattern that may appear as crystals grow. The real signature of the snowflake is not, as Kepler and others before and after him supposed, their sixfold (hexagonal) symmetry, but the individual arms: typically, needle-like tips decorated with the fernlike iterations of branches. Metallurgists have long known that these structures may appear too in molten metals as they cool and solidify. Their formation is known as dendritic growth, from the Greek word for “branch.” Branching dendritic growth can also develop in the chemical process called electrodeposition, in which a metal dissolved in the form of ions in solution gets deposited on an electrode immersed in the solution, as an electrical current passes through it (see chapter 6).



If we're to explain dendritic growth, there are two questions to answer. First, why the needles? Why, as a molten metal freezes, doesn't the boundary separating the liquid from the solid advance smoothly, like a wave on the ocean? What makes one part of it outrun the rest and surge forth into a fingerlike tip? And second, what makes this tip itself sprout side branches—which, moreover, seem often to arrange themselves geometrically, branching out at a particular angle?
The answers emerged in fits and starts between the 1940s and 1970s. The tips and branches of dendritic growth are examples of a so-called growth instability. To put it simply, this means that a process of steady growth gives way to something less smooth and regular.
Growth instabilities happen all around us. One such process causes regular ranks of sand ripples and dunes to rise up from a desert surface as sand grains blow randomly across it, one part of the surface accumulating grains faster than others. Another instability makes the layer of dew condensing onto the strands of a spider's web at dawn retract into a series of little droplets, like pearls on a string.

The fundamental growth instability of dendritic growth was identified in 1963 by two American scientists, William Mullins and Robert Sekerka. They pointed out that the tiniest wiggle appearing by chance on the surface of a solidifying metal, as it grows in the cooling molten mass, will get amplified and quickly surge forward into a fingerlike protrusion that gets narrower as it grows. That's because a protrusion like this can shed its heat faster than the rest of the solid, and so it freezes more quickly. It's a process of positive feedback: the further the finger sticks out, the faster it grows.
Mullins and Sekerka realized that this process of finger formation should keep recurring: it will happen on the sides of the needle tip too, creating side branches—and they in turn will also branch. Before you know it, you have a profusion of branches. There's a limit to how small they can get, though, because surface tension at the boundary has the opposing effect of pulling the surface flat, as it does for the surface of water in a glass.
“The tiniest wiggle appearing by chance on the surface will get amplified and quickly surge forward into a fingerlike protrusion that gets narrower as it grows.”


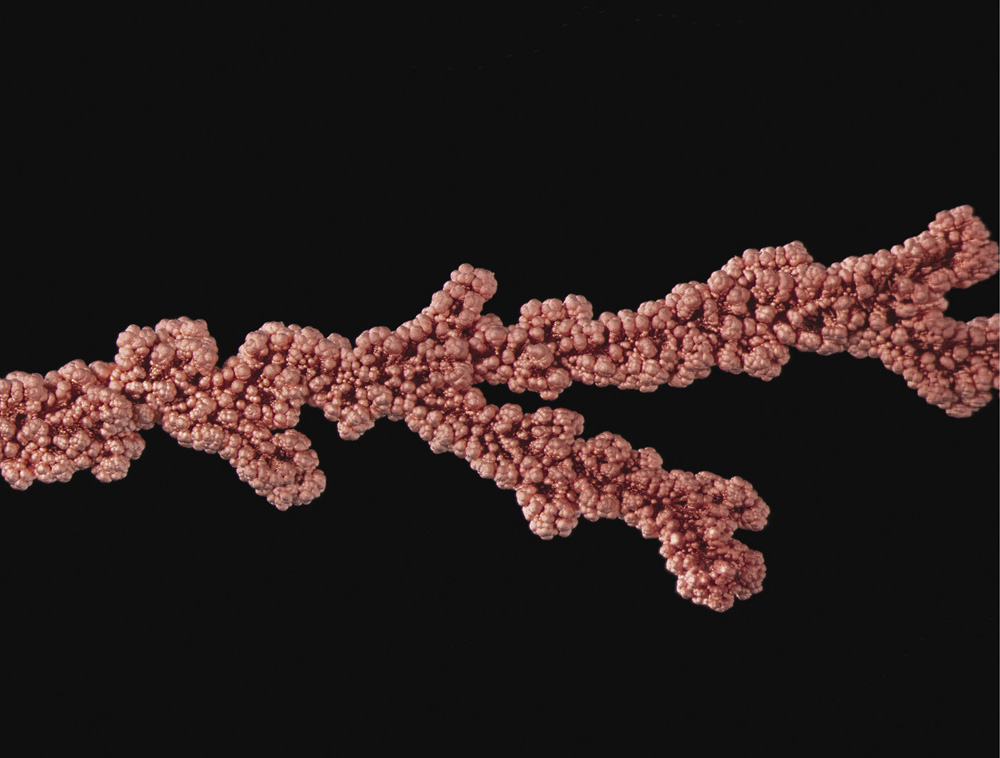
A close-up view of branched copper crystals made by electrochemical deposition
This on its own sounds like a recipe for a random mass of branches: more like an oak than a Christmas tree. But what makes branches in dendritic growth of metals and crystals split off at particular angles is the underlying symmetry of the crystal structure itself: the way the atoms and molecules are packed geometrically, as we saw in chapter 2. This biases the direction in which the branches will sprout. The hexagonality of the snowflake, then, is a consequence of the hexagonal packing of water molecules in ice. Some other dendritic patterns in crystal growth have branches at other angles—in particular, some sprout at right angles, because the atoms in the crystal are packed into square arrays.
It wasn't until the 1980s that all this was understood—that there was a proper theory of how snowflakes form. Even now there are aspects of the process that remain mysterious. It's hard to explain, for example, why all six of the points can look so identical. Why should that be, if the branches are just sprouting by chance, albeit biased to grow in “hexagonal” directions? Now, the truth is that many snowflakes are not so symmetrical after all: the six arms look rather similar in overall shape, but the details differ. If you're used to seeing pictures of perfectly symmetrical snowflakes, it's because those are often the ones selected, since they look the most beautiful. All the same, such “perfect” snowflakes clearly do exist—and it's not obvious how each branch in such structures seems to “know” what the others are doing.
“It's not obvious how each branch in a snowflake seems to ‘know’ what the others are doing.”
What's more, not all snowflakes have arms with the classic Christmas-tree shape. They can have a wide variety of forms. Sometimes the arms are decorated with more blocky, hexagon-shaped plates of ice. Sometimes the entire snowflake grows like a simple hexagon. And depending on the temperature and humidity of the air in which they grow, snow crystals can have quite different microscopic shapes, in particular columns and prisms with hexagonal cross-sections. Many different forms of snowflake might appear in a single snowfall, depending on the precise conditions in the air within which any given crystal formed. You might, then, think of snowflakes as nature's frozen yet ephemeral record of its tiny variations from one place to another.





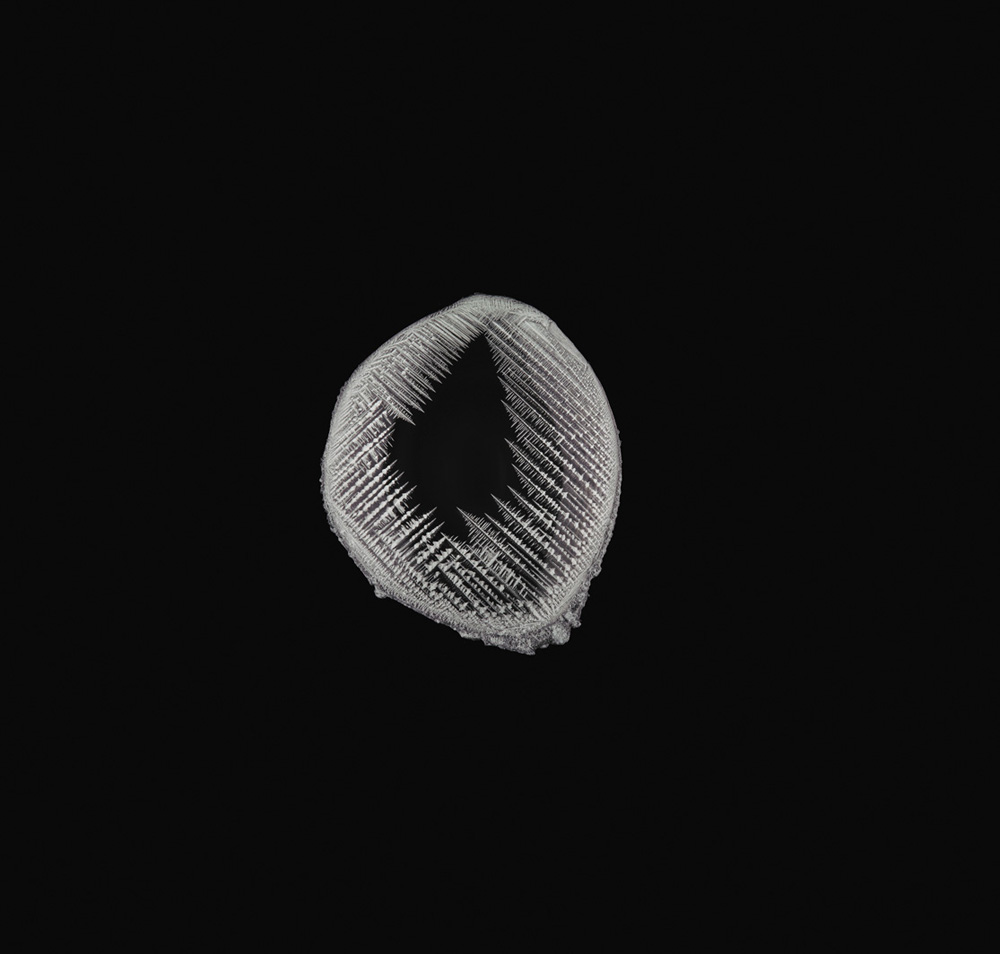


Snowflake-like dendritic growth of silver crystals in a displacement reaction of silver nitrate and copper


Dendritic, snowflake-like growth is not the norm for crystals. As we saw in the last chapter, more commonly they form prism-shaped lumps, their faces and edges not ramified and jagged but on the contrary smooth and flat. Why sometimes one, and sometimes the other?
It's largely a matter of the speed of growth—or to put it another way, how big the “driving force” is for crystallization to happen at all. In general, if you cool a molten metal slowly below its freezing point, it will freeze slowly into regular, blocky crystals. Dendritic growth, in contrast, tends to happen when the molten metal is plunged suddenly to temperatures well below the freezing point, so that the solidification happens all in a rush. Scientists would say that the first process happens “close to equilibrium”—the system in which growth occurs isn't too far from its most stable state (that is, crystalline), while the second happens “far from equilibrium.”
Snowflakes are an example of the kind of complex, patterned structures that often appear in processes happening far from their equilibrium state; in chapter 10 we will encounter some others. This fine balance of complexity and regularity arising far from equilibrium is a feature also of life itself. It is, then, after all not entirely coincidental that snowflakes and dendritic growth put us in mind of trees and flowers—of matter animated by life.
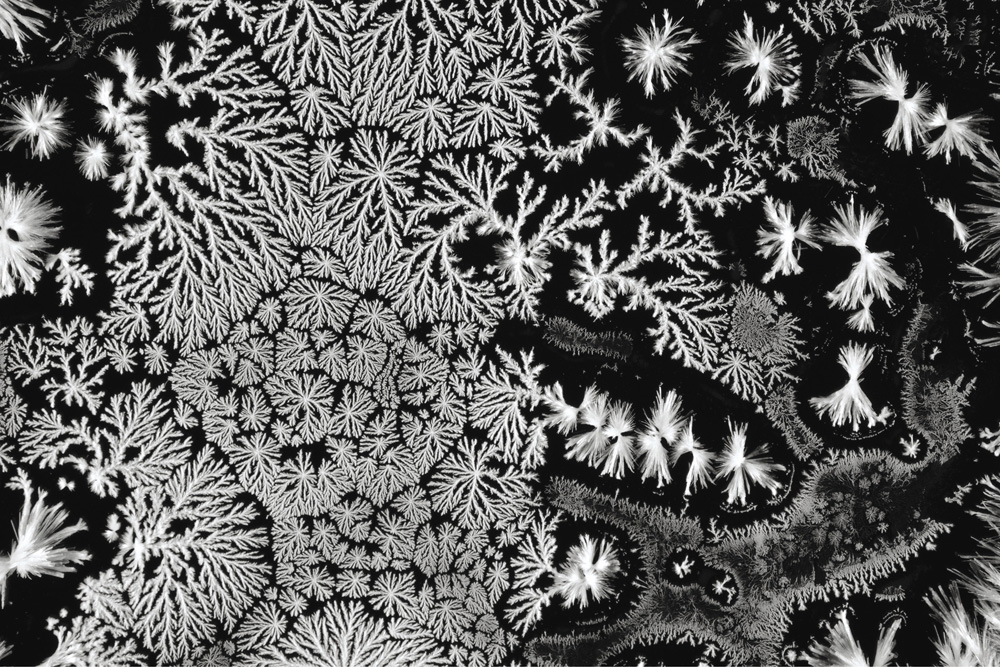
The same can be said of a different type of branching crystal growth. Some types of porous rock, such as sandstone, may be laced with delicate frondlike structures that are sometimes mistaken for fossil plants but are instead nothing but inorganic minerals of dark material. These go by the name of “mineral dendrites”—confusingly, because they are not strictly speaking the product of dendritic growth of the sort that makes snowflakes. The overlapping terms were coined at different times, and again they indicate just how insistently a comparison with the branches of plants recommends itself.
You might also see shapes like these in electrodeposition, where the metals sprout in vegetative profusion like coral on a rocky outcrop of the seabed—a process described in chapter 6. If you zoom in close to these branched electrodeposits, they are typically made from tiny, prism-shaped crystals thrown together at all manner of angles, like a random scattering of bricks cemented in place. Why don't they simply develop into a single, dense clump? Why all the branching?
The answer lies in another of those growth instabilities. Think of the surface of the deposit as growing by accumulating more particles on its surface. These particles drift through the solution at random until they strike the surface, where they stick at once in whatever position and orientation they happen to have.
Now suppose again that, purely by chance, a small bump appears on the surface where slightly more particles have happened to alight than elsewhere. Precisely because the bump protrudes a little from the surface, other particles will be more likely to hit it first. And so it will accumulate particles at a faster rate, and will grow more quickly than the rest of the surface. Here again is that element of feedback: the more it grows, the faster it grows.






Mineral dendrites of a manganese salt formed naturally inside a rock


And again, this process of finger formation recurs on the surface of the metal finger itself, making it sprout side branches. But in this case, there is nothing to bias the direction of the branches, because the particles—the little crystallites, say—just stick wherever they strike. So, the branching is all jumbled, and the result is a dense, random forest of branches. This process goes by the name of diffusion-limited aggregation, and it underpins the formation both of mineral dendrites—where the dark-colored mineral, typically a salt of manganese, precipitates from a salt-rich fluid percolating through the porous stone—and of randomly branched electrodeposits.
These recursively branching forms tend to look much the same at several different powers of magnification. Zoom in closer and you see more of the fine detail, but it looks much the same as the ramified form visible at lower magnification. A structure like this, which retains the same appearance at different scales of magnification, is called a fractal. Many snowflakes are also fractals, their branches repeating at finer scales like the fronds of a fern—but they are fractals of a peculiarly regular, geometric sort. In nature, fractal forms are common, and usually more irregular than the snowflake: the crenellations of a coastline, say, or the ever-finer branches of a river network or a system of blood vessels in the body.
“Many snowflakes are fractals, their branches repeating at finer scales like the fronds of a fern.”
Fractals are one of nature's fundamental forms, and chemistry can supply them in a simple process of electrically induced crystallization, spreading from an electrode like a root pushing through the soil or a tree spreading its branches to embrace the sunshine. “Nature,” wrote the American transcendentalist Ralph Waldo Emerson, “is an endless combination and repetition of a very few laws. She hums the old well-known air through innumerable variations.”

Mineral dendrites of a manganese salt formed naturally inside a rock

Further reading
- Ball, P. Nature's Patterns: Branches. Oxford: Oxford University Press, 2009.
- Bentley, W., and W. Humphreys. Snow Crystals. New York: Dover, 1962.
- Libbrecht, K. G. The Snowflake: Winter's Secret Beauty. Stillwater, MN: Voyageur Press, 2003. See also www.snowcrystals.com
- Mandelbrot, B. The Fractal Geometry of Nature. New York: W. H. Freeman, 1984.
- Stewart, I. What Shape Is a Snowflake? Magical Numbers in Nature. London: Weidenfeld and Nicolson, 2001.
For some chemists, beauty lies in the shape and clarity of a crystal or in the color or texture of a pigment. For others it is expressed by synthetic molecular structures in the shapes of the Platonic or Archimedean solids, such as cubane, dodecahedrane, and buckminsterfullerene, prized for their symmetry, simplicity, and uniformity. These structures—and many others into the bargain—are simply beautiful and beautifully simple.
One of the really beautiful hallmarks of chemistry is its ability to keep reinventing itself. This endearing virtue places the chemist in the same arena as a painter, sculptor, or musical composer. I found myself acting out this privileged role, starting back in the 1980s, as a maker of mechanically interlocked molecules, held together by a brand-new kind of bond called the mechanical bond. These molecules have not only played a central role in molecular nanotechnology but have also initiated a shift toward more aesthetically pleasing and artistically attractive ways of illustrating molecules in the scientific literature. Such eye-catching representations are now part of the chemical lexicon. A molecule with two or more interlocked rings we call a catenane, derived from the Latin word for “chain,” and a molecule comprised of a rod threaded through one or more rings, with the ends blocked by bulky groups, we call a rotaxane, derived from the Latin words for “wheel” and “axle.”
Nature was using mechanical bonds long before we humans came on the scene, for example in the form of catenanes and knots of DNA. Nature executes the chemistry of the mechanical bond with an elegance, complexity, and beauty that will remain a source of inspiration to synthetic chemists for centuries to come.
Nobel Laureate in Chemistry, 2016