The Druidic Syllabus, II: Advanced
Behind all the other mysteries stood the tree that gave the Druids their name. According to Pliny, the Druids planted groves of oak, ‘and they perform none of their religious rites without using its leaves’. This is one of several hints of Hellenic influence. The oak-wreathed head of the Greek sun god appears on many Celtic coins, and the oak groves of the Druids may have been designed for the kind of divination familiar to Odysseus, who journeyed to the remote shrine of Dodona ‘to hear the lofty oak express the will of Zeus’ in the rustling of its leaves. But an institution of such geographical and philosophical scope would have had many origins. In the never-ending realms of folklore, the branches of the oak point in all directions like the knotted fingers of a witch. The Celtic oak may have been a cosmic tree that spanned the three worlds, like the ash tree, Yggdrasil, of Norse mythology, or a relic of local, prehistoric beliefs that had been codified by the Druids. Caesar believed that Druidism had been ‘discovered’ (‘reperta’) in Britain (p. 10), and the preponderance of oak in English woodland may indeed have given rise to local cults that have left their trace in the hundreds of ‘oak’ place names that share an etymological origin with ‘Druid’: Darroch, Darwen, Derby, Derwent, etc.
The keys to Celtic mysteries usually lie in an observable reality rather than in a vague superstition. Oak is one of the best firewoods (‘Oaken logs, if dry and old / Keep away the winter’s cold’), and one of the best ways in which to get to know a tree is to prepare it for burning. Divine utterances are no longer perceptible in the rustling of oak leaves, but faces can still be seen in that most anthropomorphic of trees. Many of those faces have Celtic features. A few hours of attacking fallen oak branches with a bow saw and a splitting maul will produce a representative selection of ancient Celtic art works. The snags and antlered ends of dead branches are the beaked monsters of Celtic fibulae and flagon handles. The oval knots are the eyes of a Celtic god or the war-trumpet called a carnyx, and the pendant clusters of male flowers and the knobbly burrs that turn into beautiful whorls in the planed wood are the nodules and incrustations on gold armbands and torcs. Where a branch has cracked and pulled away from the trunk, the sinewy labyrinth of circles looks like the pattern book of a Celtic artist.
‘The Celtic Druids investigated to the very highest point the Pythagorean philosophy’, said Hippolytus of Rome; they practise divination ‘from calculations and numbers by the Pythagorean art’.* The oak was an object of particular scrutiny. This was not the pagan ‘tree worship’ that Christian missionaries would try to eradicate, nor was it simply an artistic imitation of natural phenomena. Celtic art was a scientific attempt to decipher the secrets of creation, ‘for offerings should be rendered to the gods by philosophers who are experienced in the nature of the divine and who speak, as it were, the same language as the gods’ (Diodorus Siculus). In order to learn that language, they ‘conducted investigations and attempted to explain the system of interrelations [or, in a variant text, ‘the inner laws’] and the highest secrets of nature’ (Timagenes).
The Pythagoreans believed that the universe could be explained by numbers. Two and a half thousand years before particle physics and the bio-inspired algorithms of computer science, a belief in the power of numbers was considered by most educated people to be a form of mystical obfuscation, but in the tangle of the oak grove there were shapes that seemed to obey the geometrical laws that had been described by Pythagoras. The contortions of the oak and the leaves and berries of the mistletoe appear in almost every imaginable Celtic object: a shield cover, the phalera of a harness, a cooking pot, a coin. Even when the design seems to be complete, the whole picture is never revealed. The principle of construction is always hidden, as it is in nature, and these swirls and mazy lines are easily mistaken for the meanderings of an individual artist’s fantasy.

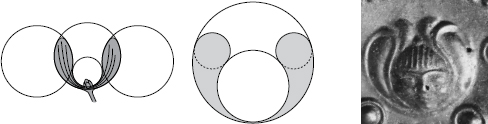
25. The geometry of the mistletoe
The face appears on a bronze phalera (harness ornament) of the fifth century BC from Horovicky (Czech Republic).
These cunning designs, which could evoke the elegant dance of a plant’s leaves, the orbiting of spheres or the harmonious muscles of a horse, were one of the first great flowerings of the scientific spirit and one of the most disciplined and classical of ancient arts. The forms that remained in use over a large part of the Western world for almost a thousand years were probably created by artists under instruction from the Druids: in the forges of Bibracte, the apprentices would have learned to recognize the fibrous qualities of wrought iron and the alarming volatility of gold. The mythological connotations of these shapes are unknown, but the language they spoke is not so deeply encrypted that it can never be recovered.
The geometrical basis of early Celtic art was recognized only recently, and much of the work remains to be done. For the time being, a hypothetical Druidic design manual could begin almost anywhere – with a face in the British Museum, for instance, on the handle mounts of a ‘bucket’ or funerary urn that was placed in the grave of a Kentish Briton at about the time of Caesar’s invasion (fig. 28). The secret of this emaciated, alien face has remained intact. But a Druid would have known that just as the stars and planets were regulated by an invisible system of circles and ellipses, the face was the visible witness of a complex pattern. Once the pattern has been deduced, its deeper meaning emerges: the mouth, the source of eloquence and prophetic utterance, forming the lowest extremity of the figure, turns out to be the true centre of the design. It also occupies the centre of four Pythagorean triangles, which, for reasons that will shortly be mentioned, means that this face that watched over the cremated remains of a man or a woman of Cantium contained the fragments of a compass by which mortals could find their way on Middle Earth and in the world beyond.

26. The geometry of Celtic art
Once the geometrical pattern has been deduced from the phalera (top), it proves to be applicable to many other objects. Phalera from the Somme-Bionne chariot burial (France), 450–400 BC. Flower from an inner panel of the Gundestrup Cauldron (Denmark), 175–150 BC. Bronze appliqué from a flagon, Dürrnberg bei Hallein (Austria), 400–350 BC.

27. Gold coin of the Parisii
A gold coin of the Parisii tribe, first century BC. These coins can be analysed in various ways. Two implicit patterns are shown on the right. The symbols are astronomical. The horse itself may represent the constellation of Ursa Major.
It used to be said – and sometimes still is – that the ‘symbols’ of Celtic art were ‘copied’ from other civilizations by Iron Age artists who laboured under the same cerebral limitations that Victorian scholars attributed to savages: ‘The Celt was a clever adaptor, but weak as an innovator’ (this was written in 1980). To the Celts themselves, knowing from their observations of nature and the heavens that eternal truths are not presented in an instantly comprehensible form, the humanized gods of Greece and Rome were childishly literal idols. When Brennos, the leader of the Celtic expedition to Delphi, entered a shrine and saw gods of wood and stone standing about like real people, he burst out laughing.

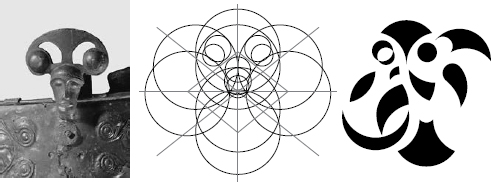
Some phrases of the gods’ language can be deciphered in the pink-granite basin of Bibracte (first century BC). So much information is stored in its subtle curves that it might have served as a teaching aid. The basin is the geometrical result of two circles, overlapping at one-fifth of their diameters. Lines drawn from the centre of the oval to the centre of one of the circles and to a point of intersection form a Pythagorean triangle – a right-angled triangle with lengths that are a Pythagorean triad: 3, 4 and 5. Pythagoras himself may have invented the figure, but there is no trace of this geometrical experiment in the Pythagorean books of Euclid’s Elements (c. 300 BC), and the basin may be the witness to an independent tradition of Druid mathematics.
28. The face on the Aylesford Bucket
The face on the Aylesford Bucket (c. 50 BC), and the compass-drawn design that produced it. Other characteristically Celtic shapes that can be derived from the same design are shown on the right.
The oval formed by two intersecting circles was not primarily a symbol but the materialization of mathematical truths. Later, when the intrinsic logic of the figure had been forgotten, it became an esoteric emblem: the ‘mandorla’ (almond) or ‘vesica piscis’ (fish bladder) was the secret insignia of early Christians. In Christian iconography, it was associated with the vulva and used to frame the baby Jesus or the Madonna. It may have had a similar sexual connotation for the Druids, which would account for the use of red clay and pink granite. (The granite closest to Bibracte was grey; the pink granite came from the Mont de Fer, eight kilometres further east.) Perhaps, like its Christian equivalent, the sky-reflecting pool was the portal that linked the upper, middle and lower worlds, and the portal through which every human being passed.
The apprentice Druids and Druidesses would have explored this smooth, mysterious object in all its surprising detail. The female shape that later contained the Christ child emerging from his mother’s womb was an Iron Age scientific calculator. Though it hardly bears comparison with the Acropolis or St Peter’s Basilica, the pink-granite basin of Bibracte is one of the most remarkable religious monuments of Europe. (It also happens to be the best-preserved Celtic stone structure.) The Pythagorean triangle has two angles of 53.13°. This was, to within four-fifths of a degree, the angle of the solstice sun at Bibracte. Accuracy of this order in the measurement of angles is often thought to have been unattainable without theodolites, but here, in one of the clearest numerical utterances of the gods – two intersecting circles and a Pythagorean triangle – is proof that solar pathways could be measured quite simply. The fact that this solstice angle happens to be the angle produced by the sacred Pythagorean triad of 3, 4 and 5 must have struck the Druid mathematicians of Bibracte as a particularly auspicious coincidence.
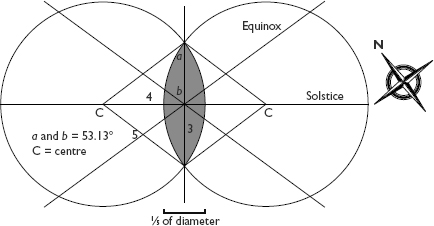
29. The pink-granite basin at Bibracte

Having acquired a working knowledge of the language of the gods, the apprentices would have been ready to perform duties at the temple. They would have learned how to celebrate the four great festivals and to calculate their dates,* and the correct manner in which to hold a sacrificial victim (one hand around the knee, the other clutching the waist). (Fig. 30.)
Until the early 1980s, it was assumed that most Celtic temples were clearings in a wood. Then the eight-year-long excavation of a third-century BC Bellovacian shrine at Gournay-sur-Aronde changed the imagined scene completely. Celtic temples are now known to have been solid wooden structures with ambulatories and well-defined areas marked off for particular forms of sacrifice. A Greek traveller would have recognized the arrangement and perhaps some of the ceremonies. In the centre of the temple, aligned on the solstice or the equinox, was a hollow altar lined with wood. Inside, the putrefying remains of sacrificial victims – pigs, sheep, dogs or humans – filtered down into the lower world. Other victims hung like tapestries on the outer palisade: their flesh would be taken up to heaven by scavengers and the elements, which is why the Celtic and Iberian soldiers on Hannibal’s expedition insisted on leaving their comrades’ bodies unburned on the battlefield.

30. The Gundestrup Cauldron (detail), c. 175–150 BC
The Greek terms for the two forms of sacrifice were ‘chthonic’ (‘under the earth’) and ‘Olympian’ or ‘ouranian’ (‘heavenly’). Each temple was a double portal: some spirits passed from the world of the living to Albos, the ‘white’ world of the heavens; others descended to Dumnos, the world of ‘darkness’ or ‘the deep’. The temples were, in effect, an early form of church, with more pungent and literal reminders of death than stale incense and a musty crypt.
The vestments of the ‘oak sages’ themselves are depicted on the silver Gundestrup Cauldron, which was discovered in a Danish peat bog in 1891. It shows scenes of Druidic rites and unidentified Celtic myths. The tall figure who plunges a sacrificial victim into a vat wears what an expert on Celtic dress has described as ‘tight trousers akin to cycling shorts’. The close-knit ribbing of the costume is also reminiscent of the thin, vertical striations of oak wood. The tasselled skull-cap looks like the cup and stalk of the acorn of the pedunculate oak, and the pattern on the laced slippers recalls the stylized oak-leaves of Celtic designs. This is, to all appearances, a man dressed to look like an oak. In a costume made of brown sheep’s wool, a Druid, or a pupil in Druid school uniform, could have passed through the oak wood less noticeably than a deer. Modern Druids who wish to resemble their predecessors should consider exchanging their white robes for oak-patterned Lycra, oak-leaf slippers, acorn caps for winter and oak-leaf headdresses for summer.
As Druidism spread to the remotest parts of Europe, new temples had to be built. A Druid would be expected to direct the architectural operation according to the will of the gods. Since the gods spoke in riddles, it is not surprising that there is something odd about the shape of Celtic temples. The four corner posts and ditches typically describe a clumsily drawn square or rectangle. These ‘subrectangular enclosures’ seem to have been laid out by a sloppy surveyor who always managed to put at least one of the corners in the wrong place. A British structural archaeologist, analysing Celtic enclosures in the south of England, noted in 2009 that ‘nothing was quite square’, and asked, ‘So were [the Celts] just rubbish at surveying?’ ‘Either prehistoric southern England was a land of botchers and bodgers, or they were doing it deliberately and systematically. I chose the latter option and called the phenomenon “systematic irregularity”.’
Five years earlier, in an article on Celtic temples in the Vexin region to the north-west of Paris, a French archaeologist had pondered the same problem. He noticed that, in every case, a line drawn through the major axis of the skewed rectangle produced two triangles that were mirror images of each other. These peculiar shapes appeared to have been produced by attaching a loose length of rope to two poles, then stretching it out on either side to define the other two points. The pattern did after all have a geometrical rationale, but, in characteristically Druidic fashion, the underlying principle was concealed. Like the labyrinthine oak, the apparently lopsided ground plan contained a logic that was visible only to initiates.
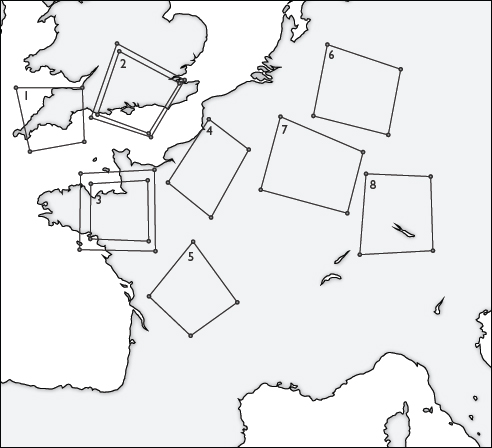
31. Celtic subrectangular enclosures
Examples of Celtic subrectangular enclosures in England, France and Germany. Key: 1. South Cadbury. 2. Casterley Camp. 3. Oisseau-le-Petit. 4. Bruyères-sur-Oise. 5. Arnac-la-Poste. 6. Hardheim. 7. Oberesslingen. 8. Holzhausen.
The question remains: why such an awkward design? Was it simply a geometrical puzzle or a hasty way of drawing an approximate rectangle? But there are many easier ways in which to draw a four-sided figure, and why would carpenters and roofers whose wooden houses were greater feats of engineering than any Greek or Roman temple have tolerated such a poorly drawn and inconvenient plan?
Something spectacular lies behind the configuration of these enigmatic structures, but it was only after a self-taught course in Druidic science that I realized what it was. As philosophers ‘bound together in fellowships according to the rules and example of Pythagoras’ (Timagenes), the Druids would have been aware of the heavenly shape that Pythagoras was said to have been the first to recognize. The sun’s apparent motion against the background of stars over the course of a year describes a slanted circle called the ecliptic. This is the elliptical loop along which the planets and the twelve constellations of the zodiac appear. For a culture that attached such importance to the motion of the sun, this would have been a crucial discovery.
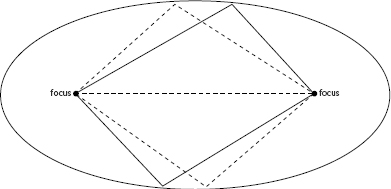
32. The ground plan of a Celtic temple
To draw the ground plan of a Celtic temple, attach a thread to two pins placed at the foci; drag the thread with a pencil and, keeping it taut, trace out the ellipse. NB: the pink-granite basin at Bibracte is an oval, which is distinct from an ellipse.
The surveying operation involving two poles and a length of rope is the simplest method of drawing an ellipse. Though there was nothing on the ground to show it, these apparently defective rectangles are the geometrical figures that define the yearly course of the sun. The temples and other sacred enclosures that were once a prominent feature of the landscape were constructed as though the heavenly ellipse surrounded them. And just as the line of the solstice sun had been materialized in the Via Heraklea, this other solar pathway was mapped out on the earth in thousands of places from Bavaria to the Atlantic Ocean.
This was the shape of worship in Europe for hundreds of years. The path of the sun was implicit in the precinct of the temple, and the points of the four Celtic festivals might have been marked at the correct points of the zodiacal ellipse like Stations of the Cross. In this virtual ellipse, the shadow of a Druidic rite can be seen. The Celts, like most cultures, performed ceremonies of circumambulation. According to Posidonius, they turned to the right (that is, to the south) when honouring their gods, which was also the direction in which St Patrick and other Celtic saints turned when they consecrated a church or a well, processing around the site ‘deisiol’ (‘to the right’ or ‘sunwise’). The invisible ellipse of the Celtic temple suggests that the saints were following not just the direction of the sun but its path through the heavens.
The Druids’ arcane observance of ‘the inner laws of nature’ has functioned extremely well as a cloaking device. It has defeated the archaeological computer programs that were designed to identify significant patterns of post-holes, and this entire chapter in the history of religion and architecture has remained hidden for two thousand years. Until now, the string construction of the ellipse was thought to have been unknown in the West before the late sixteenth century ad. The unostentatious cleverness of the Druids has made it possible to go on believing that the Romans, with their tidy squares and rectangles, were a technically superior civilization. It is no wonder that these masters of invisibility would make such a fearsome resistance force when they reassembled in Britain after the conquest of Gaul.

Twenty years was probably barely enough time for a complete Druidic education. No doubt there were many sub-disciplines and areas of specialization. Some Druids studied the medicinal properties of plants – ‘selago’ (fir club moss), whose smoke could heal a sick eye, ‘samolus’ (brookweed), which preserved swine and cattle from disease, and mistletoe, which was an antidote to any poison. Apart from the elephantine blasts produced by a reconstituted carnyx, ancient Celtic music is entirely lost, but Pythagoras’s investigations of harmonic intervals would certainly have formed part of the curriculum. The Celtic bards played an instrument similar to the lyre, and Druid musicians may have composed the acoustic equivalents of geometrical designs.
Druids who contemplated a career in politics would have studied civil and criminal jurisprudence, including the legal corollaries of a belief in the transmigration of souls (the settlement of debts was sometimes delayed until the next world, and money was lent in the expectation that it would be repaid by the deceased). They studied the internal administration of the order and the protocol for electing a new chief Druid. Like Diviciacus, some Druids became experts in intertribal affairs, and, although they never bore arms, they had to be familiar with political and military strategy: ‘Often, when two armies approach each other in battle with swords drawn and spears thrust forward, these philosophers step forth between them and cause them to cease, as though casting a spell over wild beasts.’ (Diodorus Siculus)*
One day, many years after arriving at the school, an apprentice, already on the verge of middle age, would stand under the night sky, perhaps where a viewing platform had been set up on the eastern edge of Bibracte. This was the most scientifically advanced part of the course. It would enable the Druid to predict the future and to prepare Middle Earth for the advent of the gods:
The Druids discuss and impart to the youth many things regarding the stars and their motion, the size of the universe and the earth, the nature of things, and the power and majesty of the immortal gods. (Caesar, De Bello Gallico, VI, 14)
Pomponius Mela says something very similar, but in a form that seems to echo the original triad: ‘Hi terrae mundique magnitudinem et formam, motus caeli ac siderum et quid dii velint, scire profitentur.’ (‘They profess to know the size and shape of the earth and the universe, the motion of the sky and the stars, and what the gods want.’)
This is the triadic equation of mathematical divination: take the geodetic data (the spherical shape of the earth, its size and its zones of latitude), factor in the necessary astronomical observations (eclipses, shadow lengths, solstice angles), and the result of the calculation will reveal the will of the gods – ‘quid dii velint’ (specifically, how to orient the altar, the direction in which to attack an enemy, the most auspicious trajectory for a tribal migration).
Unlike those of the Babylonians, the Druids’ astronomical observations have not survived, except, by implication, in the five-year solar-lunar calendar engraved on a sheet of bronze that was dug out of a field in the foothills of the Jura. But their observations can be inferred from the system of Mediolana and the long-distance roads of Gaul. Studying the theorems of Pythagoras, the Druids would have been as familiar with Greek science as the Celts of the Mediterranean, and since theirs was the only intellocracy in Europe, and the only fellowship of scientists organized on such a scale, they may have added to what the Greeks had taught them. Caesar’s verb ‘disputant’ (‘they discuss’) shows that this was not a fossilized body of knowledge. Like university professors, the Druids taught, but they also conducted research and modified their teachings to take account of the latest stage of scholarly debate.
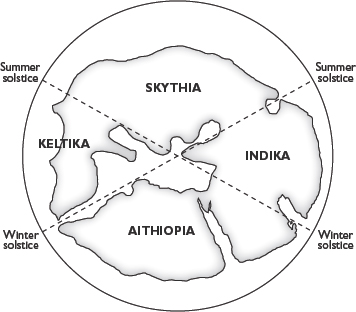
33. Division of the world by Ephorus, c. 350 BC
They would have been acquainted with klimata and the division of the inhabited world by Ephorus (c. 350 BC) into four zones based on the solstice angles of the sun.
Aristotle would have been known to them as a leading authority on the teachings of Pythagoras but also as the philosopher who had refined the system of klimata.
The diagonals or solstice lines are the lines known to sailors as rhumb lines: the navigator chooses a bearing and holds to that bearing until the destination is reached. The centre of the Aristotelian earth was Rhodes, where the angle of the solstice sun in the fourth century BC happened to be exactly sixty degrees or one-sixth of a circle. (This is the angle of the solstice lines shown in the two diagrams above.) To an observer in more northerly latitudes, the angle was noticeably different, but on the geometrical evidence of the pink-granite basin and countless everyday objects of Celtic art, the Druids had the means of adapting the Aristotelian system to Celtic climes. They also had a huge, uninterrupted land mass on which to practise their navigation and to match their movements to the calculated will of the gods.
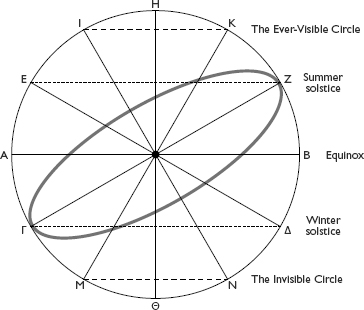
34. Division of the world by Aristotle
Aristotle, Meteorology (350 BC), II, 6, and the zodiacal path identified by Pythagoras. The twelve directions were conventionally named after the winds that blew from those quarters. The ‘Ever-Visible’ and ‘Invisible’ Circles (referring to the setting of stars) are the Arctic and Antarctic Circles.
The newly qualified Druid who descended from the mountain after twenty years would know that the gods were present in every corner of the natural world, that nature itself was a temple and Middle Earth a mirror of the upper world. The temple presided over by the Druid was a material expression of those truths, a form of obedience to the immortal gods. Like the botanizing, star-gazing parish priests of later centuries, the Druid would continue to observe and record ‘the inner laws of nature’. And, as branches of the sacred oak, possessing the secrets of the earth and the sky, and knowing their motions and dimensions, thousands of Druids all over Europe would contribute to the building of another temple so vast that it would turn Middle Earth into a world in which the gods would be at home. This was the miraculous efficiency of which Eratosthenes and other lone scientists could only dream.
* Pythagoras taught in the sixth century BC. ‘Pythagorean’ is the interpretation of classical, non-Celtic writers, who saw similarities between Druidism and Hellenic philosophies, just as later writers perceived analogies with Brahmanism. These filiations are neither implausible nor provable.
* The four Celtic festivals occur on the ‘cross-quarter days’, halfway between solstice and equinox: Samhain – winter solstice – Imbolc – vernal equinox – Beltane – summer solstice – Lughnasadh – autumn equinox.
* This may have been a function of female Druids: Plutarch and Polyaenus attributed the power to stop battles to ‘Celtic women’.