
8
The Rise of the Replicators
Machines to make machines and machines to make minds
‘“The androids,” she said, “are lonely too.”’
Do Androids Dream of Electric Sheep?,
Philip K. Dick, 1968
The odd angles, harsh lighting and wobbly movements of the handcam give the video of a 3D printer at work the air of an amateur porn film. In an odd sort of way it is, for the video shows a machine caught, in flagrante, reproducing. The ‘Snappy’ is a RepRap – a self-copying 3D printer – that is able to print around 80 per cent of its own parts.1 If a printer part breaks, you can replace it with a spare that you printed earlier. For the cost of materials – the plastic filament that is melted and extruded by a printer costs $20–50 a kilo – you can print most of another printer for a friend. Just a handful of generic metal parts such as bolts, screws and motors and the electronic components must be bought to complete assembly.
Engineer and mathematician Adrian Bowyer first conceived the idea he calls ‘Darwinian Marxism’ in 2004 – that eventually everyone’s home will be a factory, producing anything they want (as long as it can be made out of plastic, anyway). Engineers at Carleton University in Ottawa are working on filling in that stubborn last 20 per cent, to create a printer that can fully replicate itself even if you don’t have a DIY shop handy. Specifically, they are thinking about using only materials that can be found on the surface of the moon. Using a RepRap as their starting point, the researchers have begun to design a rover that will print all its parts and the tools it needs to copy itself using only raw materials harvested in situ by, for example, smelting lunar rock in a solar furnace.2 They have also made experimental motors and computers with McCulloch–Pitts-style artificial neurons to allow their rover to navigate. Semiconductor-based electronic devices would be practically impossible to make on the moon, so in a charming 1950s twist, they plan to use vacuum tubes instead. ‘When I came across RepRap, although it was a modest start, for me it was catalytic,’ says Alex Ellery, who leads the group. ‘What began as a side project now consumes my thoughts.’3
Once they are established on the moon, Ellery’s machines could multiply to form a self-expanding, semi-autonomous space factory making … virtually anything. They might, for example, print bases ready for human colonizers – or even, as Ellery hopes, help to mitigate global warming by making swarms of miniature satellites that can shield us from solar radiation or beam energy down to Earth.4
The inspiration for all these efforts and more is a book entitled Theory of Self-reproducing Automata; its author, John von Neumann. In between building his computer at the IAS and consulting for the government and industry, von Neumann had begun comparing biological machines to synthetic ones. Perhaps, he thought, whatever he learned could help to overcome the limitations of the computers he was helping to design. ‘Natural organisms are, as a rule, much more complicated and subtle, and therefore much less well understood in detail, than are artificial automata,’ he noted. ‘Nevertheless, some regularities which we observe in the organization of the former may be quite instructive in our thinking and planning of the latter.’5
After reading the McCulloch and Pitts paper describing artificial neural networks, von Neumann had grown interested in the biological sciences and corresponded with several scientists who were helping to illuminate the molecular basis of life, including Sol Spiegelman and Max Delbrück. In his usual way, von Neumann dabbled brilliantly, widely and rather inconclusively in the subject but intuitively hit upon a number of ideas that would prove to be fertile areas of research for others. He lectured on the mechanics of the separation of chromosomes that occurs during cell division. He wrote to Wiener proposing an ambitious programme of research on bacteriophages, conjecturing that these viruses, which infect bacteria, might be simple enough to be studied productively and large enough to be imaged with an electron microscope. A group of researchers convened by Delbrück and Salvador Luria would over the next two decades shed light on DNA replication and the nature of the genetic code by doing exactly that – and produce some of the first detailed pictures of the viruses.
One of von Neumann’s most intriguing proposals was in the field of protein structure. Most genes encode proteins, molecules which carry out nearly all important tasks in cells, and are the key building block of muscles, nails and hair. Though proteins were being studied extensively in the 1940s, no one knew what they looked like, and the technique that was eventually used to study them, X-ray crystallography, was still in its infancy. The shape of a protein can be deduced from the pattern of spots produced by firing X-rays at crystals of it. The problem was, as von Neumann quickly realized, the calculations that would need to be done to reconstruct the protein’s shape far exceeded the capacity of the computers available at the time. In 1946 and 1947, he met with renowned American chemist Irving Langmuir and the brilliant mathematician Dorothy Wrinch, who had developed the ‘cyclol’ model of protein structure. Wrinch pictured proteins as interlinked rings, a conjecture that would turn out to be wrong, but von Neumann thought that scaling up the experiment some hundred-million-fold might shed light on the problem. He proposed building centimetre-scale models using metal balls and swapping X-rays for radar technology, then comparing the resulting patterns with those from real proteins. The proposal was never funded but demonstrates how far von Neumann’s interests ranged across virtually every area of cutting-edge science. In the event, advances in practical techniques as well as theoretical ones – and a great deal of patience – would be required before X-ray crystallography began to reveal protein structures – as it would, starting in 1958.
From 1944, meetings instigated by Norbert Wiener helped to focus von Neumann’s thinking about brains and computers. In gatherings of the short-lived ‘Teleological Society’, and later in the ‘Conferences on Cybernetics’, von Neumann was at the heart of discussions on how the brain or computing machines generate ‘purposive behaviour’. Busy with so many other things, he would whizz in, lecture for an hour or two on the links between information and entropy or circuits for logical reasoning, then whizz off again – leaving the bewildered attendees to discuss the implications of whatever he had said for the rest of the afternoon. Listening to von Neumann talk about the logic of neuro-anatomy, one scientist declared, was like ‘hanging on to the tail of a kite’.6 Wiener, for his part, had the discomfiting habit of falling asleep during discussions and snoring loudly, only to wake with some pertinent comment demonstrating he had somehow been listening after all.
By late 1946, von Neumann was growing frustrated with the abstract model of the neuron that had informed his EDVAC report on programmable computers a year earlier. ‘After the great positive contribution of Turing-cum-Pitts-and-McCulloch is assimilated, the situation is rather worse than before,’ he complained in a letter to Wiener.
Indeed, these authors have demonstrated in absolute and hopeless generality, that … even one, definite mechanism can be ‘universal’. Inverting the argument: Nothing that we may know or learn about the functioning of the organism can give, without ‘microscopic’, cytological work any clues regarding the further details of the neural mechanism … I think you will feel with me the type of frustration that I am trying to express.
Von Neumann thought that pure logic had run its course in the realm of brain circuitry and he, who had set a record bill for broken glassware while studying at the ETH, was sceptical that fiddly, messy lab work had much to offer. ‘To understand the brain with neurological methods,’ he says dismissively,
seems to me about as hopeful as to want to understand the ENIAC with no instrument at one’s disposal that is smaller than about 2 feet across its critical organs, with no methods of intervention more delicate than playing with a fire hose (although one might fill it with kerosene or nitroglycerine instead of water) or dropping cobblestones into the circuit.
To avoid what he saw as a dead end, von Neumann suggested the study of automata be split into two parts: one devoted to studying the basic elements composing automata (neurons, vacuum tubes), the other to their organization. The former area was the province of physiology in the case of neurons, and electrical engineering for vacuum tubes. The latter would treat these elements as idealized ‘black boxes’ that would be assumed to behave in predictable ways. This would be the province of von Neumann’s automata theory.
The theory of automata was first unveiled in a lecture in Pasadena on 24 September 1948, at the Hixon Symposium on Cerebral Mechanisms in Behaviour and published in 1951.7 Von Neumann had been thinking about the core ideas for some time, presenting them first in informal lectures in Princeton two years earlier. His focus had shifted subtly. Towards the end of his lecture, von Neumann raises the question of whether an automaton can make another one that is as complicated as itself. He notes that at first sight, this seems untenable because the parent must contain a complete description of the new machine and all the apparatus to assemble it. Although this argument ‘has some indefinite plausibility to it,’ von Neumann says, ‘it is in clear contradiction with the most obvious things that go on in nature. Organisms reproduce themselves, that is, they produce new organisms with no decrease in complexity. In addition, there are long periods of evolution during which the complexity is even increasing.’ Any theory that claims to encompass the workings of artificial and natural automata must explain how man-made machines might reproduce – and evolve. Three hundred years earlier, when the philosopher René Descartes declared ‘the body to be nothing but a machine’ his student, the twenty-three-year-old Queen Christina of Sweden, is said to have challenged him: ‘I never saw my clock making babies’.8 Von Neumann was not the first person to ask the question ‘can machines reproduce?’ but he would be the first to answer it.
At the heart of von Neumann’s theory is the Universal Turing machine. Furnished with a description of any other Turing machine and a list of instructions, the universal machine can imitate it. Von Neumann begins by considering what a Turing-machine-like automaton would need to make copies of itself, rather than just compute. He argues that three things are necessary and sufficient. First, the machine requires a set of instructions that describe how to build another like it – like Turing’s paper tape but made of the same ‘stuff’ as the machine itself. Second, the machine must have a construction unit that can build a new automaton by executing these instructions. Finally, the machine needs a unit that is able to create a copy of the instructions and insert them into the new machine.
The machine he has described ‘has some further attractive sides’, notes von Neumann, with characteristic understatement. ‘It is quite clear’ that the instructions are ‘roughly effecting the functions of a gene. It is also clear that the copying mechanism … performs the fundamental act of reproduction, the duplication of the genetic material, which is clearly the fundamental operation in the multiplication of living cells.’ Completing the analogy, von Neumann notes that small alterations to the instructions ‘can exhibit certain typical traits which appear in connection with mutation, lethally as a rule, but with a possibility of continuing reproduction with a modification of traits’.9 Five years before the discovery of the structure of DNA in 1953, and long before scientists understood cell replication in detail, von Neumann had laid out the theoretical underpinnings of molecular biology by identifying the essential steps required for an entity to make a copy of itself. Remarkably, von Neumann also correctly surmised the limits of his analogy: genes do not contain step-by-step assembly instructions but ‘only general pointers, general cues’ – the rest, we now know, is furnished by the gene’s cellular environment.
These were not straightforward conclusions to reach in 1948. Erwin Schrödinger, by now safely ensconced at the Dublin Institute for Advanced Studies, got it wrong. In his 1944 book What Is Life?,10 which inspired, among others, James Watson and Francis Crick to pursue their studies of DNA, Schrödinger explored how complex living systems could arise – in seeming contradiction with the laws of physics. Schrödinger’s answer – that chromosomes contain some kind of ‘code-script’ – failed to distinguish between the code and the means to copy and implement the code.11 ‘The chromosome structures are at the same time instrumental in bringing about the development they foreshadow,’ he says erroneously. ‘They are law-code and executive power – or, to use another simile, they are architect’s plan and builder’s craft all in one.’
Few biologists appear to have read von Neumann’s lecture or understood its implications if they did – surprising, considering many of the scientists von Neumann met and wrote to during the 1940s were physicists with an interest in biology. Like Delbrück, many would soon help elucidate the molecular basis of life. That von Neumann was wary of journalists sensationalizing his work and too busy to popularize the theory himself probably did not help (Schrödinger, by contrast, had the lay reader in mind as his audience).
One biologist who did read von Neumann’s words soon after their publication in 1951 was Sydney Brenner. He was later part of Delbrück’s coterie of bacteriophage researchers and worked with Crick and others in the 1960s to crack the genetic code. Brenner says that when he saw the double helix model of DNA in April 1953, everything clicked into place. ‘What von Neumann shows is that you have to have a mechanism not only of copying the machine but of copying the information that specifies the machine,’ he explains. ‘Von Neumann essentially tells you how it’s done … DNA is just one of the implementations of this.’12 Or, as Freeman Dyson put it, ‘So far as we know, the basic design of every microorganism larger than a virus is precisely as von Neumann said it should be.’13
In lectures over the next few years and an unfinished manuscript, von Neumann began to detail his theory about automata – including a vision of what his self-reproducing machines might look like. His work would be meticulously edited and completed by Arthur Burks, the mathematician and electrical engineer who had worked on both the ENIAC and von Neumann’s computer project. The resulting book, Theory of Self-reproducing Automata, would only appear in 1966.14 The first two accounts of von Neumann’s ideas in print would appear in 1955, though neither was the work of automata theory’s progenitor. The first of these was an article in Scientific American15 by computer scientist John Kemeny, who later developed the BASIC programming language (and was Einstein’s assistant at the IAS when Nash called on him). The second, which appeared in Galaxy Science Fiction later that year, was by the author Philip K. Dick, whose work would form the basis of films such as Blade Runner (1982), Total Recall (1990 and 2012) and Minority Report (2002).16 His ‘Autofac’ is the tale of automatic factories set on consuming the Earth’s resources to make products that no one needs – and more copies of themselves. Dick closely followed von Neumann’s career, and his story had been written the year before the Scientific American piece about automata appeared.17

Kemeny’s sober write-up, entitled ‘Man Viewed as a Machine’, is barely less sensational than the sci-fi story. ‘Are we, as rational beings, basically different from universal Turing machines?’ he asks. ‘The usual answer is that whatever else machines can do, it still takes a man to build the machine. Who would dare to say that a machine can reproduce itself and make other machines?’ Kemeny continues, sounding deliciously like a 1950s B movie voice-over. ‘Von Neumann would. As a matter of fact, he has blue-printed just such a machine.’
The first artificial creatures von Neumann imagined float on a sea of ‘parts’ or ‘organs’. There are eight different types of part, with four devoted to performing logical operations. Of these, one organ is a signal-generator, while the other three are devoted to signal-processing. The ‘stimulus’ organ fires whenever one of its two inputs receives a signal, a ‘coincidence’ organ fires only when both inputs do, and a fourth ‘inhibitory’ organ fires only if one input is active and the other is not. With these parts, the automaton can execute any conceivable set of computations.
The remaining parts are structural. There are struts, and two organs that can cut or fuse struts into larger arrangements. Lastly there is muscle, which contracts when stimulated and can, for instance, bring two struts together for welding or grasping.18 Von Neumann suggests that the automaton might identify parts through a series of tests. If the component it has caught between its pincers is transmitting a regular pulse, for example, then it is a signal-transmitter; if it contracts when stimulated, it is muscle.
The binary instruction tape that the automaton will follow – its DNA – is encoded, ingeniously, using the struts themselves. A long series of struts joined into a saw-tooth shape forms the ‘backbone’. Each vertex can then have a strut attached to represent a ‘one’ or be left free for a ‘zero’. To write or erase the tape, the automaton adds or removes these side-chains.
From the parts that von Neumann describes it is possible to assemble a floating autofac, fully equipped to grab from the surrounding sea whatever parts it needs to make more, fertile autofacs – complete with their own physical copy of ‘strut DNA’. A strut broken or added by mistake is a mutation – often lethal, sometimes harmless and occasionally beneficial.
Von Neumann was not satisfied with this early ‘kinematic’ model of self-replication. The supposedly elementary parts from which the automaton is made are actually quite complex. He wondered if simpler mathematical organisms might spawn themselves. Did self-reproduction require three dimensions, or would a two-dimensional plane suffice? He spoke to Ulam, who had been toying with the idea of automata confined to a two-dimensional crystalline lattice, interacting with their neighbours in accordance with a simple set of rules. Inspired, von Neumann developed what would become known as his ‘cellular’ model of automata.
Von Neumann’s self-reproducing automata live on an endless two-dimensional grid. Each square or ‘cell’ on this sheet can be in one of twenty-nine different ‘states’, and each square can only communicate with its four contiguous neighbours. This is how it works.
– Most squares begin in a dormant state but can be brought to life – and later ‘killed’– by the appropriate stimulus from a neighbour.
– There are eight states for transmitting a stimulus – each can be ‘on’ or ‘off’, receive inputs from three sides and output the signal to the other.
– A further eight ‘special’ transmission states transmit signals that ‘kill’ ordinary states, sending them back into the dormant state. These special states are in turn reduced to dormancy by a signal from an ordinary transmission state.
– Four ‘confluent’ states, which transmit a signal from any neighbouring cell to any other with a delay of two time units. These can be pictured as consisting of two switches, a and b. Both start in the ‘off’ position. When a signal arrives, a turns on. Next, the signal passes to b, which turns on, while a returns to the ‘off’ position unless the cell has received another signal. Finally, b transmits its signal to any neighbouring transmission cells able to receive it.
– Lastly, a set of eight ‘sensitized’ states can morph into a confluent or transmission state upon receiving certain input signal sequences.
Using this animate matrix, von Neumann will build a behemoth. He begins by combining different cells to form more complex devices. One such ‘basic organ’ is a pulser, which produces a pre-set stream of pulses in response to a stimulus. Another organ, a decoder, recognizes a specific binary sequence and outputs a signal in response. Other organs were necessary because of the limitations imposed by working in two dimensions. In the real world, if two wires cross, one can safely pass over the other. Not so in the world of von Neumann’s cellular automaton, so he builds a crossing organ to route two signals past each other.
Then von Neumann assembles parts to fulfil the three roles that he has identified as being vital for self-reproduction. He constructs a tape from ‘dormant’ cells (representing ‘0’) and transmission cells (representing ‘1’).19 Adding a control unit that can read from and write in tape cells, von Neumann is able to reproduce a universal Turing machine in two dimensions. He then designs a constructing arm which snakes out to any cell on the grid, stimulates it into the desired state then withdraws.
At this point, von Neumann’s virtual creature slipped its leash and overcame even his prodigious multitasking abilities. Starting in September 1952, he had spent more than twelve months on the manuscript, which was by now far longer than he had imagined would be necessary to finish the task. According to Klára, he intended to return to his automata work after discharging various pressing government advisory roles – but he never would. Ill health would overtake him within sight of his goal, and the extraordinary edifice would only be completed years after his death by Burks, who carefully followed von Neumann’s notes to piece together the whole beast.
The complete machine fits in an 80x400-cell box but has an enormous tail, 150,000 squares long, containing the instructions the constructor needs to clone itself. Start the clock, and step by step the monster starts work, reading and executing each tape command to produce a carbon copy of itself some distance away. The tentacular constructing arm grows until it reaches a pre-defined point in the matrix, where it deposits row upon row of cells to form its offspring. Like the RepRaps it would one day inspire, von Neumann’s automaton builds by depositing each layer on the next until assembly is finished whereupon the arm retracts back to the mother, and its progeny is free to begin its own reproductive cycle. Left to its own devices, replication continues indefinitely, and a growing line of automata tracks slowly across the vastness of cellular space into infinity.

Or at least that is what Burks hoped would happen. When Theory of Self-reproducing Automata was published in 1966, there was no computer powerful enough to run von Neumann’s 29-state scheme, so he could not be sure that the automaton he helped design would replicate without a hitch. The first simulation of von Neumann’s machine, in 1994, was so slow that by the time the author’s paper appeared the following year, their automaton had yet to replicate.20 On a modern laptop, it takes minutes. With a little programming know-how, anyone can watch the multiplying critters von Neumann willed into being by the force of pure logic over half a century ago. They are also witnessing in action the very first computer virus ever designed, and a milestone in theoretical computer science.
Von Neumann’s self-reproducing automata would usher in a new branch of mathematics and, in time, a new branch of science devoted to artificial life.21 One thing stood in the way of the revolution that was to come – the first man-made replicator was over-designed. One could, with a small leap of faith, imagine the cellular automaton evolving. One could not, however, imagine such a complex being ever emerging from some sort of digital primordial slime by a fortuitous accident. Not in a million years. And yet the organic automatons that von Neumann was aping had done exactly that. ‘There exists,’ von Neumann wrote, ‘a critical size below which the process of synthesis is degenerative, but above which the phenomenon of synthesis, if properly arranged, can become explosive, in other words, where synthesis of automata can proceed in such a manner that each automaton will produce other automata which are more complex and of higher potentialities than itself.’22 Could a simpler automaton – ideally much simpler – ever be shown to generate, over time, something so complex and vigorous that only the most committed vitalist would hesitate to call it ‘life’? Soon after Theory of Self-reproducing Automata appeared, a mathematician in Cambridge leafed through the book and became obsessed with exactly that question. The fruit of his obsession would be the most famous cellular automaton of all time.
John Horton Conway loved to play games and, in his thirties, managed to secure a salaried position that allowed him to do just that.23 His early years in academia, a phase of his life he called ‘The Black Blank’, were stubbornly devoid of greatness. He had achieved so little he worried privately he would lose his lectureship.
That all changed in 1968, when Conway began publishing a series of remarkable breakthroughs in the field of group theory, findings attained by contemplating symmetries in higher dimensions. To glimpse Conway’s achievement, imagine arranging circles in two dimensions so that there is as little space between them as possible. This configuration is known as ‘hexagonal packing’; lines joining the centres of the circles will form a honeycomb-like network of hexagons. There are exactly twelve different rotations or reflections that map the pattern of circles back onto itself – so it is said to have twelve symmetries. What Conway discovered was a sought-after, rare group of symmetries for packing spheres in twenty-four dimensions. ‘Before, everything I touched turned to nothing,’ Conway said of this moment. ‘Now I was Midas, and everything I touched turned to gold.’24
‘Floccinaucinihilipilification’, meaning ‘the habit of regarding something as worthless’, was Conway’s favourite word. It was how he thought fellow mathematicians felt about his work. After discovering the symmetry group that was soon named after him, as tradition decreed, Conway was free to indulge his whims with abandon. One of those whims was making up mathematical games.

With a gaggle of graduate students, Conway was often found hunched over a Go grid in the common room of the mathematics department, where they placed and removed black and white counters according to rules he and his entourage invented. Von Neumann’s scheme called for twenty-nine different states. ‘It seemed awfully complicated,’ Conway says. ‘What turns me on are things with a wonderful simplicity.’25 He whittled down the number to just two – each cell could either be dead or alive. But whereas the state of a cell in von Neumann’s scheme was determined by its own state and that of its four nearest neighbours, Conway’s cell communicated with all eight of its neighbours, including the four touching its corners.
Each week, Conway and his gang tinkered with the rules that determined whether cells would be born, survive or perish. It was a tricky balancing act: ‘if the death rule was even slightly too strong, then almost every configuration would die off. And conversely, if the birth rule was even a little bit stronger than the death rule, almost every configuration would grow explosively.’26
The games went on for months. One board perched on a coffee table could not contain the action, so more boards were added until the game crept slowly across the carpet and threatened to colonize the whole common room. Professors and students would be on their hands and knees, placing or removing stones during coffee breaks, and coffee breaks would sometimes last all day. After two years of this, the players hit a sweet spot. Three simple rules created neither bleak waste nor boiling chaos, but interesting, unpredictable variety. They were:
- Every cell with two or three live neighbours survives.
- A cell with four or more live neighbours dies of overcrowding. A cell with fewer than two live neighbours dies of loneliness. (In either case, the counter is removed from the board.)
- A ‘birth’ occurs when an empty cell has exactly three neighbours. (A new counter is placed in the square.)
Stones were scattered, the rules applied, and generation after generation of strange objects morphed and grew, or dwindled away to nothing. They called this game ‘Life’.
The players carefully documented the behaviour of different cellular constellations. One or two live cells die after a single generation, they noted. A triplet of horizontal cells becomes three vertical ones, then flashes back to the horizontal and continues back and forth indefinitely. This is a ‘blinker’, one of a class of periodic patterns called ‘oscillators’. An innocent-looking cluster of five cells called an ‘R-pentomino’ explodes into a shower of cells, a dizzying display seemingly without end. Only after months of following its progeny did they discover it stabilized into a fixed pattern some 1,103 generations later. One day in the autumn of 1969, one of Conway’s colleagues called out to the other players: ‘Come over here, there’s a piece that’s walking!’ On the board was another five-celled creature that seemed to be tumbling over itself, returning to its original configuration four generations later – but displaced one square diagonally downwards. Unless disturbed, the ‘glider’, as it was dubbed, would continue along its trajectory for ever. Conway’s automata had demonstrated one characteristic of life absent from von Neumann’s models: locomotion.

Conway assembled a chart of his discoveries and sent them to his friend, Martin Gardner, whose legendary ‘Mathematical Games’ column in Scientific American had acquired a cult following among puzzlers, programmers, sceptics and the mathematically inclined. When Gardner’s column about Life appeared in October 1970, letters began to pour into the mail room, some from as far afield as Moscow, New Delhi and Tokyo. Even Ulam wrote in to the magazine, later sending Conway some of his own papers on automata. Time wrote up the game. Gardner’s column on Life became his most popular ever. ‘All over the world mathematicians with computers were writing Life programs,’ he recalled.

I heard about one mathematician who worked for a large corporation. He had a button concealed under his desk. If he was exploring Life, and someone from management entered the room, he would press the button and the machine would go back to working on some problem related to the company!27
Conway had smuggled a trick question into Gardner’s column to tantalize his readers. The glider was the first piece he needed to build a Universal Turing machine within Life. Like von Neumann’s immensely more complicated cellular automaton, Conway wanted to prove that Life would have the power to compute anything. The glider could carry a signal from A to B. Missing, however, was some way of producing a stream of them – a pulse generator. So Conway conjectured that there was no configuration in Life that would produce new cells ad infinitum and asked Gardner’s readers to prove him wrong – by discovering one. There was a $50 prize on offer for the first winning entry, and Conway even described what the faithful might find: a ‘gun’ that repeatedly shoots out gliders or other moving objects or a ‘puffer train’, a moving pattern that leaves behind a trail. The glider gun was found within a month of the article appearing. William Gosper, a hacker at MIT’s Artificial Intelligence Laboratory, quickly wrote a program to run Life on one of the institute’s powerful computers. Soon, Gosper’s group found a puffer train too. ‘We eventually got puffer trains that emitted gliders which collided together to make glider guns which then emitted gliders but in a quadratically increasing number,’ Gosper marvelled. ‘We totally filled the space with gliders.’28
Conway had his signal generator. He quickly designed Life organisms capable of executing the basic logical operations and storing data.29 Conway did not bother to finish the job – he knew a Turing machine could be built from the components he had assembled. He had done enough to prove that his automaton could carry out any and all computations, and that amazing complexity could arise in a system far simpler than that of von Neumann.30 And he went a step further than even von Neumann would have dared. Conway was convinced that Life could support life itself. ‘It is no doubt true that on a large enough scale Life would generate living configurations,’ he asserted. ‘Genuinely living. Evolving, reproducing, squabbling over territory. Writing Ph.D theses.’31 He did, however, concede that this act of creation might need the game to be played on a board of unimaginable proportions – perhaps bigger than those of the known universe.

To Conway’s everlasting chagrin, he would be remembered best as Life’s inventor. Search ‘Conway’s Game of Life’ in Google today, and flashing constellations of squares appear in one corner and begin rampaging across the screen, a testament to the game’s enduring fascination.
Conway’s achievements delighted automata aficionados, many of whom had been ploughing a lonely furrow. A key cluster of these isolated enthusiasts were based at the University of Michigan, where Burks had in 1956 established an interdisciplinary centre, the Logic of Computers Group, that would become a Mecca for scientists fascinated with the life-like properties of these new mathematical organisms. They shared Conway’s belief that extraordinarily complex phenomena may be underpinned by very simple rules. Termites can build fabulous mounds several metres tall, but, as renowned biologist E. O. Wilson notes, ‘no termite need serve as overseer with blueprint in hand’.32
The Michigan group would run some of the first computer simulations of automata in the 1960s, and many off-shoots of automata theory would trace their origins here.33 One of the first in a stream of visionaries to pass through the doors of the group was Tommaso Toffoli, who started a graduate thesis on cellular automata there in 1975. Toffoli was convinced there was a deep link between automata and the physical world. ‘Von Neumann himself devised cellular automata to make a reductionistic point about the plausibility of life being possible in a world with very simple primitives,’ Toffoli explained. ‘But even von Neumann, who was a quantum physicist, neglected completely the connections with physics – that a cellular automata could be a model of fundamental physics.’34
Perhaps, Toffoli conjectured, the complex laws of physics might be rewritten more simply in terms of automata. Might the strange realm of quantum physics be explained as a product of interactions between von Neumann’s mathematical machines, themselves obeying just a few rules? The first step towards proving that would be to show that there existed automata that were ‘reversible’. The path that the universe has taken to reach its current condition can theoretically be traced backwards (or forwards) to any other point in time (as long as we have complete knowledge of its state now). None of the cellular automata that had been invented, however, had this property. In Conway’s Life, for example, there are many different configurations that end in an empty board. Starting from this blank slate, it is impossible to know which cells were occupied when the game began. Toffoli proved for his PhD thesis that reversible automata did exist and, moreover, that any automaton could be made reversible by adding an extra dimension to the field of play (so, for example, there is a three-dimensional version of Life that is reversible).35
As he cast about for a job, Toffoli was approached by Edward Fredkin, a successful tech entrepreneur who had headed MIT’s pioneering artificial intelligence laboratory. Fredkin was driven by a belief that irresistibly drew him to Toffoli’s work. ‘Living things may be soft and squishy. But the basis of life is clearly digital,’ Fredkin claimed. ‘Put it another way – nothing is done by nature that can’t be done by a computer. If a computer can’t do it, nature can’t.’36 These were fringe views even in the 1970s, but Fredkin could afford not to care. He was a millionaire many times over thanks to a string of successful computer ventures and had even bought his own Caribbean island. Unafraid of courting controversy, Fredkin once appeared on a television show and speculated that, one day, people would wear nanobots on their heads to cut their hair. When he contacted Toffoli, Fredkin was busy assembling a group at MIT to explore his interests – particularly the idea that the visible manifestations of life, the universe and everything were all the result of a code script running on a computer. Fredkin offered Toffoli a job at his new Information Mechanics Group. Toffoli accepted.
The MIT group rapidly became the new nerve centre of automata studies. One of Toffoli’s contributions to the field would be to design, with computer scientist Norman Margolus, a computer specifically to run cellular automata programs faster than even the supercomputers of the time. The Cellular Automata Machine (CAM) would help researchers ride the wave of interest triggered by Conway’s Life. Complex patterns blossomed and faded in front of their eyes as the CAM whizzed through simulations, speeding discoveries they might have missed with their ponderous chuntering lab machines. In 1982, Fredkin organized an informal symposium to nurture the new field at his idyllic Caribbean retreat, Moskito Island (nowadays owned by British tycoon Richard Branson). But there was trouble in paradise, in the shape of a young mathematician by the name of Stephen Wolfram.
Wolfram cuts a divisive figure in the scientific world. He won a scholarship to Eton but never graduated. He went to Oxford University but, appalled by the standard of lectures, he dropped out. His next stop was the California Institute of Technology (CalTech), where he completed a PhD in theoretical physics. He was still only twenty. He joined the IAS in 1983 but left academia four years later after founding Wolfram Research. The company’s flagship product, Mathematica, is a powerful tool for technical computing, written in a language he designed. Since its launch in 1988, millions of copies have been sold.
Wolfram began to work seriously on automata theory at the IAS. His achievements in the field are lauded – not least by himself – and he is dismissive of his predecessors. ‘When I started,’ he told journalist Steven Levy, ‘there were maybe 200 papers written on cellular automata. It’s amazing how little was concluded from those 200 papers. They’re really bad.’37
Like Fredkin, Wolfram thinks that the complexity of the natural world arises from simple computational rules – possibly just one rule – executed repeatedly.38 Wolfram guesses that a single cellular automaton cycling through this rule around 10400 times would be sufficient to reproduce all known laws of physics.39 There is, however, one thing the two scientists disagree about: who came up with the ideas first.40
Fredkin insists he discussed his theories of digital cosmogenesis with Wolfram at the meeting in the Caribbean, and there catalysed his incipient interest in cellular automata. Wolfram says he discovered automata independently, and only afterwards found the work of von Neumann and others describing similar phenomena to those appearing on his computer screen. He traces his interest in automata back to 1972 – when he was twelve years old.41 Sadly, Wolfram says, he did not take his ideas further then because he was distracted by his work on theoretical particle physics. Such assertions would be laughable had Wolfram not, in fact, begun publishing on quantum theory in respectable academic journals from 1975, aged fifteen.
Wolfram’s first paper on cellular automata only appeared in 1983,42 after the Moskito Island meeting, though he says he began work in the field two years earlier.43 He was investigating complex patterns in nature, and was intrigued by two rather disparate questions: how do gasses coalesce to form galaxies, and how might McCulloch and Pitts-style model neurons be assembled into massive artificial neural networks? Wolfram started experimenting with simulations on his computer and was amazed to see strikingly ornate forms appear from computer code a few lines long. He forgot about galaxies and neural networks and started exploring the properties of the curious entities that he had stumbled upon.
The variety of automata Wolfram began playing with were one-dimensional. While von Neumann and Conway’s constructions lived on two-dimensional surfaces, Wolfram’s occupied a horizontal line. Each cell has just two neighbours, one on either side, and is either dead or alive. As with Conway’s Game of Life, the easiest way to understand what Wolfram’s automata are doing is by simulating their behaviour on a computer, with black and white squares for live and dead cells. Successive generations are shown one beneath the other, with the first, progenitor row at the top. As Wolfram’s programs ran, a picture emerged on his screen that showed, line by line, the entire evolutionary history of his automata. He called them ‘elementary cellular automata’ because the rules that determined the fate of a cell were very straightforward.
In Wolfram’s scheme, a cell communicates only with its immediate neighbours, and their states together with its own determine whether it will live or die. Those three cells can be in one of eight possible combinations of states. If ‘1’ represents a live cell and ‘0’ a dead one, these are: 111, 110, 101, 100, 011, 010, 001 and 000. For each of these configurations, a rule dictates what the central cell’s state will be next. These eight rules, together with the starting line-up of cells, can be used to calculate every subsequent configuration of an elementary cellular automaton. Wolfram invented a numbering convention so that all eight rules governing an automaton’s behaviour could be captured in a single number, from 0 to 255. Converting the decimal number to binary gives an eight-digit number that reveals whether the middle cell of each trio will be a ‘1’ or a ‘0’ next.

Wolfram systematically studied all 256 different sets of rules available to his elementary cellular automata, sorting them carefully into groups like a mathematical zoologist.
Some of the rule sets produced very boring results. Rule 255 maps all eight configurations onto live cells, resulting in a dark screen; Rule 0 condemns all cells to death, producing a blank screen. Others resulted in repetitive patterns, for example Rule 250, which maps to the binary number 11111010. Starting from a single black cell, this leads to a widening checkerboard pattern.
A more intricate motif appears when an automaton follows Rule 90. The picture that emerges is a triangle composed of triangles, a sort of repetitive jigsaw puzzle, in which each identical piece is composed of smaller pieces, drawing the eye into its vertiginous depths. This kind of pattern, which looks the same at different scales, is known as a fractal, and this particular one, a Sierpiński triangle, crops up in a number of different cellular automata. In Life, for example, all that is required for the shape to appear is to start the game with a long line of live cells.
Still, pretty as these patterns are, they are hardly surprising. Looking at them, one could guess that a simple rule applied many times over might account for their apparent complexity. Would all elementary cellular automata turn out to produce patterns that were at heart also elementary? Rule 30 would show decisively that they did not. The same sorts of rule are at play with this automaton as with Wolfram’s others – each describes the new colour of the central cell of a triad. The rules can be summarized as follows. The new colour of the central cell is the opposite of that of its current left-hand neighbour except in the two cases where both the middle cell and its right-hand neighbour are white. In this case, the centre cell takes the same colour as its left-hand neighbour. Start with a single black cell as before, and within fifty generations the pattern descends into chaos. While there are discernible diagonal bands on the left-side of the pyramid, the right side is a froth of triangles.
Wolfram checked the column of cells directly below the initial black square for any signs of repetition. Even after a million steps, he found none. According to standard statistical tests, this sequence of black and white cells is perfectly random. Soon after Wolfram presented his findings, people began sending him seashells with triangular markings that bore an uncanny resemblance to the ‘random’ pattern generated by Rule 30. For Wolfram, it was a strong hint that apparent randomness in nature, whether it appears on conch shells or in quantum physics, could be the product of basic algorithms just a few lines long.
Wolfram unearthed even more remarkable behaviour when he explored Rule 110. Starting from a single black square as before, the pattern expands only to the left, forming a growing right-angled triangle (rather than a pyramid like Rule 30) on which stripes shifted and clashed on a background of small white triangles. Even when Wolfram started with a random sequence of cells, ordered structures emerged and ‘moved’ left or right through the lattice. These moving patterns suggested an intriguing possibility. Were these regularities capable of carrying signals from one part of the pattern to another, like the ‘gliders’ in Conway’s Life? If so, this incredibly rudimentary one-dimensional machine might also be a universal computer. Mathematician Matthew Cook, who worked as Wolfram’s research assistant in the 1990s, would prove it was.44 Given enough space and time and the right inputs, Rule 110 will run any program – even Super Mario Bros.



Wolfram developed a classification system for automata based on computer experiments of these kinds. Class 1 housed automata which, like rule 0 or 255, rapidly converged to a uniform final state no matter what the initial input. Automata in Class 2 may end up in one of a number of states. The final patterns are all either stable or repeat themselves every few steps, like the fractal produced by Rule 90. In Class 3 are automata that, like Rule 30, show essentially random behaviour. Finally, Class 4 automata, like Rule 110, produce disordered patterns punctuated by regular structures that move and interact. This class is home to all cellular automata capable of supporting universal computation.45
The stream of papers that Wolfram was producing on automata was causing a stir, but not everyone approved. Attitudes at the IAS had not moved on much from von Neumann’s day, and the idea that meaningful mathematics could be done on computers – Wolfram’s office was chock full of them – was still an anathema. Wolfram’s four-year post came to an end in 1986, and he was not offered the chance to join the illustrious ranks of the permanent staff. A year later, busy with his new company he paused his foray into the world of cellular automata – only to stage a dramatic return to the field in 2002, with A New Kind of Science.46 That book, the result of ten years of work done in hermit-like isolation from the wider scientific community, is Wolfram’s first draft of a theory of everything.

The 1,280-page tome starts with characteristic modesty. ‘Three centuries ago science was transformed by the dramatic new idea that rules based on mathematical equations could be used to describe the natural world,’ he declares. ‘My purpose in this book is to initiate another such transformation.’ And that transformation, he explained, would be achieved by finding the single ‘ultimate rule’ underlying all other physical laws – the automaton to rule them all, God’s four-line computer program. Wolfram had not found that rule. He was not even close. But he did tell a journalist he expected the code to be found in his lifetime – perhaps by himself.47
The book presents in dazzling detail the results of Wolfram’s painstaking investigations of cellular automata of many kinds. His conclusion is that simple rules can yield complex outputs but adding more rules (or dimensions) rarely adds much complexity to the final outcome. In fact, the behaviour of all the systems he surveys falls into one of the four classes that he had identified years earlier. Wolfram then contends similar simple programs are at work in nature and marshals examples from biology, physics and even economics to make his case. He shows, for example, how snowflake-like shapes can be produced with an automaton that turns cells on a hexagonal lattice black only when exactly one neighbour is black. Later, he simulates the whorls and eddies in fluids using just five rules to determine the outcome of collisions between molecules moving about on a two-dimensional grid. Similar efforts produce patterns resembling the branching patterns of trees and the shapes of leaves. Wolfram even suggests the random fluctuations of stocks on short timescales might be a result of simple rules and shows a one-dimensional cellular automaton roughly reproduces the sort of spiking prices seen in real markets.
The most ambitious chapter contains Wolfram’s ideas on fundamental physics, encapsulating his thoughts on gravity, particle physics and quantum theory. He argues that a cellular automaton is not the right choice for modelling the universe. Space would have to be partitioned into tiny cells, and some sort of a timekeeper would be required to ensure that every cell updates in perfect lockstep. Wolfram’s preferred picture of space is a vast, sub-microscopic network of nodes, in which each node is connected to three others. The sort of automaton that he thinks underlies our complex physics is one that changes the connections between neighbouring nodes according to some simple rules – for instance, transforming a connection between two nodes into a fork between three. Apply the right rule throughout the network billions of times and, Wolfram hopes, the network will warp and ripple in exactly the ways predicted by Einstein in his general theory of relativity. At the opposite end of the scale, Wolfram conjectures that elementary particles like electrons are the manifestations of persistent patterns rippling through the network – not so different from the gliders of rule 110 or Life.
The problem with Wolfram’s models, as his critics were quick to point out, is that it is impossible to determine whether they reflect reality unless they make falsifiable predictions – and Wolfram’s do not (yet). Wolfram hoped that his book would galvanize researchers to adopt his methods and push them further, but his extravagant claim of founding ‘a new kind of science’ got short shrift from many scientists. ‘There’s a tradition of scientists approaching senility to come up with grand, improbable theories,’ Freeman Dyson told Newsweek after the book’s release. ‘Wolfram is unusual in that he’s doing this in his 40s.’48
Disheartened by the reception of the book in scientific circles, Wolfram disappeared from the public eye only to re-emerge almost twenty years later, in April 2020.49 With the encouragement of two young acolytes, physicists Jonathan Gorard and Max Piskunov, his team at Wolfram Research had explored around a thousand universes that emerged from following different rules.50 Wolfram and his colleagues showed that the properties of these universes were consistent with some features of modern physics.
The results intrigued some physicists, but the establishment, in general, was once again unenthusiastic. Wolfram’s habit of belittling or obscuring the accomplishments of his predecessors has garnered a less receptive audience than his ideas otherwise might have had. ‘John von Neumann, he absolutely didn’t see this,’ Wolfram says, insisting that he was the first to truly understand that enormous complexity can spring from automata. ‘John Conway, same thing.’51
A New Kind of Science is a beautiful book. It may prove in time also to be an important one. The jury, however, is still very much out. Whatever the ultimate verdict of his peers, Wolfram had succeeded in putting cellular automata on the map like no one else. His groundwork would help spur those who saw automata not just as crude simulations of life, but as the primitive essence of life itself.
‘If people do not believe that mathematics is simple,’ von Neumann once said, ‘it is only because they do not realize how complicated life is.’52 He was fascinated by evolution through natural selection, and some of the earliest experiments on his five-kilobyte IAS machine involved strings of code that could reproduce and mutate like DNA. The man who sowed those early seeds of digital life was an eccentric, uncompromising Norwegian-Italian mathematician named Nils Aall Barricelli.53
A true maverick, Barricelli was never awarded a doctorate because he refused to cut his 500-page long thesis to a length acceptable to his examiners. He was often on the wrong side of the line that separates visionaries from cranks, once paying assistants out of his own not-very-deep pockets to find flaws in Gödel’s famous proof. He planned, though never finished, a machine to prove or disprove mathematical theorems. Some of his ideas in biology, however, were genuinely ahead of their time. Von Neumann had a proclivity for helping people with big ideas. When Barricelli contacted him to ask for time on the IAS machine, he was intrigued. ‘Mr. Barricelli’s work on genetics, which struck me as highly original and interesting … will require a great deal of numerical work,’ von Neumann wrote in support of Barricelli’s grant application, ‘which could be most advantageously effected with high-speed digital computers of a very advanced type.’
Barricelli arrived in Princeton in January 1953, loosed his numerical organisms into their digital habitat on the night of 3 March 1953 and birthed the field of artificial life. Barricelli believed that mutation and natural selection alone could not account for the appearance of new species. A more promising avenue for that, he thought, was symbiogenesis, in which two different organisms work so closely together that they effectively merge into a single, more complex creature. The idea of symbiogenesis had been around since at least the turn of the twentieth century. For passionate advocates like Barricelli, the theory implies that it is principally cooperation not competition between species that drives evolution.
The micro-universe Barricelli created inside von Neumann’s machine was designed to test his symbiogenesis-inspired hypothesis that genes themselves were originally virus-like organisms that had, in the past, combined and paved the way to complex, multi-cellular organisms. Each ‘gene’ implanted in the computer’s memory was a number from negative to positive 18, assigned randomly by Barricelli using a pack of playing cards.54 His starting configuration was a horizontal row of 512 genes. In the next generation, on the row below, each gene with number, n, produces a copy of itself n places to the right if it is positive, n places to the left if it is negative. The gene ‘2’, for example, occupies the same position on the row beneath it, but also produces a copy of itself two places to the right. This was the act of reproduction. Barricelli then introduced various rules to simulate mutations. If two numbers try to occupy the same square, for example, they are added together and so on. ‘In this manner,’ he wrote, ‘we have created a class of numbers which are able to reproduce and to undergo hereditary changes. The conditions for an evolution process according to the principle of Darwin’s theory would appear to be present.’55
To simulate symbiogenesis, Barricelli changed the rules so that the ‘genes’ could only reproduce themselves with the help of another of a different type. Otherwise, they simply wandered through the array, moving left or right but never multiplying.
The IAS machine was busy with bomb calculations and weather forecasts, so Barricelli ran his code at night. Working alone, he cycled punched cards through the computer to follow the fate of his species over thousands of generations of reproduction. ‘No process of evolution had ever been observed prior to the Princeton experiments,’ he proudly told von Neumann.56
But the experiments performed in 1953 were not entirely successful. Simple configurations of numbers would invade to become the single dominant organism. Other primitive combinations of numbers acted like parasites, gobbling up their hosts before dying out themselves. Barricelli returned to Princeton a year later to try again. He tweaked the rules, so that, for instance, different mutation rules pertained in different sections of each numerical array. Complex coalitions of numbers propagated through the matrix, producing patterns resembling the outputs of Wolfram’s computer simulations decades later. That is no coincidence – Barricelli’s numerical organisms were effectively one-dimensional automata too. On this trip, the punched cards documented more interesting phenomena, which Barricelli likened to biological events such as self-repair and the crossing of parental gene sequences.
Barricelli concluded that symbiogenesis was all important and omnipresent, perhaps on extrasolar planets as well as on Earth. Random genetic changes coupled with natural selection, he argued, cannot account for the emergence of multi-cellular life forms. On that he was wrong, but symbiogenesis is now the leading explanation of how plant and animal cells arose from simpler, prokaryotic organisms. The recent discovery of gene transfer between a plant and an animal (in this case the whitefly Bemisia tabaci) suggests this process is more widespread than was recognized in Barricelli’s day.57

In the sixties, Barricelli evolved numerical organisms to play ‘Tac-Tix’, a simple two-player strategy game played on a four-by-four grid, then, later, chess. The algorithms he developed anticipated machine learning, a branch of artificial intelligence that focuses on applications that improve at a task by finding patterns in data. But perhaps because he was so out of step with mainstream thought, Barricelli’s pioneering work was largely forgotten. Only decades later would the study of numerical organisms be properly revived. The first conference dedicated to artificial life would be held at Los Alamos in September 1987, uniting under one banner scientists working in disciplines as disparate as physics, anthropology and genetics (evolutionary biologist Richard Dawkins was one of around 160 attendees). The ‘Interdisciplinary Workshop on the Synthesis and Simulation of Living Systems’ was convened by computer scientist Christopher Langton, who expressed the aims of the field in terms that would have been familiar to Barricelli. ‘Artificial life is the study of artificial systems that exhibit behaviour characteristic of natural living systems … The ultimate goal,’ Langton wrote, ‘is to extract the logical form of living systems.’58 Los Alamos had birthed in secret the technology of death. Langton hoped that arid spot would also be remembered one day for birthing new kinds of life.
Langton first encountered automata while programming computers in the early 1970s for the Stanley Cobb Laboratory for Psychiatric Research in Boston. When people started running Conway’s Life on the machines, Langton was enthralled and began experimenting with the game himself. His thoughts on artificial life, however, did not begin to coalesce until he was hospitalized in 1975 following a near-fatal hang-gliding accident in North Carolina’s Blue Ridge Mountains. With plenty of time to read, Langton, who had no formal scientific training, recognized where his true interests lay. The following year, he enrolled at the University of Arizona in Tucson and assembled from the courses on offer his own curriculum on the principles of artificial biology. When the first personal computers appeared, he bought one and began trying to simulate evolutionary processes. It was then, while trawling through the library’s shelves, that Langton discovered von Neumann’s work on self-reproducing automata and hit upon the idea of simulating one on his computer.
Langton quickly realized that the 29-state cellular automaton was far too complicated to reproduce with the technology he had to hand. He wrote to Burks, who informed him that Edgar Codd, an English computer scientist, had simplified von Neumann’s design a few years earlier, as part of doctoral work at the University of Michigan. Codd’s 8-state automaton was, like von Neumann’s, capable of universal computation and construction. When Langton found that Codd’s machine was also far too complex to simulate on his Apple II, he dropped those requirements. ‘It is highly unlikely,’ he reasoned later, ‘that the earliest self-reproducing molecules, from which all living organisms are supposed to have been derived, were capable of universal construction, and we would not want to eliminate those from the class of truly self-reproducing configurations.’59
What Langton arrived at after many rounds of simplification were what he called ‘loops’. Each loop is a square-ish doughnut with a short arm jutting out from one corner, resembling a prostrate letter ‘p’. When a loop begins its reproductive cycle, this appendage grows, curling around to form an identical square-shaped loop next to its parent. On completion, the link to the parent is severed, and parent and daughter each grow another arm from a different corner to begin another round of replication. Loops surrounded on all four sides by other loops are unable to germinate new arms. These perish, leaving a dead core surrounded by a fertile outer layer, like a coral reef.
Determined to pursue his thoughts on automata further, Langton searched for a graduate programme that would accept him. He found only one: the Logic of Computers Group founded by Burks. In 1982, aged thirty-three, unusually mature for a graduate student, Langton arrived at the University of Michigan ready to begin his studies. He soon encountered Wolfram’s early research on classifying automata and recognized the work of a kindred spirit. ‘After a paper by Steve Wolfram of Cal Tech – amazing how I screwed around with these linear arrays over a year ago and never imagined that I was working with publishable material,’ he wrote in his journal. ‘Surely, I thinks to myself, this has been done 30 years ago, but No! Some kid out of Cal Tech publishes a learned paper on one dimensional two-state arrays!! What have people been doing all these years?’60

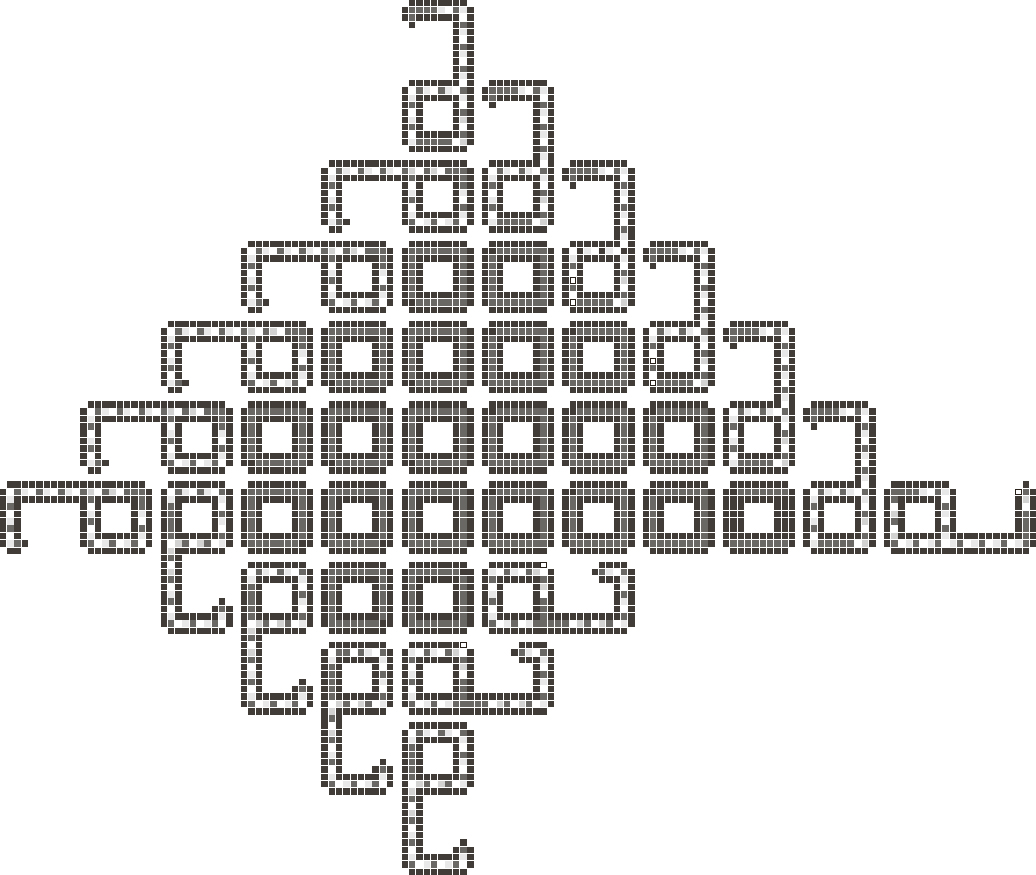
What intrigued Langton most about Wolfram’s system was the question of what tipped a system from one class to another – in particular, from chaos to computation. Langton felt automata able to transmit and manipulate information were closest to the biological automata he wanted to emulate. ‘Living organisms,’ he explained, ‘use information in order to rebuild themselves, in order to locate food, in order to maintain themselves by retaining internal structure … the structure itself is information.’61
Langton’s experiments with a variety of automata led him to propose a sort of mathematical tuning knob which he called a system’s ‘lambda (λ) parameter’.62 On settings of lambda close to zero, information was frozen in repetitive patterns. These were Wolfram’s Class 1 and 2 automata. On the other hand, at the highest values of lambda, close to one, information moved too freely for any kind of meaningful computation to occur. The end result was noise – the output of Wolfram’s Class 3 automata. The most interesting Class 4 automata are poised at a value of lambda that allows information to be both stably stored and transmitted. All of life is balanced on that knife edge ‘below which,’ as von Neumann had put it, ‘the process of synthesis is degenerative, but above which the phenomenon of synthesis, if properly arranged, can become explosive’. And if that tipping point had been found by happy accident on Earth, could it be discovered again by intelligent beings actively searching for it? Langton believed it could – and humanity should start preparing for all the ethical quandaries and dangers that artificial life entailed.
Langton had almost cried tears of joy when he stepped up to deliver his lecture at the Los Alamos conference in 1987. His reflections afterwards were more sombre. ‘By the middle of this century, mankind had acquired the power to extinguish life,’ he wrote. ‘By the end of the century, he will be able to create it. Of the two, it is hard to say which places the larger burden of responsibilities on our shoulders.’63
Langton’s prediction was a little off. Mankind had to wait a decade longer than he envisaged for the first lab-made organism to appear. In 2010, the American biotechnologist and entrepreneur Craig Venter and his collaborators made a synthetic near-identical copy of a genome from the bacterium Mycoplasma mycoides and transplanted it into a cell that had its own genome removed.64 The cell ‘booted up’ with the new instructions and began replicating like a natural bacterium. Venter hailed ‘the first self-replicating species we’ve had on the planet whose parent is a computer’ and though plenty of scientists disagreed that his team’s creation was truly a ‘new life form’, the organism was quickly dubbed ‘Synthia’.65 Six years later, researchers from Venter’s institute produced cells containing a genome smaller than that of any independently replicating organism found in nature. They had pared down the M. mycoides genome to half its original size through a process of trial and error. With just 473 genes, the new microorganism is a genuinely novel species, which they named ‘JCVI-syn3.0a’.66 The team even produced a computer simulation of their beast’s life processes.67
Others hope to go a step further. Within a decade, these scientists hope to build synthetic cells from the bottom up by injecting into oil bubbles called liposomes the biological machinery necessary for the cells to grow and divide.68
Von Neumann’s cellular automata seeded grand theories of everything and inspired pioneers who dared to imagine life could be made from scratch. His unfinished kinematic automaton too has borne fruit. Soon after Kemeny publicized von Neumann’s ideas, other scientists wondered if something like it could be realized not in computer simulations, but in real-life physical stuff. Rather than the ‘soft’ world of biology, their devices were rooted in the ‘hard’ world of mechanical parts, held together with nuts and bolts – ‘clanking replicators’ as nanotechnology pioneer Eric Drexler dubbed them, or the autofacs of Dick’s story.69
Von Neumann had left no blueprint for anyone to follow – his automaton was a theoretical construct, no more than a thought experiment to prove that a machine could make other machines including itself. Consequently, the earliest efforts of scientists to realize kinetic automata were crude, aiming only to show that the ability to reproduce was not exclusively a trait of living things. As geneticist Lionel Penrose noted, the very idea of self-reproduction was so ‘closely associated with the fundamental processes of biology that it carries with it a suggestion of magic’.70 With his son, future Nobel laureate Roger, Penrose made a series of plywood models to show that replication could occur without any hocus-pocus. Each set of wooden blocks had an ingenious arrangement of catches, hooks and levers that were designed to allow only certain configurations to stick together. By shaking the blocks together on a tray, Penrose was able to demonstrate couplings and cleavages that he likened to natural processes such as cell division. One block, for instance, could ‘catch’ up to three others. This chain of four would then split down the middle to form a pair of new two-block ‘organisms’, each of which could grow and reproduce like their progenitor.
Chemist Homer Jacobson performed a similar sort of trick using a modified model train set.71 His motorized carriages trundled around a circular track, turning into sidings one by one to couple with others looking for all the world as if they knew exactly what they were doing. With only the aid of a children’s toy, Jacobson had conjured up a vision of self-replicating machines.

Then there were dreamers who were not content with merely demonstrating the principles of machine reproduction. They wanted to tap the endless production potential of clanking replicators. What they envisioned, in essence, were benign versions of Dick’s autofac. One of the first proposals sprang from the imagination of mathematician Edward F. Moore. His ‘Artificial Living Plants’ were solar-powered coastal factories that would extract raw materials from the air, land and sea.72 Following the logic of von Neumann’s kinematic automaton, the plants would be able to duplicate themselves any number of times. But their near-limitless economic value would come from whatever other products they would be designed to manufacture. Moore thought that fresh water would be a good ‘crop’ in the first instance. He envisaged the plants migrating periodically ‘like lemmings’ to some pre-programmed spot where they would be harvested of whatever goods they had made.
‘If the model designed for the seashore proved a success, the next step would be to tackle the harder problems of designing artificial living plants for the ocean surface, for desert regions or for any other locality having much sunlight but not now under cultivation,’ said Moore. ‘Even the unused continent of Antarctica,’ he enthused, ‘might be brought into production.’
Perhaps unnerved by the prospect of turning beaches and pristine tracts of wilderness into smoggy industrial zones, no one stepped forward to fund Moore’s scheme. Still, the idea of getting something for nothing (at least, once the considerable start-up costs are met) appealed to many, and the concept lingered on the fringes of science. Soon, minds receptive to the idea of self-reproducing automata thought of a way to overcome one of the principal objections to Moore’s project. The risk that the Earth might be swamped by machines intent on multiplying themselves endlessly could be entirely mitigated, they conjectured – by sending them into space. In recognition of the fact these types of craft are inspired by the original theory of self-reproducing automata, they are now called von Neumann probes.
Among the first scientists to think about such spacecraft was von Neumann’s IAS colleague Freeman Dyson. In the 1970s, building on Moore’s idea, he imagined sending an automaton to Enceladus, the sixth-largest of Saturn’s moons.73 Having landed on the moon’s icy surface, the automaton churns out ‘miniature solar sailboats’, using only what materials it can garner. One by one, each sailboat is loaded with a chunk of ice and catapulted into space. Buoyed by the pressure of sunlight on their sails, the craft travel slowly to Mars, where they deposit their cargo, eventually depositing enough water to warm the Martian climate and bring rain to the arid planet for the first time in a billion years. A less fantastic proposal was put forward by Robert Freitas, a physicist who also held a degree in law. In 2004, he and computer scientist Ralph Merkle would produce the veritable bible of self-replicating technology, Kinematic Self-Replicating Machines, a definitive survey of all such devices, real or imagined.74 In the summer of 1980, Freitas made a bold contribution to the field himself with a probe designed to land on one of Jupiter’s moons and produce an interstellar starship, dubbed ‘REPRO’, once every 500 years.75 This might seem awkwardly long to impatient Earth-bound mortals, but since REPRO’s ultimate purpose is to explore the galaxy, there was no particular hurry. Freitas estimated that task would take around 10 million years.
The most ambitious and detailed proposal for a space-based replicator was cooked up over ten weeks in a Californian city located in the heart of Silicon Valley. In 1980, at the request of President Jimmy Carter, NASA convened a workshop in Santa Clara on the role of artificial intelligence and automation in future space missions. Eighteen academics were invited to work with NASA staff. By the time the final report was filed, the exercise had cost over US$11 million.
The group quickly settled on four areas that they thought would require cutting-edge computing and robotics, then split into teams to flesh out the technical requirements and goals of each mission. The ideas included an intelligent system of Earth observation satellites, autonomous spacecraft to explore planets outside the Solar System and automated space factories that would mine and refine materials from the Moon and asteroids. The fourth proposal was considered the most far-fetched of all. Led by Richard Laing, the team behind it laid out how a von Neumann-style automaton might colonize the Moon, extraterrestrial planets and, in time, the far reaches of outer space. ‘Replicating factories should be able to achieve a very general manufacturing capability including such products as space probes, planetary landers, and transportable ‘seed’ factories for siting on the surfaces of other worlds,’ they declared in their report. ‘A major benefit of replicating systems is that they will permit extensive exploration and utilization of space without straining Earth’s resources.’76
Laing was another alumnus of Burks’s group. He had arrived at the University of Michigan after dropping out of an English literature degree to work as a technical writer for some of the computer scientists based there. When Burks founded the Logic of Computers Group, Laing was drawn to the heady debates on machine reproduction. He soon joined the group and, after finishing a doctorate, explored the implications of von Neumann’s automata. One of Laing’s most lasting contributions would be his proof that an automaton need not start with a complete description of itself in order to replicate. He showed that a machine that was equipped with the means to inspect itself could produce its own self-description and so reproduce.77
At the NASA-convened workshop in Santa Clara, Laing soon found kindred spirits. As well as Freitas, who had recently outlined his own self-reproducing probe design, Laing was joined by NASA engineer Rodger Cliff and German rocket scientist Georg von Tiesenhausen. Tiesenhausen had worked with Wernher von Braun on the V-2 programme during the Second World War. Brought to the United States, he helped design the Lunar Roving Vehicle for the Apollo moon missions.
The team’s ideas were controversial, and they knew it. To dispel the whiff of crankery surrounding their project, they marshalled every bit of science in their favour. While other teams began their reports by stressing the benefits of their chosen missions, the ‘Self-Replicating Systems’ (SRS) group started defensively, carefully laying out the theoretical case that what they proposed was possible at all. ‘John von Neumann’, they conclude sniffily, ‘and a large number of other researchers in theoretical computer science following him have shown that there are numerous alternative strategies by which a machine system can duplicate itself.’
The SRS team produced two detailed designs for fully self-replicating lunar factories. The first unit is a sprawling manufacturing hub that strip-mines surrounding land to make commercial products or new copies of itself. A central command and control system orchestrates the whole operation. Extracted materials are analysed and processed into industrial feedstock and stored in a materials depot. A parts production plant uses this feedstock to make any and all components the factory needs. These parts are then either transported to a facility to make whatever products the Earth commands or to a universal constructor, which assembles more factories.
A drawback of this scheme is that a whole factory has to be built on the Moon before the automaton can replicate. The team’s second design, a ‘Growing Lunar Manufacturing Facility’ avoids this difficulty by requiring nothing more to start construction than a single 100 ton spherical ‘seed’ craft, packed with robots dedicated to different tasks. Dropped onto the lunar surface, the seed cracks open to release its cargo. Once more, a master computer directs the action. First scouting bots survey the immediate surroundings of the seed to establish where exactly the facility should be built. A provisional solar array is erected to provide power. Five paving robots roll out of the craft and construct solar furnaces to melt lunar soil, casting the molten rock into basalt slabs. The slabs are laid down to form the factory’s foundations, a circular platform 120 metres in diameter. Working in parallel, other robots begin work on a massive roof of solar cells that will eventually cover the entire workspace, supplying the unit with all the power it needs for manufacturing and self-replication. Meanwhile, sectors for chemical processing, fabrication and assembly are set up. Within a year of touchdown, the team predicted, the first self-replicating factory on the Moon will be fully functional, churning out goods and more factories.
Like Alex Ellery many years later, Laing’s team worried about ‘closure’ – could their automaton operate with the materials and energy available? They concluded that the Moon would supply about 90 per cent of the factory’s needs. Unlike Ellery, who is shooting for 100 per cent closure with his hybrid of 3D printer and rover, they accepted that at the outset of the project, the remaining 4–10 per cent would have to be sent from Earth. These ‘vitamin parts’, they said, ‘might include hard-to-manufacture but lightweight items such as microelectronics components, ball bearings, precision instruments and others which may not be cost-effective to produce via automation off-Earth except in the longer term’.
The social and philosophical problems of their project did not escape the team either. They expected their factories to evolve, just like a biological replicator. Left to their own devices in space, would these machines become conscious, and if so, would they necessarily be happy to serve our ends rather than their own? The machines could be taught ‘right’ and ‘wrong’, but as with people, there was no guarantee of good behaviour. This unsettling conclusion led them to ask if humans would always be able switch off the autonomous factories should they pose a threat – the so-called ‘unpluggability problem’. They thought not. ‘At some point the depth of analysis and sophistication of action available to a robot system may exceed the abilities of human minds to defeat it,’ they say. How to prevent such machines from becoming ‘unpluggable’ should be an ‘urgent subject for further research’.
Yet what Laing’s team felt most keenly was the boundless potential of von Neumann’s automata. ‘How will humankind deal with what has been termed, with some justification, “the last machine we need ever build”?’ they asked. Unleashing replicating machines, they said, may have ‘implications on a cosmological scale’.
Humanity could set in motion a chain reaction of organization sweeping across the Universe at near the speed of light. This organized part of the Universe could itself be viewed as a higher level ‘organism.’ Instead of merely following the laws of mechanics and thermodynamics, something unique in our knowledge would occur. The degree of cosmic organization would increase. Life could become commonplace, whereas now it seems quite rare. New rules, the rules of life, would spread far and wide.
It was not to be. When, in 1983, Laing heard rumours that President Ronald Reagan was about to launch a massive new space initiative, he looked forward to the speech with great anticipation. What the president announced instead was the Strategic Defense Initiative – ‘Star Wars’.
The dream has not been forgotten. In 2021, the Initiative for Interstellar Studies, a charity based in London, unveiled an updated design of a von Neumann probe that they say could be built within a decade.78 Ellery’s group is whittling away at the last few percentage points that will get them to 100 per cent closure. The faithful wait for the call from a patron truly prepared to ‘dare mighty things’.

By the 1980s, von Neumann’s name was synonymous with the idea of self-replicating machines. The headiest days of human space exploration were long gone, but a new era of genetic engineering had arrived, and molecular biology was in the ascendant. In 1982, the US Food and Drug Administration approved Genentech’s ‘Humulin’, a version of the hormone insulin produced by bacteria. The first genetically modified plant, an antibiotic-resistant strain of tobacco, was reported the following year.79 Scientists intrigued by the concept of replicators turned their thoughts from the cosmos to a submicroscopic world populated by molecular machines, rather than robots.
The first to articulate this vision was American engineer Eric Drexler, who began using the term ‘nanotechnology’ to describe the new field of molecular manufacturing. ‘When biochemists need complex molecular machines, they still have to borrow them from cells,’ Drexler says in his influential book Engines of Creation. ‘Nevertheless, advanced molecular machines will eventually let them build nanocircuits and nanomachines as easily and directly as engineers now build microcircuits or washing machines.’80
The first nanomachines, Drexler predicts, would be built from proteins, which already perform mechanical tasks in cells. Happily, machines built from these biomolecules would not even need to be assembled. Much like the wooden replicators Penrose designed link up in precise configurations when shaken together, the protein parts of a complex structure like the outer shell of a virus bounce off each other until complementary chemical forces pull them together and make them stick. These soft biological machines will then serve as a stepping stone to second-generation nanomachines made of tougher stuff, such as ceramics, metals and diamond.
Drexler had come across the transcript of a provocative talk entitled ‘There’s Plenty of Room at the Bottom’ given by Richard Feynman in 1959. ‘What would happen’, Feynman asks, ‘if we could arrange the atoms one by one the way we want them?’ Fired up by the idea, which was consistent with his own thinking at the time, Drexler wanted to realize Feynman’s vision. In Engines of Creation, he proposes an ‘assembler’ a few billionths of a metre long that is able to both replicate itself and make other machines, atom by atom. And, to his later regret,81 he warned of ‘gray goo’ – an apocalyptic scenario that follows the accidental release of dangerous replicators from a lab; ‘they could spread like blowing pollen, replicate swiftly, and reduce the biosphere to dust in a matter of days’.82
Some eminent scientists dismissed the whole idea and accused Drexler of scaremongering. ‘There will be no such monster as the self-replicating mechanical nanobot of your dreams,’ Nobel-prize winning chemist Richard Smalley growled at Drexler from the pages of Chemical & Engineering News.83
But in September 2017, researchers at the University of Manchester published details in Nature of a molecule that could be programmed to make one of four different molecules.84 More recently, chemists at the University of Oxford even claim to have made a rudimentary self-replicating assembler.85 Though Drexler now downplays the role of self-replicating nanobots in molecular manufacturing, his speculations look less far-fetched than they once did.
Von Neumann’s theory continued to spread, replicate and evolve much like the self-reproducing machines it describes. ‘Agent-based models’, which try to simulate the interaction of autonomous individuals, grew out of von Neumann’s cellular automaton. Economist Thomas Schelling, no stranger to von Neumann’s work, was one of the first to use the technique. He investigated segregation in cities with nothing more than a chessboard and two sets of coloured counters (let’s say they are either pink or brown) representing people from two distinct groups.86 The resulting ‘game’ resembles a two-dimensional automaton like Conway’s Life.
His most famous experiment begins with equal numbers of pink and brown counters distributed at random across the board. About a quarter of the squares are left empty to allow counters to move around the board. Each set of counters is assumed to have the same fixed preference for neighbours of its own colour. This preference is expressed as a ratio of a counter’s own colour to counters of the opposite colour in surrounding squares. Imagine that no counter is ‘happy’ if fewer than half its neighbours are of the same colour. Unhappy counters move to the nearest empty square that satisfies their preferences. Most squares have eight neighbours, so a pink counter with three or fewer pinks in surrounding squares will move. Pinks in edge squares move if fewer than three out of five neighbours are of like colour. For corner squares, a pink counter is not content unless at least two of three neighbours are pink. Likewise for brown counters.
When Schelling applied these rules, an initially mixed board partitioned quickly into homogeneous neighbourhoods of the same colour.87
Even a relatively mild proclivity for like-coloured neighbours resulted in segregation. Any preference stronger than 1:3 triggered exodus and eventual partition. ‘Surprisingly, the results generated by this analysis do not depend upon each color’s having a preference for living separately,’ noted Schelling. ‘They do not even depend on a preference for being in the majority!’88
Furthermore, once the counters had segregated, the process could not be reversed by softening the bias towards like-coloured companions. A return to more mixed neighbourhoods occurs only when an upper limit is introduced to the fraction of like-coloured neighbours that a counter wants. That is when, for example, counters move if all their neighbours are the same colour.

Schelling had produced two powerful conclusions with a fairly elementary model. First, cities can become segregated along lines of race even if no one minds living in a mixed community. Second, only an active desire for diversity leads to diverse neighbourhoods. Indifference results in segregation.
As agent-based models became more sophisticated, and computers more ubiquitous, the simulations became digital. Robert Axelrod’s tournaments for duelling Prisoner’s Dilemma strategies were an early example. Now, they are used to understand everything from the growth of bacterial colonies and housing markets to tax compliance and voting behaviour.
Perhaps because of its near endless mindboggling implications, von Neumann regarded his automata work as the crowning achievement of his later years. Ulam says the theory of replicating machines was, along with his other contributions to computing, von Neumann’s ‘most permanent, most valuable, most interesting work’.89
Goldstine agrees. ‘It not only linked up his early interest in logic with his later work on neurophysiology and on computers,’ he says, ‘but it had the potential of allowing him to make really profound contributions to all three fields through one apparatus. It will always be a fundamental loss to science that he could not have completed his program in automata theory …’
‘He was never given to bragging or staking out a claim unless it deserved it,’ Goldstine continues. ‘Very possibly he wanted his automata work to stand as a monument to himself, as indeed it does.’90
Over seven decades since von Neumann first lectured on his theory of cellular automata, its possible implications are still being worked out. Plausibly, it could yet give us nanomachines, self-building moon bases and even a theory of everything. Yet while it took just a few years for Turing’s computing machine to be turned from mathematical abstraction to physical reality, the self-replicating machines von Neumann imagined have not yet been made. Or have they?
‘The computer – a new form of life dedicated to pure thought – will be taken care of by its human partners,’ predicted the astronomer Robert Jastrow in 1981, ‘who will minister to its bodily needs with electricity and spare parts. Man will also provide for computer reproduction … We are the reproductive organs of the computer.’91
He was almost right. Forty years after Jastrow wrote those words, there are 2 billion computers in the world. But their numbers have been dwarfed by another more fecund automaton – the smart phone. First surpassing the world’s population in 2014, there are now over 10 billion SIM cards in use worldwide, far exceeding the number of people on the planet.92 Over 1.5 billion smart phones were sold in 2019, and they are multiplying in unprecedented numbers, out-breeding humans by a ratio of at least ten to one. Those billions of SIMs are for now largely being used by human beings. That may soon change. For while we use our devices to chat to each other across the ether, more and more of them have started talking to each other too …
A rich cornucopia of possibilities flowed from von Neumann’s lectures on ‘The General and Logical Theory of Automata’ at the Hixon Symposium on Cerebral Mechanisms in Behaviour in 1948. But von Neumann was interested in more than merely proving the possibility of replicating machines. As suggested by ‘cerebral mechanisms’ in the symposium’s title, von Neumann’s automata theory also served to introduce his ideas about the workings of the brain.
Brains do not reproduce, of course – people do – and the highly cerebral von Neumann did not always carefully distinguish between the two. Still, von Neumann’s automata theory and his musings about the brain both sprang from his recognition of the limits of McCulloch and Pitts’s model neurons. And there is at least one sense in which the brain might be considered to be the product of a self-reproducing automaton. A brain must build itself from the bottom up without a blueprint. The several billion base-pairs-worth of data held by chromosomes inside every human cell are not sufficient to describe the brain (or any complex organ) by themselves. A neuron must interact with other neurons through some set of rules that allow the brain’s incredible organization to grow from simple beginnings in the womb. That makes them in some ways kin to cellular automata, which von Neumann, Wolfram and others have shown can produce great complexity without the help of intricate machinery or a guiding plan. At the logical level, meanwhile, von Neumann and other early computer pioneers saw their machines as primitive electronic nervous systems. Brains. Computers. Reproducing machines. It was a heady intellectual mix. A young Jeremy Bernstein, who heard von Neumann expounding his ideas as an undergraduate at Harvard University, described the talks as ‘the best lectures I have ever heard on anything – like mental champagne’.93
In the audience of von Neumann’s Hixon Symposium lecture was a recent mathematics graduate named John McCarthy. He too was electrified and decided there and then that he would try to develop thinking machines.94 His idea was to produce smart machines by tapping evolution. ‘My idea was to experiment with automata,’ McCarthy says. ‘One automaton interacting with another which would be its environment. You would experiment to see if you could get a smart one.’ McCarthy was proposing to bootstrap his way to machine intelligence by pitting one automaton against another.
McCarthy wrote to von Neumann with the idea, and he liked it. Next year, McCarthy went to Princeton to start a doctorate and met with the great mathematician to discuss the scheme again. ‘Write it up, write it up!’ von Neumann urged. Despite performing a few preliminary experiments, McCarthy never did. But the passion for making machines that think, sparked by von Neumann’s talk, stayed with him. It was McCarthy who later coined the term ‘artificial intelligence’ and, together with Marvin Minsky, founded one of the first labs dedicated to its study at MIT in the late 1950s.
Early in 1955, von Neumann was approached with an invitation to present his thoughts on the subject of computers and brains more fully by delivering the Silliman Memorial Lectures at Yale University the following year. The Silliman lectures usually spanned two weeks; but, prestigious as they were, von Neumann immediately asked if he could deliver them in just one week instead. He was a busy man: with his various research and consulting commitments for American government and military agencies, US Air Force planes were constantly being called in to jet him across the country for some important meeting or other.
But not for much longer. On 9 July 1955, von Neumann collapsed while talking on the telephone to Lewis Strauss, the AEC’s chairman.95 He was diagnosed with bone cancer the next month and was rushed to hospital for emergency surgery. By the end of the year, he was in a wheelchair, and all those important meetings were being cancelled. The one engagement he was determined to fulfil was the Silliman lectures: he worked feverishly to get his thoughts on paper and asked the Silliman committee if he could summarize them in just a day or two. But by March, it was clear that even this would be beyond him. He was admitted to hospital again, taking his manuscript with him in the hope that he might be able to edit his ideas into a form someone else could deliver on his behalf. Even that proved impossible.
Yet he had managed to flesh out his thoughts sufficiently for them to be published as a book the year after his death. In The Computer and the Brain von Neumann systematically compares the powers of the machines he helped to invent with the computation that goes on in the soft machine inside the human skull.96 Brains don’t look so impressive. A neuron can fire perhaps 100 times a second, while the best computers at the time were already able to carry out a million or more operations a second – and a modern laptop is at least a thousand times faster than this. Worse, neurons were billions of times less accurate than computer components: every time a signal is transmitted from one neuron to another, there is a risk that errors are exacerbated.
How, then, do brains far more mundane than von Neumann’s accomplish incredible feats that defeat today’s most sophisticated computers like, for example, making up an amusing pun? The answer is that neurons do not fire one after the other, but do their work simultaneously: they are not serial, like von Neumann architecture computers, but parallel – massively so. It was a lasting insight. The artificial neural networks that power today’s best-performing artificial intelligence systems, like those of Google’s DeepMind, are also a kind of parallel processor: they seem to ‘learn’ in a somewhat similar way to the human brain – altering the various weights of each artificial neuron until they can perform a particular task.
This was the first time anyone had so clearly compared brains and computers. ‘Prior to von Neumann,’ says inventor and futurologist Ray Kurzweil, ‘the fields of computer science and neuroscience were two islands with no bridge between them.’97
Some believe it should have stayed that way. Psychologist Robert Epstein, for example, claims that the popularity of the ‘information processing’ (IP) metaphor – that is, viewing the brain as a kind of computer, as von Neumann suggested – has held back progress in neuroscience. ‘The IP metaphor has had a half-century run, producing few, if any, insights along the way,’ he argues. ‘The time has come to hit the DELETE key.’98 Others point out that promising alternative metaphors have been few and far between.
And the metaphor has proved extraordinarily useful for computer scientists working on neural networks and artificial intelligence – albeit after a series of false starts. As von Neumann was writing his Silliman lectures, psychologist Frank Rosenblatt was improving on the McCulloch-Pitts artificial neuron by making one that was capable of learning. Initial high hopes for this ‘perceptron’ faded; in 1969, Minsky and Seymour Papert published a damning book assessing the computational limitations of simple networks of artificial neurons. Funding dried up in the 1970s – the first ‘AI winter’ – and then renewed optimism in the 1980s gave way to a second AI winter, triggered in part by researchers who argued that progress required feedback from the senses (cameras and microphones) and interactions with the real world (through pressure or temperature sensors, for example). Despite the criticisms, in recent years, artificial intelligence algorithms have started to achieve staggering feats – from beating world champion board-game players to teaching themselves how to program – and these algorithms are often run on neural networks composed of artificial neurons not so different from Rosenblatt’s perceptrons.
Some futurologists are now speculating that a superhuman artificial intelligence could transform human society beyond all recognition. That possibility has become known as the technological ‘singularity’ – and that term was first used by someone who had foreseen the possibility decades earlier: John von Neumann.99
In the eleven months that he was hospitalized, von Neumann received a stream of visitors – family, friends, collaborators and the military men with whom he had spent so much time in the latter years of his life. Strauss recalled ‘the extraordinary picture, of sitting beside the bed of this man … who had been an immigrant, and there surrounding him, were the Secretary of Defense, the Deputy Secretary of Defense, the Secretaries of Air, Army, Navy, and the Chiefs of Staff’.100 He left hospital briefly in a wheelchair to accept the Medal of Freedom from President Eisenhower. ‘I wish I could be around long enough to deserve this honour,’ he told the president. ‘You will be with us for a long time,’ Eisenhower reassured him, ‘we need you.’101

Cancer had come at a particularly cruel time. The truth was that von Neumann had been unhappy at the IAS for several years before his death. ‘Von Neumann, when I was there at Princeton, was under extreme pressure,’ says Benoît Mandelbrot, who had come to the IAS in 1953 at von Neumann’s invitation, ‘from mathematicians, who were despising him for no longer being a mathematician; by the physicists, who were despising him for never having been a real physicist; and by everybody for having brought to Princeton this collection of low-class individuals called “programmers”’.
‘Von Neumann,’ Mandelbrot continues, ‘was simply being shunned. And he was not a man to take it.’102
Von Neumann had explored several offers before settling on a free-ranging ‘professor at large’ position at UCLA, where he had been promised state-of-the-art computing facilities would be established. He and Klári were looking forward to a new life on the West coast but only Klári would ever move there.
Hearing that his friend was sick, Kurt Gödel wrote to von Neumann offering his condolences. ‘With the greatest sorrow I have learned of your illness. The news came to me as quite unexpected,’ he began. ‘I hope and wish for you that your condition will soon improve even more and that the newest medical discoveries, if possible, will lead to a complete recovery.’103
But then Gödel, never very tactful, moves on to more important matters. ‘Since you now, as I hear, are feeling stronger, I would like to allow myself to write you about a mathematical problem, of which your opinion would very much interest me …’ He then launches into the description of a Turing machine, which if ever shown to actually exist, ‘would have consequences of the greatest importance’. Namely, despite Turing’s negative answer to the Entscheidungsproblem, Gödel said, it would imply that the discovery of some mathematical proofs can be automated. It is not known what von Neumann made of Gödel’s problem or if he even saw the letter. Klári was by now answering most correspondence on his behalf. What Gödel was describing is now known as the P versus NP problem and would only be rigorously stated in 1971. Today, it is one of the most important unsolved problems in mathematics.
Marina was by now twenty-one years old and engaged to be married. Bob Whitman held a PhD in English from Harvard and had recently landed a job as an instructor at Princeton. But her father was worried that an early marriage would damage her career. ‘Dear, do not misread your own character. You are very, very talented and then some,’ he warned her. ‘You are God’s own chosen executive, and I am not joking. Besides, you like money … You are “genetically loaded” from both sides, both Mariette and I adore money.’
‘It would be a pity, a misery to see you in petty, straightened circumstances,’ he continued, ‘and worst of all, cut off from using your talents and acting your proper role in life.’104 Von Neumann eventually acquiesced to their plan with graciousness, attending their engagement party in December 1955, though he was too sick to attend the wedding itself the following year. His fears that Marina would be forced to squander her talents proved unfounded. Marina rocketed to success with the full support of her husband.
‘I once asked him,’ says Marina, ‘when he knew he was dying, and was very upset, that “you contemplate with equanimity eliminating millions of people, yet you cannot deal with your own death.” And he said, “That’s entirely different.”’105
Terrified by the prospect of his own imminent death, von Neumann asked to see the hospital’s Catholic priest and returned to the faith he had ignored ever since his family had converted to it decades earlier in Budapest. ‘There probably is a God,’ he had once told his mother. ‘Many things are easier to explain if there is than if there isn’t.’
Nicholas could not bring himself to believe that his brother would ‘turn overnight into a devout Catholic’. The change worried von Neumann’s friends too. Ulam wrote to Strauss declaring himself ‘deeply perturbed about the religious angle as it developed’. Marina says her father was thinking of Pascal’s wager and had always believed that in the face of even a small possibility of suffering eternal damnation the only logical course is to be a believer before the end: ‘My father told me, in so many words, once, that Catholicism was a very rough religion to live in but it was the only one to die in.’106
The cancer metastasized, reaching von Neumann’s brain. He hallucinated in his sleep, babbling in Hungarian. Once or twice, he summoned the soldier guarding him to pass on some urgent piece of advice to the military. The mental faculties of the sharpest mind on the planet ebbed slowly away. Towards the end, says Marina, ‘he asked me to test him on really simple arithmetic problems, like seven plus four, and I did this for a few minutes, and then I couldn’t take it anymore; I left the room in tears.’107
Another frequent visitor to von Neumann’s bedside was Teller. ‘I have come to suspect,’ he said later, ‘that to most people thinking is painful. Some of us are addicted to thinking. Some of us find it a necessity. Johnny enjoyed it. I even have the suspicion that he enjoyed practically nothing else.’
‘When he was dying of cancer, his brain was affected,’ Teller recalled. ‘I think that he suffered from this loss more than I have seen any human to suffer in any other circumstances.’108
Von Neumann died on 8 February 1957. He was buried in Princeton Cemetery on 12 February 1957, in a plot beside his mother, who had died of cancer just the year before, and Charles Dán, Klári’s father.
There was a brief Catholic service. His friends from Los Alamos were still perplexed by his conversion. ‘If Johnny is where he thought he was going,’ joked one, ‘there must be some very interesting conversations going on about now.’
Ulam, who probably understood the breadth of von Neumann’s ideas best, lived to see many of them bloom after their creator was gone. ‘He died so prematurely,’ he reflected many years later, ‘seeing the promised land but hardly entering it.’109
Klári Dán von Neumann married for the fourth and last time in 1958, this time to the American oceanographer and physicist Carl Eckart. She moved to La Jolla but could not, in the end, escape her old ghosts. Her body was found washed up on Windansea Beach on 10 November 1963. She had filled her elegant black cocktail dress with 15 pounds of wet sand and walked into the sea. The coroner’s report notes that, according to her psychiatrist, she found her fourth husband ‘disinterested’ and ‘absorbed in his work’, someone who ‘didn’t want to go out and mix’. They slept in separate rooms at opposite ends of the house.110
‘For the first time in my life I have relaxed and stopped chasing rainbows,’ she wrote on the last page of her unfinished memoirs. The chapter entitled ‘Johnny’ begins, ‘I would like to tell about the man, the strange contradictory and controversial person; childish and good-humoured, sophisticated and savage, brilliantly clever yet with a very limited, almost primitive lack of ability to handle his emotions – an enigma of nature that will have to remain unresolved.’111