Product System Modularization in LCA Towards a Graph Theory Based Optimization for Product Design Alternatives

Abstract

In light of current environmental challenges, industrial companies are increasingly required to reduce their individual environmental impact. As these companies face economic constraints, the reduction of the specific impacts needs to be achieved in the most cost-efficient manner. This is leading to trade-offs between the potential environmental improvements driven by particular measures and the costs of these measures. Due to the inherent complexity of product systems many different measures to alter the products properties exist, leading to a high number of possible combination alternatives in the foreground system and consequently to many different product system set-ups and LCA results. Modular LCAs are an approach to calculate these results by performing separated LCAs for all individual life cycle modules, which afterwards are reconnected again to form the LCA results for all possible module combinations. However, when the LCA result of one of these modules is influenced by interactions with other modules, the consideration of these influences leads to a fast rise in the data demand for a modular LCA. Modelling such an optimization problem via graph theory can be a possible way to address interdependencies between modules while still being able to provide the necessary data demand through a systematic graph design.

1 Introduction

To reduce the human interventions with the ecosphere, political agreements regarding the decrease of environmental pollution or global warming have been passed. The Agreement of Paris by the United Nations is a demonstration of the worldwide understanding for the need to limit the rise of the global mean temperature to well below 2 ℃ compared to the pre-industrial level (United Nations 2015). For commercial organisations with business activities or products related to high greenhouse gas emissions, it therefore becomes necessary to reduce the environmental impact of their products or services. As the companies are competing in an economic-focused market, it becomes more and more reasonable to decrease the specific impacts in these areas of operation, where it is cheapest (Poppe 2001).

Companies that produce goods with a complex life cycle (e.g. long supply chain, diverse mix of materials and/or energy-intense use phase) therefore need to assess a cost minimal configuration of their product over the whole life cycle which reduces their environmental impact to a given limit. This typical life cycle consists of a production phase, a use phase and an end of life phase of the product (Broch 2017).

To optimize this life cycle for a given environmental target, e.g. regarding the emissions of greenhouse gases, different approaches can be possible. One approach could be a single emission reduction measure in one of the three phases or a combination of multiple measures throughout the whole life cycle.

To identify this ideal configuration of the products life cycle, an optimization algorithm is necessary, which identifies this ideal set of measures for a given environmental target. Such an algorithm needs information about the individual potential of greenhouse gas emission reduction and costs of each measure. These input data can e.g. be provided via life cycle costing and an environmental impact analysis based on the ISO Norm 14040.

2 Modularization of Product Systems in LCA

With a growing complexity of the analyzed product, the calculation of an LCA becomes a bigger effort. If the product should be improved regarding the environmental properties, many different alternatives can occur across every phase of the products life cycle. A high diversity of possible measures to reduce the greenhouse gas emissions leads to a high demand of LCA-results, as each possible life cycle, which is the result of a unique combination of measures, needs to be assessed separately (Herrmann et al. 2013).

If a given products life cycle can be altered with exemplary 75 different measures aiming for environmental improvement, which can be combined in any possible way, the LCA demand reaches with more than $3.78*10^{22}$ possible combinations extremely high numbers. The established method of “modular LCA” can help to reduce the calculation effort back to an individual LCA for each of the initial 75 measures. A modular LCA of a product system is based on the concept of dividing the life cycle into clearly separable modules, which are then assessed individually (Jungbluth 2000). The LCAs of the individual modules added up result in the LCA of the whole product system. With a high number of alternative modules (which can be combined in many different ways), the effort to analyze the environmental impact of only the modules is far lower than it would be to evaluate the whole life cycle each time (Cerdas et al. 2018; Steubing et al. 2016).

Figure 1 shows an exemplary product system with six different life cycle stages (A to F) and one to three different modules per stage.

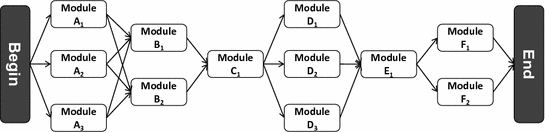
../images/462404_1_En_5_Chapter/462404_1_En_5_Fig1_HTML.gif — Fig. 1
Modular life cycle model

In total, 36 combinations or alternative life cycles are possible for this example and thus possibly 36 different LCA results for the final product. With modular LCAs, this effort can be reduced to twelve LCAs (one for each module), which can then be combined in all possible ways afterwards. Modular LCAs are therefore a smart approach to reduce the amount of necessary LCAs to compare many different life cycle alternatives.

3 Interdependencies Between Measures

A modular LCA approach might lead to wrong results, when the individual LCA of each module is assumed to be static, but actually depends on the modules, it is combined with. When measures are sensitive to the combination with other measures, the initial concept of modular LCAs cannot be applied, as a measure does not have a fixed or static individual LCA result anymore but multiple values, depending on the combination context with other measures. The ongoing calculation with fixed values for interchangeable measures would then lead to incorrect results. This phenomenon can be described as “interdependencies” between measures, respectively modules. (Herrmann et al. 2013)

Referring back to the example of the 75 measures, the calculation of only 75 LCAs and an utilisation of these results in a modular LCA approach cannot be applied, if possible interdependencies shall be considered. If a measure interacts with other measures, than each measure can possibly have an individual value for each possible combination of measures in which it takes part.

On the left side of Fig. 2, an exemplary life cycle with two stages and three modules for stage A (A₁ to A₃) and two modules for stage B (B₁ and B₂) is displayed.

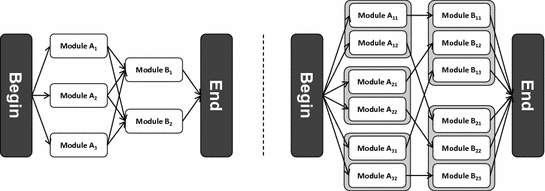
../images/462404_1_En_5_Chapter/462404_1_En_5_Fig2_HTML.gif — Fig. 2
Interdependencies between LCA modules

In total, six alternative life cycles are possible (A₁B₁, A₁B₂, A₂B₁, A₂B₂, A₃B₁, A₃B₂), which can be assessed with only five LCAs (one for each module) via modular LCA. On the right side of Fig. 2 is the same exemplary life cycle depicted. The difference is that possible interdepencies are considered. For example, module A₁ can be combined with either module B₁ or module B₂. If the LCA result of module A₁ depends on the exact combination with a certain module of stage B, than module A₁ can have two different LCA results, one for the combination with module B₁ and one for the combination with module B₂. The same logic applies to the other modules. The total number of possible modules which need to be analyzed with an LCA to apply a modular LCA therefore rises from five to twelve for the same six possible life cycles. Hence, the number of necessary modules surpasses the number of possible life cycles. For larger networks, the difference between the amount of alternative life cycles and the necessary data demand for individual modules growths quickly.

This example shows that the consideration of interdependencies between individual modules within a modular LCA leads to an enormous data demand regarding individual LCAs for each module. This leads to the need for a strategy to reduce the data demand for individual modules below the number of possible life cycles without losing the level of detail, which the consideration of the interdependencies provides for the final results.

4 Data Demand Reduction Strategies

The depiction of the modular LCA and the complexity of interdependencies in the previous sections have been explained via graph theory, as this form of problem representation is very suitable to exemplify the logical and combinatorical relations of life cycle stages. Since the interdependencies between these modules arise due to certain combinations within the chain of life cycle stages, changes in the design of the graph are a helpful approach for the reduction of the data demand. The detailed modifications to these graphs are explained in the following chapter.

The number of existing individual modules considering the possible interdependencies can be calculated with Eq. (1):

$N = y*\left( {n_{1} *n_{2} * \ldots * n_{y} } \right)$

(1)

N = Number of individual Modules

y = Number of life cycle stages

$n_{y}$ = Number of alternatives for each life cycle stage

To reduce the result of this equation, either the number of alternatives per stage or the number of stages needs to be reduced. One effective way of reducing the data demand for a network of a whole life cycle therefore is the principle of forming separated subgraphs, which are afterwards connected again. A subgraph in this context is a graph G’, where the vertices (V’) and edges (E’) are all part of the vertices (V) and edges (E) of the main graph G (Domschke et al. 2015). If it is possible to divide a given graph G into two subgraphs G₁’ and G₂’, the number of possible individual modules reduces quickly, as fewer possible connections appear that lead to the existence of individual modules in G₁’ and G₂’.

The top graph in Fig. 3 would have a total amount of 4374 individual modules [see Eq. (2)], while the two separate subgraphs in the bottom have a data demand for 81 individual modules each [see Eq. (3)].

$4374 = 6*\left( {3*3*3* 3*3*3} \right)$

(2)

$81 = 3*\left( {3*3*3} \right)$

(3)

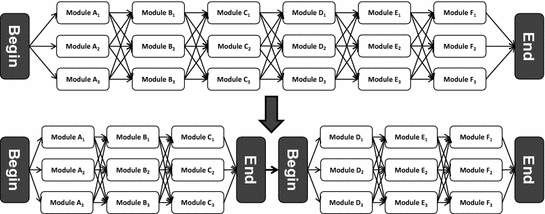
../images/462404_1_En_5_Chapter/462404_1_En_5_Fig3_HTML.gif — Fig. 3
Forming of subgraphs

If every combination of the bottom two graphs are afterwards combined with each other, than both (the top and the bottom) networks offer $3^{6} = 729$ possible combinations or alternative life cycles. While the top network needs 4374 individual modules to provide correct results for the LCAs with interdependencies, it becomes also feasible to calculate these results with only 162 individual modules from the bottom network, if it is possible to split the network in half and calculate separated results. This separation of subgraphs leads to a reduction of −96.3% of necessary individual modules. While the data demand in the top network exceeds the number of possible combinations, the number of individual modules in the bottom network is below that value.

This method is helpful to reduce the necessary LCA data input for a complex life cycle where many, but not all, measures interact. But this approach only helps to reduce the number of individual modules, when multiple subgraphs are combined. Depending on the size of a subgraph, the number of individual modules can also become very large within a single subgraph, which makes it necessary to reduce the amount of data demand not only for the whole life cycle graph, but also within a subgraph itself. The need for the high number of individual modules is based on the possibility of interdependencies between combined measures regarding their specific potential of CO₂-reduction. The source of these emissions, e.g. in the context of a vehicle can be split into the emissions of the production of a measure and the influence of these measures on the emissions during the use phase of the product, if these measures interact.

An additional way of reducing the amount of needed individual modules therefore is to summarize and exclude all the information of interdependencies into one additional stage at the end of the graph. In Fig. 4 on the right side, the graph grows by the stage N, the modules N₁ to N₆ hereby represent the six different interdependency-possibilities of the network. The basic modules A₁ to A₃ and B₁ to B₂ now do not have to be assessed for each interdependency individually, as these basic modules now only store the information of their specific production phase, where the LCA result does not change with further connection of additional measures in this example, while their influence on the use phase are all combined in the newly added stage N. This way, the whole network can provide the result for all combinations including the interdependencies with eleven modules (right side of Fig. 4) instead of twelve modules (left side of Fig. 4). This strategy applied to the two subgraphs in Fig. 3 leads to a number of individual modules of only 36 per subgraph instead of 81, which results in a number of individual modules of 72 for the whole network with a total of 729 possible combinations.

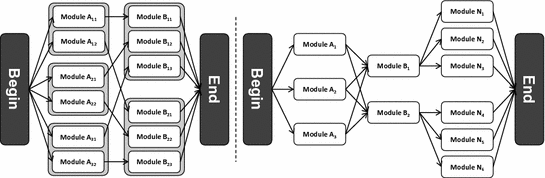
../images/462404_1_En_5_Chapter/462404_1_En_5_Fig4_HTML.gif — Fig. 4
Excluded stage of interdependencies

5 Example

An example for the need of environmental optimization within a complex product can be e.g. found in the automotive industry. With the possibility of adapting different materials, light weight design, powertrains and recycling concepts, many different measures can be applied to a cars life cycle. Interferences between life cycle modules hereby can e.g. be different fuel reduction values for a mass reduction of e.g. 100 kg (possibly by a light weight designed carbody) for different powertrains (Koffler and Rohde-Brandenburger 2010). Transferred to the life cycle graph, at some point the stage “carbody” needs to be combined with the stage “powertrain”. Due to the different fuel reduction values, the emission reduction potential of the same carbody varies for every powertrain it is combined with. These different emission reduction potentials arise due to the different specific emissions of each powertrain for the provision of 1 kWh of energy. While the weight reduction of 100 kg influences the energy demand in kWh for both powertrains in the same amount, the different powertrains save different amounts of CO₂-emissions due to the reduced energy demand in kWh (Rohde Brandenburger 2013). An additional aspect is the recuperation of energy of electric vehicles, which allows heavier vehicles to retrieve more energy during brake-processes (Vetter 2017). This is why the same lightweight designed carbody has a specific CO₂-influence for every powertrain that it is connected with.

A possible use case for subgraphs, e.g. in the context of vehicles is the separation of the whole graph into one subgraph that contains measures that influence the vehicles characteristic properties of the vehicle itself (weight, aerodynamics, powertrain, …) and one subgraph for measures that only influence aspects outside of the vehicles properties, e.g. logistic alternatives. While the LCA-influence of a powertrain e.g. intereferes with measures that influence the energy demand of the vehicle, the transportation of the final vehicle afterwards does not influence the vehicle itself and therefore does not need to be included into the subgraph of the vehicle-properties.

6 Conclusions and Outlook

Interferences between modules within a modular LCA can cause wrong results, making it important to consider interdependencies between measures. When these possible interdependencies should be considered, the number of individual modules rises quickly to a point, where it surpasses the number of possible combinations, making the idea of modular LCA not suitable anymore. To enable the concept of modular LCA again, without losing the level of detail, that the integration of interdependencies between modules provides, two concepts of data demand reduction have been introduced. The first one is the forming of independend subgraphs for groups of modules that only influence separated properties of the product. The second one is the summarizing and excluding of the interdependency scenarios of all modules into a new additional stage, where all interdependencies for each scenario are combined into one module. With these approaches to a systematic graph design, the demand for individual modules can be reduced far below the number of possible combinations.

As the representation of the problem and the reduction of the data demand were both realized using the methods of graph theory, the following optimization of the created input data could also be performed using graph theory based algorithms like shortest path approaches, where the edges represent green house gas emissions. The shortest path through the network therefore would represent the combination of measures with the lowest level of emissions. The advantages of such an algorithm are e.g. the identification of the ideal solution, the simple elimination of technically illogical combinations by cutting out connecting edges and the possibility of expanding the optimization from single vehicles to fleet optimizations by the integration of upper boundaries on the given edges.

Alternative optimization strategies like heuristics or simulation based optimization strategies could also be applied, if the problem size becomes to big for graph theory approaches. The performance of these strategies is yet to be evaluated.

References

Broch, F.: Integration von ökologischen Lebenswegbewertungen in Fahrzeugentwicklungsprozesse, Springer Verlag (AutoUni-Publication Series, Wolfsburg) (2017)Crossref
Cerdas, F., Thiede, S., Herrmann, C.: Integrated computational life cycle engineering—application to the case of electric vehicles, CIRP Ann.–Manuf. Technol. (2018)
Domschke, W., Drexl, A., Klein, R., Scholl, A.: Einführung in Operations Research. Springer Verlag (2015)
Herrmann, I., Hausschild, M., et al.: Enabling optimization in LCA: from “ad hoc” to “structural” LCA approach—based on a biodiesel well-to-wheel case study. Int. J. Life Cycle Assess. Springer Verlag (2013)
Jungbluth, N.: Umweltfolgen des Nahrungsmittelkonsums, Öko-Institut e.V. (2000)
Koffler, C., Rohde-Brandenburger, K.: On the calculation of fuel savings through lightweight design in automotive life cycle assessments. Int. J. Life Cycle Assess. 15(1), Springer Verlag (2010)
Poppe, H.: Indikatorgestützte Umweltbewertung zur Steuerung der Produktentwicklung in der Automobilindustrie, Papierflieger Verlag (CUTEC-Publication Series 53, Clausthal-Zellerfeld) (2001)
Rohde Brandenburger, K.: Was bringen 100 kg Gewichtsreduzierung im Verbrauch?. ATZ. 115(07–08) Springer Verlag (2013)
Steubing, B., Mutel, C., Suter, F., Hellweg, S.: Streamlining scenario analysis and optimization of key choices in value chains using a modular LCA approach. Int. J. Life Cycle Assess. 21(4) Springer Verlag (2016)
United Nations: Paris Agreement, United Nations Framework Convention on Climate Change. (2015)
Vetter, P.: Leichtbau fällt nicht schwer ins Gewicht, Welt am Sonntag Nr. 49, Axel Springer SE (2017)