CHAPTER 13
How Much Diversification?
Portfolio Diversification versus Securities Concentration
Corporate Diversification versus Concentration
The concept of diversification as a hedge against unsystematic risk is a central tenet of efficient portfolio theory (EPT) and is part and parcel of the capital asset pricing model (CAPM) and the more modern arbitrage pricing theory (APT). Unsystematic risk is only a fancy term to describe the risk of loss from trading or holding a security that arises from the market participant’s:
If you are an outside passive minority investor (OPMI) that belongs to the above category of market participant, you better diversify to the fullest extent possible. If you believe in the efficient market hypothesis (EMH) and believe that universal equilibrium pricing exists, then you ought to diversify. The EMH is addressed to those who study securities market prices and have no detailed knowledge about corporations, to non-control OPMIs, and to people who utterly lack price consciousness because they assume that the OPMI market price is an equilibrium price with universal applicability.
Conversely, for market participants following a fundamental finance approach, whether the investor should concentrate or diversify will depend on:
Like the concept of investing, which is best understood when contrasted with the concept of speculation, the concept of diversification can also be better understood when contrasted with the concept of concentration.
PORTFOLIO DIVERSIFICATION VERSUS SECURITIES CONCENTRATION
It is logical where measures of risk are based on the quality of the issuer that portfolios of such securities be diversified, providing added protection to compensate for lack of knowledge about individual securities. In contrast, the investor who, because of know-how or control, has confidence in an equity investment based on price of the issue, and who has a financial position that will allow him to survive the short term, does not need the extra protection that comes from diversification. Such protection comes from a lack of encumbrances upon the investor. He stands to gain most from concentrating his investment in the area where his knowledge (and perhaps control) tips the risk-reward ratio for the particular security very strongly in his favor.
A simple framework that illustrates this point and that also provides a means for calculating the degree of diversification or concentration needed to achieve the maximum growth rate of investment capital over time was developed by John L. Kelly Jr. in 1956.1 Although developed to address a different problem, what is known as the Kelly formula can be used to determine the size of a series of investment commitments relative to available investment capital that will yield the maximum growth rate of capital over time.
The Kelly formula is presented below:
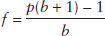
where:
f is the fraction of current capital to commit to a particular investment to maximize compounded returns over time.
p is the probability of making money on the particular investment within an established time period.
b represents the odds or win/loss ratio for the investment.
Since f represents the fraction of available current capital that must be devoted to a particular investment commitment, it is the equivalent of a portfolio weight. A large portfolio weight means a concentrated portfolio since the total number of investments taking up all available capital will be the reciprocal of f. For example, an f of 0.25 would mean that the investor should commit 25 percent of his or her investment capital to that particular investment. An investor following the Kelly rule will have only four such investments in his or her portfolio (i.e., 1/f or 1/0.25).
Let us now use the Kelly formula to illustrate the issues that we have discussed before. We start with an OPMI that believes in the EMH and universal equilibrium pricing, lacks knowledge of the fundamentals of the business, lacks control, is price unconscious, and is likely to have very small odds of making money on any single security selection. We characterize this particular OPMI as having odds of 50.5/49.5 or 1.0202, and an even chance of either picking a winning security or a losing one; that is, p:1/2. Using these two numbers in the Kelly formula yields f = 0.01. Faced with these odds resulting from no skills in business analysis and security selection, this particular OPMI should only commit 1 percent of his or her investment capital to any single security. If the investor were to invest all of his or her capital in similar securities, his or her portfolio should contain 100 securities; that is, a widely diversified portfolio.
Take an investor following the fundamental finance approach, with excellent knowledge about the fundamentals of the businesses he or she invests in, possessing the discipline to only buy securities at prices representing meaningful discounts from readily ascertainable net asset values, but lacking control or access to super-attractive finance. Being price conscious and having knowledge about the business improves this investor’s odds. In this case, the odds on any single security purchase are more likely to be 52/48 or 1.08, and the probability of selecting the winning issuers and securities accurately is p:0.52. Using the Kelly formula with these realistic values yields f = 0.0769 suggesting that the investor should commit almost 8 percent of its investment capital to any individual security so selected. Were the investor to invest all his or her available capital, the portfolio would contain only 13 securities.
Finally, we look at an investor possessing control and access to attractive finance (say, an LBO sponsor) for whom the odds on his or her investments are more likely to be 60/40 or 1.5, and for whom the probability of picking these winning investments is p:0.70 since sponsors are afforded the possibility of conducting extensive due diligence on the companies they invest in. The Kelly formula for the case of a leveraged buyout (LBO) sponsor yields f = 0.5, that is, the sponsor should commit 50 percent of its available capital to any such identified opportunity. Were the LBO sponsor to invest all of its currently available capital it would have two deals in its current portfolio.
We have simply shown that investors wishing to grow their capital over time at high rates should choose their diversification level based on the criteria that we have outlined. These examples serve to remind the reader that diversification is a surrogate, and usually a damn poor surrogate, for knowledge, control and price consciousness.
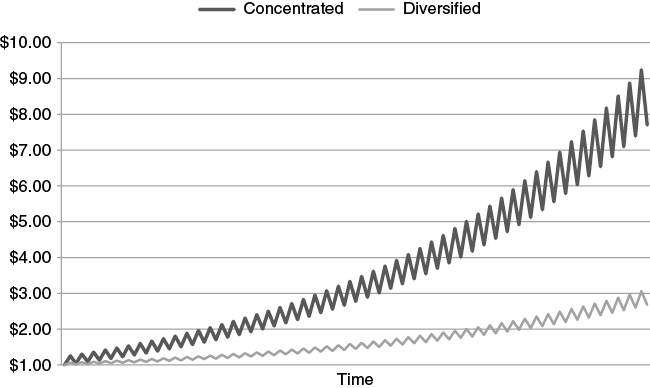
The Kelly formula is also very useful in helping us understand the importance of the right amount of concentration or diversification on both the ultimate performance and the lumpiness or volatility of such performance. One of the arguments used to support the validity of the EMH is that it is impossible to beat market averages consistently, that is, most of the time. We have argued elsewhere that the true test of superior performance is total return over long time periods and not whether a market average is beat consistently. In fact, we can use the Kelly formula to show that the performance of a manager using the right amount of concentration will be superior over the long term but very lumpy and volatile during any specific, relatively short period of time chosen. By the same token, a manager that may be restricted in the amount of concentration used (say because the manager is a registered investment company (RIC) and must abide by strict diversification rules) could significantly underperform relative to what his/her investment approach could yield over long time periods if the right amount of concentration is used. In Figure 13.1 we present the results of an investment operation having a win/loss ratio of 1.5 where the probability p of finding winning investments is ½. Using these assumptions in the Kelly formula yields an f = 0.1667, which would lead to a highly concentrated portfolio of only six investments. The performance of this investment operation shown as the growth of capital over time is labeled “concentrated” on Figure 13.1. We also graph the performance of a portfolio that is built using the same approach to investment selection but over-diversifies four times more than the concentrated portfolio.
Figure 13.1 tells the story. Two facts stand out from this exercise: (1) the performance of the concentrated portfolio is far superior than the one corresponding to the overdiversified one, and (2) the concentrated portfolio performance is quite a bit more volatile than the overdiversified one over any arbitrary time window.
Figure 13.1 Growth in Capital and Performance Lumpiness When Following the Optimal Concentration Rule versus the Diversified Rule
An investment operation can be reduced to the problem of forming a portfolio of investments. The two issues in forming a portfolio are:
In this book we address the first issue. The Kelly framework highlights the substantive importance of the second one. As is almost always the case, conventional wisdom is rather misleading on the topic of diversification. For those investors following a fundamental finance approach to investing, too much diversification can mightily detract from performance. Concentration and lumpiness in performance are to be expected from following the right investment approach. For those OPMIs lacking knowledge, control, and being price unconscious, (i.e. the market participant that EMH and MCT address) substantial amounts of diversification must be used. Specifically, we believe that a common stock portfolio consisting of investments in companies enjoying strong financial positions, priced at a relatively large discounts from readily ascertainable net asset value (NAV), where the market participant has available comprehensive disclosures, should be relatively more concentrated and relatively less diversified. We feel comfortable insofar as at least 50 percent of a common stock portfolio consists of issues issued by companies where: the company enjoys a super strong financial position; the common stock is priced at, at least, a 20 percent discount from readily ascertainable NAV; disclosures are comprehensive; the common stock is traded in well regulated markets, and the prospects appear good that over the next three to seven years, NAV will grow by not less than 10 percent compounded annually after adding dividends.
CORPORATE DIVERSIFICATION VERSUS CONCENTRATION
Corporate diversification can be viewed as a contributory reason for acquiring an equity as well as for not acquiring one. Certain managements in certain situations seem to do extremely well by having a singleness of purpose—that is, by pouring all their resources into one industry. McDonald’s is a good example of a highly successful, primarily single-purpose business. Other companies that have concentrated on one line of endeavor seem to have suffered mightily for having done so. Companies in the cement and steel industries provide examples of businesses that might have fared much better had they diversified. Correspondingly, certain companies have been highly successful because of aggressive diversification into other businesses and industries. Examples include such diverse businesses as Cheung Kong Holdings and Brookfield Asset Management. But attempts at diversification have been anywhere from unsatisfactory to disastrous for such others as Boise Cascade, Beck Industries, Commonwealth United, Litton Industries, and Time Warner.
There is no a priori way for concluding that corporate diversification is per se good or bad. As we discussed in the previous section using the Kelly framework, diversification usually requires a high order of managerial ability, in operations as well as in investing. Many authorities apparently believe that concentration on diversification was a prime cause of the Penn Central bankruptcy. The facts are that the Penn Central management had some degree of success as investors on behalf of the railroad; they apparently were abominable at operating a railroad. The contribution of cash to the railroad operations generated by Penn Central’s investments kept the business alive longer than otherwise would have been the case. The theory that the Penn Central management would have been better railroad operators had they not concentrated so much on investments may have some validity.
SUMMARY
How much diversification should be used in the construction of investment portfolios? It depends. If you believe in the EMH and in universal equilibrium pricing, then you should diversify. For the fundamental finance investor, however, diversification is a damn poor surrogate for knowledge, control, and price consciousness. Fundamental finance investors’ portfolios will tend to be concentrated rather than diversified. We use the Kelly formula to illustrate why this should be the case.
1 John L. Kelly, Jr., “A New Interpretation of Information Rate,” Bell System Technical Journal 35 (1956): 917–926.