A Surplus of Surreal Number Games
Some said ‘John, print it’;
others said, ‘Not so.’
Some said ‘It might do good’;others said, ‘No.’
-JOHN BUNYAN, Apology for His Book
John Horton Conway, the almost legendary mathematician of the University of Cambridge, quotes the above lines at the end of the preface to his book, On Numbers and Games (Academic Press), or ONAG as he and his friends call it. It is hard to imagine a mathematician who would say not so or no. The book is vintage Conway: profound, pathbreaking, disturbing, original, dazzling, witty and splattered with outrageous Carrollian wordplay. Mathematicians from logicians and set theorists to the humblest amateurs will be kept busy for decades rediscovering what Conway has left out or forgotten and exploring the strange new territories opened by his work.
The sketch of Conway included in the book could be titled “John ‘Horned’ (Horton) Conway.” Shown growing out of the top of his head are infinitely regressing, interlocking horns that form, at the limit, what topologists call a “wild” structure; this one is termed the Alexander horned sphere. Although it is equivalent to the simply connected surface of a ball, it bounds a region that is not simply connected. A loop of elastic cord circling the base of a horn cannot be removed from the structure even in an infinity of steps. (A four-horned mechanical puzzle sold as Loony Loop has a nylon loop that can be removed.)
Conway is the inventor of the computer game Life, which I had the honor of introducing in this department in October, 1970, and February, 1971. By carefully choosing a few ridiculously simple transition rules Conway created a cellular automaton structure of extraordinary depth and variety. Now he has done it again. By invoking the simplest possible distinction—a binary division between two sets—and adding a few simple rules, definitions and conventions, he has constructed a rich field of numbers and an equally rich associated structure of two-person games.
The story of how Conway’s numbers are created on successive “days,” starting with the zeroth day, is told in Donald E. Knuth’s novelette Surreal Numbers (Addison-Wesley, 1974). The construction of the numbers is based on one rule: If we are given a left set L and a right set R and no member of L is equal to or greater than any member of R, then there is a number {L | R} that is the “simplest number” (in a sense defined by Conway) in between.
By starting with literally nothing at all (the empty set) on the left and the right, { | }, one obtains a definition of zero. Everything else follows by the technique of plugging newly created numbers back into the left-right arrangement. The expression {0 | 0} is not a number, but {0 | }, with the null set on the right, defines 1, { | 0} defines -1 and so on.
Proceeding inductively, Conway is able to define all integers, all integral fractions, all irrationals, all of Georg Cantor’s transfinite numbers, a set of infinitesimals (they are the reciprocals of Cantor’s numbers, not the infinitesimals of nonstandard analysis) and infinite classes of weird numbers never before seen by man, such as

where ω is omega, Cantor’s first infinite ordinal.
Conway’s games are constructed in a similar but more general way. The fundamental rule is: If L and R are any two sets of games, there is a game {L | R}. Some games correspond to numbers and some do not, but all of them (like the numbers) rest on nothing. “We remind the reader again,” Conway writes, “that since ultimately we are reduced to questions about members of the empty set, no one of our inductions will require a ‘basis.’”
In a “game” in Conway’s system two players, Left and Right, alternate moves. (Left and Right designate players, such as Black and White or Arthur and Bertha, not who goes first or second.) Every game begins with a first position, or state. At this state and at each subsequent state a player has a choice of “options,” or moves. Each choice completely determines the next state. In standard play the first person unable to make a legal move loses. This is a reasonable convention, Conway writes, because “since we normally consider ourselves as losing when we cannot find any good move, we should obviously lose when we cannot find any move at all!” In “misère” play, which is usually much more difficult to analyze, the person who cannot move is the winner. Every game can be diagrammed as a rooted tree, its branches signifying each player's options at each successive state. On Conway’s trees Left’s options go up and to the left, Right’s go up and to the right.
Games may be “impartial,” as in N im, which means that any legal move can be made by the player whose turn it is to move. If a game is not impartial, as in chess (where each player must move only his own pieces), Conway now calls it a partizan game. His net thus catches both an enormous variety of familiar games, from Nim to chess, and an infinity of games never before imagined. Although his theory applies to games with an infinity of states or to games with an infinity of options or to both, he is concerned mainly with games that end after a finite number of moves. “Left and Right,” he explains, “are both busy men, with heavy political responsibilities.”
Conway illustrates the lower levels of his theory with positions taken from a partizan domino-placing game that I discussed briefly in February, 1974, as the game of Crosscram. The board is a rectangular checkerboard of arbitrary size and shape. Players alternately place a domino to cover two adjacent squares. but Left must place his pieces vertically and Right must place his horizontally. The first player who is unable to move loses.
An isolated empty square
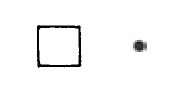
allows no move by either player. “No move allowed” corresponds to the empty set, so that in Conway’s notation this simplest of all games is assigned the value { | } = 0, the simplest of all numbers. Conway calls it Endgame. Its tree diagram, shown at the right of the square, is merely the root node with no branches. Because neither side can move, the second player, regardless of whether he is Left or Right, is the winner. “I courteously offer you the first move in this game,” writes Conway. Since you cannot move, he wins.
A vertical strip of two (or three) cells

offers no move to Right but allows one move for Left. Left’s move leads to a position of value 0, so that the value of this region is {0 | } = 1. It is the simplest of all positive games, and it corresponds to the simplest positive number. Positive games are wins for Left regardless of who starts. The region’s tree diagram is shown at the right above.
A horizontal strip of two (or three) cells

allows one move for Right but no move for Left. The value of the region is { | 0} = -1. It is the simplest of all negative games and corresponds to the simplest negative number. Negative games are wins for Right regardless of who starts.
A vertical strip of four (or five) cells

has a value of 2. Right has no moves. Left can, if he likes, take the two middle cells in order to leave a zero position. But his “best” move is to take two end cells, because that leaves him an additional move. If this region is the entire board, then of course either play wins. But if it is an isolated region in a larger board or in one of many boards in a “compound game,” it may be important to make the move that maximizes the number of additional moves it leaves for the player. For this reason the tree shows only Left’s best line of play. The value of the game is {1,0 | } = {1 | } = 2. A horizontal strip of four cells has a value of -2. If only one player can move in a region and he can fit n of his dominoes into it but no more, then clearly the region has the value +n if the player is Left and -n if the player is Right.
Things get more interesting if both players can move in a region, because then one player may have ways of blocking his opponent. Consider the following region:

Left can place a domino that blocks any move by Right, thus leaving a zero position and winning. Right cannot similarly block Left because Right’s only move leaves a position of value 1. In Conway’s notation the value of this position is {0,-1 | 1}={0 | 1}, an expression that defines 1/2. The position therefore counts as half a move in favor of Left. By turning the L region on its side one finds that the position is {-1 | 0,1} {-1 | 0}= -1/2, or half a move in favor of Right.
More complicated fractions arise in Conway's theory. For example,

has a value of [½ | 1} = 3/4 of a move for Left, since 3/4 is the simplest num- ber between 1/2 and 1, the values of the best options for Left and Right. In a game called partizan Hackenbush (the impartial form of this game was ex- plained in my January 1972 column and is more fully treated in Conway’s book), Conway gives an example of a position in which Left is exactly 5/64 move ahead!
The values of some game positions are not numbers at all. The simplest example is illustrated in Crosscram by this region:

Both Left and Right have opening moves only, so that the first person to play wins regardless of whether he is Left or Right. Since each player can reduce the value to 0, the value of the position is {0 | 0}. This is not a number. Conway symbolizes it with * and calls it “star.” Another example would be a Nim heap containing a single counter. It is the simplest “fuzzy” game. Fuzzy values correspond to positions in which either player can win if he moves first.
The value of a compound game is simply the sum of the values of its component games. This statement applies also to the value of a position in a game in progress that has been divided by play into a set of subgames. For example, the illustration below shows a position in a game of Crosscram played on a standard chessboard. The values of the isolated regions are indicated. The position seems to be well balanced, but the regions have a sum of -1/4, which means that Right is a fourth of a move ahead and therefore can win regardless of who moves next. This outcome would be tedious to decide by drawing a complete tree, but Conway’s theory gives it quickly and automatically.
A Crosscram position that will result in a win for Right

Illustration by Ronald L. Graham/Andrew Christie
A game is not considered “solved” until its outcome (assuming that both players make their best moves) is known (that is, whether the game’s value is zero, positive, negative or fuzzy) and a successful strategy is found for the player who has the win. This stricture applies only to games that must end, but such games may offer infinite options, as in the game Conway calls “My Dad Has More Money than Yours.” Players alternately name a sum of money for just two moves and the highest sum wins. Although the tree, Conway admits, is complicated, the outcome is clearly a second-player win.
Are these not trivial beginnings? Yes, but they provide a secure foundation on which Conway, by plugging newly created games back into his left-right scheme, carefully builds a vast and fantastic edifice. I shall not proceed further with it here; instead I shall describe a few unusual games that Conway analyzes in the light of his theory. In all these games we assume standard play in that the first person who is unable to move loses.
1. Col (named for its inventor, Colin Vout). A map is drawn on brown paper. L has black paint, R has white. They alternately color a region with the proviso that regions sharing a border segment not be the same color. It is useful to regard all regions bordering a white one as being colored white and all regions bordering a black one as being colored black. A region acquiring both colors drops out of the map as being an unpaintable one.
Conway analyzes Col on the map‘s dual graph [see illustration below], defining what he calls “explosive nodes” and marking them with lightning bolts. Of course the game can be played on white paper with pencils of any two colors. Vout has reported that in the set of all topologically distinct connected maps of one region through five regions nine are first-player wins and 21 are second-player wins. The game in general is unsolved.
A five-region map, with its dual graph (color), for playing Col or Snort

Illustration by Ronald L. Graham/Andrew Christie
2. Snort (after Simon Norton). This is the same as Col except that neighboring regions must be the same color. It too is unsolved. Conway suspects it has a richer theory than Col. His most valuable tip: If you can color a region adjacent to every region of your opponent’s color, do so. In addition Conway has discovered some basic theorems that he reports under the heading “A Short Snort Dictionary.”
3. Silver Dollar Game without the Dollar. The board is a horizontal strip of cells extending any length to the right [see illustration below]. Pennies are arbitrarily placed on certain cells, one to a cell, to provide the initial position. Players alternately move a coin to the left to any empty cell. No jumps are allowed. Eventually all the coins jam at the left, and the person who cannot move loses.
The silver-coin game without the silver dollar

The same game with the dollar

Illustration by Ronald L. Graham/Andrew Christie
The game is simply Nim in one of its endless disguises. (I assume that the reader is familiar with Nim and knows how to determine the winning strategy. If not, he can consult any number of books, including Conway’s book or my Scientific American Book of Mathematical Puzzles & Diversions.) Corresponding to the Nim heaps (or rows) of counters are the vacant cells between pennies, starting with the vacancy at the extreme right and including only alternate vacancies. In the illustration the Nim heaps are indicated by brackets and one arrow. The heaps are 3, 4, 0 and 5, so that the game is equivalent to playing Nim with rows of three, four and five counters.
Rational play is exactly as in Nim: Move to reduce the Nim sum of the heaps to 0, a game with a second-player win. The one trivial difference is that here a heap can increase in size. If, however, you have the win and your opponent makes such a move, you immediately restore the heap to its previous size by moving the coin that is just to the right of the heap.
If in the illustrated position it is your move, you are sure to win if you make the move indicated by the curved arrow. If your opponent responds by moving counter A two cells to the left, the move raises the empty heap to 2. Your response is to move B two cells to the left, thus returning the heap to 0.
4. Silver Dollar Game with the Dollar. This is the same as the preceding game except that one of the coins (any one) is a silver dollar and the cell farthest to the left is a money bag. A coin farthest to the left can move into the bag. When the dollar is bagged, the game ends and the next player wins by taking the bag.
This game too is Nim disguised. Count the bag as being empty if the coin at its right is a penny and full if it is the dollar, and play Nim as before. If you have the win, your opponent will be forced to drop the dollar in the bag. If the winner is deemed to be the player who bags the dollar, count the bag as being full if the coin at its right is the coin just to the left of the dollar and count it as being empty otherwise. The position shown corresponds to Nim with heaps of 4, 3, 0 and 2. The first player wins in both versions only if he makes the move indicated by the curved arrow.
5. Rims. The initial position of this pleasant way of playing a variant of Nim consists of two or more groups of spots. The move is to draw a simple closed loop through any positive number of spots in one group. The loop must not cross itself or cross or touch any other loop. A game is shown in the illustration below.
A position in Rims
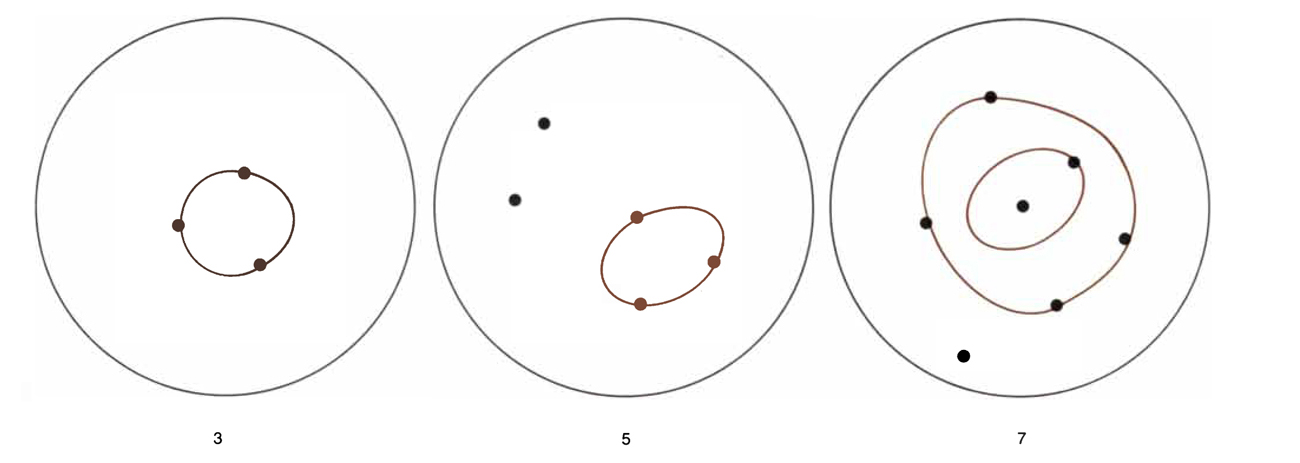
Illustration by Ronald L. Graham/Andrew Christie
Conway shows that Rims is the same as Nim played with the added rule that you are allowed, if you like, to take from the center of a row, leaving two new rows instead of one or more rows. Although the number of heaps can increase, the winning strategy is standard Nim strategy. If each loop is confined to one or two spots, the game is equivalent to the familiar game of Kayles. (See Chapter 16 of my Mathematical Carnival.) Conway calls it Rayles.
6. Prim and Dim. Let me introduce these games by explaining Prime Nim, a simpler game not discussed by Conway. It was first analyzed some 20 years ago by Claude E. Shannon. Prime Nim is played the same way that Nim is except players must diminish heaps only by prime numbers, including 1 as a prime. “The game is actually a bit of a mathematical hoax,” wrote Shannon (in a private communication), “since at first sight it seems to involve deep additive properties of the prime numbers. Actually the only property involved is that all multiples of the first nonprime are nonprime.”
The first nonprime is 4. The strategy therefore is merely to regard each heap as being equal to the remainder when its number is divided by 4 and then to play standard Nim strategy with these modulo-4 numbers. If 1 is not counted as being prime, the strategy is less simple in standard play and is so complicated in misère play that I do not believe it has ever been solved.
Prim, suggested by Allan Tritter, requires that players take from each heap a number prime to the heap’s number. In other words, the two numbers must not be equal or have a common divisor other than 1. Dim requires that a player remove a divisor of n (including 1 and n as divisors) from a heap of size n. Conway gives solutions to both games as well as variants in which taking 1 from a heap of 1 is allowed in Prim and taking n from a heap of n is not allowed in Dim.
7. Cutcake. This is a new partizan game invented by Conway. It is played with a set of rectangular cakes, each scored into unit squares like a waffle. Left’s move is to break a piece of cake into two parts along any horizontal lattice line, Right’s is to break a piece along any vertical line. The game has a surprisingly simple theory.
The illustration below shows a 4 X 7 cake. In Conway’s notation its value is 0, which means it is a second-player win regardless of who goes first. It looks as if the vertical breaker, who has twice as many opening moves as his opponent. would have the advantage, but he does not if he goes first. Assume that the vertical breaker goes first and breaks along the line that is indicated by the arrow. What is the second player’s winning response?
A format for Cutcake, with the first move being a vertical break at the arrow
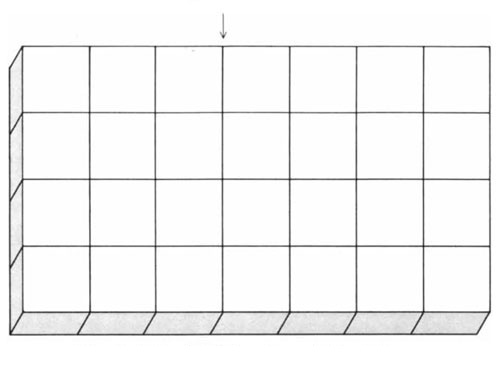
Illustration by Ronald L. Graham/Andrew Christie
I have given only a few examples of Conway’s exotic nomenclature. Games can be short, small, all small, tame, restive, restless, divine, extraverted and introverted. There are ups, downs, remote stars, semistars and superstars. There are atomic weights and sets with such names as On, No, Ug and Oz. Conway has a temperature theory, with thermographs on which hot positions are cooled by pouring cold water on them. He has a Mach principle for the small world: the atomic weight of a short all-small game is at least 1 if and only if the game exceeds the remote stars!
Conway’s theorem 99 conveys some notion of the book’s whimsical flavor. It tells us (I paraphrase to remove a slight error that Conway discovered too late to correct) that any short all-small game of atomic weight zero is dominated by some superstar. Only a feeling of incompleteness, Conway adds, prompts him to give a final theorem. Theorem 100 is: “This is the last theorem in this book.”
--Originally published: Scientific American 235(3);206-211. (September, 1976)