Upon completion of this chapter, you should understand the following:
The restructuring performed by transformation operations of transpose, pivot, and melt.
How to recognize when data is not in tidy form and what transformations and operations should be used to normalize it.
How to use transformations and operations to achieve common presentational goals for a data set or subset.
Perform transformations in pandas:
Transpose,
Pivot and Pivot Table,
Melt.
Use a sequence of pandas operations to achieve normalization and presentational goals.
9.1 Tabular Model Constraints
Recall that constraints are limitations on the organizational structure, the relationships, and the values entailed in a data set. For the tabular model in general, the structural constraints are articulated by the precepts of tidy data, repeated from Sect. 6.1 here:
- 1.
Each column represents exactly one variable of the data set (TidyData1).
- 2.
Each row represents exactly one unique (relational) mapping that maps from a set of givens (the values of the independent variables) to the values of the dependent variables (TidyData2).
- 3.
Exactly one table is used for each set of mappings involving the same independent variables (TidyData3).
For a particular data set, we might, additionally, have data set specific constraints like the following examples:
A column named age must consist of integer values.
A column named income is a categorical variable and must be one of the strings, "high", "middle", or "low".
A column named year must not have any missing values.
If an income column is "low", a salary column must be a float with values less than or equal to 24000.0.
The first three of these are intra-column value constraints, and the last is an inter-column constraint, which, for this structure, says something about a relationship between two variables. These additional constraints might be required for the sound and correct interpretation of the data set for analysis.
When data is created by a provider source, it is often created either without adhering to the structural constraints of tidy data or not necessarily adhering to intra- and inter-column constraints. In the tabular model, there is neither checking nor enforcement to ensure any limitations on the data are met.
In order to provide a check to see if a given data set conformed to these kinds of limitation, there must be some means to specify the limitations themselves. However, in the tabular model, our data arrives in files or through network streams that are almost always in a “record per line” and “fields delimited by a special character” format, conveying the data itself. There is no additional information conveying limitations, as there is with the relational and hierarchical models. So in the tabular model, all constraints are by convention—a common understanding, or by being specified in some outside documentation, or both. Outside documentation describing the form and assumptions of the data is called a data dictionary and often conveys metadata.
Since any creator of data can choose how to take data and put it into a row and column tabular form, the biggest concern is whether or not the data conform to the structural limitations of the model. In other words, we must always be asking the question of whether or not the data violates any of TidyData1, TidyData2, or TidyData3. Any intra- and inter-column constraints are data set specific, and, without additional information, cannot be addressed in a general manner.
In Sect. 6.1, we illustrated, for the topnames data set, four different representations of the same set of data values, all of which violated one or more of the tidy data principles. It may be worth reviewing those examples before continuing on in this chapter. The main observation is this: just because data is organized in rows and columns does not mean that it conforms to the tabular model. Data can be organized in rows and columns in many different ways, and many of those ways violate the tidy data requirements.
Since intra- and inter-column constraints are data set specific and cannot be handled in a general manner, the goal of the current chapter is to better understand the three principles of tidy data, to help recognize when data does not conform to the model, and to give some tools and examples so that, in the eventuality of having data in an un-tidy form, we can transform it into its tidy data equivalent.
In Sect. 9.2, we discuss some advanced operations that allow us to transform one tabular structure into another tabular structure. These, along with the operations of Chaps. 7 and 8, will give us the tools we need in order to work with data in various un-tidy forms and to transform and restructure it. In Sect. 9.3, we present a series of vignettes that illustrate many commonly occurring un-tidy forms and give examples of the normalization process. Finally, in Sect. 9.4, we generalize some of the characteristics seen in the normalization examples and articulate some of the “red flag signs” that can help us to recognize when data is not tidy.
9.1.1 Reading Questions
Give 2–3 reasonable column constraints for the data frame topnames.
Give 2–3 reasonable column constraints for the data frame indicators.
Give an example from a previous time in your life when you have needed to reference information from a data dictionary.
Describe one of the examples of an un-tidy way to display the topnames data set, and explain what specifically makes it un-tidy.
9.1.2 Exercises
The data set ratings.csv has information on several individuals and the ratings they provided for each of two restaurants (called “A” and “B”). Is this data in tidy form? Explain.
Explore the data provided as ratings.csv, and then draw the functional dependency that it should have when in tidy form. Hint: there should be only one independent variable.
The data set restaurants_gender.csv has information on several individuals and the ratings they provided for each of two restaurants. Is this data in tidy form? Explain.
This question concerns popular songs, based on a public domain data set known as billboard:
A portion of this data is hosted on the book web page, and another snippet is visible here:
Is this data in tidy form? Justify your answer.
This question concerns the data set matches.csv hosted on the book web page and keeping data on sports match-ups. Each row is a team, and the columns tell how well a particular team did against each opponent. Does this data conform to the tidy data restrictions? Justify your answer.
This question concerns data from the World Bank about population per country from 2000 to 2018, including the total population, the population growth, the urban population, and the urban population growth, for each country and each year.
- 0.
Read world_bank_pop.csv into a data frame dfwb.
- 1.
Give a reason why dfwb fails to represent TidyData.
Explore the data provided as world_bank_pop.csv, and then draw the functional dependency.
Download the World Health Organization’s “Global Tuberculosis Report” data set as a CSV file from
Look at the CSV file. Is it in tidy data form?
Consider the data set members.csv on the book web page. Please list all steps that would be required to make this data tidy.
9.2 Tabular Transformations
Transformations are the process of converting from one tabular form into another tabular form, while maintaining the information and values represented. We should note that, while these are viewed as complex operations of the tabular data model, they are simply algorithms that are constructed from the more basic operations: selection, projection, iteration, and so forth, which we have already learned. They are well defined and, if we needed to, we could construct these operations for ourselves. But because of their common utility, packages such as pandas in Python, or dplyr in R, have written them for us and allow us to leverage their implementation.
While, in the context of this chapter on constraints, our focus will be on using these transformations to normalize a data set from an un-tidy form, these tools can also be used for some types of analysis. They could also be used when communicating about a data set, manipulating the data into a form for presentation, and allowing us to communicate effectively. Because of this, the discussion in this section will be general, conveying the effect of each transformation, while also highlighting data situations where each transformation should be used.
9.2.1 Transpose
In linear algebra, a transpose is described as reflecting a matrix over its main diagonal. The columns of the matrix become the rows, and the rows become the columns, and an element that was at row i and column j becomes the element at row j and column i. The same transformation can be used to swap the rows and columns of a data frame, in case they are provided incorrectly, with variables as the rows and individuals as the columns.



In pandas, the transpose operates so that the row labels become the column labels and vice versa, so the transpose is almost always used in situations where the row labels are a meaningful index.
9.2.2 Melt
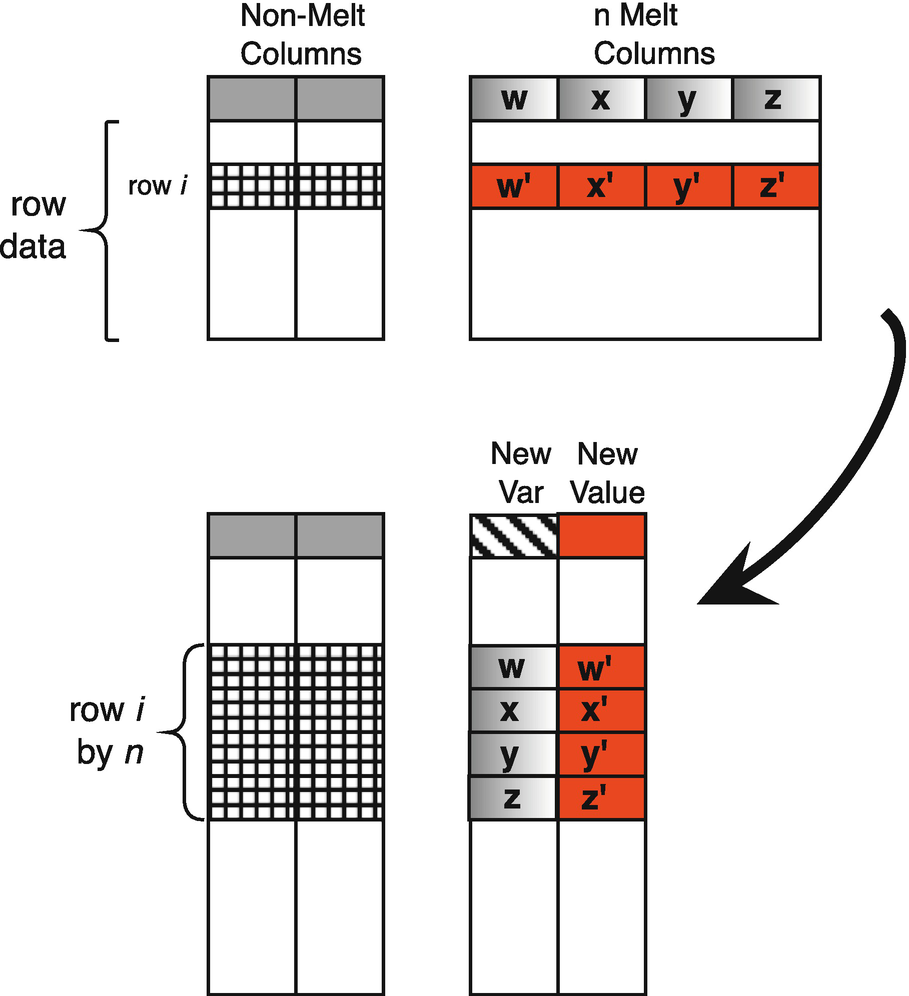
Melt operation

The melt operation takes a subset of the columns, the melt columns, and uses the column labels of the melt columns as table entry values under a single new column, called the new variable. The operation uses the values from the original melt columns to become a single new value column in the transformation. This operation is particularly useful when the names of columns in a data set are, in fact, values in the data set, and we need to create a new column for these values.
Figure 9.1 highlights the transformation of row i in the original data frame, with column labels w, x, y, and z and values in row i of w′,x′, y′, and z′. For example, in our un-tidy topnames data, i could be name, the melt columns could each be a year (e.g., w = 2013, x = 2014, etc.), and the red values could be the top names (e.g., w′ = “Sophia,” x′ = “Emma,” etc.).
In the transformed result, this single row i becomes four rows, corresponding to the original columns (w, x, y, and z) and the values of w′, x′, y′, and z′ are gathered in a single new column. The same transformation is applied to every row, e.g., a row of counts (with one column per year) is reshaped into a column named count with one row per year.
the non-melt column, I, which remains and will repeat its values in the rows of the melted result,
the new variable column, which we name K, whose values come from the column labels in the original, and
the new value column, which we name V, whose values come from the values in the melt columns of the original.
The rows of the result are obtained by expanding, for each row in the original, n rows in the result, where n is the number of melt columns. The n rows will repeat the I value, will use exactly one of the column labels for the K column, and will use a lookup of I and the particular melt column to get the value for V.
We repeat example1 and note the n = 3 columns to be melted:

The values of K are exactly the names of the melted columns. And the values of V are exactly the data values from inside table example1. The table meltresult1 has a default integer row index that we use to help describe the result of the melt operation. Rows 0, 3, and 6 in meltresult1 are transformations of row A in the original table. Note that the entry A.I appears n = 3 times in column I. In row 0, the column 1 from the original has become value 1 under new variable column K, and the value in row A, column 1 of the original, namely A.1, has become the value under column V for row 0. Similarly, row 3 is obtained from row A and column 2 of the original, and row 6 is obtained from row A and column 3 of the original.
allow the function to partition the columns into the melt columns and the non-melt columns,
provide a name for the new variable column, and
provide a name for the new value column.
In the pandas melt( ) method of a DataFrame, the id_vars= named parameter allows us to specify the non-melt column or columns, the value_vars= named parameter allows us to specify the melt columns, the var_name= provides the name for the new variable column, and the value_name= provides the name for the new value column. Since we are partitioning the columns between those to be melted and those not melted, we only need to specify one of id_vars and value_vars, and the operation can determine the other. If we do not specify var_name or value_name, the melt( ) will use very generic defaults of var and value for the new column labels.
Top baby names by year
Sex | 2015 | 2016 | 2017 |
|---|---|---|---|
Female | Emma | Emma | Emma |
Male | Noah | Noah | Liam |
Baby names melted
Sex | Year | Name |
|---|---|---|
Female | 2015 | Emma |
Male | 2015 | Noah |
Female | 2016 | Emma |
Male | 2016 | Noah |
Female | 2017 | Emma |
Male | 2017 | Liam |
In code, the Python variable names_by_year refers to the original data set:

In this case, we specify only the non-melt column of sex as id_vars, and pandas uses the remaining columns for the melt columns. As usual, the values of the non-melt column have been repeated, explaining why we have three rows with “Female” and three with “Male.”
The name of melt for the operation is intended to convey the idea that some of the columns are “melted” and become rows in the result, transforming a wider table into a table with fewer columns, but with more rows. In pandas, this operation is also performed by the stack method, which uses the row label index as the non-melt column and all other columns as the columns to be melted. Other languages, like R, have a gather( ) function to perform the same operation.
When there is more than one column that makes up the non-melt columns, all the values of the non-melt columns are repeated in each of the rows of the result generated from the same row or the source. We show this with the abstract example2, where we have two non-melt columns, I and J:

Again, rows with indices 0, 3, and 6 are the melted result from row A in the original, and all of these have the same values for the non-melt columns, I and J. Note how this introduces the redundancy of having the I as well as J values repeated in the result.
In this section, we have focused on melt( ) , but if a data set and/or developer are skilled at using single- and multi-index with data sets, the stack( ) (and unstack( ) ) can be useful for accomplishing the same goals. Additional information about pandas facilities for transformation/reshaping can be found in their user guide [45] and in the references for melt( ) [41] and stack( ) [44].
9.2.2.1 [Optional] Stack Examples
This optional section presents simple examples of the use of stack( ) to accomplish the same goal as explored with melt( ) .


In this case, the result is one-dimensional—we are left with only one non-index column, and so the result is a Series object, albeit one that has a two-level Index. We have seen this exact kind of data frame in the context of topnames in Sect. 6.3.2. If K consisted of year data (say, 2014, 2015, and 2016), and I consisted of sex data, then A.I might be Male (with the three years as the inner index) and B.I might be Female (again representing three rows, one per year). The values A.1, A.2, etc. would be the applicant numbers for top births by sex and year. The reader who is still confused is encouraged to pause and draw the table we have just described.


9.2.3 Pivot
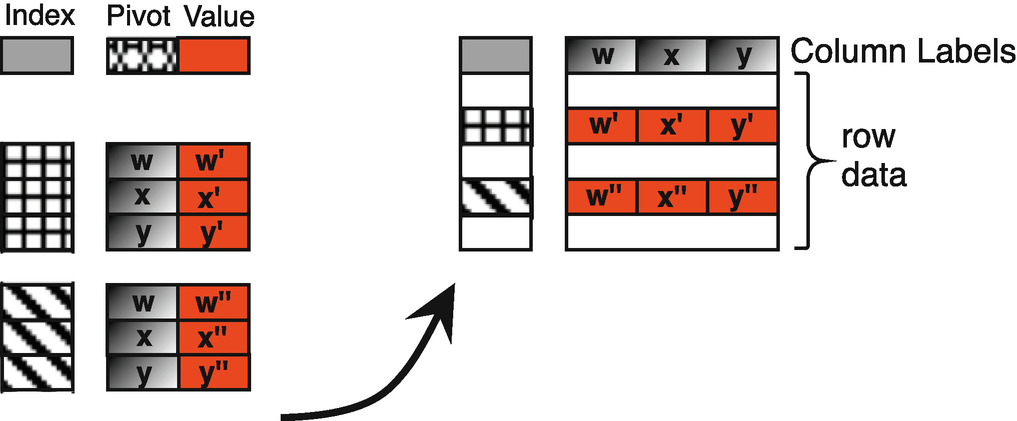
Pivot operation

Shortly, we will show how to make this data tidy using a pivot transformation. First, we describe the pivot transformation in general. In Fig. 9.2 we show, among many possible rows in an original table on the left, two sets of rows that, using matching values in the column annotated as “Index”, will be combined into a single row of the result. In the column annotated as “Pivot,” we see three unique values, x, y, and z that are repeated between each of the two sets of rows (just like pop, gdp, and life). So there are six values in the column annotated as “Value.”1 The values themselves are denoted with single and double prime marks (e.g., because the pop of Canada can be different from the pop of the USA) and must be included in the transformed result.

Furthermore, the values in the resulting table (after the pivot transformation) can be characterized as follows. At the intersection of an “Index” value and one of the values from the “Pivot,” we find the corresponding values from the “Value” column of the source. For example, in the source (ind_to_pivot), the “Value” associated with Canada and life was 82.30, and that is the same value we see after the pivot, in the row indexed by CAN and the column life.

So, in this example, there are six distinct values from column V that we want to represent in the final table, two per each of A, B, and C. For each set of rows to combine, the values in the pivot column (K.1 and K.2) distinguish the rows from each other, and the same pivot values are repeated in each set. There is exactly one column, I, that uniquely identifies the set of rows to collapse. Think of I and K as two independent variables that yield a dependent variable V.
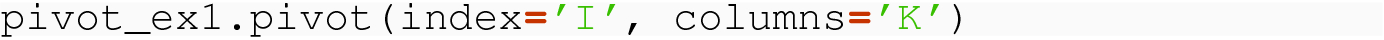
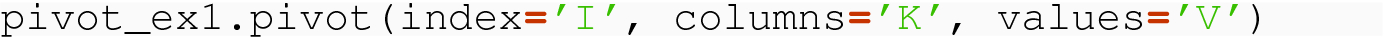
This is, in fact, the exact command we used to convert from ind_to_pivot to ind_corrected:
We will return to an analogous example in Sect. 9.3, where we will also learn how to drop a level of a multi-level index.

Here, the “Index” column is still I, and the pivot column is still K, but now there are two “Value” columns, V1 and V2, each with unique values to be represented in a pivoted result. In this case, beyond the row label index, we expect four columns, with one for each pairing of the pivot column values K.1 and K.2 with the two value columns V1 and V2.
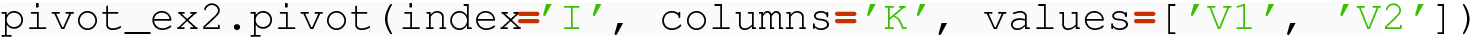
The two-level index of the result of a pivot is helpful here, as it allows a naming for the combinations of value column and pivot column in the result.

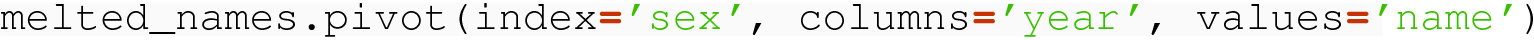



This results in the two-level column label/index and the six desired columns.
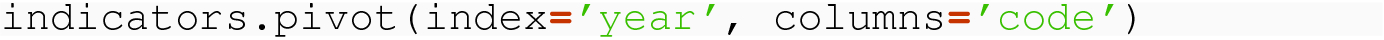
For many data sets, there may not always be exactly the same set of rows in an original to be combined into a single row in the result. Suppose, for example, that the indicators data set has years 2010, 2015, and 2018 for China, just years 2010 and 2015 for India and Great Britain.
The new indicators data frame would look like this:

9.2.3.1 Pivot Table

Here, we would want and expect the result after a pivot to have two rows, one for A and the other for B. But, unlike in the prior examples, we have subsets of rows of the same index with the same value of the pivot variable. For the A rows, there are two rows with a P value of x. But, in the result of a pivot, we would have only one A row and only one x column (for each of V1 and V2). Similarly, there are two B rows with the w pivot.
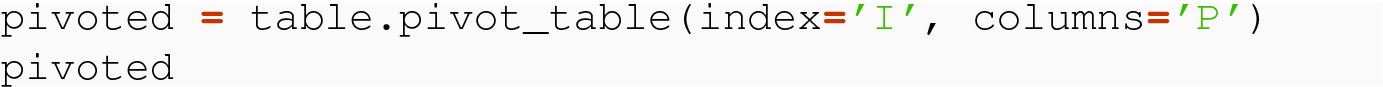
We can see that the value for A and x under V1 is the mean of 10 and 5, and the value for B and w under V2 is the mean of 10.2 and 14.3.

For example, the ( A,x) value of V2 is now 60.5 = 42.5 + 18.


The result builds a multi-level Index in both the row and the column dimensions. We may need to reset the row label/index or perhaps drop the outer level of the result, depending on what further operations are required.
Details for the pivot( ) and pivot_table( ) operations are given the full documentation of the methods of pandas DataFrame objects [42, 43].
9.2.4 Reading Questions
Give a real-world example where you might want to take the transpose. Hint: normally, the rows are in the individuals and columns are traits, so think of a situation where you might want to switch your focus to the traits rather than the individuals.
Does the repetition created by the melt operation mean that the resulting data frame is un-tidy?
Is it possible to do a melt with no id_vars?
The reading gives an example of a data frame that melts into our usual topnames example. Give an example of a data frame that melts into indicators[['code','year','pop']]. Hint: your example should have lots of columns.
Write a sentence describing the number of rows after a melt, based on the number before the melt and the number of melt columns. Does it matter how many non-melt columns there are?
Read the documentation for stack, including how to stack only a subset of the columns. Then, apply stack to the pandas data frame created from this list of lists:
Looking at the Pivot Operation Figure, how can you tell how many new columns and new rows will be present after a pivot operation, based on the columns index, pivot, and value in the original data frame?
In the data frame pivot_ex1, could you have done pivot with other choices of index columns? If so, explain in detail what would have happened.
When doing a pivot, do the arguments index,columns,values have to partition the original columns? Explain.
In the indicators example, does the line
Explain.
Why does it make sense that the default for pivot_table is to take the average of the repeated values?
Carry out the arithmetic to explain why the values in the pivot_table examples are different, i.e., explain where 30.25, 7.5, 6, and 12.25 come from in the first table and where 60.5 and 24.5 come from in the second table.
In the last example of pivot_table, explain what would happen if you chose columns = 'value' instead of columns = 'indicator'.
Consider the original topnames data frame, with year,sex,name, count. Show how to use pivot_table to get a version with sex and year as indices, columns given by name, and with counts as the entries in the data frame.
9.2.5 Exercises
Make the following into a pandas data frame.
Suppose further that we have determined that columns B and D are really values of a variable called X. What transformation/reshaping operation should be used to obtain a tidy version of this data?
At a minimum, what parameter arguments would be needed for this operation to do its job?
Give the column headers of the transformed data set and give at least two rows.
Make the following into a pandas data frame.
If the values one and two from column foo should head columns (so it takes more than one row to interpret a single observation), and the values themselves come from the baz column, what transformation/reshaping operation should be used to obtain a tidy version of this data?
What parameter arguments would be needed for this operation to do its job?
Give the resultant transformed data set, including column headers.
Refer back to ratings.csv and the un-tidy data frame you made in the previous section. Make the data frame tidy, storing your result as ratings_tidy.
Refer back to the restaurants_gender.csv and associated data frame from the previous section. Pivot the restaurants_gender data into a matrix presentation with restaurant down one axis and gender across the other axis. This makes it easy to aggregate female ratings and male ratings. Store the result as rest_mat.
This question concerns the billboard data introduced in the exercises of the previous section. Download this data as a CSV file, read it into a DataFrame, and melt the data frame to make it tidy.
This question concerns the data set matches.csv hosted in the data directory and keeps data on sports match-ups. Each row is a team, and the columns tell how well a particular team did against each opponent.
- 1.
Read matches.csv into a data frame df.
- 2.
Transform the data frame to make it tidy, storing the result as df_tidy. Your data frame should have no NaN values.
This question concerns data from the World Bank about population per country from 2000 to 2018, including the total population, the population growth, the urban population, and the urban population growth, for each country and each year. 0. Read world_bank_pop.csv into a data frame dfwb. 1. Transform the data frame to make it tidy and store the result as dfwb_tidy.
Consider the original topnames data frame, with year,sex,name,count. Show how to use pivot_table to get a version with sex and year as indices, columns given by name, and with counts as the entries in the data frame. Call the result dfPivoted.
With reference to the exercise above, is dfPivoted in tidy data form? Explain your answer.
9.3 Normalization: A Series of Vignettes
With the full suite of transformation operations to help, we are now ready to look at a primary objective of this chapter: given a data set that does not conform to the principles of tidy data, construct a sequence of operations, as an algorithm, to normalize the data into tidy data form.
Because data may be “messy” in an almost infinite variety of ways, the current section is presented as a series of example vignettes, where we show some of the more common violations of tidy data and discuss how our operations from Chaps. 7 and 8 and our transformations from Sect. 9.2 may be employed to resolve the violation(s).
Before any attempt at normalization for a data set, it is of critical importance to understand your data. You must be able to separate what are values from what are the variables. You should be able to argue that variables are different measures. Variables identified as categorical should be assessed on whether they indeed provide different categories that partition observations or whether the “categories” could be variables themselves. Variables should be identified as dependent or independent. Functional dependencies should be written down and examined critically to understand if dependent variables do, in fact, depend on all the independent variables. If one or more dependent variables are determined by a subset of the independent variables, these should give separate functional dependencies and therefore separate tables.
9.3.1 Column Values as Mashup
TidyData1 states that each column must represent exactly one variable. A violation occurs if, in a given data set, either a column is not actually a variable or if a column is in violation because of the exactly one stipulation. Any time the values in a column are some kind of composition of values of more than one variable, a violation has occurred. A composition might mean a mashup, or it could be the result of a column that is a combination of two other columns, or even an aggregation of multiple columns.
9.3.1.1 Example: Code and Country Mashup

At an abstract level, we need to introduce new columns that have, parsed out, the variable values from the current country column and then replace that column with the two new columns. We write our solution as an algorithm.
- 1.
If necessary, reset the index to allow manipulation of country as a column.
- 2.
Define two functions that, given a value of country, yield the code part and the country part.
- 3.
Apply the function to get a code to the current country column, yielding a codes vector.
- 4.
Apply the function to get a country to the current country column, yielding a countries vector.
- 5.
Drop the current country column.
- 6.
Add codes as a column.
- 7.
Add countries as a column
- 8.
If needed, set index to be the new code column.
- 9.
If needed, change the order by projecting columns in the desired order.
The corresponding code to realize this algorithm is as follows:

In the final version of working, we see the normalized data set. In this example, we could also have made country the index and had code as a dependent variable.
9.3.1.2 Example: Year and Month Mashup
Metropolis tourism
Date | Visitors | Rooms | Occupancy | Revenue |
|---|---|---|---|---|
Jan-2015 | 508800 | 28693 | 0.857 | 26124000 |
Feb-2015 | 450500 | 27866 | 0.656 | 25618000 |
Mar-2015 | 783900 | 27717 | 0.940 | 27317000 |
Apr-2015 | 545100 | 27566 | 0.887 | 23254000 |
May-2015 | 602100 | 27656 | 0.891 | 20700000 |
- 1.
When dates are strings, even a simple sort operation, which occurs as a lexicographic ordering of the string characters involved, can yield unexpected results. In this case, a sort would put Apr-2017 as the first entry. Similar problems can occur even if numeric months and days are used, depending on the ordering.
- 2.
When data is in a time series over multiple months and years, analysis can often want to GroupBy the years of the data set, to characterize year over year information, or to GroupBy the months of the data set, to characterize monthly or seasonal trends.
To make time series encoded as composite strings tidy and normalize a data set, we have two choices. First, if a package supports it, we could make use of a DateTime object type. These objects are designed to abstract the nature of years, months, days, hours, minutes, seconds into a single object that can be sorted and, in packages like pandas, can be used in a GroupBy which specifies the frequency (like year or month) of the group. Second, we can use the approach employed above, splitting the string into its component types and replacing the composite column with the individual columns.
9.3.2 One Relational Mapping per Row
TidyData2 states that each row represents exactly one mapping from the values of the independent variables to the values of the dependent variables. This means that if, for a representation, more than one row is employed to give the value of dependent variables for the same independent variable, the data is not in tidy form. In the next two examples, we will look at variations of having multiple rows used to represent a single relational mapping.
9.3.2.1 Example: One Value Column and One Index Column
Indicator data
Code | Indicator | Value |
|---|---|---|
CHN | Pop | 1386.40 |
CHN | Gdp | 12143.49 |
CHN | Exports | 2280.09 |
GBR | Pop | 66.06 |
GBR | Gdp | 2637.87 |
GBR | Exports | 441.11 |
IND | Pop | 1338.66 |
IND | Gdp | 2652.55 |
IND | Exports | 296.21 |



This yields the desired tidy form of the data.
It is worth noting that, when TidyData2 was violated by having more than one row per mapping, TidyData1 was also violated: neither indicator nor value in the original data frame satisfied the condition of a column representing exactly one variable.
9.3.2.2 Example: One Value Column and Two Index Columns
Indicator data
Year | Code | Indicator | Value |
|---|---|---|---|
2015 | CHN | Pop | 1371.22 |
2015 | CHN | Gdp | 11015.54 |
2015 | GBR | Pop | 65.13 |
2015 | GBR | Gdp | 2896.42 |
2015 | IND | Pop | 1310.15 |
2015 | IND | Gdp | 2103.59 |
2017 | CHN | Pop | 1386.40 |
2017 | CHN | Gdp | 12143.49 |
2017 | GBR | Pop | 66.06 |
2017 | GBR | Gdp | 2637.87 |
2017 | IND | Pop | 1338.66 |
2017 | IND | Gdp | 2652.55 |



9.3.3 Columns as Values and Mashups
Another frequent violation of TidyData1 occurs when the column labels represent values of a variable instead of a single variable of the data set. Sometimes this is easy to see, like when the column labels are, in fact, numeric values,2 but sometimes it is less obvious, like when the column name incorporates a variable name along with a value in a mashup as the column name. The next two examples look at variations of this scenario.
9.3.3.1 Example: Single Variable with Multiple Years

Population by year
Code | pop2014 | pop2015 | pop2016 | pop2017 |
|---|---|---|---|---|
CHN | 1364.27 | 1371.22 | 1378.66 | 1386.40 |
GBR | 64.61 | 65.13 | 65.60 | 66.06 |
IND | 1295.60 | 1310.15 | 1324.51 | 1338.66 |
USA | 318.39 | 320.74 | 323.07 | 325.15 |
To normalize this data, we need to start with a melt of the table using all the “popXXXX” columns as the melt columns. The value column of the result will have collected all the values from the original table, as desired. But the “New Var” in the result will still have the mashup of the string "pop" composed with the value of the year, so this will need to be resolved to obtain the integer year value. We write our solution as an algorithm.
- 1.
If necessary, reset the index to allow the use of the code index as a column.
- 2.
Melt the data frame, so that all columns except the code column transform into rows, where the value in the column becomes the pop column, and the previous column name becomes a value in a column named colname.
- 3.
Define a function that, given a value of colname yields the year value.
- 4.
Apply the function to the colname column and assign to the data frame as a column named year.
- 5.
Perform the cleanup of dropping the colname column and setting the index based on two independent variables (year and code); if desired, change the row order so that the index shows grouping in more friendly presentation.
With the original data from Table 9.6 as a data frame referred to by pop_columns, this algorithm translates into the following code and yields the normalized result named tidy:

An equivalent tidy representation could swap the levels of the row Index, and possibly perform a sort_index, if we desired code as the outer index and year as the inner index.
9.3.3.2 Example: Multiple Variables with Multiple Years
Population and GDP by year
pop2015 | pop2016 | pop2017 | gdp2015 | gdp2016 | gdp2017 | |
|---|---|---|---|---|---|---|
CHN | 1371.22 | 1378.66 | 1386.40 | 11015.54 | 11137.95 | 12143.49 |
GBR | 65.13 | 65.60 | 66.06 | 2896.42 | 2659.24 | 2637.87 |
IND | 1310.15 | 1324.51 | 1338.66 | 2103.59 | 2290.43 | 2652.55 |
USA | 320.74 | 323.07 | 325.15 | 18219.30 | 18707.19 | 19485.39 |

Like in the last example, we clearly need to start with a melt, which will transform the data set into a frame with columns for code, as the index, ind_year for the new variable column, and value for the value column. Also, like the previous example, the values in the ind_year column will be strings composed of indicator and year. But now, we will have strings like both 'pop2015' and 'gdp2015'. So now when we separate, we will get two columns, one for the indicator part and the other for the year part.


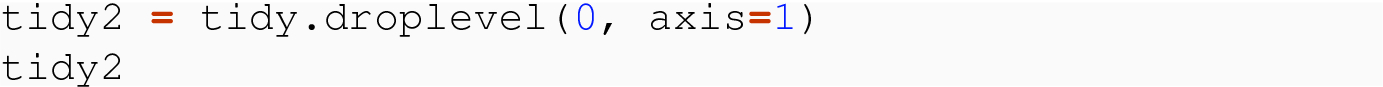
For this example, the original data set, as a data frame, could have been normalized in a couple of other ways than what was presented here.
First, we could have taken the original data frame and, using two different column projections, created a data frame with all the population data and another data frame with all the GDP data. Each of these could have been transformed into a partially tidy data set, with population or GDP indexed by code and year. Then, using the table combination techniques of Sect. 8.3, these partial data sets could be combined into a tidy whole.
A second alternative would involve the use of a two-level Index in the column dimension. If we transformed the data frame, through manipulation of the column Index, so that it had one level of the indicator and the other level of the year, then the pandas unstack( ) method, which generically is really transforming column Index levels into row Index levels, could be used to unstack just the year level. This is a more advanced topic specific to pandas, so we have chosen to omit it.
9.3.4 Exactly One Table per Logical Mapping
Up to now, the examples of messy data we have looked at have all involved TidyData1 and/or TidyData2. The other constraint of this model is TidyData3, which requires that exactly one table be used for a set of mappings (i.e., rows) involving the same combination of independent variables. To better understand this, it helps to think in terms of functional dependencies, where the combination of independent variables is specified by the left-hand side of the relationship.





9.3.4.1 Example: Variable Values as Two Tables
Top female baby names
Year | Name | Count |
|---|---|---|
2018 | Emma | 18688 |
2017 | Emma | 19800 |
2016 | Emma | 19496 |
2015 | Emma | 20455 |
2014 | Emma | 20936 |
2013 | Sophia | 21223 |
Top male baby names
Year | Name | Count |
|---|---|---|
2018 | Liam | 19837 |
2017 | Liam | 18798 |
2016 | Noah | 19117 |
2015 | Noah | 19635 |
2014 | Noah | 19305 |
2013 | Noah | 18257 |



9.3.4.2 Example: Separate Logical Mappings in a Single Table


Combined table
Year | Code | Country | Land | Pop | Gdp |
|---|---|---|---|---|---|
2000 | CHN | China | 9388210 | 1262.64 | 1211.35 |
2000 | IND | India | 2973190 | 1056.58 | 468.39 |
2000 | USA | United States | 9147420 | 282.16 | 10252.35 |
2017 | CHN | China | 9388210 | 1386.40 | 12143.49 |
2017 | IND | India | 2973190 | 1338.66 | 2652.55 |
2017 | USA | United States | 9147420 | 325.15 | 19485.39 |


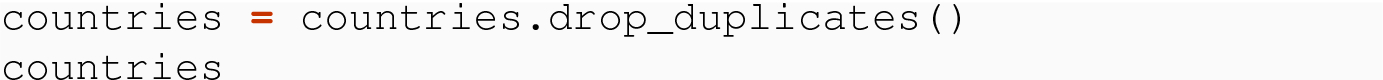
The resulting two tables of countries and indicators are now a tidy data set. We will explore these tools further in the exercises at the end of the chapter.
9.3.5 Reading Questions
In the country example, explain the 3 and 5 that appear in the lambda expression. Illustrate with an example.
Give an example of a way to report dates numerically, but where sorting gives a result different from chronological order.
Give an example of a real-world seasonal trend you might want to study by grouping data by month.
In the un-tidy example of indicators (with three rows for each mapping from a country to its indicators), explain why it is a bad idea to have a single column with three types of separate measures. Rather than speaking in generalities, give a specific example of something that could easily go wrong in such a representation.
Often in scientific inquiry, it is valuable to think about the units of various quantities, e.g., distance being measured in miles. Please write a sentence about how the consideration of units can be useful in determining if a given column satisfies TidyData1.
Consider the example of Population by Year, where normalization resulted in an index of ['year','code']. If the index had been set as ['code','year'] instead, what would the result after sorting look like?
In the example Population and GDP by Year, the data was normalized with a melt followed by a pivot, and alternatives were given after. Could you have normalized it by pivoting first and then doing a melt? Why or why not?
In the Top Baby Names example, what is the difference between pd.concat( [topfemale, topmale], axis=0) and pd.concat( [top male, topfemale], axis=0) ?
In the countries example (with pop,gdp,country,land), is any information lost with the projections
countries = mixed_table[['code', 'country', 'land']] indicators = mixed_table[['code', 'pop', 'gdp']]?
Describe the relationship between countries, indicators, and mixed_table using the language of joins.
How do you think the drop_duplicates( ) command is implemented?
9.4 Recognizing Messy Data
This section attempts to arm the reader with some tools for recognizing violations of one or more of the structural constraints of tidy data (i.e., TidyData1, TidyData2, and TidyData3). We frame these as red flags—characteristics of the structure and the values of a given data set that may indicate a violation. Even to employ these red flags and to truly assess whether or not a given data set is in tidy data form, we must start by understanding the data, as emphasized at the start of Sect. 9.3.
9.4.1 Focus on Each Column as Exactly One Variable (TidyData1)
The following is a sequence of questions we must ask ourselves.
If a table has columns whose value is derived by other columns, e.g., GDP per capita.
If a table has columns where the column labels incorporate multiple parts. The examples in the chapter include cases where there are mashups of a variable name and the value of another variable
If a table has column labels that are values of a variable.
Column labels that are the values of years, months, or days.
Column labels that are the various categories of a single categorical variable; we could imagine topnames with a column for Female and another column for Male.
In a table with a single independent variable, the values of the independent variable are the column labels; consider the country codes in indicators that could be structured as the column labels or the names of patients in a treatment data set.
If the values in a column can be seen as a mashup, possibly using a hyphen (-) or slash (/) or comma (,) to divide parts of the mashup.
If we have dates with multiple parts (year, month, and day) as strings in a single column. Note that a DateTime object in a column is allowed, as it allows proper sorting and GroupBy in the various dimensions of the time series (by year, month, and day of month).
If it makes sense and we are inclined to aggregate values in more than one column for a single aggregate value, then this could indicate that multiple columns are, in fact, values for a single variable.
If it does not make sense to aggregate in a column. This is particularly clear if the units of the values are different, but like units can still exhibit this red flag. Consider the open, close, high, and low stock price in a table of stocks. Taking an average of these values makes no sense, and so a single column of stock prices and another column of high/low/open/close would violate tidy data.
Another way to see this red flag is if we are treating as categorical something that does not give a partitioning and are really independent measures.
If it is not treating as a variable something that gives a categorical partitioning of the data (e.g., Male/Female).
9.4.2 Focus on Each Row Giving Exactly One Mapping (TidyData2)
The following is a sequence of questions we must ask ourselves.
If it makes sense to aggregate across a row, it may mean that the values are somehow compatible and could be values of the same variable, instead of a given row having values of different variables. This could be a subset of the values in a row, as opposed to the full row.
In this case, the row labels would be the names of variables.
If we can write down the functional dependencies and if we can see that a group of rows is needed to capture one mapping instance.
If the name of a dependent variable is a value in a single column. Our “indicator” meta-variable with “values” of 'pop', 'gdp', 'cell', and 'life' is an example where it would take multiple rows to capture a single logical mapping.
If the name of a column is too generic, like “value” or “variable.” This red flag often occurs at the same time as the previous point.
The use of missing data (or some other encoding) to mean that there is not a value for this variable in this row because it is not applicable.
Data rows that are dependent on other rows, like rows that are aggregations for a subset of the rows.
9.4.3 Focus on Each Table Representing One Data Set (TidyData3)
The following is a sequence of questions we must ask ourselves.
If there are multiple tables and the names of the tables are values of a categorical variable, like we had with a Female and a Male table for the topnames data set.
If there are multiple tables and the names of the tables name different dependent variables, particularly if they are dependent on the same independent variable. For instance, the indicators data set might have one table for population and another for GDP, with both being dependent on the independent variables of the year and country code. In this case, if we write down the functional dependencies, the different tables would have the same left-hand side and differ in the right hand sides.
If, when we understand the data and write down the functional dependencies, there are different functional dependencies with one having a subset of the variables on the left-hand side of another. Our example in the book had code, year -> pop,gdp but code->country, land.
If there is repeated data and, upon examination, the redundant data is because, in a row (instance mapping), the repeated data is dependent on less than the full set of independent variables.
9.4.4 Reading Questions
The first red flag for TidyData1 states “If a table has columns whose value is derived by other columns.” Does this description always lead to a violation of TidyData1? Illustrate with examples. This question hinges on how you interpret “derived,” so please be clear in what this term means.
Give an example, different from any in the text, of a table where the column labels incorporate multiple parts.
Give an example, different from any in the text, of a table where we might be inclined to aggregate values in more than one column for a single aggregate value.
Give an example, different from any in the text, of a table with a numerical column that it does not make sense to aggregate, e.g., because it contains values in different units. Your example should involve “treating as categorical something that does not give a partitioning and are really independent values.”
The last red flag listed for TidyData1 says “Not treating as a variable something that gives a categorical partitioning of the data (e.g., Male/Female).” Suppose you had a data set containing salary data for individuals of different hair colors. What would it look like to represent this data set in an un-tidy way, leading to this red flag? What would it look like to represent this data in a tidy way?
Give an example, different from any in the text, of a table where it makes sense to aggregate across a row, and give a specific TidyData assumption your example fails to satisfy.
Give an example, different from any in the text, of a table where a group of rows is needed to capture one mapping instance of the functional dependency.
Give an example, different from any in the text, of a table where the name of a dependent variable is a value in a single column.
Give an example, different from any in the text, of a table where missing data is used to mean that a variable is not applicable to a given row.
Referring to the language of the TidyData assumptions, why is it a violation to have “Data rows that are dependent on other rows, like rows that are aggregations for a subset of the rows”?
Give an example, different from any in the text, of a table where “there is repeated data and, upon examination, the redundant data is because, in a row (instance mapping), the repeated data is dependent on less than the full set of independent variables.”
9.4.5 Exercises
The data set members.csv has a mashup column containing both first and last names. Download this data from the book web page, read it into a data frame, and correct this mashup column.
The data set members.csv has a date column. Correct this as shown in the reading, by splitting it into three columns.
Now correct the date column in members.csv by creating a column of DateTime types.
The data set members.csv has another mashup column. Find it and correct it.
Read us_rent_income.csv from the book web page into a data frame, and then look at the data. Is it in tidy data form? Explain your answer. Note: this data set contains estimated income and rent in each state, as well as the margin of error for each of these quantities. This data came from the US Census.
Explore the data provided as us_rent_income.csv, and then draw the functional dependency.
Read us_rent_income.csv into a data frame (with “GEOID” as the index), and then transform as needed to make it tidy. Store the result as df_rent.
For each of the next four exercises, assess the provided data against our Tabular-Tidy data model constraints. If the data conforms, explain. If the data does not conform, explain why and describe the transformation(s) needed to bring the data set into conformance. Be clear about the columns that would be in the resultant data set.
Below is some (fake) data about the connection between religion and salary. This was inspired by real research done by the Pew Research Center.
Religion | Under 20K | 20–40K | 40K–75K | Over 75K |
|---|---|---|---|---|
Agnostic | 62 | 140 | 173 | 132 |
Buddhist | 49 | 68 | 84 | 61 |
Catholic | 1025 | 1432 | 1328 | 1113 |
Protestant | 1413 | 2024 | 1661 | 1476 |
Jewish | 39 | 50 | 39 | 91 |
Is it tidy? Assess.
Below is (fake) weather data, giving the minimum and maximum temperature recorded at each station on each day.
Date | Element | Station | Value |
|---|---|---|---|
01/01/2016 | tempmin | TX1051 | 15.1 |
01/01/2016 | tempmax | TX1051 | 26.9 |
01/01/2016 | tempmin | TX1052 | 14.8 |
01/01/2016 | tempmax | TX1052 | 27.5 |
01/02/2016 | tempmin | TX1051 | 13.9 |
01/02/2016 | tempmax | TX1051 | 26.4 |
01/02/2016 | tempmin | TX1052 | 14.6 |
01/02/2016 | tempmax | TX1052 | 30.7 |
Is it tidy? Assess.
The following is public transit weekday passenger counts, in thousands.
****
Mode | 2007–01 | 2007–02 | 2007–03 | 2007–04 | 2007–05 | 2007–06 |
|---|---|---|---|---|---|---|
Boat | 4 | 3.6 | 40 | 4.3 | 4.9 | 5.8 |
Bus | 335.81 | 338.65 | 339.86 | 352.16 | 354.37 | 350.54 |
Commuter Rail | 142.2 | 138.5 | 137.7 | 139.5 | 139 | 143 |
Heavy Rail | 435.29 | 448.71 | 458.58 | 472.21 | 474.57 | 477.32 |
Light Rail | 227.231 | 240.22 | 241.44 | 255.57 | 248.62 | 246.10 |
Is it tidy? Assess.
Here is some (fake) stock price data by date.
Date | Apple Stock Price | Yahoo Stock Price | Google Stock Price |
|---|---|---|---|
2010-04-01 | 177.25 | 179.10 | 178.62 |
2010-04-02 | 176.11 | 175.39 | 175.84 |
Is it tidy? Assess.
Similarly to the above, another way that stock data is commonly presented is with one row per company and one column per month. Would that form be tidy? If not, what transformations would be needed to fix it? Justify your answer.
Explore the data from the previous exercise, and then draw the functional dependency. Note: this data came from a survey of individuals about their religion and their income.
Read the data from the previous exercise into a data frame, and then transform as needed to make it tidy.
Download the World Health Organization’s “Global Tuberculosis Report” data set as a CSV file from
Then, wrangle this data into a tidy data frame. Hint: you will need to study the data dictionary carefully.