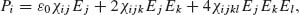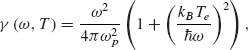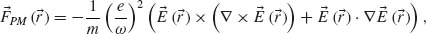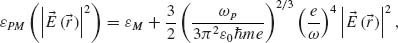2
Nonlinear Effects in Plasmonic Systems
2.1 INTRODUCTION
Nonlinear photonics celebrated its formal 50th anniversary in 2011, following the first experiment of second harmonic generation by Franken et al. in 1961 [1]. It was always the backbone in the evolution of modern optics, yielding exciting discoveries and understanding of fundamental optical phenomena and also serving as a source for a large variety of applications. In optics, nonlinear interactions are relatively weak, such that in many cases the induced polarization vector is treated perturbatively as a power series in the electrical field and serves as a source term in the Maxwell wave equations. However, non-perturbative nonlinear optics at extremely intense excitation is a field of interest today, for example, for high harmonic generation [2], laser-induced fusion [3], and material processing [4]. The quantum nature of light may give rise to a handful of nonlinear phenomena, where quantized vacuum fluctuations initiate nonlinear interactions—one of the most known examples is the spontaneous parametric down conversion (SPDC), where pump light is being dissected into a pair of actual photons that were not present in the system primary to the interaction. At the same year mentioned above (1961), the paper by W. H. Louisell, A. Yariv and A. E. Siegman on quantum fluctuations of parametric processes [5] is considered as the founding year of the quantum nonlinear optics as well.
The integration between nonlinear optics and the very fast evolving field of plasmonics (metal-optics) is of special interest and is the subject of this chapter. This interest stems from the following reasons: metal nonlinearities—metal exhibits both bound electrons nonlinearities (similar to other optical media) and free carrier (plasma) hydrodynamic-like nonlinearities; surface nonlinearities—plasmonics always occurs on metal–dielectric interfaces, thus interface nonlinearities, spatial symmetry breaking, and related phenomena are highly important; field enhancement—one of the merits of plasmonic structures, either in localized or in propagation forms, is substantial field concentration and enhancement, which makes optical nonlinearities much more accessible and applicable; multipolar—for example, electric quadrupole or magnetic dipole interactions can be designed by properly shaping the plasmonic structures and these higher order interactions are intrinsically nonlinear (and nonlocal); subwavelength-scale nonlinear waves—the ability to generate nonlinear optical features such as spatial solitons at the nanoscale, below the wavelength of light; non-phase-matched parametric processes—plasmonic nanostructures are sometimes effective ultra small cavities (slow-light devices), which are replacing the very cumbersome phase-matching configurations of nonlinear conversion schemes.
The very well known historical example of plasmonic-enhanced nonlinearity (although the term plasmonics was not yet coined) is surface-enhanced Raman scattering (SERS), taking place on the interface of rough noble metal, and was shown to enhance the magnitude of the scattering by 14 orders of magnitude compared to the unassisted phenomenon [6]. In the last decade or so, with the explosion in plasmonics research, many related optical nonlinearities were studied, demonstrated, and proposed for applications, for example, for active plasmonic circuitry (the latter is discussed in a different chapter of this book).
In this chapter we discuss some of the nonlinear phenomena closely related to the interplay of light with metallic objects, generally termed nonlinear plasmonics.
The electromagnetic wave equation in its general form is given by
(2.1)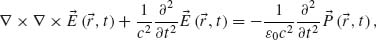 
where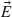 
(
, t) is the electrical field vector, c the speed of light in vacuum, ε0 the vacuum permittivity, and 
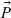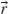(, t) a general polarization term, reflecting the medium response to the incident electromagnetic wave. (, t) encapsulates all the required material information, such as linear and nonlinear dispersive responses. The inclusion of spatial dispersion may be further introduced by more advanced techniques [7] and will not be discussed here in much detail. The polarization term may be decomposed in a series of electrical field, and in the frequency domain it is given by [8, 9]
where subscripts denote vector components at certain directions and χ s are susceptibility tensors of appropriate rank. Enhancement of nonlinearity, as reflected from Equation 2.2, may be gained by manipulation of the intrinsic material susceptibilities or the enhancement of electrical fields. While quantum engineering of internal structures may be performed [10, 11], here we emphasize the contributions of the so-called local field enhancement and fast spatial fields variations, where plasmonics is one of the most promising approaches.
The chapter is organized as follows: In Section 2.2 we discuss physical mechanisms, responsible for nonlinearities in metal structures, emphasizing the difference between local and nonlocal nonlinearities, although they are intermix when the predominant effects are occurring near interfaces. In Section 2.3 we present nonlinear surface plasmon polariton (SPP) propagation, when the nonlinearity is either stemming from the metal or enhanced by the metallic waveguide structure. Nonlinear modes, plasmon solitons, and nonlinear waveguide devices are discussed. In Section 2.4 we introduce nonlinearities enhanced by local surface plasmons within or in the vicinity of nanoparticles and nanoantennas. Sometimes the actual source of nonlinearity is not completely defined under such highly localized enhanced fields, since the largest field and field gradients are occurring exactly at the metal–dielectric interfaces and the nonlinear polarizability can be in either of both the media.
2.2 METALLIC NONLINEARITIES—BASIC EFFECTS AND MODELS
A unified analytical model for metal nonlinearities at the extended optical regime (300–2000 nm) is still missing. The main theoretical challenge is to extract clear information from the complex solid-state structure of metallic objects, surfaces, and surrounding environment in order to isolate the main contributors to certain nonlinear effects. Moreover, nowadays experimental data from different sources are not always consistent mainly because of the large dependence of the mechanisms on the exact quality of the sample and sample surfaces. In general terms, nonlinearities of metal structures originate from two families of physical effects; the first includes bulk point contributions, related to the saturations of interband optical transitions [12], and carriers heating contribution [13, 14]. These types of nonlinear response are exhibited at frequencies exceeding the interband energy gap occurring at the visible spectral range for most of the noble metals. The second family of nonlinearities is attributed to the nonlinear dynamics of the free carriers' plasma, which may be exhibited at any frequency, even below the interband transition. The detailed discussion of metal nonlinearity deserves a book of its own, and here we only briefly elucidate the different characteristics of the two families of nonlinearity by two examples (Sections 2.1 and 2.2) and then discuss their combined effects as a source for parametric process (Section 2.3). Finally, we look into material damage induced by extreme light intensity, which limits the field of metal nonlinear optics and conversely serves as an important mechanism in metal processing (Section 2.4).
2.2.1 Local Nonlinearity—Transients by Carrier Heating
Metal nonlinearity based on collective carriers heating is predominantly observed in short pulse experiments and was employed in pump probe experiments to extract the fast dynamics of collective nonradiative relaxation processes in electron plasma.
Generally, femtosecond (fs) pulses are used for generation of nonequilibrium excitations of the metal electrons via interband transitions (e.g., pulses with ∼400 nm central frequency for Au). The carriers' dynamics may be described by the so-called two-temperature model, where electrons and lattice are assumed to be in internal equilibrium but not in mutual equilibrium ([15] and references therein). In the frame of this model the nonequilibrium electron distribution, created by an fs laser pulse, is thermalized via very fast electron–electron scattering processes, taking place on the scale of hundreds of fs, and subsequently creates a modified Fermi–Dirac electron distribution of “hot” carriers. Electron–phonon scatterings are much slower processes, taking place on the timescale of tens of picoseconds, and they equalize temperatures of the lattice and electrons. Most of the interesting phenomena occur in the window between these two characteristic timescales. The effect is predominantly local because nonlocal mechanisms such as diffusion are much slower compared to the electron–electron thermalization process.
The modified electron distribution yields a broadening of the localized plasmon resonances, modifying the related absorption coefficient. The linear behavior of a sample is recovered after few electron–phonon scattering events. Modification of absorption in metal nanoparticles 10 and 100 nm in size was studied as the function of fs laser excitation intensity [16]. Figure 2.1 shows the recovery dynamics of the absorbance. The simple model attributes the broadening to the temperature dependence of the electrons scattering rate. The Drude approximation with temperature-dependent damping of dielectric permittivity of a bulk metal εM (ω, T) is given by
(2.3)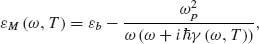 
where εb is the background permittivity, which holds all the information on the interband transitions, ωp the plasma frequency of conduction electron gas, and γ (ω, T) the scattering rate. In the frame of the simple model ([17 and references therein) this term is given by
where kB is the Boltzmann constant and Te the electron gas temperature. The quality factor of the plasmonic resonance is roughly the ratio between the real and imaginary parts of the material permittivity and it is reduced with the increase in the temperature, as may be seen from Equation 2.4.
FIGURE 2.1 Independence of the electron–phonon and phonon–phonon relaxation times on the composition of gold and mixed gold–silver nanoparticles. The transient absorption spectra of 15 nm spherical gold nanoparticles after excitation at 400 nm with 100 fs laser pulses recorded at different delay times is shown. Also shown is the steady-state UV–vis absorption spectrum of the colloidal gold solution. The inset shows the decay of the transient bleach when the particles are monitored at the bleach maximum at 520 nm. Fitting of the decay curve gives electron–phonon and phonon–phonon relaxation times of 3.1 and 90 ps, respectively. (From Reference 16.)
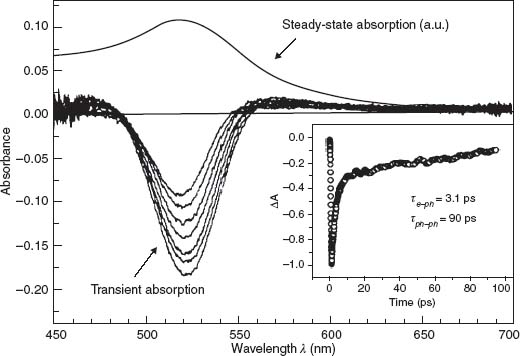
This intensity-dependent (pump) transient absorption (probe) may be enhanced by orders of magnitude, using metamaterial composition, based on nanorod arrays, and further more by nonlocal effects due to the fine features of such structures, as will be discussed in Section 2.4 in connection to parametric processes. The collective coherent mode of the structure overlaps with many nanorods, enhancing the effect and resulting in much faster collective response. Moreover, the steep modal dispersion of this collective excitation together with fast refractive index changes, initiated by the pump, provides much more flexibility and sensitivity for the modulation of the transmitted signal. Appropriate designs may provide a route to ultrafast, low-power all-optical information processing in the deep subwavelength scale [17].
2.2.2 Plasma Nonlinearity—The Ponderomotive Force
Nonlinearity of noble metals may originate from pure hydrodynamics of the free carrier plasma due to nonlocal effects and will also be viable at frequencies lower than those related to the interband transitions. The nonlocal effects of collective interactions of charged particles make the dielectric permittivity to be average-intensity dependent. Such nonlinearity originates from the ponderomotive force (
PM()) [18], repelling charged carriers from regions of high field intensities and thus effectively diluting locally the electron plasma in the conduction band within the high field intensity regions:
where e and m are the electron charge and mass, respectively, ω is the beam central frequency, and 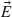(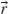) is the local electrical field amplitude. The conservative ponderomotive force may be recast into a potential that is subsequently added to the Fermi energy and results in effective change in electron concentration within the conduction band. The inclusion of fermion statistics in this hydrodynamic approach is required for metals, since the Boltzmann distribution typically used in plasma physics is inapplicable for metals, where the Fermi level is situated deep in the conduction band. The intensity-dependent (according to the shifted Fermi level) concentration of the charged carriers gives rise to nonlocal Kerr-like nonlinear electrical permittivity with a highly dispersive coefficient [19]:
where εM is the linear part of the metal–dielectric constant and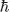 
the Planck's constant. This nonlinear Kerr coefficient is highly dispersive (∼ 1/ω4) and for the telecom wavelength of 1.5 μm is on the order of 10−18 (m2/V2)—comparable with that of typical nonlinear glasses. Detailed book chapter on the dynamical effects in metal plasma may be found in Reference 20.
A number of experimental studies present third-order nonlinearity with susceptibility of the same order of magnitude as predicted by the ponderomotive model. Four-wave mixing (FWM) experiments estimate χ(3) = 0.2 × 10−18 (m2/V2) at λ = 633 nm [21], which is two orders of magnitude larger than values reported for highly nonlinear crystals, for example, LiNbO3.
2.2.3 Parametric Process in Metals
Parametric optical processes in metals will result from both local interband-based nonlinearity and plasma-based nonlinearity and in most cases from their combinations. Second-order interactions require broken spatial symmetry, resulting from either the quantum confining potential or macroscopic (but still subwavelength) geometric features, as may be shown from general considerations of symmetry and time reversal. Thus the second-order susceptibility χ(2) cannot be exhibited by crystals with inversion symmetry and very poorly by amorphous/polycrystalline materials, which are the typical form of both bulk metals and substrates used conventionally in plasmonics. However, the required conditions may be simply fulfilled by geometrical violation of reflection symmetry, such as at abrupt distinct boundaries. Since plasmonics relies on the existence of such interfaces and the surface plasmons reside on them, “efficient” second-harmonic-related phenomena are expected to occur.
In early studies of metal second-order processes by Bloembergen et al. [22] and Jha [23], the conduction band response was modeled in terms of Sommerfeld free electrons, with an extension to a set of basic hydrodynamic equations for free plasma. It is important to note that the mere inclusion of Lorentz magnetic force makes these equations to be inherently nonlinear, coupling charge velocity with overall magnetic field—each of these quantities oscillates with the fundamental frequency and hence generates a source for frequency doubling. The presence of magnetic field violates the time-reversal conditions and results in the so-called magnetic dipole contribution to nonlinearity. Additional source for nonlinear polarization originates from large gradients of electrical field (inherent in plasmonics) that yield multipole contributions. This formalism describes the bulk properties of conduction carriers and does not include the contribution of “surface states” occurring in the region between the nominal interfaces to a depth of few Fermi wavelengths into the metal (a few nanometers for noble metals), where the carrier dynamics is modified. The hydrodynamic formalism was further extended by Sipe et al. ([24] and references therein along with citing articles) and the shortened version of nonlinear polarizability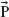 
(2ω) may be written as [25]
where β, γ, and δ' are parameters related to the magnetic dipole and electric quadrupole effects and may be estimated from specific material properties or alternatively measured. A comprehensive theoretical model, taking into account both bound and free-electron contribution to the linear response and nonlinear terms due to free electrons, was developed in Reference 26 and includes six terms, collapsing to Equation 2.7 with certain assumptions on material losses.
Experimental studies of SHG on reflection from flat metal mirrors were first reported in Reference 27. Advanced experimental techniques used in Reference 25 show that the surface contribution predominates the bulk; however, both should be taken into account for proper modeling.
Magnetic dipole interactions are relatively small at the high frequencies of the optical regime. However, their contribution to the SHG may be probed by creation of artificial materials (metamaterials) with significant magnetic responses at the optical frequencies. Arrays of split-ring resonators were shown to enhance the nonlinear phenomena at frequencies near the resonance of the artificial magnetic dipoles [28].
Another consequence of second-order nonlinearity is the photon drag effect, resulting from the zero frequency term of the nonlinear polarizability (related to what is known as optical rectification). The hydrodynamic theory of the effect is developed in Reference 29, the experimental demonstration was first performed for Germanium sample [30], while the plasmonic version was demonstrated in Reference 31 for Kretschmann geometry of SPP excitation and periodic dielectric grating on the metal surface [32]. The extreme nanoplasmonic confinement may also lead to giant photon drag effect and may result in the generation of THz source terms [33].
Theories for higher harmonic generation (third and above) on flat metal surfaces, based on Sommerfeld free-electron models, with subsequent solution of Schrödinger equation in the Kramers–Henneberger accelerating frame were developed [34] and are in good agreement with experimental data [35]. Coherence properties of higher harmonics were studied and it was shown that while the second harmonic is partially coherent, at higher harmonics incoherent emission is dominant [36]—meaning that the predominant effect that we are observing at “higher harmonic generation” is metal luminescence excited by multiphoton absorption. The reason is seemingly because of the very fast electron scattering, causing the loss of coherence of the carriers during the pump pulse duration. Since the efficiencies of second and third harmonics have different power dependence on the excitation, at high-enough intensities third-order process may overcome the second order. In the experimental observation of Pappadogiannis et al. [37] a 4 μm thick polycrystalline gold surface was exposed to 290 fs laser pulses. The duration of the pulses is shorter than the electron–phonon relaxation time, but larger than carrier–carrier scattering time, meaning that electrons are self-thermalized to an equilibrium temperature of thousands of Kelvin. Under these conditions the efficiency of the third harmonic process overcomes the second harmonic at 11 GW/cm2 pump laser intensity.
The first observation of the third harmonic generation from individual colloidal gold nanoparticles was demonstrated in Reference 38. Pump laser at 1500 nm generated a 500 nm signal, in the vicinity of a localized plasmon resonance. The third harmonic signal intensity was shown to be proportional to the square of the particles' surface area.
2.2.4 Metal Damage and Ablation
Nonlinear experiments are typically performed with high-intensity lasers, operating at short pulsed regime to increase peak powers. Thus potential optical damage in nonlinear plasmonic experiments is an important limitation. One of the most pronounced bottlenecks is surface roughness increasing with downscale of noble metal experimental samples, which may cause undesired local field enhancements and effectively magnify the incident field by order of magnitudes, acting as primary sources of electromagnetic damage. The term “laser ablation” is sometimes associated with this type of damage, when materials are evaporated from host surfaces. Different models of laser ablation exist; among them are thermal and photochemical; we refer the readers to a couple of review papers on the subject—References 39 and 40. Briefly, there are four key mechanisms that may lead to the optical damage: linear absorption, resulting in heating of electrons and lattice; avalanche breakdown, where accelerated free electrons cause cascaded ionization; multiphoton ionization; and direct field ionization, initiated by very short energetic pulses [8].
In an experimental study [41], the damage of gold and nickel thin films induced by fs laser pulses was investigated by light-scattering measurements. Film thickness was found to be a key parameter for the measured thresholds. The main mechanism, involved in the process, is the carrier diffusion, occurring in the first picoseconds and strongly depends on electron motilities and phonon scattering cross sections. In the regime of long (ns) light pulses the energy dissipation and transport is defined by the heat diffusion in the lattice. In both regimes the melting is predicted to begin at the surface.
The damage thresholds, as the function of film thickness, are depicted in Figure 2.2.
FIGURE 2.2 Film thickness dependence of the absorbed laser fluence at the damage threshold extrapolated to the single shot value for Au (open circles) and Ni (filled circles). The inset shows a magnification of the thin film range. The solid lines are calculated using the two-temperature model. (From Reference 41.)
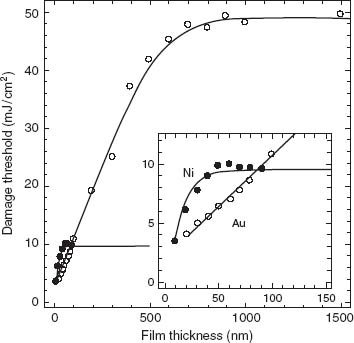
For extra smooth surfaces the main damage mechanism is seemingly the creation of electron plasma in the air above the surface; for example, for a 4 μm thick polycrystalline gold surface, exposed to 290 fs laser pulses, plasma creation was observed at an excitation intensity of 120 GW/cm2 [32]. The temperature of metal surfaces was analytically estimated by the solution of electromagnetic diffraction problem together with heat-transfer equations, distinguishing between different timescales and particle sizes [42].
Laser ablation may also be employed for metal processing, for example, hole drilling on metal surface. Pronko et al. [43] drilled 300 nm diameter holes in a 600 nm film of silver evaporated onto a glass substrate, using Ti:sapphire laser, producing 200 fs pulses with an overall energy of 40 nJ.
2.3 NONLINEAR PROPAGATION OF SURFACE PLASMON POLARITONS
Nonlinear phenomena in general planar and waveguiding structures were extensively studied and we refer the readers to a book chapter in Reference 44, where comprehensive studies of nonlinear waveguide structures are presented. Nonlinear phenomena may lead to contra-intuitive and unexpected results, such as TE surface wave over single interfaces, prohibited in the linear regime for nonmagnetic materials. In this section we discuss some nonlinear phenomena of propagating SPPs, where the nonlinearity stems either from the metal or from the dielectric constituents of the plasmonic waveguide structures.
2.3.1 Nonlinear SPP Modes
The propagation of SPP is modified by third-order nonlinearity even in the most basic SPP-supporting structure: the single metal–dielectric interface [19]. Specifically, SPP nonlinear modes are supported by metal–air interface at wavelengths longer than those related to the interband transition; thus the major nonlinearity stems from the ponderomotive forces within the free carrier plasma (Section 2.2.2). An intuitive explanation of this nonlinear effect is related to the electron depletion in the high-intensity regions that are located just at the metal–air boundary. The linear modal effective index of SPP is given by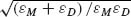 
, where εM and εD are the dielectric permittivities of metal and dielectric medium half-spaces. As a result from the carriers' depletion, the negative metal–dielectric constant near the interface becomes less negative, thus approaching the critical value of εM = −εD, which is the cutoff value for propagating SPP. At light intensity, corresponding to this critical value, the intensity-induced modal reshaping results in equal, but opposite, power flow in the metal and dielectric. The corresponding intensity-dependent nonlinear dispersion relations may be solved analytically without resolving the exact modal shape. The set of coupled nonlinear algebraic equations may be solved for the mode propagation constant β:
(2.8)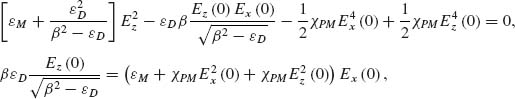 
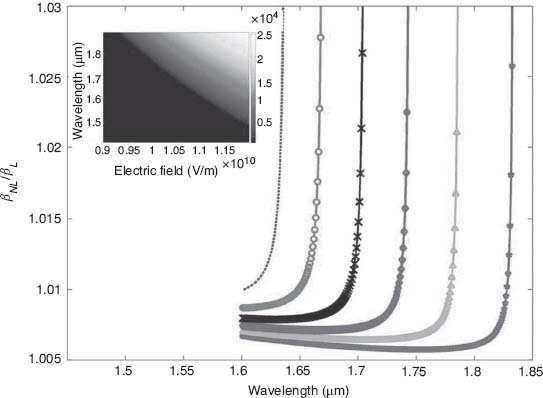
where Ex (0) and Ez (0) are the x (perpendicular to the surface) and z (the direction of the propagation) components of the electrical field phasor amplitude at the interface, εM and εD the linear permittivities of the metal and dielectric substrate, respectively, and χPM the nonlinear ponderomotive susceptibility, defined in Equation 2.6. Solutions of the above equations for different field intensities on the surface are represented in Figure 2.3 [19] showing clearly the intensity-dependent cutoff wavelengths for the nonlinear modes:
FIGURE 2.3 Nonlinear dispersion relation of a single-surface SPP on air–gold interface at different interface electric field amplitudes: dashed, 12 GV/m; circles, 11.5 GV/m; crosses, 11 GV/m; diamonds, 10.5 GV/m; triangles, 10 GV/m; stars, 9.5 GV/m. The inset is the nonlinear effective index normalized by the linear one versus the wavelength and field amplitude. (From Reference 19.)
2.3.2 Plasmon Solitons
Diffraction of electromagnetic (light) beams can be mitigated by nonlinearity, resulting in the generation of solitons—wave packets that maintain (roughly speaking) their envelopes as invariants during propagation. Solitons are one of the most explored features in nonlinear optics (and nonlinear physics in general). In this section we present solitons on planar metal–dielectric structures considering nonlinearities of one or both material components.
One of the prominent advantages of incorporating plasmons in nonlinear schemes is the capability to reduce modal volumes below classical limit of diffraction [45]. Tapered or corrugated plasmonic waveguides provided nanofocusing of optical fields [46] with apparent larger confinement in metal–insulator–metal (MIM) structures [47, 48]. Generally, nonlinear dispersion relations for MIM waveguides with even-order nonlinearities (Kerr or higher) may be derived if lateral confinement is neglected [49]. When the confinement is taken into account (in Kerr-nonlinear slab, bounded by silver claddings) hybrid-vector spatial plasmon solitons may emerge. The most striking effect of plasmonics is that when the separation between the two silver layers of the MIM structure is reduced to increase the transverse confinement into the deep subwavelength regime, the field envelope in the lateral dimension (bound only by the nonlinearity) is reduced as well [50], which is an inverse effect compared to a nonlinear all-dielectric waveguide. The plasmon soliton scenario may be formulated in terms of nonlinear Schrödinger equation as follows:
(2.9)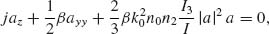 
where I and I3 are certain field averages across the waveguide transversal direction, k0 the free-space wavevector amplitude, and n0 and n2 the linear and nonlinear (Kerr) refractive indexes of the MIM core, respectively.
The first-order plasmon soliton with peak amplitude η and the width Δy is given by
(2.10)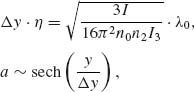 
where λ0 is the free-space wavelength.
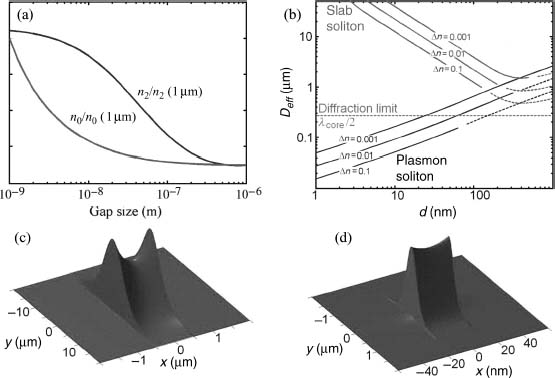
Simulation results show that the reduction of the gap between silver cladding layers increases the linear effective index (n0) of the fundamental plasmonic mode together with the effective nonlinearity (n2) (Fig. 2.4a). Calculation of the effective modal volume shows the ability of plasmon soliton mode to go beyond classical diffraction limit, while classical dielectric slabs, composed of positive permittivity materials, are not capable to support solitons with such properties (Fig. 2.4b). Finally, the corresponding soliton envelopes are depicted in Figures 2.4c and 2.4d, calculated for certain model parameters, indicated in the figure captions. The propagation length of the mode was shown to be larger than the typical soliton length as well as the decaying length due to metal absorption, clearing the possibility of soliton phenomenon in this structure.
FIGURE 2.4 (a) Normalized linear and nonlinear effective indexes inside plasmonic gap at λ0 = 1.5 μm. (b) Effective modal size Deff versus gap thickness of the nonlinear Kerr slab embedded in (blue) metal and (red) air. λ0 = 820 nm, n0 = 1.5. Intensity distributions of plasmon soliton beam in Kerr medium embedded within silver layers. (c) Δn = 0.005, λ0 = 1550 nm, d = 1 μm, 
m = –103.5 – i10, Deff = 2.4 μm. (d) Δn = 0.1, λ0 = 820 nm, d = 30 nm, m = –30.2 – i1.6, Deff = 95 nm. (From Reference 51.)
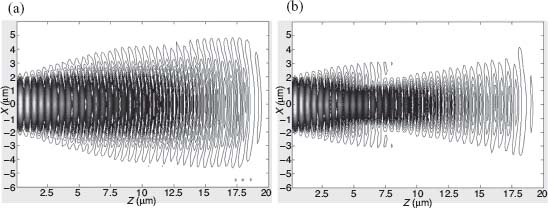
Nonlinear propagation of SPPs on the boundary of a metal and a nonlinear Kerr dielectric in the presence of losses was further considered and a self-focusing phenomenon with the formation of slowly decaying spatial solitons was numerically approved in Reference 52. While References 50 and 52 used Kerr dielectric media, a similar phenomenon may also occur due to the ponderomotive nonlinearity of the metal film itself. Finite difference time domain (FDTD) simulation of SPP propagation in a plasmonic MIM waveguide comprising a narrow linear dielectric medium between two metallic layers showed nanofocusing features for high field intensities. MIM-plasmon has higher (compared to single surface) mode overlap with metal cladding. Figure 2.5a shows the diffraction pattern of MIM SPP for different initial powers. In the low-power regime the regular in-plane diffraction pattern combined with propagation losses is observed. Self-focusing of the SPP mode is achieved due to the ponderomotive nonlinearity at field intensities as low as ∼kW/μm2 making SPP self-focusing a practically achievable phenomenon and is depicted in Figure 2.5b.
FIGURE 2.5 Nonlinear propagation in MIM: (a) beam diffraction at linear regime; (b) self-focusing due to ponderomotive nonlinearities of metal claddings.
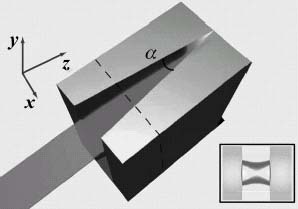
An interesting approach for partially overcoming propagation losses of plasmon soliton in MIM structure was proposed in Reference 53, where additional tapering at a properly chosen angle generates additional field concentration thus enhancing the field intensity and enabling longer propagation (Fig. 2.6).
FIGURE 2.6 Schematic of the three-dimensional plasmon focusing in a tapered slot waveguide. Focusing occurs in the horizontal plane, due to a taper, and in the vertical plane, due to the nonlinear self-focusing effect. Inset shows the waveguide cross section with the magnetic field distribution of a symmetric plasmon mode. (From Reference 53.)
The propagation losses may be compensated by incorporation of an active medium—spatial surface plasmon solitons on the metal stripe surrounded by active and passive dielectric media were proposed [54]. Stable solitons are achieved by proper coupling between SPPs propagating along the active and passive interfaces.
Multilayered metallo-dielectric structures with embedded nonlinearities may lead to the creation of the so-called discrete solitons. Arrays of coupled waveguides are known to produce discrete diffraction patterns, where mode, launched into a central waveguide, exhibits maximal intensity in some edge waveguides at the output. This diffraction may be suppressed by introduction of nonlinearity into one or more of the material components. Discrete solitons on nanoscale were studied in Reference 55 and were shown to be considerably different from conventional nonlinear dielectric waveguide arrays by combined interplay between periodicity, nonlinearity, and SPPs.
2.3.3 Nonlinear Plasmonic Waveguide Couplers
While many nonlinear SPP-based devices are feasible, we exemplify this notion by looking at an example of nonlinear couplers.
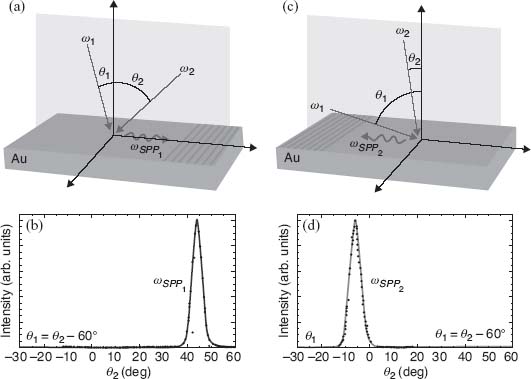
Plasmonic traveling modes (as well as any propagating modes) are “dark” since their propagation constants are always higher than those of the core dielectric media. This is the reason that the excitation of surface plasmons requires additional effort, such as implementation of Kretschmann/Otto configurations or etching of spatial gratings. However, free-space excitation of surface plasmons may also be assisted by nonlinear effects. One of the examples is nonlinear FWM, where fulfillment of phase-matching conditions involves the momentum of the resulting wave to be equal to the vector combination of momenta of three incident waves [56]. If the resulting combination results in momentum that can be satisfied only by the SPP, only this latter wave will have the maximal probability to be generated. In this scheme, SPPs may be excited on a metal surface by the overlap of two laser beams, incident from different angles to the normal. Two beams with λ1 = 707 nm and λ2 = 800 nm were used; fixing the angle of one beam, efficient excitation of surface plasmon occurs at a respective angle of the second beam. The generated SPP is monitored by outcoupling using the spatial grating etched on the surface (Fig. 2.7).
FIGURE 2.7 (a and c) Experimental configuration with overlaid scanning electron microscope images of the sample surface showing the gratings used for SPP outcoupling. The figures illustrate the resonant incident angles (arrows) and the direction of SPP propagation (wavy lines). (a) Configuration for plasmon λSPP1 = 633 nm excited by ωSPP1 = 2ω1 − ω2. (c) Configuration for plasmon λSPP2 = 921 nm excited by ωSPP2 = 2ω2 − ω1. (b and d) Experimental results showing the intensity of the outcoupled surface plasmons as a function of excitation angle Θ2 using Θ1 = Θ2 − 60°. Black dots are data and the solid curves are Gaussian fitting functions. The peak positions agree with the theoretical predictions in Equation 2.4. (Taken from Reference 56.)
This principle may be further extended and used for imaging of small objects, scattering the nonlinear signal to a far field, with subsequent detection [57]. The conceptual structure for FWM generation, combining local and grating resonances, was shown to enhance the nonlinear phenomena by three orders of magnitude [58]. Directional coupler based on coupled nonlinear MIM waveguides was investigated in Reference 59 and was shown to have substantial novel characteristics compared to pure dielectric nonlinear devices. Electrically controlled optical modulator creating modulated higher harmonics signal, originating from nonlinear dielectric material within the nanometric slit in a metal film, was demonstrated [60]. Power-dependent modal dispersion and switching was proposed in metallo-dielectric nanoparticle chain, embedded in nonlinear Kerr dielectric [61]. Two resonant modes are supported by the structure in the linear regime—longitudinal and transversal, which are different by 20 nm. Nonlinearities are shifting the mode resonances and mixing them up modifying the overall transmission.
2.4 LOCALIZED SURFACE PLASMON NONLINEARITY
Most of the current research on plasmonic enhancement of nonlinear interactions is related to localized surface plasmons generated near metallic nanoparticles, nanoantennas, and metamaterials based on such particles. Metallic nanoparticles at or near their plasmonic resonance generate highly localized electric field intensities that effectively correspond to light stopping at their vicinity. Varieties of nanoparticles and their constellations (e.g., dimers) were shown to enhance the local field and thus improve light–matter interactions. Nonlinear processes experience high-order enhancements due to their dependence on higher orders of the field amplitude, for example, SERS cross-section improvement up to 14 orders of magnitude. The nanoparticle interactions are conceptually similar to cavity-based enhancement of nonlinear phenomena. We first discuss this similarity and further look at a few interesting examples of nonlinear enhancement of the vacuum field and of non-perturbative high harmonic generation. We end this section by dealing with the limitation of extremely intense nonlinear localized plasmonics.
2.4.1 Cavities and Nonlinear Interactions Enhancement
The cavity concept serves as a transition between the propagating (of previous section) and localized surface plasmons. While cavities can be implemented in waveguide structures [62], when the latter are becoming shorter in dimension, they eventually collapse into the category of localized plasmon of a nanoparticle. Although the dimensions of the latter are typically in the extreme subwavelength regime, propagation effects are sometimes important for its nanocavity characteristics [63]. While all types of cavities are predominantly “stopped light” devices, the plasmonic nanoparticles enable virtually close to zero volume electric field intensity confinement. In terms of linear phenomena, the enhancement of the spontaneous emission rates in cavities relative to the free space is described in terms of the so-called Purcell factor [64], given by
(2.11)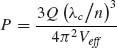 
where P is the Purcell enhancement factor, depending on the cavity quality factor Q, central wavelength λc, average modal refractive index n, and effective cavity modal volume Veff. Quality factors of ultra small plasmonic cavities are limited by the ratio of real-to-imaginary parts of electric permittivity (generally dozens at optical and near-infrared range) and cannot be improved much. On the other hand, the modal volumes may go far below the diffraction limit, approaching zero values in theoretical estimations [63]. Relying on the above, the linear Purcell factor in plasmonic environment may reach extremely high values. In terms of nonlinear phenomena, the cavity enhancement will improve the interaction, multiplying the effect by Purcell factor in power, equal to the order of nonlinear process. Thus SHG may be improved by a factor of P2 if the cavity is resonant at the doubled frequency.
In addition to local enhancement of the field (reduction of the mode volume), a short cavity may assist the generation of macroscopic nonlinear signal, by overcoming the required phase-matching condition. In parametric processes, for example, SHG, the pump frequency (ω) and the resulting doubled frequency (2ω) are generally not propagating with the same phase velocity due to dispersion of the nonlinear structure. Various phase-matching techniques may compensate this phase mismatch resulting in constructive interference for the nonlinear process making the whole structure to act as a macroscopic source of nonlinearity. In cavity nonlinear optics, however, the standing waves (for a cavity based on a waveguide structure) or the quasistatic fields (in localized plasmonic cavity) are generating different mechanism replacing the phase-matching. The proper theory, accompanied by experimental demonstration, was reported in Reference 65. The plane wave expansion, commonly used for propagating nonlinear optics, is replaced by eigen mode expansion in terms of cavity modes:
(2.12)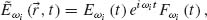 
where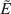 
ωi (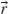, t) is the total electrical field with central frequency ωi, Eωi (t) the slowly varying time-dependent amplitude, and Fωi (t) the spatial mode dependence. The wave equation with nonlinear polarization as the source term may be written in terms of the above mode expansion, resulting in the following equation for the second harmonic field:
(2.13)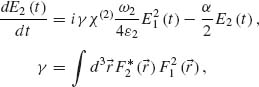 
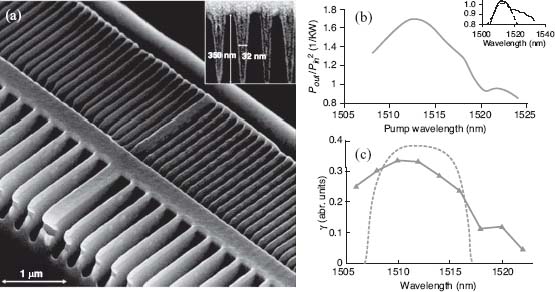
where α is a linear cavity loss, ε2 the cavity material permittivity at ω2, χ(2) the nonlinear susceptibility of the cavity, and γ the nonlinear mode overlap. It may be clearly seen that the classical phase-matching condition in cavity nonlinear optics should be replaced by the modal overlap. Hence, properly designed cavities, resonant at both fundamental and second harmonics, with spatially overlapping fields may dramatically enhance the nonlinear conversion efficiency. The first photonic example of such a design is presented in Figure 2.8.
FIGURE 2.8 (a) Scanning electron microscopy (SEM) image of the fabricated integrated double-resonance microcavity. The inset is a SEM cross-section image of the shortest period grating. (b) Measured SH generation efficiency Pout/Pin2 wavelength dependence. The inset is the microcavity transmission spectrum around the 1512 nm resonance. The solid curve is the measured and the dashed curve is the calculated (FDTD) spectrum. (c) Nonlinear mode overlap γ wavelength dependence. The solid curve is the measured and the dashed curve is the calculated spectrum. (From Reference 65.)
The advantage of doubly resonant plasmonic structure was demonstrated for surface-enhanced Raman spectroscopy, where a pair of particles provides the desired resonant structure for both pump and Stokes frequencies [66].
SHG from core–shell nanocavities, containing nonlinear material, was demonstrated to enhance the process by two to three orders of magnitude owing to the nonlinear core [67]. Surface patterning of core–shell geometry with nanogaps filled by GaAs was shown to enhance second harmonic signal at the spectral window collocated with minimal linear transmission [68]. Grooves, etched in a metal surface, carefully organized into grating geometry, were shown to enhance FWM efficiency by two orders of magnitude [58]. Improvement of FWM by four orders of magnitude was demonstrated during the creation of plasmonic dimer configuration, when one particle was brought in proximity to another attached to an NSOM tip [69]. Dark plasmonic modes (weakly coupled to far-field radiation) may be excited via second harmonic generation [70].
2.4.2 Enhancement of Nonlinear Vacuum Effects
Plasmonic cavities may also influence the properties of nonlinear emitters. It may be shown that emitters with initially low radiation efficiency may be substantially improved by plasmonic structures [71]. One of the very exciting processes with potential applications in quantum computing, transmission, and imaging is spontaneous two-photon emission (STPE), where electron–hole recombination process is accompanied by spontaneous emission of a photon pair. The process was recently observed using semiconductor structures [72] and subsequently enhanced by almost three orders of magnitude by depositing plasmonic array of bow-tie antennas on the top of semiconductor bulk [73]. STPE is an inherently weak second-order quantum-mechanical process and hence requires significant enhancement for competing with other candidates (such as SPDC) for various applications. The emission spectrum of STPE is very broadband since each pair of photons may be emitted with any energy combination with the only restriction on the overall energy conservation of the whole process. Dielectric cavities with high quality factors (Q) have very narrow spectral bandwidths. Such cavities fail to enhance the broadband STPE process. Contrarily, plasmonic cavities may exhibit significant Purcell factors by the reduction of modal volumes, while keeping quality factors to be relatively low. The relative nonlinear enhancement by a cavity may be roughly estimated by the ratio of the modified radiative density of states to the free-space values:
(2.14)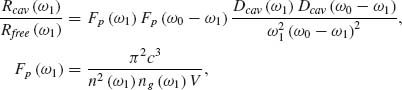 
where Rcav and Rfree are the STPE rate densities (at ω1) within the cavity and free space, respectively, Dcav the cavity spectral response (assumed to have a Lorentzian shape), and ω0 the bandgap transition frequency. Fp (ω1) is the usual density of states in homogeneous material with refractive and group indexes of n (ω1) and ng (ω1), respectively, and effective volume V. For a single-resonance wideband cavity, the maximal enhancement is obtained for a resonance, centered at ω0/2—when the two emitted photons are degenerate in frequency. The experimental structure was comprised of a 200 nm AlGaAs active layer, with one photon photoluminescence centered at 826 nm, and STPE peak at 1653 nm. A 60 nm thick gold bow-tie antenna array was fabricated on the surface of the active layer using e-beam lithography and was designed to have its plasmonic resonance at ω0/2 (Fig. 2.9a). The active layer was pumped optically.
FIGURE 2.9 (a) Transmission spectrum of the passive bow-tie particle array. (b) Spectrum of the enhancement in TPE by the bow-tie array: measurement, solid blue line; FDTD calculation, dashed black line. The inset is the one-photon emission spectrum. (From Reference 73.)
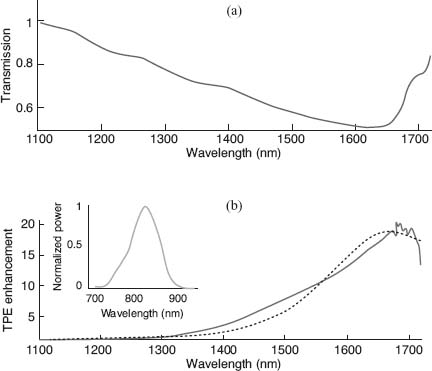
The resulting enhancement (Fig. 2.9b) of STPE was achieved over a relatively wide spectral range and by the directly measured value of enhancement factor of ∼20, and subtracting the background emission that was not enhanced, effective enhancement of about three orders of magnitude was exhibited—making this interesting nonlinear emission process to be close in intensity to regular LED emission.
2.4.3 High Harmonic Generation
The generation of high harmonics is applicable for coherent x-rays sources, laser processing, and attosecond spectroscopy. First experimental realizations considered flat metallic mirrors, while harmonics were generated by reflection. For example, 15th harmonic order, corresponding to a wavelength of 55.3 nm, was observed [74].
High harmonic generation was demonstrated recently by using localized plasmonic structures—specifically an array of bow-tie antennas, deposited on sapphire substrate [75]. The source of the nonlinear generation was a jet of argon gas, which was ionized by short femtosecond pulses (10 fs). Intense laser pulse causes ionization of core electrons, which are recaptured by the core atom, when the electrical field is reversed in direction. Acceleration of these electrons against the positively charged core produces “Bremsstrahlung” radiation resulting in a comb of higher harmonics. The required laser intensity for such ionization processes is very high (the threshold in this particular case is 1013 W/cm2), while the initial laser intensity provided 1011 W/cm2—two orders of magnitude lower than required. The plasmonic structure was capable by local field enhancement to support the missing two orders of magnitude. The maximal field enhancement was achieved within 20 nm gap between the nanoantennas, which is important to prevent the damage of both substrate and antenna materials. This reported experiment opens the avenue for additional extreme nonlinear nanoplasmonic applications, already showing competitive performances.
It was theoretically shown that there are additional contributions to high harmonic generation, beyond the local field enhancement. Particularly, inhomogeneity of the local field profile and electron absorption by the metal surface contribute to the generation of even harmonics and a significantly enhanced highest harmonic cutoff [76].
2.4.4 Localized Field Enhancement Limitations
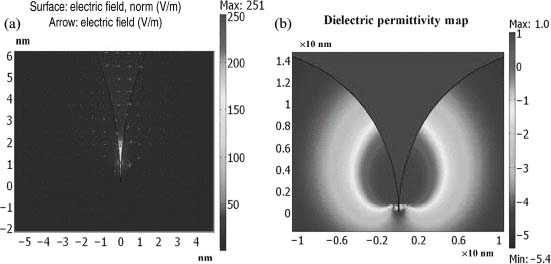
Limitation of the field enhancement, even before material damage sets in, may result from plasma effects. The predicted nonlinear cutoff on propagating plasmons discussed in Section 2.3.1 may also be applied to study the limitation of local field enhancement, associated with localized plasmon resonances of nanometallic particles. This limitation may be demonstrated through the vehicle of SERs. SERS is a very powerful tool for studying molecular structures, investigating their internal vibrational degrees of freedom. Raman scattering is a third-order process in quantum-mechanical description and inherently very weak and inefficient. However, by attaching a molecule to a rough metallic surface, or a metallic nanoparticle and relying on their local field enhancement, it is possible to increase the process efficiency by factors as high as 1014 relative to the scattering process in regular dielectric media. Electromagnetic theory explains this giant scattering rate enhancement by excitation of collective oscillations of electrons on the surface, coupled to external light field, namely plasmons, that modifies the local density of radiation states, resulting in two-order enhancement of the scattering efficiency. The overall scattering enhancement factor due to plasmonic cavity is proportional to E4, where E is the local field enhancement factor. This local field enhancement on metal surfaces strongly depends on the detailed surface geometry as well as on the chromatic dispersion of the metal itself. Complete theoretical model of SERS is very involved and still remains a subject of intensive research. Additional theoretical considerations (beyond electromagnetic), such as chemical considerations on formation of charge-transfer complexes, were shown to affect SERS efficiency as well [77]. Nevertheless, most of the experimental observations of enhanced nonlinear phenomena were explained by theory. Some of the reported SERS experiments were performed with excitation fields with low intensities, for example, 10 mW on 100 μm2 [6, 78] where noble metals can be treated as a linear dielectric. However, for higher excitation intensities the emergence of significant nonlinear ponderomotive effects may cause the field localization to disappear. In order to demonstrate this limitation, cylindrically shaped roughness on a flat metal surface may be investigated—in a similar way as is done for calculation of SERS enhancement [79]. The linear solution of such a quasi-static scenario (in principle, may be analytically solved) is depicted in Figure 2.10a for touching silver bumps of 15 nm radius. This specific geometry generates resonant conditions at a frequency where = –5.4 + 0.4j, including the material losses [80]. Incident beam with electrical field amplitude of 109 V/m and 460 nm free-space wavelength and polarization, parallel to the surface, will generate local fields, repelling the free electrons out of the high-intensity regions of the structure. The dielectric permittivity—depending on the local carrier concentration—is thus modified and recalculated accordingly to the linear solution and Equation 2.5, and the resulting permittivity distribution is shown in the color map depicted in Figure 2.10b. It can be clearly seen that the free carriers have been almost completely depleted from the region of interest, thus destroying the geometry of the confining potential. The complete self-consistent solution of such a nonlinear problem is involved, since the effect cannot be solved perturbatively and linear solution is not a good first estimate anymore.
FIGURE 2.10 (a) Linear solution of cylindrical bumps—E/E0. Field enhancement factor is about 251 at resonant condition. (b) Dielectric constant map at an external exciting field of 109 V/m. In the metal regions near the narrowest gap, the dielectric constant is now very close to the vacuum value. (From Reference 79.)
2.5 SUMMARY
In this chapter we presented some major activities in the field of nonlinear nanoplasmonics. A large number of recent scientific publications on this topic are emphasizing its significance and, of course, we could not cover all the facets of this subject in this chapter. We emphasized the uniqueness of metal and its support of nonlinear effects associated with free-electron plasma. Nonlinear devices, based on nonlinear optical modes and spatial solitons in waveguide structures, were discussed. Nonlinear effects in nanoplasmonic cavities were presented—unifying propagating and localized plasmons for distinctive improvement of nonlinear light–matter interactions at deep subwavelength scale.
Progress in technological, computational, and experimental capabilities of last decades in the field of nanoscience made numerous theoretical propositions of the past to be experimentally relevant in the present and near future and is already pushing reconsideration and investigation of new nanoscale phenomena. In this sense the field of nonlinear nanoplasmonics is situated at this special interface between “old school” and recent “technological edge.” It is still too premature to claim that plasmonics with its nonlinear aspects will be a cornerstone for major future devices like electronics does for current devices. However, it has already initiated a boost in science and technology, bringing new concepts of thinking and tackling various fundamental and technological problems.
ACKNOWLEDGMENTS
P. Ginzburg acknowledges the Royal Society for Newton International Fellowship and Yad Hanadiv for Rothschild Fellowship.
REFERENCES
1. Franken PA, Hill AE, Peters CW, Weinreich G (1961) Generation of optical harmonics. Phys. Rev. Lett. 7: 118–119.
2. Burnett NH, Baldis HA, Richardson MC, Enright GD (1977) Harmonic generation in CO2 laser target interaction. Appl. Phys. Lett. 31: 172.
3. Gerstner E (2007) Laser physics: extreme light. Nature 446: 16–18.
4. Steen WM, Mazumder J, Watkins KG (2010) Laser Material Processing. 4th ed. Springer.
5. Louisell WH, Yariv A, Siegman AE (1961) Quantum fluctuations and noise in parametric processes. I. Phys. Rev. 124: 1646–1654.
6. Nie S, Emory SR (1997) Probing single molecules and single nanoparticles by surface-enhanced Raman scattering. Science 275: 1102–1106.
7. Agranovich VM, Ginzburg VL (1984) Crystal Optics with Spatial Dispersion, and Excitons. Springer.
8. Boyd RW (2008) Nonlinear Optics. 3rd ed. Academic Press.
9. Yariv A, Yeh P (2006) Photonics: Optical Electronics in Modern Communications. 6th ed. Oxford University Press.
10. Khurgin J (1988) Second-order nonlinear effects in asymmetric quantum-well structures. Phys. Rev. B 38: 4056–4066.
11. Ginzburg P, Hayat A, Orenstein M (2007) Nonlinear optics with local phasematching by quantum based meta-material. J. Opt. A Pure Appl. Opt. 9: S350.
12. Piredda G, Smith DD, Wendling B, Boyd RW (2008) Nonlinear optical properties of a gold-silica composite with high gold fill fraction and the sign change of its nonlinear absorption coefficient. J. Opt. Soc. Am. B 25: 945.
13. Lepeshkin NN, Schweinsberg A, Piredda G, Bennink RS, Boyd RW (2004) Enhanced nonlinear optical response of one-dimensional metal-dielectric photonic crystals. Phys. Rev. Lett. 93: 123902.
14. Perner M, Bost P, Lemmer U, von Plessen G, Feldmann J, Becker U, Mennig M, Schmitt M, Schmidt H (1997) Optically induced damping of the surface plasmon resonance in gold colloids. Phys. Rev. Lett. 78: 2192.
15. Jiang L, Tsai H (2005) Improved two-temperature model and its application in ultrashort laser heating of metal films. J. Heat Transfer 127: 1167.
16. Link S, El-Sayed MA (1999) Spectral properties and relaxation dynamics of surface plasmon electronic oscillations in gold and silver nanodots and nanorods. J. Phys. Chem. B 103(40): 8410–8426.
17. Wurtz GA, Pollard R, Hendren W, Wiederrecht GP, Gosztola DJ, Podolskiy VA, Zayats AV (2011) Designed ultrafast optical nonlinearity in a plasmonic nanorod metamaterial enhanced by nonlocality. Nat. Nanotechnol. 6: 107–111.
18. Nicholson DR (1983) Introduction to Plasma Theory. 2nd ed. John Wiley & Sons.
19. Ginzburg P, Hayat A, Berkovitch N, Orenstein M (2010) Nonlocal ponderomotive nonlinearity in plasmonics. Opt. Lett. 35: 1551.
20. Bennemann KH (1998) Non-linear Optics in Metals. Clarendon Press.
21. Palomba S, Harutyunyan H, Renger J, Quidant R, van Hulst NF, Novotny L (2011) Nonlinear plasmonics at planar metal surfaces. Phil. Trans. R. Soc. A 369: 3497–3509.
22. Bloembergen N, Chang RK, Jha SS, Lee CH (1968) Optical second-harmonic generation in reflection from media with inversion symmetry. Phys. Rev. 174: 813–822.
23. Jha SS (1965) Theory of optical harmonic generation at a metal surface. Phys. Rev. 140: A2020–A2030.
24. Sipe JE, So VCY, Fukui M, Stegeman GI (1980) Analysis of second-harmonic generation at metal surfaces. Phys. Rev. B 21: 4389–4402.
25. Xiang Wang F, Rodríguez FJ, Albers WM, Ahorinta R, Sipe JE, Kauranen M (2009) Surface and bulk contributions to the second-order nonlinear optical response of a gold film. Phys. Rev. B 80: 233402.
26. Centini M, Benedetti A, Sibilia C, Bertolotti M, Scalora M (2009) Second harmonic generation from metallic 2D scatterers. Proc. SPIE 7354: 73540F.
27. Brown F, Parks RE, Sleeper AM (1965) Nonlinear optical reflection from a metallic boundary. Phys. Rev. Lett. 14: 1029–1031.
28. Klein MW, Enkrich C, Wegener M, Linden S (2006) Second-harmonic generation from magnetic metamaterials. Science 313: 502–504.
29. Goff JE, Schaich WL (1997) Hydrodynamic theory of photon drag. Phys. Rev. B 56: 15421–15430.
30. Gibson AF, Kimmit MF, Walker AC (1970) Photon drag in germanium. Appl. Phys. Lett. 17: 75–77.
31. Vengurlekar AS, Ishihara T (2005) Surface plasmon enhanced photon drag in metals. Appl. Phys. Lett. 87: 091118.
32. Kurosawa H, Ishihara T (2012) Surface plasmon drag effect in a dielectrically modulated metallic thin film. Opt. Express 20: 1561–1574.
33. Durach M, Rusina A, Stockman MI (2009) Giant surface plasmon induced drag effect (SPIDER) in metal nanowires. Phys. Rev. Lett. 103 186801-1-4.
34. Varró S, Ehlotzky F (1994) Higher-harmonic generation from a metal surface in a powerful laser field. Phys. Rev. A 49: 3106–3109.
35. Farkas Gy, Tóth Cs, Moustaizis SD, Papadogiannis NA, Fotakis C (1992) Observation of multiple-harmonic radiation induced from a gold surface by picosecond neodymium-doped yttrium aluminum garnet laser pulses. Phys. Rev. A 46: R3605.
36. Georges AT (1996) Coherent and incoherent multiple-harmonic generation from metal surfaces. Phys. Rev. A 54: 2412–2418.
37. Papadogiannis NA, Loukakos PA, Moustaizis SD (1999) Observation of the inversion of second and third harmonic generation efficiencies on a gold surface in the femtosecond regime. Opt. Commun. 166: 133–139.
38. Lippitz M, van Dijk MA, Orrit M (2005) Third-harmonic generation from single gold nanoparticles. Nano Lett. 5(4): 799–802.
39. Ho JR, Grigoropoulos CP, Humphrey JAC (1995) Computational study of heat transfer and gas dynamics in the pulsed laser evaporation of metals. J. Appl. Phys. 78: 4696.
40. Marla D, Bhandarkar UV, Joshi SS (2011) Critical assessment of the issues in the modeling of ablation and plasma expansion processes in the pulsed laser deposition of metals. J. Appl. Phys. 109: 021101.
41. Güdde J, Hohlfeld J, Müller JG, Matthias E (1998) Damage threshold dependence on electron-phonon coupling in Au and Ni films. Appl. Surf. Sci. 127–129: 40–45.
42. Tribelsky MI, Miroshnichenko AE, Kivshar YS, Luk'yanchuk BS, Khokhlov AR (2011) Laser pulse heating of spherical metal particles. Phys. Rev. X 1: 021024.
43. Pronko PP, Dutta SK, Squier J, Rudd JV, Du D, Mourou G (1995) Machining of sub-micron holes using a femtosecond laser at 800 nm. Opt. Commun. 114: 106–110.
44. Mihalache D, Bertolotti M, Sibilia C (1989) Nonlinear wave propagation in planar structures. In: Wolf E, editor. Progress in Optics. Vol. 27. Elsevier. Chapter 4.
45. Gramotnev DK, Bozhevolnyi SI (2010) Plasmonics beyond the diffraction limit. Nat. Photonics 4: 83–91.
46. Stockman MI (2004) Nanofocusing of optical energy in tapered plasmonic waveguides. Phys. Rev. Lett. 93: 137404.
47. Ginzburg P, Arbel D, Orenstein M (2006) Gap plasmon polariton structure for very efficient microscale to nanoscale interfacing. Opt. Lett. 31: 3288–3290.
48. Ginzburg P, Orenstein M (2007) Plasmonic transmission lines: from micro to nano scale with λ/4 impedance matching. Opt. Express 15: 6762–6767.
49. Rukhlenko ID, Pannipitiya A, Premaratne M, Agrawal GP (2011) Exact dispersion relation for nonlinear plasmonic waveguides. Phys. Rev. B 84: 113409.
50. Feigenbaum E, Orenstein M (2007) Plasmon soliton. Opt. Lett. 32: 674–676.
51. Feigenbaum E, Orenstein M (2007) Modeling of complementary (void) plasmon waveguiding. J. Lightw. Technol. 25(9): 2547–2562.
52. Davoyan AR, Shadrivov IV, Kivshar YS (2009) Self-focusing and spatial plasmon-polariton solitons. Opt. Express 17: 21732–21737.
53. Davoyan AR, Shadrivov IV, Zharov AA, Gramotnev DK, Kivshar YS (2010) Nonlinear nanofocusing in tapered plasmonic waveguides. Phys. Rev. Lett. 105: 116804.
54. Marini A, Skryabin DV, Malomed B (2011) Stable spatial plasmon solitons in a dielectric-metal-dielectric geometry with gain and loss. Opt. Express 19: 6616–6622.
55. Liu Y, Bartal G, Genov DA, Xiang Z (2007) Subwavelength discrete solitons in nonlinear metamaterials. Phys. Rev. Lett. 99: 153901.
56. Renger J, Quidant R, van Hulst N, Palomba S, Novotny L (2009) Free-space excitation of propagating surface plasmon polaritons by nonlinear four-wave mixing. Phys. Rev. Lett. 103: 266802.
57. Harutyunyan H, Palomba S, Renger J, Quidant R, Novotny L (2010) Nonlinear dark-field microscopy. Nano Lett. 10(12): 5076–5079.
58. Genevet P, Tetienne J, Gatzogiannis E, Blanchard R, Kats MA, Scully MO, Capasso F (2010) Large enhancement of nonlinear optical phenomena by plasmonic nanocavity gratings. Nano Lett. 10: 4880–4883.
59. Salgueiro JR, Kivshar YS (2010) Nonlinear plasmonic directional couplers. Appl. Phys. Lett. 97: 081106.
60. Cai W, Vasudev AP, Brongersma ML (2011) Electrically controlled nonlinear generation of light with plasmonics. Science 333: 1720–1723.
61. Panoiu N-C, Osgood RM, Jr (2004) Subwavelength nonlinear plasmonic nanowire. Nano Lett. 4(12): 2427–2430.
62. Maier SA, Kik PG, Atwater HA (2003) Optical pulse propagation in metal nanoparticle chain waveguides. Phys. Rev. B 67: 205402.
63. Feigenbaum E, Orenstein M (2008) Ultrasmall volume plasmons, yet with complete retardation effects. Phys. Rev. Lett. 101(16): 163902.
64. Purcell EM, Torrey HC, Pound RV (1946) Resonance absorption by nuclear magnetic moments in a solid. Phys. Rev. 69: 37.
65. Hayat A, Orenstein M (2007) Standing-wave nonlinear optics in an integrated semiconductor microcavity. Opt. Lett. 32: 2864–2866.
66. Banaee MG, Crozier KB (2011) Mixed dimer double-resonance substrates for surface-enhanced Raman spectroscopy. ACS Nano 5(1): 307–314.
67. Pu Y, Grange R, Hsieh C, Psaltis D (2010) Nonlinear optical properties of core-shell nanocavities for enhanced second-harmonic generation. Phys. Rev. Lett. 104: 207402.
68. Fan W, Zhang S, Panoiu N-C, Abdenour A, Krishna S, Osgood RM, Malloy KJ, Brueck SRJ (2006) Second harmonic generation from a nanopatterned isotropic nonlinear material. Nano Lett. 6(5): 1027–1030.
69. Danckwerts M, Novotny L (2007) Optical frequency mixing at coupled gold nanoparticles. Phys. Rev. Lett. 98: 026104.
70. Biris CG, Panoiu NC (2011) Excitation of dark plasmonic cavity modes via nonlinearly induced dipoles: applications to near-infrared plasmonic sensing. Nanotechnology 22: 235502.
71. Khurgin JB, Sun G, Soref RA (2007) Enhancement of luminescence efficiency using surface plasmon polaritons: figures of merit. J. Opt. Soc. Am. B 24: 1968–1980.
72. Hayat A, Ginzburg P, Orenstein M (2008) Observation of two-photon emission from semiconductors. Nat. Photonics 2: 238.
73. Nevet A, Berkovitch N, Hayat A, Ginzburg P, Ginzach S, Sorias O, Orenstein M (2010) Plasmonic nanoantennas for broad-band enhancement of two-photon emission from semiconductors. Nano Lett. 10: 1848–1852.
74. von der Linde D, Engers T, Jenke G, Agostini P, Grillon G, Nibbering E, Mysyrowicz A, Antonetti A (1995) Generation of high-order harmonics from solid surfaces by intense femtosecond laser pulses. Phys. Rev. A 52: R25–R27.
75. Kim S, Jin J, Kim Y, Park I, Kim Y, Kim S (2008) High-harmonic generation by resonant plasmon field enhancement. Nature 453: 757–760.
76. Husakou A, Im S-J, Herrmann J (2011) Theory of plasmon-enhanced high-order harmonic generation in the vicinity of metal nanostructures in noble gases. Phys. Rev. A 83: 043839.
77. Lombardi JR, Birke RL, Lu T, Xu J (1986) Charge-transfer theory of surface enhanced Raman spectroscopy: Herzberg–Teller contributions. J. Chem. Phys. 84: 4174.
78. Kneipp K, Wang Y, Kneipp H, Perelman LT, Itzkan I, Dasari RR, Feld MS (1997) Single molecule detection using surface-enhanced Raman scattering (SERS). Phys. Rev. Lett. 78: 1667.
79. Ginzburg P, Hayat A, Orenstein M (2008) Breakdown of surface plasmon enhancement due to ponderomotive forces. Plasmonics and Metamaterials, October, Rochester, NY. OSA Technical Digest (CD), Optical Society of America, paper MThC8.
80. Pendry JB (2000) In: Soukoulis CM, editor. Intense Focusing of Light Using Metals, NATO ASI Series. Springer http://link.springer.com/chapter/10.1007%2F978-94-010-0738-2_24.