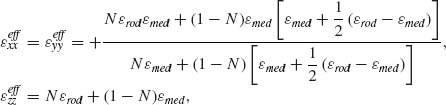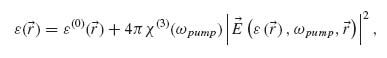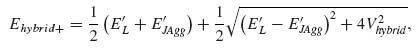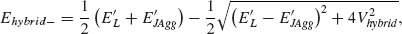3
Plasmonic Nanorod Metamaterials as a Platform for Active Nanophotonics
3.1 INTRODUCTION
Metamaterials consist of ensembles of subwavelength structures with an engineered electromagnetic response, so that their electromagnetic properties are determined not by the properties of the material constituents but rather by the structural geometry [1–3]. In the optical and near-infrared spectral ranges, metallic nanostructures support surface plasmon excitations associated with the free-electron motion near the interface between a metal and a dielectric. This behavior is central in achieving the required resonant properties of “meta-atoms” forming metamaterials. The plasmonic metamaterials are based on various combinations of metallic nanostructures, such as split-ring resonators of different geometries, fishnets, or nanorods. They provide the opportunity to flexibly design optical properties by engineering the optical response of individual components as well as the electromagnetic interaction between them. Metamaterials may exhibit unique properties such as negative permeability and negative refractive index and may be used to design super- and hyper-lenses for diffraction-unlimited high-resolution imaging and cloaking [1–11]. The most important practical advantage of metamaterials in active nanophotonic applications, where one needs to efficiently control optical signals with external stimuli, is in the possibility to readily design the dispersion of plasmonic modes and related active response. This can be electric or magnetic-field-tuned optical properties, mechanically or all-optically tuneable metamaterials, and photonic switches and modulators [12–17]. These enhanced functionalities can be optimized by engineering the required spectral response, the electromagnetic mode localization and field enhancement beneficial for many applications.
Dielectric, semiconductor, and metallic nanowires and nanorods have recently attracted significant attention due to their remarkable optical and electronic properties [18–21]. Among others, these include light guiding in subwavelength diameter metallic wires, negative permeability of pairs of closely spaced metallic rods, and optical plasmonic antennas [22–24]. These effects rely on surface plasmon modes supported by a metallic nanowire or nanorod. Progress in nanofabrication techniques has opened up the possibility to fabricate arranged metallic nanorods in macroscopic size arrays with their long axes aligned perpendicular to the substrate [25]. This geometry of oriented and closely packed nanorods, with a much reduced influence of the underlying substrate, impacts both the spectral optical properties and the spatial field distribution in the array, compared to isolated or weakly interacting nanorods studied in colloidal solutions [26, 27] or placed on substrates [23, 28].
Optical properties of such nanorod arrays featuring deep-subwavelength sizes in lateral direction can be described by effective permittivity parameters. Maxwell-Garnett (MG) calculations of the optical properties of these metamaterials have shown that the strongly anisotropic optical behavior can be beneficial for spectroscopic, sensing, as well as near-field optical imaging applications [29–33]. The important property of nanorod metamaterials is the possibility of wide range tuning of the geometrical parameters of the structure so as to control the electromagnetic interaction between the rods. This can be done, for example, by changing the inter-rod distance and is crucial for determining the reflection, transmission, and extinction of the array, and associated linear and nonlinear properties. This type of anisotropic plasmonic metamaterial exhibits unique optical properties such as hyperbolic dispersion and related strong Purcell effect, high-resolution imaging capabilities, high sensitivity to refractive index variations and biosensing, as well as active optical functionalities including enhanced nonlinear properties [3, 34, 36, 37].
This chapter presents the review of plasmonic metamaterials based on aligned nanorod assemblies. After a brief discussion of the fabrication, microscopic and effective medium description of the nanorod metamaterial will be detailed. The role of hyperbolic dispersion and epsilon-near-zero (ENZ) response will be discussed. We will then focus on the designs of active metamaterials. Nonlinear optical properties arising from the hybridization of plasmonic nanorod metamaterial and nonlinear dielectric as well as due to intrinsic metal nonlinearity will be presented. The role of weak and strong coupling regime of molecular excitons and plasmonic modes of the metamaterial on the optical properties will also be described. Finally, the electro-optical response of nanorod metamaterial hybridized with liquid crystals (LCs) will be discussed.
3.2 NANOROD METAMATERIAL GEOMETRY
The nanorod metamaterials consist of aligned nanorods oriented perpendicularly to a supporting substrate (Fig. 3.1). The nanorods are generally embedded in a dielectric matrix but can also be free-standing in air. Typically, they are grown electrochemically in a substrate-supported, porous, anodized aluminum oxide template (AAO) [25]. The diameter, separation, and ordering of the metallic rods in the assembly are determined by the geometry of the AAO template, which is in turn controlled by the anodization conditions and post-chemical etching processes. The rod diameter and spacing can vary in the range of 20–80 nm with separation between rods in the range of 40–100 nm. The rod diameter and separation are difficult to control independently on as-grown Al films, but they can be completely decoupled using pre-structured Al films [38, 39]. One-step anodization process provides a weakly disordered hexagonal periodic lattice of pores. Perfect hexagonal lattice ordering can be achieved with a two-step anodization process. By pre-structuring the Al film before anodization, arbitrary lattice geometry can be achieved as well [40, 41].
FIGURE 3.1 (a) Schematic representation of the nanorod metamaterial with parameter notations used throughout the chapter. (b) Scanning electron microscopy (SEM) image from a typical nanorod metamaterial made of Au nanorods. The AAO matrix was removed prior to SEM imaging, and the sample tilted with a viewing angle of 45°.
The length of the rods can be chosen by controlling the electrodeposition time and can be varied from about 20 nm to the limiting value dictated by the thickness of the AAO template, typically a few hundred nanometers. All these parameters—material of the rod, rod aspect ratio, rod length, and separation in the array—impact the optical response of the metamaterial. The rod material can be any metal suitable for electrodeposition including but not limited to Au, Ag, Ni, and Co.
In contrast to geometries involving nanorods on substrates or suspended in solutions, the nanorods forming a metamaterial have typically a much higher aspect ratio, are standing on a substrate with their long axes oriented perpendicularly to it, and are placed in a quasi-regular lattice. An example of nanorod assembly is shown in Figure 3.1 presenting an SEM image of the assembly of Au rods after removal of the AAO matrix to enable their observation. The metamaterial can be additionally structured to create laterally confined geometries. This can be done using post-growth processing, for example, laser ablation [42], structuring of the underlying electrodes, or controlling AAO pore openings by focused ion beam [38, 39, 43].
3.3 OPTICAL PROPERTIES
3.3.1 Microscopic Description of the Metamaterial Electromagnetic Modes
The optical properties of nanorod assemblies (Fig. 3.2a) are reminiscent of those of individual plasmonic nanorods. For the nanorod metamaterial, plane wave-coupled modes are determined by two dipolar resonances associated with localized surface plasmon (LSP) excitation parallel and perpendicular to the nanorod long axis. The resonance associated with electron motion perpendicular to the nanorod long axis is excited with light having electric field component along this direction and is approximately situated at 520 nm in wavelength. The resonance associated with the electron motion parallel to the long axis is in the infrared for the nanorods with aspect ratios larger than 5 (Fig. 3.2b). For example, an isolated nanorod with a diameter of 30 nm and an aspect ratio of 10 embedded in AAO exhibits a longitudinal dipolar resonance at around 2 μm (Fig. 3.2b). The resonance demonstrating similar polarization properties in the array of nanorods is observed in the visible region of the spectrum at around 650 nm, therefore, strongly blue-shifted compared to the expected position of the dipolar resonance. This resonance has the same polarization properties as isolated longitudinal LSP related to a dipolar excitation associated with a long nanorod axis and will be referred to as L-resonance in the metamaterial. In analogy, the complementary transverse mode of the metamaterial will be referred to as T-resonance as it is excited with an electric field component perpendicular to the nanorod long axis.
FIGURE 3.2 (a) Optical extinction spectra of the metamaterial measured at different angles of incidence for p-polarized light having an electric field component parallel to the nanorod long axis. The nanorods' length is 300 nm, diameter is 30 nm, their and the inter-rod distance is 60 nm. The nanorods are embedded in an AAO matrix. (b) L-resonance wavelength dependence on the aspect ratio for nanorods in the metamaterial (circles) and isolated ellipsoids (squares). (c) Schematic energy diagram of the plasmonic resonances in the metamaterial relative to the modes of individual nanorods. Strong electromagnetic coupling of the plasmonic resonances supported by individual nanorods leads to the formation of the collective plasmonic modes observed in (a).
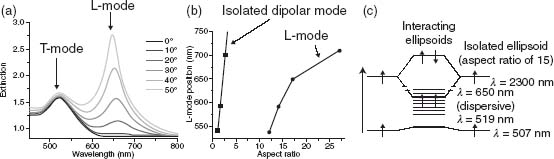
The observed behavior of the L-resonance can be explained by the formation of a spatially extended (collective) plasmonic resonance in the nanorod array due to the interaction between the plasmonic modes supported by individual nanorods in the assembly. In a simple consideration, this extended mode can be treated as a linear combination of these modes experiencing sensitive electromagnetic interaction from neighboring nanorods when kpl < 2π, where kp is the field extension of the LSP outside metal and l is the average distance between nanorods in the array. Considering the interaction between two nanorods only, coherent coupling between the longitudinal dipolar modes supported by these rods would result in the formation of two eigenstates representing the symmetric and antisymmetric configurations of the plasmonic dipole moments of the coupled rod system [51]. Including more interacting nanorods will result in the formation of a band of plasmonic states formed in the nanorod assembly.
This interaction is schematically shown in the energy diagram of Figure 3.2c where strong coupling between the nanorods shifts the symmetric state (parallel orientation of the dipole moments of the nanorods) in the short-wavelength spectral range compared to the longitudinal dipolar mode of the isolated nanorods. The antisymmetric state corresponds to the antiparallel arrangement of the dipole moments, is not optically active, and can be excited only in the near field.
The experimental extinction spectra –log10(T ), where T is the transmittance, measured for an array of Au nanorods embedded in an AAO matrix (n ≈ 1.6) are shown in Figure 3.2a for different angles of incidence. At normal incidence or also with s-polarized light, where the incident electric field vibrates perpendicular to the nanorod long axis, the spectra reveal the T-mode at around 520 nm in wavelength [29]. At oblique incidence and with p-polarized light, where the incident electric field has a component both along and perpendicular to the nanorod long axes, two peaks are observed in the spectra: the above-mentioned T-resonance as well as the L-resonance at a longer wavelength. This long-wavelength peak becomes more pronounced at larger angles of incidence for which the longitudinal LSP is excited more effectively. The angular sensitivity of the spectra of Figure 3.2a reflects the strong anisotropy of the structure defined by the orientation of the nanorods in the metamaterial. The general behavior of these two observed resonances is consistent with the response of the dipolar modes supported by isolated or weakly interacting rods [29].
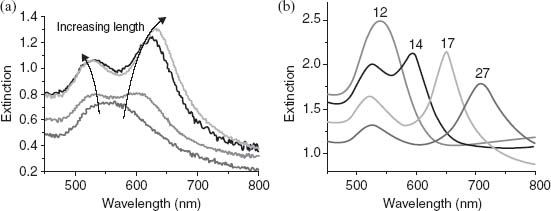
The L-resonance wavelength depends on both the rod aspect ratio and the distance between the rods in the array. In accordance with the dipolar plasmonic response of nanorods, an increase in the nanorod aspect ratio causes the two resonances to split further apart with the T-resonance undergoing a blue-shift while the L-resonance moves toward longer wavelengths. This behavior is illustrated in Figure 3.3 for either varying rod length (Fig. 3.3a) or varying rod diameter (Fig. 3.3b). The inter-rod distance can also be varied in order to tune the spectral position of the resonances in the array throughout the visible spectrum [45, 46]. Thus, this metamaterial provides excellent opportunities to control plasmonic resonances by controlling geometrical parameters of the nanorod arrays, such as the nanorod aspect ratio (and, thus, LSP wavelength for individual rods) as well as their separation (and, thus, the interaction between nanorods) resulting in the tunability of the metamaterial L-resonance from visible to near-infrared frequencies.
FIGURE 3.3 Optical extinction spectra of the metamaterial as a function of rod aspect ratio. (a) The nanorod length is varied from 100 to 250 nm for an inter-rod distance of 60 nm and a rod diameter of 30 nm. (b) The nanorod length is 400 nm and the inter-rod distance is about 60 nm. The curves are labeled according to the rod's aspect ratio corresponding to rods with diameter ranging from about 15 to 30 nm. The incident light is p-polarized. The angle of incidence is 40°.
The field distribution in the metamaterial associated with the collective plasmonic L-resonance evolves from LSP fields of individual nanorods (Fig. 3.4). For a larger inter-rod distance of 500 nm, the field distribution around the rods, modeled using finite-element method, is dominated by the dipolar mode of the longitudinal plasmon resonance occurring at a wavelength of around 1950 nm. In this case, the field is localized at the rods' extremities with a small breaking of symmetry due to the presence of the substrate and illumination conditions. The effect of a reduction in the inter-rod distance leads to a blue-shift of the L-resonance, consistent with both the results from the effective medium calculations, detailed in the next section, and experimental observations. With the increase of the inter-rod coupling observed for smaller inter-rod spacings, the spatial distribution of the electric field and the power flow in the array are significantly modified compared to weakly interacting rods. In fact, the electric field in this geometry concentrates within the metamaterial slab, in the middle part of the rods. This evolution corresponds to a simultaneous decrease of the field amplitude at the rods' extremities. This reconfiguration of the spatial distribution of the field in the array is supported by experimental observations that showed the lack of sensitivity in the spectral position of the array's extinction, and the L-resonance position in particular, when the index of refraction of the superstrate is modified, that is, when only the rods' extremities are subjected to a change in refractive index [47].
FIGURE 3.4 Electric field distribution in L-resonance plotted in the primitive cell of the nanorod array for different inter-rod distances: (a) 500 nm, (b) 200 nm, (c) 150 nm, and (d) 100 nm, calculated using the finite-element method. The nanorod length and diameter are 300 and 30 nm, respectively. The nanorods are embedded in AAO (refractive index n = 1.6) and supported by a glass substrate (n = 1.5). The superstrate is air (n = 1). The angle of incidence of TM-polarized probe light is 45°. The arrows in (a)–(d) show the direction of the Poynting vector.
It is instructive to examine the behavior of the Poynting vector within the assembly as a function of inter-rod coupling strength (Figs. 3.4a–3.4d). Going from the larger inter-rod distances to the strongly coupled regime, the electromagnetic energy flow around the rods evolves from being localized at the rods' extremities to a net energy flux in the layer containing the nanorods in a direction perpendicular to their long axes. Thus, the electromagnetic energy coupled to the array can effectively propagate from nanorod to nanorod within the metamaterial. In the geometry considered in the calculations, the maximum bandwidth of the L-resonance defined as BL = 2|ω0 − ωL|, where ω0 and ωL are the resonant frequencies of the dipolar longitudinal mode of the isolated nanorods and the L-resonance, respectively, is obtained for the smallest inter-rod distance and is estimated to be about 1.4 eV for an inter-rod distance of 100 nm. This corresponds to a maximum group velocity of about 1.7×107 m/s if a linear dependence of the group velocity with bandwidth is assumed. The rate at which energy is lost in the assembly would then correspond to 1.2×1013 Hz, considering the 100 meV homogeneous broadening of the L-resonance [44]. The damping rate follows a monotonous and decreasing function of the inter-rod coupling strength, supporting the observation that the formation of the L-resonance enables electromagnetic energy to propagate in the layer defined by the nanorod metamaterial.
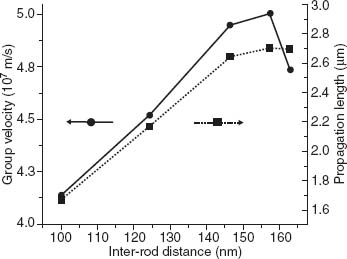
These properties were also investigated experimentally by gradually tuning the inter-rod coupling strength varying the inter-rod distance from about 170 to about 100 nm. This results in a shift of the L-resonance position from 1.74 to 2.25 eV [46]. Estimating the longitudinal resonance frequency of the isolated rod to be located around 0.54 eV, the effect of decreasing the inter-rod distance from 170 to 100 nm is to increase the bandwidth from 2.4 to 3.4 eV, respectively. Accounting for the bandwidth, the inter-rod distance, as well as the L-resonance linewidth, we can estimate the group velocity and propagation length of electromagnetic energy in the nanorod assembly. These quantities are plotted in Figure 3.5 as a function of inter-rod distance. The behavior of group velocity is quite interesting as it undergoes a nonmonotonous variation as a function of inter-rod coupling strength with a maximum obtained for an inter-rod distance of about 155 nm. In this case, a group velocity of about 5×107 m/s is reached, a value that is comparable to group velocities reported for other plasmonic guiding geometries [48, 49]. The origin of this maximum was associated to an increasing confinement of electromagnetic energy in the metamaterial as near-field interactions become predominant in the system with decreasing inter-rod distances [50].
FIGURE 3.5 Group velocity (dots) and propagation length (squares) of electromagnetic energy of the L-resonance as a function of inter-rod distance; a decreasing distance corresponds to an increasing coupling strength.
Defining the inter-rod coupling strength for the L-mode as J =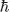 
|ω0 − ωL|, coupling strengths on the order of 1 eV are typically observed in assemblies of nanorods but, more importantly, can be easily varied in order to control the degree of localization of electromagnetic energy within the assembly. For comparison, coupling strengths on the order of 60 to 200 meV, depending on the polarization, have been measured for other plasmonic structures [51, 52], while calculations show that coupling strength comparable to our observations can be reached in more complex plasmonic systems made of chains of interacting plasmonic nanoparticles [53].
The flexible geometry in assemblies of nanorods opens new opportunities to tailor the optical properties of plasmonic resonances both spectrally and spatially. The L-resonance obtained for strongly interacting nanorods shows particular potential in applications associated with guiding electromagnetic energy and optical manipulation applications on the nanometric scale. These applications are relevant since the recent demonstrations of the possibility to produce laterally confined assemblies of nanorods with single nanorod resolution [54], the optical properties of which should allow even further design of the field profiles and enhancement.
3.3.2 Effective Medium Theory of the Nanorod Metamaterial
Several analytical theories have been developed in the past to attempt describing the optical responses of nanoparticles such as nanorods. Mie [55] and Gans [56] solved Maxwell's equations explicitly for spheres and spheroids while others have made use of an effective medium approach such as the MG theory [57, 58]. In this section we will briefly present the results obtained from an effective medium theory (EMT) approach that allows one to accurately investigate the optical properties of an anisotropic medium made of plasmonic nanorods.
The geometry of the nanorod composites considered in the model is shown in Figure 3.1a. The nanorods of permittivity εrod are embedded into a host material with permittivity εmed and are aligned along the z-direction of a Cartesian coordinate system. The nanorod cross section is assumed circular with the semiaxes r directed along the x- and y-coordinate axes, respectively, with a typical inter-rod separation of d. For an homogeneous metamaterial rd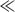 
λ0, with λ0 being the free-space wavelength, and the density of nanorod in the medium N 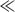1, the local fields in the composite are homogeneous across the rods. Under these conditions the effective permittivities along the nanorod length 
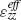and diameter 
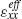can be expressed as [59]
with N = πr2/d2. Thus, the nanorod metamaterial behaves as a uniaxial anisotropic material with the effective permittivity tensor
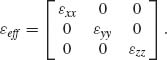
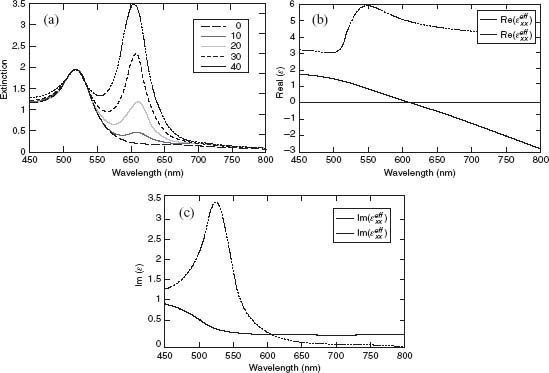
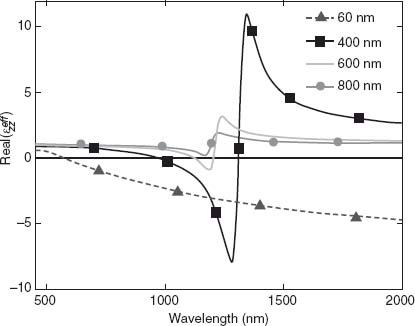
Here, the effective permittivity does not depend on nanorod length but only on nanorod density. On the basis of this model, the calculated extinction for a typical nanorod assembly geometry deposited on a glass substrate is shown in Figure 3.6a. It is calculated using transfer matrix method [60] considering the effective material slab with the thickness equal to the nanorod length. Figures 3.6b and 3.6c show typical effective permittivities that can be calculated from the geometrical and material parameters of the nanorods. The model gives excellent quantitative results for both the spectral position and the amplitude of the resonances. However, in addition to the geometrical domain of validity, the model fails to account for nonlocal effects, which can become measurable when losses in the metal decrease. These nonlocal, spatial dispersion effects are important when electromagnetic fields in the nanorod medium fluctuate in space on the length scales on the order of the spatial variations of the local permittivity. This is discussed in more detail in the next section.
FIGURE 3.6 (a) Extinction spectrum for TM-polarized light calculated using the EMT. The rod length, diameter, and inter-rod distance are 300, 30, and 60 nm, respectively. The embedding medium is AAO. The associated complex-valued effective permittivity along and across the nanorod long axis is plotted in (b) and (c) for the real and imaginary parts, respectively.
The validity domain of the above EMT approach depends significantly on the density of nanorods. In particular it fails to correctly describe the nanorod behavior in the case where the interaction is weak and the optical properties become dependent on the individual nanorod parameters. In this case, EMT can be built from the dipolar response of individual nanorods as has been done by Atkinson et al [29]. In this model, the effective permittivity becomes dependent on the nanorod length. The behavior of the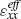 
component is described by a single Lorentzian resonance related to the plasmonic mode associated with the short axis of the nanorods. This resonance red-shifts with decreased inter-rod distance but, more importantly, its strongly localized nature is weakly dependent on nanorod separation. The spectral behavior of 
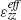is similar for larger inter-rod distances, when near-field interactions between the rods are negligible (kpl > 2π). In this regime the rods are weakly interacting and the nature of the resonance is that of an isolated nanorod embedded in an effective medium made of AAO and neighboring nanorods as shown in Figure 3.7. With an increase in the nanorod concentration, the real part of the effective permittivity becomes negative indicating a metallic behavior of the metamaterial as a whole for light polarized along the nanorods' long axes. The frequency at which 
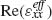changes sign microscopically corresponds to the excitation of the symmetric modes supported by the nanorod assembly with dipoles in adjacent nanorods excited in phase.
FIGURE 3.7 Spectra of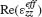 
calculated in the modified Maxwell-Garnet model for assemblies of Au nanorods with different periods.
This regime in the anisotropic metamaterial with diagonal components of the permittivity tensor having opposite signs corresponds to the so-called hyperbolic dispersion regime, and metamaterials with these properties are sometimes called indefinite metamaterials. The consequences of hyperbolic dispersion are very significant for optical properties. In the hyperbolic regime, the metamaterial exhibits very strong Purcell factors leading to significant increase of the spontaneous emission rate due to very high density of the electromagnetic states [35, 61, 62]. In the regime of hyperbolic dispersion, the metamaterial slab behaves as an hyperlens, allowing superfocusing beyond the diffraction limit to be achieved. This is the result of the metamaterial supporting the propagation of electromagnetic modes with very long wavevectors [63].
The effective medium description breaks down and all the above effects smear out when the wavelength of the electromagnetic wave becomes comparable with the distance between the nanorods in the metamaterial. In this regime, the photonic crystal methodology should be applied for accurate description of the optical properties.
3.3.3 Epsilon-Near-Zero Metamaterials and Spatial Dispersion Effects
An ENZ electromagnetic regime occurs when the real part of the permittivity of the material vanishes or approaches zero. In the case of hyperbolic metamaterials, this takes place near the frequency where the transition from hyperbolic to elliptical dispersion regime occurs. In this situation, the real part of 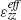is close to zero. In order to describe the optical properties of the material in this ENZ regime, the higher order contributions to the permittivity series, which generally depend on the frequency and wavevector ε(
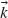, ω), should be taken into account to understand the optical properties of the metamaterial. The lowest order term in the series, which provides a nonzero real part of the permittivity when ε(ω) is zero, depends on the wavevector. The permittivity dependence on the wavevector of the incident radiation leads to nonlocal, spatial dispersion effects. These effects are known from semiconductor physics when they were observed in crystalline solids at ultralow temperatures [64, 65]. Practically, nonlocal effects become important when electromagnetic fields in the nanorod medium fluctuate in space on length scales on the order of the spatial variations of the local permittivity. For nanorod assemblies, nonlocal effects have a sensible impact on the optical properties of the structure already at room temperatures depending on the magnitude of the losses in the metal. In particular, in the optical ENZ regime, spatial dispersion qualitatively changes the optical properties of nanorod assemblies leading to the excitation of additional transverse-magnetic-polarized waves that do not exist in local EMT.
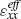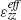In the context of ENZ metamaterials it is convenient to discuss the occurrence of the L-resonance in the spectrum directly in terms of the effective permittivity of the metamaterial. These are plotted in Figures 3.6b and 3.6c where and are the complex permittivities of the nanorod layer across and along the nanorod length, respectively. In this description the L-mode corresponds to 
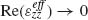. Both the oscillator strength and the width of the L-resonance are limited by losses in material components.
FIGURE 3.8 (a) Schematic of the metamaterial and the optical measurements along with the scanning electron microscopy image of the metamaterial after removal of the anodized aluminum oxide matrix. (b) Spectra of Au permittivity calculated for different values of parameter R. (c and d) Extinction spectra measured with p-polarized incident light for different angles of incidence with the nanorod assemblies (c) unannealed and (d) annealed at 300°C for 2 h. (e and f) Extinction spectra derived from full vectorial 3D simulations for the gold parameters corresponding to R = 5 nm (e) and R = 10 nm (f).
In metamaterials, as well as in crystalline media, spatial dispersion represents in general a relatively weak correction to the effective permittivity εzz(ω) = εzz0(ω) + δε(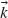) with |δε(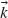)| 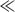1, an effect that can no longer be neglected in the proximity to the ENZ condition where εzz0(ω) = 0. The presence of strong nonlocal terms dramatically changes the optical properties of materials and often leads to the appearance of the additional transverse or longitudinal waves [65].
The nanorod metamaterial layer can support the main wave and an additional transverse magnetic wave [34]. The main wave has a relatively smooth electric field profile and is responsible for the extinction observed in the local regime. In the same frequency range, the additional wave has a strongly nonuniform field distribution and can only weakly couple to incident plane waves. The strong interaction between these modes in the vicinity of the L-resonance leads to a substantial field mixing. As a result of this process, the profiles of both main and additional waves become almost uniform, and both waves contribute to the optical response of the structure, giving rise to two resonances in the optical extinction of the structure. These additional waves, present in most low-loss ENZ metamaterials, represent a new information channel in these systems and therefore may lead to new exciting applications of ENZ metamaterials [34].
These waves can be observed in nanorod metamaterials in the limit of small losses, as the nonlocal spatial dispersion effects are very sensitive to the presence of losses and cannot be detected if the loss is significant. In contrast to thin-film-based plasmonic metamaterials, the nanorods obtained through electrochemical means have poorer Au quality. Thus, the electron motion is limited to a path length on the order of a few nanometers. The effect can be quantitatively described by a restricted mean free path R (R ≤ Rb where Rb = 35.7 nm in bulk gold) of the electrons on the permittivity of gold [34]. For values typical of R, which are on the order of 3 nm, local effects are predominant, and the optical extinction of the metamaterial presents a single L-resonance. However, as R is increased—this is achieved by way of thermal annealing of the nanorods—a splitting in the L-resonance, similar to that of Figure 3.8, is observed [29]. The origin of this splitting is the presence of a second TM-polarized wave supported by the metamaterial. Strong interaction between the two TM waves, signified by the avoided crossing between their dispersion curves, causes the observed doubling of the resonance peak in Figure 3.8 [34].
3.3.4 Guided Modes in the Anisotropic Metamaterial Slab
In addition to the modes discussed above, accessible under the conventional illumination of the metamaterials, the anisotropic metamaterial slab with the effective permittivity tensor described by Equation 3.1 also supports waveguided modes. To access these modes, special illumination conditions are needed, similar to the excitation of waveguided modes in planar dielectric waveguides or surface plasmon polaritons (SPPs). The most interesting case is the waveguided modes in the metamaterial layer, at the frequencies where hyperbolic dispersion is observed.
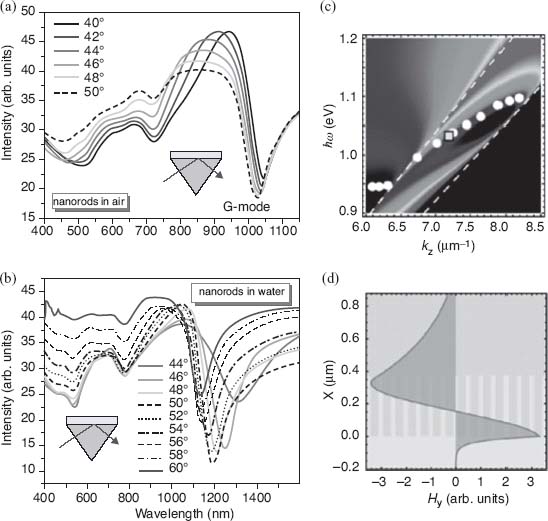
In the attenuated total internal reflection spectrum from the metamaterial layer this waveguided mode is observed as a pronounced minimum together with less pronounced T- and L-resonances of the metamaterial (Fig. 3.9). This mode is only coupled to plane waves with p-polarized light. Similar to the behavior of the T- and L-resonances, for a given frequency, the spectral position of this G-mode depends on the nanorod length, diameter, as well as the refractive index surrounding the nanorods. Its full dispersion is shown in Figure 3.9c. This mode has unique features, being a bulk mode while only existing in the thin subwavelength slab of anisotropic metamaterial. Numerical simulations show that the field associated with this mode is largely concentrated within the metamaterial while also substantially extending in the superstrate as an evanescent wave (Fig. 3.9d). These modes, supported by a metamaterial slab with hyperbolic dispersion, have important applications in refractive index sensing, providing unprecedented sensitivities exceeding 30, 000 nm shifts per unit refractive index change [36].
FIGURE 3.9 Reflection spectra of the metamaterials with the nanorods in (a) air (n = 1) and (b) water environment (n = 1.33) obtained in the ATR geometry with p-polarized light for different angles of incidence. The nanorod parameters are 380 nm length, 25 nm diameter, and 60 nm spacing between the rods (center-to-center). (c) Dispersion of the guided mode in the metamaterial/water system. Background: numerical simulations; circles: experimental dispersion; dashed lines: light lines in air (top left) and the substrate (bottom right). (d) Calculated electromagnetic field distribution of the guided mode in the metamaterial layer. The profile corresponds to the position indicated by the square in (c).
3.4 NONLINEAR EFFECTS IN NANOROD METAMATERIALS
All-optical signal processing is a key requirement for modern photonic technologies to progress toward signal modulation and transmission speeds unsuitable for electronic handling [66]. Practical applications related to all-optical information processing are, however, severely limited by the inherently weak nonlinear effects in conventional materials that govern photon–photon interaction and diminish further as the switching speed increases. The increased photon–photon interaction and, thus, nonlinear optical response of nanostructured systems can be facilitated by the use of plasmonic metals [67]. It provides strong enhancement of the electromagnetic field, crucial for the observation of nonlinear interactions, and enhanced sensitivity to the adjacent dielectric medium and shows a temporal behavior of the optical properties at ultrafast timescales ranging from tens of femtoseconds to a few picoseconds depending on the electron plasma relaxation processes involved [68–70]. These characteristics make plasmonic structures very promising for ultrafast all-optical applications especially at low light intensities.
In this section, we present an overview of the characteristic nonlinear optical properties of nanorod metamaterials. We will start by considering the nonlinearities provided by a nonlinear dielectric incorporated within nanorods. Then, we will discuss the nonlinear effects due to metal nonlinearity, which can be enhanced by appropriate metamaterial design to achieve the ENZ regime. Both the ultrafast time response and the optical nonlinearity are enhanced due to the optically induced modification of the nonlocal behavior of the metamaterial.
3.4.1 Nanorod Metamaterial Hybridized with Nonlinear Dielectric
The electromagnetic field distribution within nanorod metamaterial exhibits significant field localization and enhancement between the nanorods (Fig. 3.4). This field profile originates from the interaction between LSPs of the individual nanorods forming the metamaterial, which in turn depends on the refractive index of the dielectric between the nanorods. This allows designing a nonlinear nanorod metamaterial by embedding nanorods in a polymer matrix demonstrating a Kerr-type nonlinearity [13, 45]. This is a third-order nonlinearity leading to the refractive index changes of the material with the use of a control light intensity:
where ε(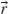
) is the intensity-dependent permittivity of the metamaterial; its spatial dependence is given by the position-dependent field intensity in the metamaterial |
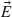(ε(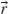), ωpump, 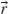)|2. The strength of the change in permittivity is based on the third-order complex-valued susceptibility of the metamaterial at the control light frequency χ(3)(ωpump). It should be emphasized that Equation 3.2 is self-consistent as the permittivity at location 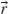is determined by the field at the same location. ε(0)(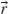) is the position-dependent steady-state permittivity of the metamaterial in the absence of the control light. The advantage of this type of hybrid nonlinear metamaterial is that the local electromagnetic field between nanorods induces changes in the refractive index of the polymer which in turn changes the interaction between the nanorods in the metamaterial resulting in the shift of the metamaterial resonance.
The nonlinear optical response of the nanorod metamaterial hybridized with poly-3BCMU polymer as a nonlinear material exhibits very strong nonlinearity as observed in a pump–probe configuration. A laser light at 515 nm with a 10 ps pulse duration was used as the control light, therefore, interacting with the metamaterial via the transverse plasmonic resonance. A white light continuum was used as a signal beam across the visible spectrum. While the transverse resonance of the metamaterial provides a relatively modest field enhancement compared to the longitudinal resonance, the use of such a control light wavelength is required to induce sensible nonlinearities in the polymer [71, 72].
With increasing control light intensity, the optical response of the nonlinear metamaterial exhibits a complex behavior (Fig. 3.10a) related to an interplay between the effects related to the intensity-dependent changes of the refractive index of the nanorod's surroundings and the structural modifications of the polymer under the control light illumination due to photopolymerization and/or photobleaching. The latter also leads to refractive index changes of the polymer matrix but while the former effect is reversible with respect to the variation of the control light intensity, the latter process is an irreversible change. The resultant effects of the inhomogeneous intensity distribution of the control field and the related spatial distribution of the induced refractive index profile result in a complex asymmetric change in the extinction peak associated with changes in both the real and imaginary parts of the refractive index of the polymer. A broadband nonlinear response, not related to irreversible polymer modifications, is observed in the spectral range from 625 to 800 nm (Fig. 3.10b). The associated tunability range of the L-resonance corresponds to the overall 20 nm wavelength shift with the 10 nm reversible range. The photochromic nonreversible effects in this type of nonlinear metamaterials can be useful for optical data storage applications, while reversible Kerr-type nonlinearities are required for nonlinear photonic applications involving switches and modulators.
FIGURE 3.10 (a) Extinction spectra of the metamaterial with nanorods embedded in a nonlinear polymer after exposure to 515 nm control light of different intensities. (b) The change in the extinction spectrum after irradiation with the 515 nm light plotted from (a). The nanorod length, diameter, and separation are 300, 20, and 40 nm, respectively. The arrows indicate the bleaching of the absorption of the polymer.
3.4.2 Intrinsic Metal Nonlinearity of Nanorod Metamaterials
Metals exhibit intrinsic nonlinearities associated with the free-electron response determining their optical properties. Within the Drude–Lorentz approximation, the optical properties of Au originate from contributions of both free electrons in the conduction band and interband electronic transitions from the d-band to the conduction band [69, 70]. More subtle effects of nonlocality and quantum pressure can be taken into account in rigorous quantum mechanical treatment [73]. Nonlinear effects originate from the modification of the electron temperature and thus redistribution of the electrons in the conduction band [69, 74–76]. This nonlinear effect provides very fast switching times limited by the relaxation of the free electrons [77, 78]. While this type of metal nonlinearities has been studied for smooth metal films, nanoparticles, and nanostructures, including split-ring resonator-based metamaterials [79, 80], the use of nanorod metamaterials exhibiting ENZ regime allows to enhance the nonlinear response [37]. The nonlinearity occurs at the sub-picosecond timescale and with relatively weak peak pump intensity on the order of 10 GW/cm2 resulting in changes in the optical density of up to ΔOD/OD = 0.44, a significant increase over the generally observed values of ΔOD/OD ∼ 0.1 for low-concentration, non-interacting Au nanorods and smooth Au films [81–83].
The linear optical response of the plasmonic nanorod metamaterials used for intrinsic metal nonlinearities studies is shown in Figure 3.11. The transient extinction spectrum ΔOD = –log(TON/TOFF) for the TM-polarized probe light, with TON being the transmission of the sample at a finite delay time τ following excitation by the pump beam and TOFF being the transmission of the sample in the ground state, that is, when τ → ∞, is mapped in Figure 3.12a for an angle of incidence AOI = 20°. Several cross sections of the transient response map are shown in Figure 3.12b as a function of time delay. In Figure 3.12c the angular dependence of the transient spectra is presented for the pump–probe time delay τ = 600 fs. The control light (λ = 465 nm, Δτ = 130 fs) has a peak intensity of about 1 GW/cm2. This is well within the low excitation regime where the pump energy is mostly transferred to the electronic excitations of the rods and then coupled to available electron and phonon modes within the rods and to the dielectric environment [75, 81]. Remarkably, the ΔOD of 0.7 observed at 10 GW/cm2 control intensity corresponds to an 80% change in transmission with a 130 fs pulse-width-limited rise time and a recovery time constant of less than 2 ps.
FIGURE 3.11 Angle-dependent linear extinction of the metamaterial. The rods are embedded in AAO and have an average length, diameter, and center-to-center spacing of 400, 20, and 70 nm, respectively. The illuminating light is TM-polarized.
FIGURE 3.12 (a) Transient extinction map measured for the metamaterial in Figure 3.11 for TM-polarized probe light at an angle of incidence of 20°. The Pump wavelength is 465 nm; the fluence is 0.7 mJ/cm2. (b) Transient extinction spectra at various time delays between pump and probe beams. Spectrum “0 fs” corresponds to the spectrum of the metamaterial measured directly after optical pumping. The other transient spectra correspond to increasing pump–probe time delays τ. (c) Transient extinction spectra at τ = 600 fs measured for different angles of incidence. (d) Numerically modeled transient extinction spectra corresponding to the experimental situation in (c) with an electron temperature increase to 500 K following control light absorption, corresponding to ΔIm(
)/Im() ≈ 0.01; ΔRe()/Re() is negligible far from the interband transition. (e) Transient extinction measured for different pump fluences. (f) Transient extinction calculated for different electron temperatures. In both (e) and (f) the angle of incidence is 40° and the probe light is TM-polarized. Model spectra were calculated without any fitting parameters and do not account for the angular divergence of the probe beam and possible deviations in the angle of incidence.
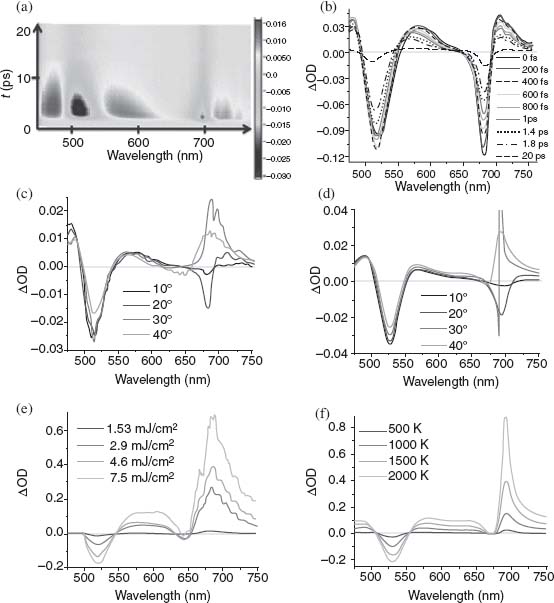
The dynamics of the spectral response observed in Figure 3.12a is specific to the plasmonic resonances of the assembly. While the behavior of the T-resonance is typical of a localized mode for which the plasmon resonance overlaps interband transitions, the behavior of the L-resonance is more complex. As a general trend, this resonance demonstrates a dispersive-type behavior resulting from modifications in the L-resonance width and spectral position, both of which are also typical of isolated plasmonic resonances in the absence of strong damping due to interband scattering [84]. However, while the latter would not show any angular dependency of the dispersive behavior, the L-resonance shows drastic changes in its transient spectral response with AOI as shown in Figure 3.12c. The divergence from the expected behavior occurs for all time delays at an AOI where spectral changes related to nonlocal effects in the metamaterial are most notable (cf. Figs. 3.11 and 3.12c). This AOI dependence of the spectral changes resulting from the nonlocal effects in the metamaterial is reproduced well using both nonlocal effective medium modeling and finite-element numerical calculations. These results are shown in Figure 3.12d where the changes of the dielectric constant of Au were modeled using the Drude–Lorentz model and employing random phase approximation to account for the permittivity changes due to the electron temperature changes under the influence of the control beam. The main contribution to the observed nonlinear response was found to originate from an increased intraband damping constant leading to the modification of both real and imaginary parts of the metal's permittivity, with the increase in Im(Au) being the most significant change in the spectral range of the TM modes. The associated increase in the material's losses results in the modification of the nonlocal optical response of the metamaterial, which is extremely sensitive to the losses in the metal as described above [34].
The T-resonance time response follows a behavior similar to isolated plasmonic resonances supported by subwavelength-size Au particles. It is mainly governed by nonradiative processes with a spectral shape dominated by a transient bleach at around 515 nm surrounded by induced absorption wings (Fig. 3.12b). This peculiar shape is associated with the change in dielectric constant of Au as a function of electron temperature. From the transient spectra of Figure 3.12a, the relaxation dynamics of the T-resonance is governed by two relaxation channels corresponding to electron–phonon and phonon–phonon scattering: γT-mode = 1/τT-mode = 1/τe–ph + 1/τph–ph where τe–ph = 1.6 ± 0.05 ps and τph–ph = 115 ± 0.1 ps, respectively.
The dynamics of the L-resonance displays a similar behavior with most of the energy dissipated within the picosecond timescale where e–e scattering and ph–ph scattering events are not predominant relaxation pathways. However, compared to the T-resonance, the L-resonance demonstrates an enhanced relaxation rate with γL-mode > γT-mode, unexpected for a plasmonic mode in this spectral range. Indeed, considering the spectral position of the L-resonance around 1.8 eV (690 nm), well below the interband transition threshold of 2.4 eV, no contributions from those transitions are expected in the picosecond timescale. The dynamics of the L-resonance in the picosecond range must, therefore, comprise an additional relaxation channel identified as the waveguided mode and can be expressed as τL-mode = (γL-mode)–1 = (γe–ph + γWg.)−1 [34]. τL-mode was obtained from the spectra in Figure 3.2a for wavelengths spanning the resonance width. τL-mode values ranging from 0.76 ± 0.05 to 1.13 ± 0.05 ps were measured for different wavelengths around the resonance, resulting in a nonuniform modification of the resonance shape with delay time. A reduction in pump fluence to 0.7 mJ/cm2 leads to a faster ∼700 fs relaxation time due to a smaller increase of the electron temperature.
With their unusually strong intrinsic nonlinear optical response, nanorod metamaterials provide a new class of optical media for ultrafast strongly nonlinear processes, with numerous applications in optical communications, extraordinarily sensitive optical spectroscopies, and subwavelength imaging technologies. Coupled plasmonic nanoparticles have also been proposed as a means to propagate energy through linear chains of closely coupled nanoparticle chains, while still maintaining subwavelength lateral width. In this context, the nonlinear response of the delocalized L-resonance may provide ground for the comprehensive design of the next-generation nanophotonic circuitry. In all these applications the ability to switch and modulate optical properties, or indeed tune the properties of the nanostructures with the control optical beam, is of great importance.
3.5 MOLECULAR PLASMONICS IN METAMATERIALS
Controlling coherent electromagnetic interactions in molecular systems is a problem of both fundamental interest and important applicative potential in the development of photonic and optoelectronic devices. The strength of these interactions determines both the absorption and emission properties of molecules hybridized with nanostructures, effectively governing the optical properties of such a composite metamaterial. Here, we discuss strong coupling between a plasmonic mode of metamaterial and a molecular exciton. The coupling can be easily engineered and is deterministic as both spatial and spectral overlaps between the plasmonic structure and molecular aggregates are controlled [47]. These results, in conjunction with the flexible geometry of the assembly of gold nanorods, are of potential significance to the development of plasmonic molecular devices.
J-aggregates support excitonic states corresponding to electrically neutral electrons/holes pairs created by the absorption of photons. In photosynthetic processes, these states are used by plants to collect, store, and guide energy to the reaction center for energy conversion and could therefore drive artificial devices on identical principles. Excitonic states also show very strong nonlinear optical behavior that could be used to produce stimulated sources of photons and transistor-like action. Their coupling with plasmons appears as a particularly attractive approach to creating low-powered optical devices having demonstrated the possibility of using the strong scattering cross section and associated enhanced field concentrations of plasmons to generate stimulated emission of excitons of J-aggregates with very low excitation powers [85]. In addition, the coupling of J-aggregates to plasmons-supporting geometries presents genuine fundamental interest in the creation of mixed plasmon/exciton states [85–87]. These quasiparticles can be created if the energy of the excitonic mode is resonant with a plasmonic transition. Either weak or strong coupling can then be achieved depending on whether the transition probabilities associated to the system's eigenmodes are still governed by the Fermi golden rule. Tuning the coupling strength is therefore of particular interest to tailor the absorption and emission characteristics of the molecular semiconductor. Strong coupling was observed in different systems including microcavities where the quasiparticle comprises a cavity photon and a molecular exciton [88, 89] in plasmonic systems involving an SPP and a waveguide photon[90], and more recently between an SPP and an exciton [86, 91]. The flexible geometry of the nanorod metamaterial can be used to control the positioning of J-aggregates in the plasmonic structure as well as control the mixing of the hybrid system's eigenstates, offering a unique possibility in the designing of molecular plasmonic nanodevices with tailored optoelectronic functionalities.
The extinction spectra for both the assembly of nanorods and the J-aggregate when formed on a smooth Au film are shown in Figure 3.13. The metamaterial mode spectrum is dominated by the T- and L-resonances at 500 and 750 nm as discussed earlier. Because of the peculiar electric field distribution of the L-mode showing a maximum in the inter-rod spacing rather than around the rods' extremity, coupling of the excitonic state from the molecular aggregate to either or both the plasmonic modes of the assembly then requires creating a shell around the rods in which to introduce the dye. This opens up unique opportunities to controllably couple plasmonic structures with their environment. Indeed, the thickness of the shell represents an additional geometrical parameter allowing one to tune the optical properties of the plasmonic structure over the [500–900] nm range, while it simultaneously offers spatial selectivity to couple the plasmonic resonances with active molecules. Figures 3.14a and 3.14b show the extinction of the coupled system for two different shell thicknesses of 2.5 and 20 nm, respectively. Varying the shell thickness effectively tunes the plasmonic resonances with no measurable effect on the excitonic transition energy located around the wavelength of 622 nm. The shell thickness therefore can be used to control the spectral overlap between the plasmonic modes of the assembly of nanorods and the excitonic state of the J-aggregate.
FIGURE 3.13 Extinction spectrum of the metamaterial with Au nanorods in AAO as a function of angle of incidence. The inset shows the molecular structure of the dye used to hybridize the metamaterial along with its extinction spectrum when J-aggregated on a 50 nm thick smooth Au film magnetron sputtered on a glass substrate. The rod's diameter, spacing, and length are 16, 50, and 250 nm, respectively.
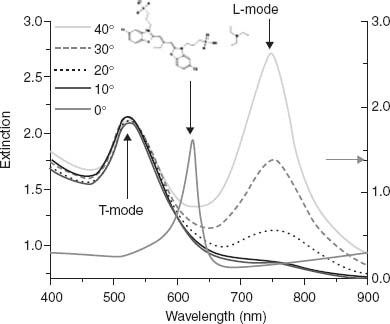
FIGURE 3.14 (a) Extinction spectrum of the active metamaterial with incorporated dye in the weak plasmon–exciton coupling regime along with the extinction of the metamaterial before dye incorporation and the extinction of the J-aggregate on an Au film. The shell thickness is 2.5 nm. (b) Extinction spectrum of the active metamaterial in the strong plasmon–exciton coupling regime along with the extinction of the passive metamaterial and the extinction of the J-aggregate on an Au film. The shell thickness is 20 nm. The spectra are taken for an angle of incidence of 40°. (c) TEM cross section of the core–shell structure and its schematics. The arrow shows the orientation of the molecular transition dipole moment with respect to the long axis of the Au nanorod when introduced in the shell. (d) Extinction from a coated Au ellipsoid calculated in the dipolar limit, illustrating the general behavior observed experimentally in (a) and (b). The thin lines correspond to the individual systems, while the thick lines describe the response of the hybrid system.
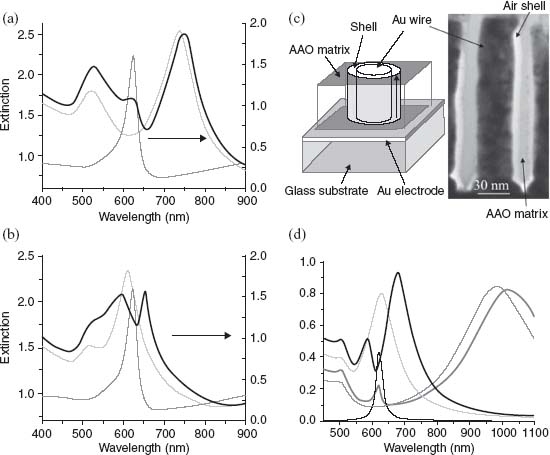
From Figure 3.14a it can be seen that when the overlap between the L-resonance (λL = 737 nm) and the excitonic transition (λJAgg = 622 nm) is small, then the spectral response of the extinction associated to the hybrid system (λhybrid+ = 745 nm, λhybrid– = 622 nm) is essentially determined by the resonances of the isolated systems, that is, weak coupling is observed. Conversely, Figure 3.14b illustrates the regime where this overlap is strong (λL = 610 nm, λJAgg = 622 nm). The resonances of the hybrid system (λhybrid+ = 654 nm and λhybrid– = 593 nm) then reflect the hybridization of the original resonances into mixed states with shared plasmon/exciton character, that is, strong coupling is observed.
The general behavior observed in Figures 3.14a and 3.14b can be illustrated following the procedure described in Reference 87 and calculating the extinction cross section for isolated ellipsoidal nanoparticles with an Au core surrounded by an excitonic shell and embedded in a homogeneous medium of dielectric constant d [86]. This quantity can be expressed as
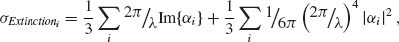
where λ is the wavelength in vacuum and αi the dipolar polarizability of the core–shell ellipsoid along axis i expressed in the electrostatic approximation [92]. The dielectric constant d of the embedding medium alumina is taken to be 2.56 while a polynomial fit of the data published in Reference 92 is used to describe the dielectric constant of Au, Au. The response of the shell was modeled by an excitonic resonance with a Lorentzian response in a dielectric background ∞. The anisotropy of the exciton's transition dipole moment was approximated by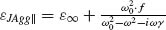 
and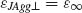 
, for the contributions along and perpendicular to the aggregate's transition dipole moment, respectively. The high-frequency dielectric constant ∞ was extracted from ellipsometric measurement made on a thin J-aggregate film formed on a smooth Au surface, while the transition energy, reduced oscillator strength, and damping of the excitonic state were determined by fitting the J-aggregate's absorption spectrum as measured on the smooth Au film in Figure 3.13. These parameters then take the respective values of ∞ = 1.21, ħω0 = 1.99 eV (λ = 622 nm), f = 0.054, and ħγ = 66 meV. Figure 3.14d shows the calculated extinction cross section for core–shell ellipsoids with aspect ratios of 2.4 and 6 with a constant shell thickness of 2 nm. The thick lines correspond to the coupled plasmon/exciton system while the thin lines describe the extinction of the Au ellipsoids but surrounded by an air shell. The extinction of the J-aggregate is also shown. The aspect ratio of the ellipsoid was parameterized to modify the spectral overlap between the long-axis plasmonic resonance of the ellipsoid and the transition energy of the exciton, and therefore the coupling strength between the two transition dipole moments. In Figure 3.14d, only the long-axis plasmonic mode was coupled to the excitonic transition, reflecting the experimental observations. In a situation where both transverse and longitudinal modes from the ellipsoid were to be coupled with the excitonic transition, four modes would be observed in the hybrid's extinction spectrum: two transverse modes as well as two longitudinal modes.
In order to gain a better insight into the coupling mechanism let us consider a three-dimensional physical system whose Hamiltonian is H0. The eigenstates of H0 are |
T>, |L>, and |JAgg> associated to the rods' dipolar transverse plasmonic resonance, the ANR's longitudinal resonance, and the J-aggregate excitonic state. The corresponding eigenvalues are ET, EL, and EJAgg satisfying H0|T> = ET|T>, H0|L> = EL|L>, and H0|JAgg> = EJAgg|JAgg>, with <i|j> = δij. Introducing coupling between these levels and searching for the eigenvalues of the coupled system in the {|T>, |L>, |JAgg>} basis, we rewrite the Hamiltonian H = H0 + V, where V is a time-independent perturbation accounting for the coupling between the different eigenstates of the isolated system. Assuming that the J-aggregate's transition dipole moment is oriented along the long axis of the nanorods only, the Hamiltonian takes the following simplified form, where Vhybrid couples |L> and |JAgg>:
(3.3)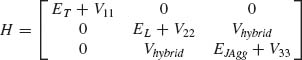 
from which the eigenvalues are readily obtained:
(3.4)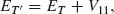 
where E'L = EL + V22 and E'JAgg = EJAgg + V33.
The eigenvector associated with E'T is |ψT> ∼ |T> reflecting the fact that the J-aggregate's transition dipole moment and the T-mode were taken to be perpendicular to each other in our expression of the coupling Hamiltonian V. Consequently, for the transverse mode in the hybrid structure, the presence of the J-aggregate along the Au nanorod results in a net change in the energy E'T through a change in the dielectric constant in the shell, with an eigenvector that is essentially unchanged from its original dipolar form. Neglecting the core–shell geometry as well as the presence of the substrate, an approximate expression for V11 can be found by assuming a loss-less Drude-like dielectric response of the form ε(ω) = 1 − ωp2/ω2 for an Au ellipsoid embedded in a homogeneous medium of effective dielectric constant eff:
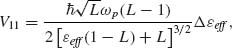
where ωp is the bulk plasma frequency of Au, L is the geometric factor defined earlier, and Δeff reflects the change in dielectric constant induced by the introduction of the J-aggregate in the shell. V11 is an increasing function of the shell thickness through Δeff with an upper value of V11 ∼ –20 meV measured for a complete removal of the AAO matrix (Δeff ∼ air − εJAgg⊥ = −0.21). The negative value of V11 reflects the increase in the index of refraction of the shell when introducing the molecule. Similar to V11, V22 reflects the change in the L-resonance position upon J-aggregation in the shell via the off-resonance high-frequency dielectric constant of the J-aggregate. However, V22 is more difficult to express analytically since the field associated to the L-mode within the assembly of nanorods is no longer following the dipolar response of the isolated rod's long-axis resonance. An estimated value of V22 can be made by measuring the sensitivity of the L-resonance as a function of shell thickness for the index of refraction in the shell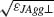 
of 1.1. This allows us to evaluate the variation ΔV22 of V22 over the shell thickness range considered in this study of about 65 meV while V22 at 736 nm is about –20 meV and ΔEL is about 570 meV. V33 is the measure of the variation of the intermolecular coupling J within the aggregate when it adsorbs on the Au nanorods with respect to a reference state measured in water: E'JAgg = EJAgg + V33. The loss in potential energy of the highest occupied molecular orbital (HOMO) upon J-aggregation determines the coupling energy J which can then be defined from the transition energy ΔEJAgg of the aggregate as 2J = ΔE – ΔEJAgg, where ΔE is the transition energy of the monomer and J is the positive coupling energy. To evaluate V33, J-aggregation has been studied on a smooth Au film, a borosilicate glass substrate, and a porous AAO from a dye solution in methanol. For all those situations the excitonic transition was observed at an identical wavelength of 622 nm, slightly blue-shifted from its value in water. This underlines that in the experimental configurations considered it is the interfacial geometry that governs the aggregation energy rather than the material properties of the substrate itself. Comparing Figure 3.13 with Figure 3.14a it is deduced that J-aggregation in the shell around the rods leads to an intermolecular coupling energy similar to the one measured on planar interfaces suggesting that the core–shell geometry does not strongly affect the value of J in the aggregate even for the smallest shell thicknesses studied (∼2 nm). Consequently, the value of V33 is assumed to be shell thickness independent in the following. Considering the absorption frequency of the J-aggregate in both water (λ = 650 nm, i.e., 2J = 230 meV) and when adsorbed on Au nanorods (λ = 622 nm, i.e., 2J = 150 meV) we can deduce that V33 = E'JAgg − EJAgg = ΔE – 2J′ – (ΔE – 2J) = 80 meV.
The eigenvectors |ψ+> and |ψ–>, associated to, respectively, Ehybrid+ and Ehybrid–, can be expressed as linear combinations of the longitudinal plasmonic orbital |L> and the J-aggregate excitonic orbital |JAgg> as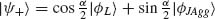 
and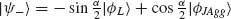 
, where 
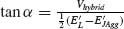. The effect of the coupling matrix V on H0 is to hybridize the longitudinal and excitonic states into two new eigenstates with a mixed plasmon–exciton character. It follows that if |E'L − E'JAgg| 
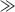2Vhybrid, then α ∼ 0, cos α/2 ∼ 1, and sin α/2 ∼ Vhybrid/|E'T − E'JAgg|, from which, if we assume in this instance that E'L > E'JAgg, we deduce the wavefunctions of the system as 
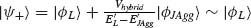and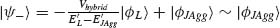 
. These hybrid orbitals then resemble the plasmonic and excitonic orbitals from the uncoupled system in which case these orbitals represent a weakly coupled system as they retain their original character. This case is illustrated in Figure 3.14a for E'JAgg > E'L. Similarly, if we now consider the case for which |E'L − E'JAgg| 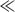2Vhybrid, then 
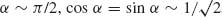, and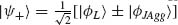 
. These functions are hybrid orbitals of the system of Figure 3.14b where the two original uncoupled orbitals overlap spectrally in which case strong coupling is achieved.
The unique characteristic of the core–shell nanorod geometry enables a continuous tuning of the plasmonic resonances by controlling the thickness of the shell created around the rods. The spectral position of the L-resonance can, therefore, be scanned through most of the visible spectrum and across the excitonic resonance to modulate the mixing of these states. The result is shown in Figure 3.15 where the spectrum of the hybrid assembly of nanorods is plotted for different positions of the L-resonance in air.
FIGURE 3.15 Extinction from the hybridized metamaterial with varying coupling strength between the plasmonic L-mode and the molecular excitonic transition. The spectra are taken at an angle of incidence of 40°. The plasmon–exciton coupling strength has been adjusted by tuning the spectral position of the L-resonance from 736 to 550 nm by increasing the thickness of the shell around the Au rods. The L-resonance position in air is shown for hybrids at 736 nm (2.5 nm), 733 nm (3.8 nm), 716 nm (5.6 nm), 700 nm (7.7 nm), 650 nm (8.9 nm), 600 nm (20 nm), and 550 nm (no shell, matrix completely removed). The black broken line shows the excitonic extinction on a 50 nm thick smooth Au film.
The occurrence of the strong coupling regime in the structure is evident since no resonances appear in the spectral range from 622 to 658 nm while the L-resonance resonance was continuously tuned from 736 to 550 nm. The anticrossing between the L-resonance and the excitonic transition is illustrated in Figure 3.16a. Deriving Vhybrid from Equations 3.5 and 3.6, we use Figure 3.15 to estimate the coupling strength within the hybrid as a function of the overlap between the L-resonance and the excitonic states as
where the assumption E'L ∼ EL was made. The result is plotted in Figure 3.16 as a function of the original position of the L-resonance. A similar relationship derived from an analytical theory for the optical properties of ellipsoidal plasmonic particles covered by anisotropic molecular layers leads to very similar values for Vhybrid as a function of the L-resonance wavelength with a small overestimation of the coupling strength when using Equation 3.7. This overestimation reflects the effect V22 has on E'L: The absolute value of V22 increases with shell thickness and is negligible at maximum coupling strength. This maximum is reached for an L-resonance in air located at 600 nm and corresponds to a Rabi splitting of 155 meV. This value is commensurate with the largest Rabi splitting observed in planar organic microcavities [93] and similar to recent observations for an excitonic state mixed with a planar SPP [94].
FIGURE 3.16 (a) Energy diagram showing the anticrossing of the plasmonic (diagonal solid black line) and the excitonic (horizontal dotted black line). The energy branches of the hybrid system are plotted based on Figure 3.15. The crossing of the high-energy branch and the plasmon line is due to V22 upon hybridization (see text for details). The size of the square markers represents the error bars. (b) Coupling strength calculated from Equation 3.6. The data are represented by circular dots, and the solid line is a guide for the eye. For comparison, the black square dots are obtained using the formula for the coupling strength as derived in Reference 47. The dotted line is a guide for the eye.
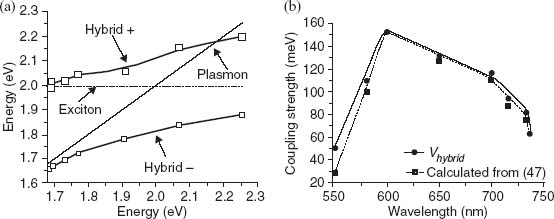
The ability to control the coupling strength between a metamaterial mode and a molecular exciton both spatially and spectrally is a major step toward implementing active and passive plasmonic devices. Based on the hybrid nature of the coupled states, the nonlinear optical properties of such metamaterial should demonstrate extreme sensitivity over a large spectral range; that is, by addressing one of the hybrid resonances one would effectively affect both coupled resonances and therefore affect the extinction of the device from 550 to 700 nm. This could be achieved optically in a pump–probe configuration, for example, and possibly also electrically by dynamically controlling the orientation/ordering of the molecular aggregate. Because of the coupled nature between plasmonic and excitonic states, future investigations on the emission properties of this hybrid structure should stimulate considerable interest as well [87].
3.6 ELECTRO-OPTICAL EFFECTS IN PLASMONIC NANOROD METAMATERIAL HYBRIDIZED WITH LIQUID CRYSTALS
Finally we will describe how the transmission through the metamaterial can be controlled electronically upon hybridization of the metamaterial with an electro-optic medium such as liquid crystals (LC) [12]. Plasmonic devices with electric field-tuneable resonances have been demonstrated for both plasmonic crystals and plasmonic waveguide-based devices [95–98]. In all these cases, the effect relies on the modification of the refractive index when the LC orientation is changed upon applied external electric field and the associated shift in the resonance position of the Bloch mode or waveguided mode.
In contrast, when the nanorod metamaterial is placed in proximity to the LC layer, reorientation of anisotropic molecules does not provide spectral tunability of the metamaterial resonances due to their field distribution: The field is concentrated inside the AAO matrix and is not sensitive to the refractive index changes of the superstrate. Nevertheless, polarization effects associated with the LC reorientation in external electric field combined with the polarization properties of the anisotropic metamaterials can be used for light switching and modulation applications [12].
Figure 3.17 shows the effect of the LC and electric applied field on the extinction spectra of the metamaterial. When the LC is present near the metamaterial, it completely extinguishes the L-resonance at 712 nm if no electric field is applied. The application of a small field leads to an initial increase in the extinction of the T-resonance and a decrease in the extinction at the L-mode amplitude. As the voltage is further increased, the extinction of the T-resonance decreases while the L-resonance starts to appear which then rapidly increases. A steady increase in the L-resonance amplitude with increasing applied voltage is observed up to saturation. This process is completely reversible and shows good reproducibility as the applied field is removed. This effect is observed for illumination through the LC side. When the device is illuminated through the metamaterial, the L-resonance extinction is unchanged by the presence of the LC independently of the applied field. The observations of both electric field-dependent extinction and nonreciprocity with respect to the illumination side suggest that the polarization effects determined the observed electro-optical switching. The LC layer conformation has molecules oriented in the plane of the substrate (perpendicularly to the nanorod axes) when no electric field is applied. The TM-polarized incident light is then converted into TE-polarized light when transmitted through the LC molecules layer. In the configuration where light transmits first through the LC layer before interacting with the nanorod layer, the L-resonance cannot be excited and is not present in the extinction of the sample. Applying the voltage causes the LCs to orient along the field, that is, perpendicular to the substrate and along the direction of the nanorod long axes. In this orientation they no longer affect the polarization of the incident TM-polarized light and hence the L-resonance is observed again.
FIGURE 3.17 (a) Extinction spectra of the metamaterial (20 nm diameter, 400 nm long gold nanorods embedded in AAO) with a 100 mm top liquid crystal layer as a function of applied electric field. The incident light is TM-polarized and the angle of incidence is 40°. (b) Dependence of the metamaterial extinction at 715 nm as a function of applied electric field.
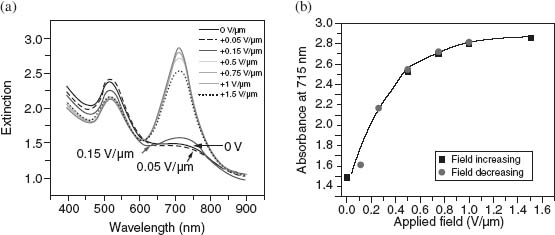
Comparing with previous work on gold nanorods [96], nanoparticles [97], and nanodots [98], it can be seen that the nanorod metamaterial allows observing much larger changes in the extinction spectra for smaller applied electric fields, and this without the need for a rubbing layer, but it does not provide tunability of the plasmonic resonances.
3.7 CONCLUSION
We have presented an overview of the optical properties of plasmonic nanorod metamaterials with an emphasis on their applications in active nanophotonics. In particular, we have focused on their nonlinear optical properties and ultrafast all-optical switching, electro-optical switching in LC-infiltrated metamaterials, and strong plasmon–exciton coupling effects. The use of metamaterials with both nonlinear and electro-optical effects allows one to achieve enhanced functionalities and design the required operation wavelengths by tuning the geometry of the nanorod assembly forming the metamaterial. The influence of the refractive index changes provided by the external stimuli not only leads to the modification of the LSP resonances associated with individual nanorods but also influences the plasmonic interaction between nanorods in the metamaterial, providing the improved functionalities of metamaterial compared to individual nanorods.
In addition to the above-discussed active functionalities, this type of anisotropic metamaterial with hyperbolic dispersion has the unique potential for influencing quantum effects such as spontaneous emission due to extremely strong Purcell effect related to the hyperbolic dispersion and can be used to control the properties of quantum emitters [35, 62]. The high-resolution imaging capabilities of this type of metamaterial related to hyperbolic dispersion have also been demonstrated [63]. The nanorod metamaterial has a record figure of merit for sensing, relying on the strong sensitivity of its resonant response to the plasmonic interaction between nanorods and, thus, on the refractive index of the analyte between nanorods [36, 99]. The ability to use different materials for building the nanorod metamaterial has been applied for designing novel ferromagnetic properties using assemblies of Ni and Co nanorods. Magnetic nanorod metamaterial exhibits peculiar magnetic properties as well as magneto-optical response with the prominent role of spin-waves in magnetic nanorods [100].
Further extension of the anisotropic metamaterial designs has been very recently demonstrated by replacing nanorods by plasmonic nanotubes. This type of nanostructures provides access to a wider range of plasmonic modes, which can be used for further designing optical properties [101]. This can be advantageous for both biosensing and nonlinear optical functionalities [102].
REFERENCES
1. Cai W, Shalaev VM (2009) Optical Metamaterials: Fundamentals and Applications. New York: Springer.
2. Zheludev NI (2010) The road ahead for metamaterials. Science 328: 582.
3. Soukoulis CM, Wegener M (2011) Past achievements and future challenges in the development of three-dimensional photonic metamaterials. Nat. Photonics 5: 523.
4. Smith DR, Pendry JB, and Wiltshire MCK (2004) Metamaterials and negative refractive index. Science 305: 788.
5. Tsakmakidis KL, Boardman AD, and Hess O (2007) ‘Trapped rainbow’ storage of light in metamaterials. Nature (Lond.) 450: 397.
6. Cai W, Chettiar UK, Kildishev AV, Shalaev VM (2007) Optical cloaking with metamaterials. Nat. Photonics 1: 224.
7. Ma H-F and Cui TJ (2010) Three-dimensional broadband ground-plane cloak made of metamaterials. Nat. Commun. 1: 1.
8. Gharghi M, Gladden C, Zentgraf T, Liu Y, Yin X, Valentine J, and Zhang X (2011) A carpet cloak for visible light. Nano Lett. 11: 2825.
9. Hoffman AJ, Alekseyev L, Howard SS, Franz KJ, Wasserman D, Podolskiy VA, Narimanov EE, Sivco DL, and Gmachl C (2007) Negative refraction in semiconductor metamaterials. Nat. Mater. 6: 946.
10. Zhang X and Liu Z (2008) Superlenses to overcome the diffraction limit. Nat. Mater. 7: 435.
11. Kundtz N and Smith DR (2010) Extreme-angle broadband metamaterial lens. Nat. Mater. 9: 129.
12. Evans PR, Wurtz GA, Hendren WR, Atkinson R, Dickson W, Zayats AV, and Pollard RJ (2007) Electrically switchable nonreciprocal transmission of plasmonic nanorods with liquid crystal. Appl. Phys. Lett. 91: 043101.
13. Dickson W, Evans P, Wurtz GA, Hendren W, Atkinson R, Pollard RJ, and Zayats AV (2008) Towards nonlinear plasmonic devices based on metallic nanorods. J. Microsc. 420: 415.
14. Lu Y, Rhee JY, Jang WH, and Lee YP (2010) Active manipulation of plasmonic electromagnetically-induced transparency based on magnetic plasmon resonance. Opt. Express 18: 20912.
15. Kang L, Zhao Q, Zhao H, and Zhou J (2008) Magnetically tuneable negative permeability metamaterial composed by split ring resonators and ferrite rods. Opt. Express 16: 8825.
16. Jun YC, Gonzales E, Reno JL, Shaner EA, Gabbay A, and Brener I (2012) Active tuning of mid-infrared metamaterials by electrical control of carrier densities. Opt. Express 20: 1903.
17. Lee SH, Choi M, Kim T-T, Lee S, Liu M, Yin X, Choi HK, Lee SS, Choi C-G, Choi S-Y, Zhang X, and Min B (2012) Switching terahertz waves with gate-controlled active graphene metamaterials. Nat. Mater. 11: 1476.
18. Friedman RS, McAlpine MC, Ricketts DS, Ham D, and Lieber CM (2005) High-speed integrated nanowire circuits. Nature 434: 1085.
19. Tong LM, Gattass RR, Ashcom JB, He SL, Lou JY, Shen MY, Maxwell I, and Mazur E (2003) Subwavelength-diameter silica wires for low-loss optical wave guiding. Nature 426: 816.
20. Xiang J, Lu W, Hu Y, Wu Y, Yan H, and Lieber CM (2006) Ge/Si nanowire heterostructures as high-performance field-effect transistors. Nature 441: 489.
21. Gudiksen MS, Lauhon LJ, Wang J, Smith DC, and Lieber CM (2002) Growth of nanowire superlattice structures for nanoscale photonics and electronics. Nature 415: 617.
22. Krenn JR, Lamprecht B, Ditlbacher H, Schider G, Salerno M, Leitner A, Aussenegg FR (2002) Nondiffraction-limited light transport by gold nanowires. Europhys. Lett. 60: 663.
23. Mühlschlegel P, Eisler H-J, Hecht B, and Pohl DW (2005) Resonant optical antennas. Science 308: 1607.
24. Shalaev VM, Cai WS, Chettiar UK, Yuan Hk, Sarychev AK, Drachev VP, and Kildishev AV (2005) Negative index of refraction in optical metamaterials. Opt. Lett. 30: 3356.
25. Evans P, Hendren WR, Atkinson R, Wurtz GA, Dickson W, Zayats AV, and Pollard RJ (2006) Growth and properties of gold and nickel nanorods in thin film alumina. Nanotechnology 17: 5746.
26. Lee K-S and El-Sayed MA (2006) Gold and silver nanoparticles in sensing and imaging: sensitivity of plasmon response to size, shape, and metal composition. J. Phys. Chem. B 110: 19220.
27. Pelton M, Liu M, Park S, Scherer NF, and Guyot-Sionnest P (2006) Ultrafast resonant optical scattering from single gold nanorods: large nonlinearities and plasmon saturation. Phys. Rev. B 73: 155419.
28. Schider G, Krenn JR, Hohenau A, Ditlbacher H, Leitner A, Aussenegg FR, Schaich WL, Puscasu I, Monacelli B, and Boreman G (2003) Plasmon dispersion relation of Au and Ag nanowires. Phys. Rev. B 68: 155427.
29. Atkinson R, Hendren WR, Wurtz GA, Dickson W, Zayats AV, Evans P, and Pollard RJ (2006) Anisotropic optical properties of arrays of gold nanorods embedded in alumina. Phys. Rev. B 73: 235402.
30. Ono A, Kato J-i, and Kawata S (2005) Subwavelength optical imaging through a metallic nanorod array. Phys. Rev. Lett. 95: 265407.
31. Podolskiy VA, Sarychev AK, Narimanov EE, and Shalaev VM (2005) Resonant light interaction with plasmonic nanowire systems. J. Opt. A Pure Appl. Opt. 7: S32.
32. Rahachou AI and Zozulenko IV (2007) Light propagation in nanorod arrays. J. Opt. A Pure Appl. Opt. 9: 265.
33. Rahman A, Kosulnikov SY, Hao Y, Parini C, Belov PA (2011) Subwavelength optical imaging with an array of silver nanorods. J. Nanophoton. 5: 051601.
34. Pollard RJ, Murphy A, Hendren WR, Evans PR, Atkinson R, Wurtz GA, Zayats AV, and Podolskiy VA (2009) Optical nonlocalities and additional waves in epsilon-near-zero metamaterials. Phys. Rev. Lett. 102: 127405.
35. Poddubny AN, Belov PA, Ginzburg P, Zayats AV, and Kivshar YS (2012) Microscopic model of Purcell enhancement in hyperbolic metamaterials. Phys. Rev. B 86: 035148/1.
36. Kabashin AV, Evans P, Pastkovsky S, Hendren W, Wurtz GA, Atkinson R, Pollard R, Podolskiy VA, and Zayats AV (2009) Plasmonic nanorod metamaterials for biosensing. Nat. Mater. 8: 867.
37. Wurtz GA, Pollard R, Hendren W, Wiederrecht G, Gosztola D, Podolskiy VA, and Zayats AV (2011) Designed ultrafast optical nonlinearity in a plasmonic nanorod metamaterial enhanced by nonlocality. Nat. Nanotechnol. 6: 107.
38. Liu NW, Datta A, Liu CY, Peng CY, Wang HH, and Wang YL (2005) Fabrication of anodic-alumina films with custom-designed arrays of nanochannels. Adv. Mater. 17: 222.
39. Liu N-W, Liu C-Y, Wang H-H, Hsu C-F, Lai M-Y, Chuang T-H, and Wang Y-L (2008) Focused-ion-beam-based selective closing and opening of anodic alumina nanochannels for the growth of nanowire arrays comprising multiple elements. Adv. Mater. 20: 2547.
40. Kustandi TS, Loh WW, Gao H, and Low HY (2010) Wafer-scale near-perfect ordered porous alumina on substrates by step and flash imprint lithography. ACS Nano 4: 2561.
41. Wolfrum B, Mourzina Y, Mayer D, Schwaab D, and Offenhusser A (2006) Fabrication of large-scale patterned gold-nanopillar arrays on a silicon substrate using imprinted porous alumina templates. Small 2: 1256.
42. Reinhardt C, Passinger S, Chichkov BN, Dickson W, Wurtz GA, Evans P, Pollard R, Zayats AV (2006) Restructuring and modification of metallic nanorod arrays using femtosecond laser direct writing. Appl. Phys. Lett. 89: 231117.
43. Lillo M, Losic D (2009) Ion-beam pore opening of porous anodic alumina: the formation of single nanopore and nanopore arrays. Mater. Lett. 63: 457.
44. Wurtz GA, Dickson W, O'Connor D, Atkinson R, Hendren W, Evans P, Pollard R, Zayats AV (2008) Guided plasmonic modes in nanorod assemblies: strong electromagnetic coupling regime. Opt. Express 16: 7460.
45. Dickson W, Wurtz, GA, Evans P, O'Connor D, Atkinson R, Pollard R, Zayats AV (2007) Dielectric-loaded plasmonic nano-antenna arrays: a metamaterial with tuneable optical properties. Phys. Rev. B 76: 115411.
46. Evans PR, Wurtz GA, Atkinson R, Hendren W, O'Connor D, Dickson W, Pollard RJ, and Zayats AV (2007) Plasmonic core/shell nanorod arrays: subattoliter controlled geometry and tuneable optical properties. J. Phys. Chem. C 111: 12522.
47. Wurtz GA, Evans PR, Hendren W, Atkinson R, Dickson W, Pollard RJ, Harrison W, Bower C, and Zayats AV (2007) Molecular plasmonics with tuneable exciton-plasmon coupling strength in J-aggregate hybridized Au nanorod assemblies. Nano Lett. 7: 1297.
48. Maier SA, Kik PG, Atwater HA, Meltzer S, Requicha A, and Koel BE (2002) Observation of coupled plasmon-polariton modes of plasmon waveguides for electromagnetic energy transport below the diffraction limit. Proc. SPIE 4810.
49. Maier SA, Kik PG, and Atwater HA (2003) Optical pulse propagation in metal nanoparticle chain waveguides. Phys. Rev. B 67: 205402.
50. Park SY and Stroud D (2004) Surface-plasmon dispersion relations in chains of metallic nanoparticles: an exact quasistatic calculation. Phys. Rev. B 69: 125418.
51. Jain PK, Eustis S, El-Sayed MA (2006) Plasmon coupling in nanorod assemblies: optical absorption, discrete dipole approximation simulation, and exciton-coupling model. J. Phys. Chem. B 110: 18243.
52. Rechberger W, et al. (2003) Optical properties of two interacting gold nanoparticles. Opt. Commun. 220: 137.
53. Koenderink AF and Polman A (2006) Complex response and polariton-like dispersion splitting in periodic metal nanoparticle chains. Phys. Rev. B 74: 033402.
54. Vlad A, Matefi-Tempfli M, Faniel S, Bayot V, Melinte S, Piraux L, and Matefi-Tempfli S (2006) Controlled growth of single nanowires within a supported alumina template. Nanotechnology 17: 4873.
55. Mie G (1908) Beiträge zur Optik trüber Medien, speziell kolloidaler Metallösungen. Ann. Phys. 25: 377.
56. Gans R (1915) Über die Form ultramikroskopischer Silberteilchen. Ann. Phys. 352: 270.
57. Maxwell-Garnett JC (1904) Colours in metal glasses and in metallic films. Phil. Trans. R. Soc. Lond. 203: 385.
58. Maxwell-Garnett JC (1906) Colours in metal glasses, in metallic films, and in metallic solutions. II. Phil. Trans. R. Soc. Lond. 203: 385.
59. Elser J, Wangberg R, Podolskiy VA, and Narimanov EE (2006) Nanowire metamaterials with extreme optical anisotropy. Appl. Phys. Lett. 89: 261102.
60. Yeh P, Yariv A, and Hong C-S (1977) Electromagnetic propagation in periodic stratified media. I. General theory. J. Opt. Soc. Am. 67: 423.
61. Tumkur T, Zhu G, Black P, Barnakov YA, Bonner CE, and Noginov MA (2011) Control of spontaneous emission in a volume of functionalized hyperbolic metamaterial. Appl. Phys. Lett. 99: 151115.
62. Krishnamoorthy HNS, Jacob Z, Narimanov E, Kretzschmar I, and Menon VM (2012) Topological transitions in metamaterials. Science 336: 205.
63. Yao J, Liu Z, Liu Y, Wang Y, Sun C, Bartal G, Stacy AM, and Zhang X (2008) Optical negative refraction in bulk metamaterials of nanowires. Science 321: 930.
64. Agranovich VM, Ginzburg VL (1984) Crystal Optics with Spatial Dispersion and Excitons. Springer-Verlag Berlin.
65. Hopfield JJ and Thomas DG (1963) Theoretical and experimental effects of spatial dispersion on the optical properties of crystals. Phys. Rev. 132: 563.
66. Gibbs HM (1985) Optical Bistability: Controlling Light with Light. New York: Academic.
67. Kauranen M, Zayats AV (2012) Nonlinear plasmonics. Nat. Phot. 6: 737.
68. Boyd RW (2003) Nonlinear Optics. New York: Academic.
69. Fatti ND, Bouffanais R, Vallée F, and Flytzanis C (1998) Nonequilibrium electron interactions in metal films. Phys. Rev. Lett. 81: 922.
70. Sun CK, Vallée F, Acioli L, Ippen EP and Fujimoto JG (1993) Femtosecond investigation of electron thermalization in gold. Phys. Rev. B 48: 12365.
71. Wurtz GA, Pollard R, and Zayats AV (2006) Optical bistability in nonlinear surface-plasmon polaritonic crystals. Phys. Rev. Lett. 97: 057402.
72. Smolyaninov II, Davis CC, and Zayats AV (2002) Light-controlled photon tunneling. Appl. Phys. Lett. 81: 3314.
73. Milman P, Keller A, Charron E, and Atabek O (2007) Bell-Type inequalities for cold heteronuclear molecules. Physical Review Letters 99: 130405.
74. Sipe JE, So VCY, Fukui M, and Stegeman GI (1980) Analysis of second-harmonic generation at metal surfaces. Phys. Rev. B 21: 4389.
75. Bigot J-Y, Halte V, Merle J-C, and Daunois A (2000) Electron dynamics in metallic nanoparticles. Chem. Phys. 251: 181.
76. Shahbazyan TV, Perakis IE, and Bigot J-Y (1998) Size-dependent surface plasmon dynamics in metal nanoparticles. Phys. Rev. Lett. 81: 3120.
77. Inouye H, Tanaka K, Tanahashi I, and Hirao K (1998) Ultrafast dynamics of nonequilibrium electrons in a gold nanoparticle system. Phys. Rev. B 57: 11334.
78. Del Fatti N, Voisin C, Achermann M, Tzortzakis S, Christofilos D, and Vallee F (2000) Nonequilibrium electron dynamics in noble metals. Phys. Rev. B 61: 16956.
79. Rotenberg N, Betz M, and van Driel HM (2008) Ultrafast control of grating-assisted light coupling to surface plasmons. Opt. Lett. 33: 2137.
80. MacDonald KF, Samson ZL, Stockman MI, and Zheludev NI (2009) Ultrafast active plasmonics. Nat. Photonics 3: 55.
81. Link S, Burda C, Mohamed MB, Nikoobakht B, and El-Sayed MA (2000) Femtosecond transient-absorption dynamics of colloidal gold nanorods: shape independence of the electron-phonon relaxation time. Phys. Rev. B 61: 6086.
82. Wiederrecht GP, Wurtz GA, and Bouhelier A (2008) Ultrafast hybrid plasmonics. Chem. Phys. Lett. 461: 171.
83. Varnavski OP, III TG, Mohamed MB, and El-Sayed MA (2005) Femtosecond excitation dynamics in gold nanospheres and nanorods. Phys. Rev. B 72: 235405.
84. Sönnichsen C, Franzl T, Wilk T, Plessen Gv, Feldmann J, Wilson O, and Mulvaney P (2002) Drastic reduction of plasmon damping in gold nanorods. Phys. Rev. Lett. 88: 077402.
85. Ozcelik S, Ozcelik I, and Akins DL (1998) Superradiant lasing from J-aggregated molecules adsorbed onto colloidal silver. Appl. Phys. Lett. 73: 1949.
86. Wiederrecht GP, Wurtz GA, and Hranisavljevic J (2004) Coherent coupling of molecular excitons to electronic polarizations of noble metal nanoparticles. Nano Lett. 4: 2121.
87. Bellessa J, Bonnand C, Plenet JC, and Mugnier J (2004) Strong coupling between surface plasmons and excitons in an organic semiconductor. Phys. Rev. Lett. 93: 036404.
88. Dintinger J, Klein S, Bustos F, Barnes WL, and Ebbesen TW (2005) Strong coupling between surface plasmon-polaritons and organic molecules in subwavelength hole arrays. Phys. Rev. B 71: 035424.
89. Lidzey DG, Bradley DDC, Armitage A, Walker S, and Skolnick MS (2000) Photon-mediated hybridization of Frenkel excitons in organic semiconductor microcavities. Science 288: 1620.
90. Hobson PA, Barnes WL, Lidzey DG, Gehring GA, Whittaker DM, Skolnick MS, and Walker S (2002) Strong exciton–photon coupling in a low-Q all-metal mirror microcavity. Appl. Phys. Lett. 81: 3519.
91. Christ A, Tikhodeev SG, Gippius NA, Kuhl J, and Giessen H (2003) Waveguide-plasmon polaritons: strong coupling of photonic and electronic resonances in a metallic photonic crystal slab. Phys. Rev. Lett. 91: 183901.
92. Bohren CF, Huffmann DR (1983) Absorption and Scattering of Light by Small Particles. New York: Wiley Science.
93. Ambjörnsson T, Mukhopadhyay G, Apell SP, and Käll M (2006) Resonant coupling between localized plasmons and anisotropic molecular coatings in ellipsoidal metal nanoparticles. Phys. Rev. B 73: 085412.
94. Agranovich VM, Litinskaia M, and Lidzey DG (2003) Cavity polaritons in microcavities containing disordered organic semiconductors. Phys. Rev. B 67: 085311.
95. Dickson W, Wurtz GA, Evans PR, Pollard RJ, and Zayats AV (2008) Electronically controlled surface plasmon dispersion and optical transmission through metallic hole arrays using liquid crystal. Nano Lett. 8: 281.
96. Chu KC, Chao CY, Chen YF, Wu YC, and Chen CC (2006) Electrically controlled surface plasmon resonance frequency of gold nanorods. Appl. Phys. Lett. 89: 103107.
97. Müller J, Sönnichsen C, Poschinger Hv, Plessen Gv, Klar TA, and Feldmann J (2002) Electrically controlled light scattering with single metal nanoparticles. Appl. Phys. Lett. 81: 171.
98. Kossyrev PA, Yin A, Cloutier SG, Cardimona DA, Huang D, Alsing PM, and Xu JM (2005) Electric field tuning of plasmonic response of nanodot array in liquid crystal matrix. Nano Lett. 5: 1978.
99. Yakovlev VV, Dickson W, McPhillips J, Pollard RM, Podolskiy VA, Zayats AV (2013) Ultrasensitive nonresonant detection of ultrasound with plasmonic metamaterials. Adv. Mat. DOI: 10.1002/adma.201300314
100. Veniaminova Y, Stashkevich AA, Roussigne Y, Cherif SM, Murzina TV, Murphy AP, Atkinson R, Pollard RJ, and Zayats AV (2012) Brillouin light scattering by spin waves in magnetic metamaterials based on Co nanorods. Opt. Mater. Express 2: 1260.
101. Hendren WR, Murphy A, Evans P, O'Connor D, Wurtz GA, Zayats AV, Atkinson R, and Pollard RJ (2008) Fabrication and optical properties of gold nanotube arrays. J. Phys. Condens. Matter 20: 362203.
102. Murphy A, Mcphillips J, Hendren W, Mcclatchey C, Atkinson R, Wurtz G, Zayats AV, and Pollard RJ (2011) The controlled fabrication and geometry tuneable optics of gold nanotube arrays. Nanotechnology 22: 045705.