5
Loss Compensation and Amplification of Surface Plasmon Polaritons
5.1 INTRODUCTION
Surface plasmon polaritons (SPPs) exhibit interesting and useful properties such as energy asymptote in dispersion curves, resonant modes, field localization and enhancement, high sensitivities (surface and bulk), and subwavelength confinement [1]. Because of these attributes, SPPs have found uses in several areas including nanophotonics [2, 3], biosensing [4], and integrated optical circuits [5].
Attenuation, however, limits the SPP propagation length, which in turn limits the scope for applications. SPPs dissipate their energy mostly by interacting with the metal. For a metal bounded by an ideal dielectric, loss is caused by free-electron scattering and absorption via interband transitions at short enough wavelengths. These loss mechanisms are fundamental: The latter may be avoided by selecting a long operating wavelength, but the former cannot be eliminated although its effects can be reduced via improved fabrication. Roughness along the metal interface causes additional loss by scattering SPPs into bulk waves.
Loss compensation and amplification can be achieved by adding optical gain to the dielectric(s) bounding the metal [6]. Loss compensation means that the SPP attenuation is reduced compared to the passive case whereas amplification means that it is overcompensated. The amplification of SPPs potentially leads to several interesting, useful, and compelling applications, motivating much of the research on this topic. SPP amplifiers are envisaged as stand-alone components, or “gain blocks” integrated with plasmonic elements, biosensors, or integrated circuits to compensate losses and improve performance. Combining feedback with amplification leads to SPP oscillation, which is of interest as an SPP source. Such applications can be achieved with nanoscale structures because SPPs can be confined to deep subwavelength dimensions. This chapter reviews work conducted on SPP loss compensation and amplification in SPP waveguides; the chapter is organized in terms of SPP waveguide types.
5.2 SURFACE PLASMON WAVEGUIDES
An SPP is a transverse magnetic (TM)-polarized optical surface wave that propagates along a metallo-dielectric structure, typically at visible or infrared wavelengths [1]. It is a coupled excitation, which comprised a charge density wave in the metal and electromagnetic fields that peak at metal–dielectric interfaces and decay exponentially away.
5.2.1 Unidimensional Structures
The simplest SPP waveguide is the single metal–dielectric interface sketched in Figure 5.1a. The wavenumber of the single-interface SPP is given by [1] α + jβ = j(2π/λ0)[
r, mr, d/(r, m + r, d)]1/2, where r, m and r, d are the relative permittivity of the metal and dielectric, respectively, and λ0 is the free-space wavelength (e+jωt time-harmonic form implied; the SPP fields evolve as e−(α+jβ)z for propagation in the +z-direction).
FIGURE 5.1 (a–c) 1D and (d–f) 2D SPP waveguides. (a) Metal (dark gray)–dielectric (light gray) interface with the SPP mode fields (Re{Ey}—left, Re{Hx}—right) transverse to the direction of propagation (z). (b) Symmetric metal film and (c) symmetric metal clads; Re{Ey} of the symmetric (left) and asymmetric (right) SPP supermodes also shown. (d) Dielectric-loaded (dark gray), (e) metal stripe, and (f) gap waveguides; the distribution of the transverse electric field magnitude of the main symmetric SPP mode is also shown. (Adapted from Reference 6.)
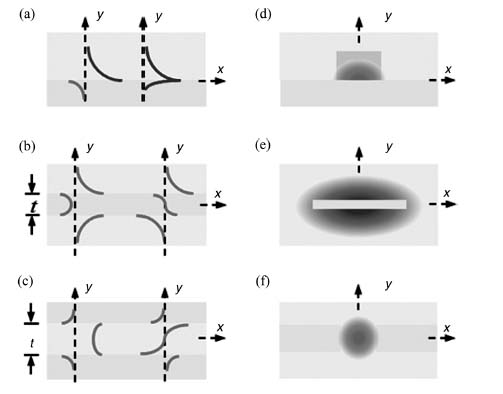
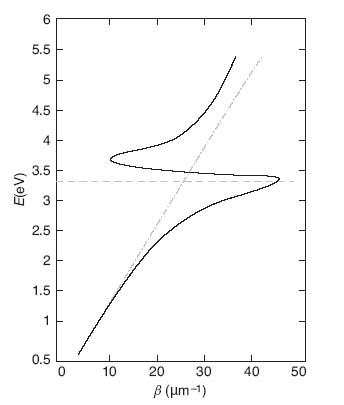
Metals have Re{r, m} < 0 and are dispersive, which causes the SPP wavenumber to diverge at a specific wavelength—the photon energy corresponding to this wavelength is termed the energy asymptote. Table 5.1 gives the modal characteristics of the SPP on an Ag–SiO2 interface at three wavelengths, including near the asymptote (λ0 = 360 nm) [7]; neff = βλ0/2π, δw is the 1/e mode field width, and L = 1/(2α) is the 1/e propagation length. As noted, the properties of the SPP reach extrema at the asymptote. However, losses limit its depth (and the extrema) by bending back the dispersion curve to the left of the light line where the SPP becomes radiative, as shown in Figure 5.2.
Table 5.1 Characteristics of the SPP on an Ag–SiO2 Interface [7]
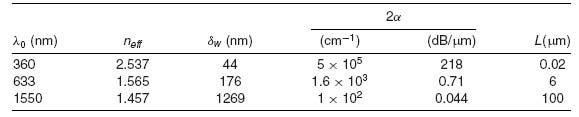
FIGURE 5.2 Dispersion of the single-interface SPP on an Ag–SiO2 interface (E = 
ω vs. β); the dashed-dot curve is the light line in SiO2 and the dashed line marks the energy asymptote. (Adapted from Reference 7.)
The thin metal film bounded by symmetric dielectrics, shown in Figure 5.1b, supports two SPP supermodes created from symmetric or asymmetric couplings of single-interface SPPs [8]. The attenuation of the symmetric mode decreases as the thickness of the metal film decreases (t → 0), to several orders of magnitude lower than the attenuation of the single-interface SPP; the symmetric mode is therefore termed a long-range SPP (LRSPP). The reduced attenuation of the LRSPP, however, comes with reduced confinement [7]. The asymmetric mode behaves oppositely as t decreases and is termed the short-range SPP (SRSPP) [8]. Neither mode has a cutoff thickness. In the Ag–SiO2 system, the power attenuation (2α) of the LRSPP and SRSPP is 2.8 and 1 × 103 cm−1 (0.0012 and 0.45 dB/μm), respectively, for t = 20 nm at λ0 = 1550 nm, increasing as λ0 decreases [7].
Figure 5.1c shows the complementary structure, a thin dielectric film bounded by metal claddings, which also supports SPPs [7]. If the dielectric is thick then several TE and TM parallel-plate-like modes are supported. As the thickness of the dielectric decreases (t → 0) only the symmetric SPP is supported. This mode has no cutoff thickness, so it can be confined to an arbitrarily small width. However, as it shrinks, its attenuation increases, so it is an SRSPP. In the Ag–SiO2 system, its attenuation is 2 × 103 cm−1 (0.85 dB/μm) for t = 50 nm at λ0 = 1550 nm, increasing as λ0 decreases [7].
5.2.2 Bidimensional Structures
Metallo-dielectric structures providing 2D SPP confinement (in the plane transverse to the direction of propagation) also exist; such structures are used to enable integrated optical circuits [5]. Many 2D structures are a natural extension of a 1D counterpart. The dielectric-loaded single interface sketched in Figure 5.1d adds confinement by integrating a high-index region [9]. The SPP is confined therein, and its attenuation ranges from that of the corresponding single-interface SPP to ∼10× higher. The metal stripe sketched in Figure 5.1e produces lateral confinement by limiting the width of the metal film [10]. The attenuation of the LRSPP thereon is ∼10× lower than on the infinitely wide film, but it remains loosely confined. The gap waveguide sketched in Figure 5.1f resembles rotated metal clads [11]. The SPP is strongly confined within the gap and has an attenuation that is comparable in magnitude to the corresponding metal clads.
5.2.3 Confinement-Attenuation Trade-Off
SPP waveguides trade off attenuation for confinement [7]. Whether it appears by varying the wavelength (Table 5.1) or the geometry (Fig. 5.1), the trade-off is fundamental: Increased SPP confinement leads to greater overlap with the metal(s), leading to greater attenuation. SPP attenuation therefore spans, in general, a very broad range (1–105 cm−1), with the most strongly confined modes requiring the greatest gains for loss compensation.
5.2.4 Optical Processes Involving SPPs
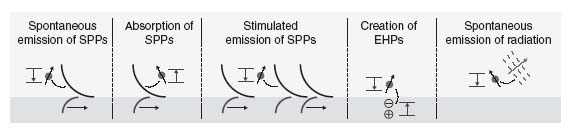
SPPs are bosons, energy quantized in the usual way by analogy with a quantum harmonic oscillator (including material dispersion [12, 13] and absorption [14]). An SPP can gain or lose a quantum of energy in processes involving atoms, molecules, or continuous media, such as spontaneous and stimulated emission, or absorption. Figure 5.3 sketches optical processes that may occur for dipoles near a single metal–dielectric interface. In addition to processes involving SPPs, dipoles may interact with electron–hole pairs in the metal via dipole–dipole transitions if they are close enough or they may emit radiative modes. SPP densities of states can also be defined and used in the assessment of spontaneous emission rates [15].
FIGURE 5.3 Optical processes occurring for dipoles (circles) near a single metal–dielectric interface. The magnitude of the transverse electric field of the SPP involved in the processes is shown along with the associated dipole energy transitions. The dotted curves indicate energy transfer. (Adapted from Reference 6.)
5.3 SINGLE INTERFACE
Prism and grating coupling configurations are commonly used to excite single-interface SPPs [1]. The Kretschmann configuration consists of a metal film on the base of a high-index prism bounded by a lower-index medium on the other side. The grating configuration involves a periodic perturbation in the metal such as corrugations, bumps, or slits. The role of the prism or of the grating is to increase the in-plane momentum of (p-) TM-polarized incident light to match that of the SPP. Several studies involving the single-interface SPP propagating though a gain medium were conducted in such configurations.
5.3.1 Theoretical
The first study of SPP amplification is that of Plotz et al. [16] who considered an Ag film on a prism with the other Ag surface in contact with a gain medium. They computed the reflectance of the glass–metal interface versus the angle of incidence as a function of the material gain, showing that the usual reflectance drop which occurs at the SPP excitation angle [1] becomes monotonically shallower as the gain increases, eventually becoming larger than one, corresponding to amplified total reflection. Sudarkin and Demkovich [17] investigated a similar structure over a broader range of parameters. They found that the reflectance does not always increase monotonically with gain; however, the SPP field increases and the resonance linewidth narrows, both monotonically with gain as expected for SPPs of decreasing attenuation. They suggested the concept of an SPP laser.
The behavior of the SPP near its energy asymptote was investigated on flat and corrugated (∼10 nm period) Ag surfaces in contact with a gain medium [18]. It was found that a material gain of ∼80, 000 cm−1 is required to compensate losses and restore the properties of the SPP near the energy asymptote, spoiled in the passive case by bend-back. A low group velocity (∼1 km/s), a large SPP effective index (∼29), and strong SPP localization (few nanometers) are predicted on gain-compensated gratings. The large material gain required is challenging, but it is interesting to note the potential for extreme performance.
Nezhad et al. [19] investigated SPP amplification along the interface of Ag and an InGaAsP gain medium, predicting lossless propagation at λ0 = 1550 nm for a material gain of ∼1260 cm−1. Kumar et al. [20] also investigated the interaction of SPPs with a semiconductor gain medium (GaAs), modeling the diode structure and carrier injection levels required for amplification.
Lu et al. [21] modeled the optical parametric amplification of SPPs in an Ag–LiNbO3 structure. They find seed and pump wavelengths for which phase matching occurs and then predict gains of ∼30 dB over 3 mm of interaction length for a pump intensity of 50 MW/cm.
5.3.2 Experimental
Oscillation (lasing) involving SPPs was first demonstrated in quantum cascade lasers operating at far-infrared wavelengths [22, 23]. In one device [23] a bimetallic (Ti/Au) grating was used to form a distributed-feedback SPP laser emitting at λ0 ∼ 17 μm. This device owes its success to the low loss of metals at long wavelengths.
The first observations of stimulated emission of SPPs at optical wavelengths were reported in Kretschmann structures consisting of 39 and 67 nm thick Ag films on BK7 prisms with the other Ag surface in contact with the gain medium [24]. Rhodamine 101 and cresyl violet in ethanol (concentrations of N = 7×1017 cm−3) were used as gain media. TM-polarized light at λ0 = 633 nm was used to excite probe SPPs at the Ag/dye interface, while the dye was excited at λ0 = 580 nm (∼10 mW) by pump SPPs counter-propagating along the same interface. The differential reflectance, measured as a function of the probe incidence angle with and without pumping, was attributed to stimulated emission of probe SPPs. Increased reflectance was noted over the SPP excitation angle for the 39 nm Ag films, in qualitative agreement with theory [16], whereas a narrowing and deepening of the reflectance dip was noted for the 67 nm Ag films, also in qualitative agreement with theory [17].
A similar structure was investigated by Noginov et al. [25] but with the gain medium formed as a 10 μm thick layer of PMMA highly doped with Rhodamine-6G (R6G, N = 2.2×1022 cm−3). They strongly pumped the structure from the back (∼18 mJ pulses, ∼10 ns duration, λ0 = 532 nm) and excited probe SPPs via the prism at λ0 = 594 nm. They measured an increase in reflectance at the SPP excitation angle during pump pulses due to stimulated emission of SPPs and estimated via modeling an SPP loss reduction of 35% and a material gain of ∼420 cm−1. In other experiments incorporating a thinner gain layer (∼3 μm), they measured the fluorescence decoupled from the prism during pumping in the absence of the probe, observing characteristics of amplified spontaneous emission (ASE) which they attributed to the stimulated emission of SPP [26].
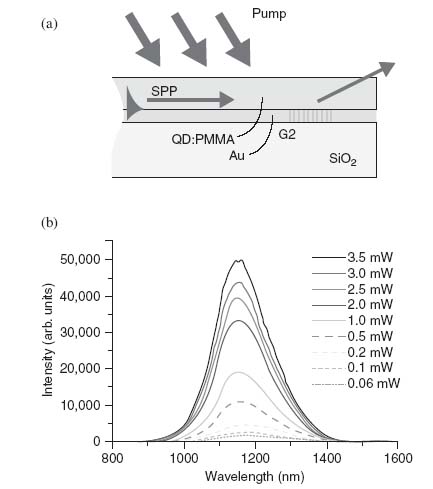
The amplified spontaneous emission of SPPs (ASE-SPP) was also observed by Bolger et al. [27] on a 100 nm thick Au film coated with a ∼1 μm thick film of PMMA doped with PbS quantum dots (QDs). A grating was created in the metal film to out-couple SPPs at wavelengths near the QD emission peak, as shown in Figure 5.4a. Output spectra narrowed as the pump power increased, as shown in Figure 5.4b, indicating ASE-SPP. They estimate a ∼30% increase in SPP propagation length due to stimulated emission and point out that significant gain depletion may occur due to ASE-SPP.
FIGURE 5.4 (a) SPPs propagating through a QD-doped PMMA layer; grating G2 out-couples SPPs into bulk waves. (b) Measured ASE-SPP spectra for increasing pump irradiance. (Adapted from Reference 27.)
5.4 SYMMETRIC METAL FILMS
As discussed in Section 5.2, a thin metal film (Fig. 5.1b) or stripe (Fig. 5.1e) bounded by nearly symmetric dielectrics supports LRSPPs [8]. Less gain is required to amplify LRSPPs compared to single-interface SPPs due to the significantly lower attenuation of the former.
5.4.1 Gratings
It was suggested that a 2D corrugated grating formed from a thin metal film supporting LRSPPs would operate as an SPP bandgap laser if a gain medium having its peak emission within the bandgap was incorporated into the structure [28–30]. An ∼20 nm thick corrugated Ag film, bounded symmetrically by DCM-doped Alq3 as the gain medium, was proposed and it was argued that sufficient gain could be provided to overcome LRSPP losses. In this concept, standing LRSPP waves would be amplified by stimulated emission and partially out-coupled by the grating to form the laser output. Winter et al. [31] also investigated this concept, pointing out that dipole decay into the asymmetric SRSPP (which is also supported by the structure—see Section 5.2) is substantial and will reduce the gain available to the LRSPP.
Kovyakov et al. [32] also studied SPPs on a symmetric grating bounded by a gain layer(s) on one or both sides. They computed the reflectance and transmittance under normal incidence for a 90 nm thick bimetallic (Au/Ag) grating, showing that they simultaneously diverge on resonance when the gain precisely compensates the loss of the excited SPP. They predict 20 dB of transmittance and reflectance for a material gain of 4670 cm−1 when the symmetric mode is excited (however, this computation assumes that the system would remain stable, i.e., that oscillation would not occur).
5.4.2 Theoretical
Nezhad et al. [19] modeled the amplification of LRSPPs on a 40 nm thick Ag film and a similar 400 nm wide stripe, bounded by an InGaAsP gain medium, finding that the material gain required for lossless propagation at λ0 = 1550 nm was ∼10× smaller than for the single-interface SPP. Alam et al. [33] also modeled the amplification of LRSPPs, but along a 10 nm thick, 1 μm wide Ag stripe on AlGaInAs multiple quantum wells (MQWs) covered by barrier material, predicting that a material gain of ∼400 cm−1 was required for lossless propagation at λ0 = 1550 nm.
Genov and coworkers [34, 35] introduced a quasi-permittivity for the metal film such that approximate explicit solutions to the IMI's transcendental equation could be derived. They then investigated an Ag film bounded by InGaAsP [34] and InGaN [35] MWQ gain media and computed the gains required for lossless propagation of the symmetric and asymmetric SPPs.
Chen and Guo [36] computed the Q and threshold gain of LRSPP whispering gallery modes in GaAs-based microdisk cavities incorporating a thin metal film, finding high Qs (∼4000) and a low threshold gain (∼200 cm−1) at λ0 = 1400 nm.
De Leon and Berini [37, 38] constructed a theoretical model for SPP amplification, considering a four-level gain medium, an inhomogeneous pump intensity distribution, and a position-dependent dipole lifetime, finding that if both distributions are neglected the material gain required for lossless propagation can be underestimated by ∼10×. They considered R6G in solvent as the gain medium, and predicted lossless LRSPP propagation at λ0 = 560 nm under modest pumping (λ0 = 532 nm, ∼200 kW/cm2) for a modest dye concentration (N = 1.8×1018 cm−3) assuming a 20 nm thick Ag film covered by the gain medium. They also predict lossless propagation of the single-interface SPP in a similar system but under significantly stronger pumping (∼3.5 MW/cm2) and a higher dye concentration (N = 2.4×1019 cm−3).
5.4.3 Experimental
Ambati et al. [39] observed stimulated emission of LRSPPs at λ0 = 1532 nm on a ∼20 nm thick, 8 μm wide Au stripe embedded in Er-doped glass. They used a co-propagating LRSPP pump/probe arrangement.
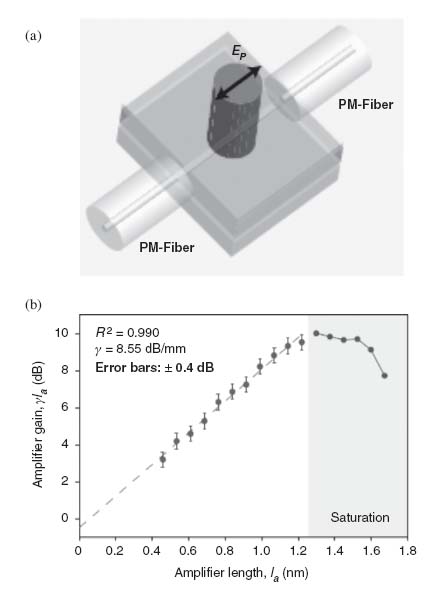
De Leon and Berini [40] reported measurements of LRSPP amplification in an insertion arrangement, as sketched in Figure 5.5a. The structure investigated consisted of an Au stripe (20 nm thick, 1 μm wide, 2.7 mm long) on 15 μm of SiO2 on Si, covered by ∼100 μm of dye solution (IR-140, N = 6×1017 cm−3) index-matched to SiO2. The structure was pumped from the top (λ0 = 808 nm, 20 mJ/cm2, 8 ns pulses) and probed at λ0 = 882 nm via end-fire-aligned polarization-maintaining single-mode optical fibers having a 92% coupling efficiency per facet to the LRSPP. The insertion gain was measured versus amplifier (pump) length la, as shown in Figure 5.5b, from which the slope of the best-fitting linear model yields the LRSPP small-signal mode power gain coefficient, in this case, of γ = 8.55 dB/mm (∼20 cm−1).
FIGURE 5.5 (a) LRSPP amplifier formed as an Au stripe on SiO2 (on Si) covered by a dye gain medium (IR-140). The pump is polarized along the stripe length (Ep) and applied to the top of the structure. End-fire-coupled input/output polarization-maintaining fibers are also shown. (b) Measured amplifier gain at a probe wavelength of λ0 = 882 nm versus amplifier (pump) length la; the slope of the curve gives the LRSPP mode power gain (γ = 8.55 dB/mm). (Adapted from Reference 40.)
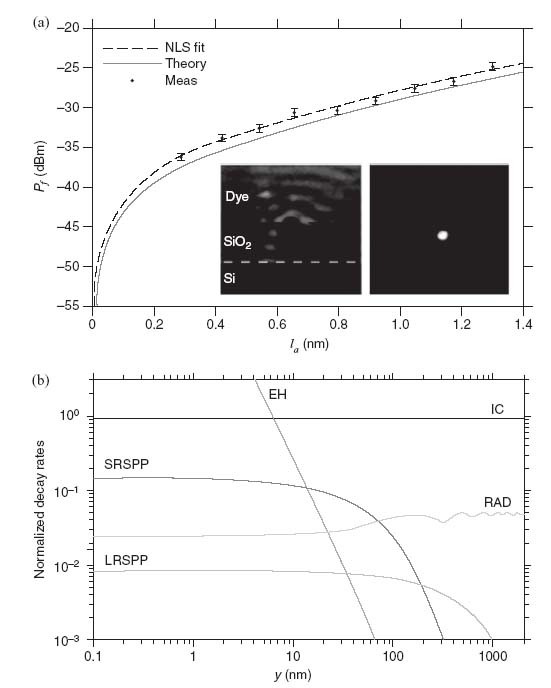
In a subsequent study [41] they measured ASE into the LRSPP, revealing spectrum narrowing with increasing pump length. The output power at the peak ASE-LRSPP wavelength was measured as a function of amplifier length, as shown in Figure 5.6a. The images in the inset of Figure 5.6a show the output of a structure with the pump on but the probe off (left), and the pump off but the probe on (right). An exponential model for the output power was fitted to the measurements (dashed curve), from which an effective input noise power per unit bandwidth of ∼3.3 photons per (LRSPP) mode was deduced along with an LRSPP gain of ∼17 cm−1. They relate this low noise power to the low spontaneous emission rate of dipoles into the LRSPP. The computed normalized dipole (isotropic) decay rates into the various channels supported by a symmetric metal slab (w = ∞) reveal that LRSPPs receive less spontaneous emission compared to other channels, as shown in Figure 5.6b. Using these decay rates, a theoretical model for ASE-LRSPP was constructed and compared to the experimental results (blue curve, Fig. 5.6a), revealing good agreement. Details on their measurement setup and characterization techniques were also reported [42].
FIGURE 5.6 (a) Measured ASE-LRSPP (dots), corresponding to nonlinear least squares (NLS) best-fitting curve (dashed) and theoretical curve (solid). The images in inset show the output of a structure with the pump on but probe off (left) and the pump off but probe on (right). (b) Normalized dipole (isotropic) decay rates into the various channels supported by a symmetric metal slab (w = ∞). (Adapted from Reference 41.)
Gather et al. [43] reported LRSPP gain at visible wavelengths in a symmetric structure comprising a 4 nm thick Au film and a 1 μm thick polymeric gain layer. The structure was pumped from the top (λ0 = 532 nm, 5 ns pulses), and ASE-LRSPP was measured as a function of pump intensity and pump length. They report spectrum narrowing, a threshold behavior in the emitted intensity, and an LRSPP gain coefficient of ∼8 cm−1 at λ0 ∼ 600 nm.
Flynn et al. [44] demonstrated LRSPP lasing at λ0 ∼ 1.46 μm in a symmetric InP-based structure comprised of a 15 nm thick Au film placed between MQW stacks providing TM gain. Each stack was formed from eight tensile InGaAs QWs separated by compressive InAlAs barriers. LRSPP lasing from a 1 mm long, 100 μm wide Fabry–Perot cavity was observed as TM-polarized light emitted from an end facet while pumping from the top (λ0 = 1.06 μm, 140 ns pulses). The emitted power was linearly dependent on the pump intensity (beyond a clear threshold), and the emitted spectrum narrowed with increasing pump intensity.
5.5 METAL CLADS
As discussed in Section 5.2, a thin dielectric or semiconducting film bounded by metal clads (Fig. 5.1c) supports strongly confined symmetric SRSPPs. More gain is required to amplify SRSPPs compared to single-interface SPPs due to the significantly higher attenuation of the former. Nonetheless, studies have shown that semiconductor gain media can provide enough gain to compensate losses in some structures.
5.5.1 Theoretical
Maier [45] determined that material gains of 1625 and 4830 cm−1 are required for lossless (symmetric) SRSPP propagation at λ0 = 1500 nm in structures comprised of, respectively, a 500 and 50 nm thick semiconductor film cladded by Au. Chang and Chuang [46, 47] derived quasi-orthogonality and normalization conditions for SPP modes, then formulated a model for metal-cladded semiconductor amplifiers considering various definitions for the confinement factor (they proposed a definition based on energy and showed that it remains less than unity). Li and Ning [48] find that the mode power gain of the SPP near its energy asymptote is much larger than the material gain, due to low mode energy velocity near the asymptote. Chen et al. [49] applied a model capable of handling temperature-dependent carrier dynamics in semiconductors to an Au–InGaAs–Au structure, predicting lossless SRSPP propagation at λ0 = 1550 nm for a material gain of 2500 cm−1 in a 75 nm thick structure; they also investigated the performance of a nano-ring laser, predicting a threshold lasing current (density) of ∼550 nA (1 kA/cm2).
Yu et al. [50] investigated the transmission and reflection characteristics of a short length of metal-cladded waveguide coupled to a small cavity filled with gain medium (InGaAsP). They showed that the cavity losses can be fully compensated and the performance of the structure fully restored for a material gain of ∼2000 cm−1 (at λ0 ∼ 1550 nm).
5.5.2 Experimental
Hill et al. [51] demonstrated electrically pumped lasing in the symmetric SRSPP in narrow vertical structures formed on rectangular (etched) InGaAs pillars by coating the latter with a 20 nm thick silicon nitride passivation layer, then by a thick Ag layer. Subwavelength confinement occurs along the horizontal dimension, index confinement to the gain region occurs along the vertical dimension, and mirror reflections at the end facets define a Fabry–Perot cavity. Laser emission was detected at a temperature of 10 K as leakage radiation through the substrate.
5.6 OTHER STRUCTURES
5.6.1 Dielectric-Loaded SPP Waveguides
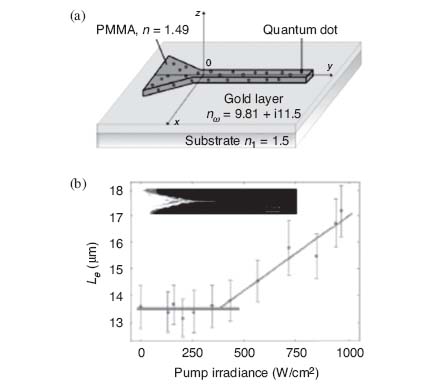
As discussed in Section 5.2 (Fig. 5.1d), a dielectric region having a refractive index higher than that of the surrounding environment (usually air) provides additional confinement by index contrast. Grandidier et al. [52] investigated waveguides comprised of PMMA stripes (∼600 × 400 nm2) doped with PbS QDs defined on a ∼40 nm thick Au film, as sketched in Figure 5.7a. Measurements of spontaneous and stimulated emission into SPPs were obtained via Fourier-plane leakage radiation microscopy (FP-LRM) at λ0 ∼ 1550 nm (near the QD emission peak) while pumping from the top at λ0 = 532 nm. The SPP propagation length was measured as a function of pump intensity while probing at λ0 = 1550 nm, as shown in Figure 5.7b. A distinct threshold is observed beyond which the propagation length increases linearly with the pump; a maximum increase of ∼27% was noted. In a subsequent paper [53] they investigated CdSe/ZnSe QD-doped PMMA stripes on an Ag film, measuring a comparable increase in propagation length at λ0 = 632.8 nm. Radko et al. [54] reported a 32% increase in SPP propagation length in PbS QD-doped PMMA stripes on Au at λ0 ∼ 860 nm. Colas Des Francs et al. [55] modeled structures including gain, reproducing measurements reported earlier [52], while extracting the cross section for stimulated emission of PbS QDs. Rao and Tang [56] modeled structures at wavelengths close to the SPP energy asymptote, finding that nanoscale dielectric cross sections (∼22 × 20 nm2) with ∼5 × 104 cm−1 of gain in the dielectric would provide lossless subwavelength propagation at λ0 = 450 nm.
FIGURE 5.7 (a) Sketch of a dielectric-loaded SPP waveguide comprising a QD-doped PMMA ridge. (b) Measured SPP propagation length (Le) for increasing pump irradiance; the inset shows a near-field scan captured above the waveguide (without pumping). (Adapted from Reference 52.)
5.6.2 Hybrid SPP Waveguide
A metal surface covered by a low-index dielectric then by a high-index dielectric supports a TM-polarized hybrid SPP exhibiting field localization in the low-index dielectric and a high attenuation (compared to LRSPPs) [57, 58]. The high-index dielectric can be a gain medium, leading to loss compensation and lasing in the hybrid SPP, when the latter overlaps sufficiently with the gain medium. Laser-like behavior was observed in such structures, where a CdS nanowire [59] or patch [60] was used as the gain medium.
5.6.3 Nanostructures
Small metal particles support resonant surface plasmon modes. The latter depend on particle shape, size, and composition and the surrounding dielectric [61, 62]. The fundamental resonant mode of, for example, a spherical metal nanoparticle is dipolar, with densities of opposite charge forming at opposite spherical caps. The behavior of resonant modes on metal nanoparticles coupled to a gain medium is of interest because such a system may lead to spasers [63–65] or exhibit near-singular scattering properties [66–68]. (A detailed review of such structures extends beyond the scope of our chapter—the reader is referred to Reference 6 for a discussion.)
5.7 CONCLUSIONS
Metallo-dielectric structures guide SPPs but they do so with the drawback of high attenuation. Incorporating optical gain for loss compensation allows SPPs to propagate longer distances and alters the confinement–attenuation trade-off.
The approximate small-signal material gains required for lossless SPP propagation are (in order of increasing confinement) 1–200 cm−1 for LRSPPs along thin (∼20 nm) metal films; 1000–2000 cm−1 for single-interface SPPs; 2000–5000 cm−1 for SPPs along thin (∼50 nm) metal-cladded waveguides; and 80, 000 cm−1 for SPPs near their energy asymptote. Except perhaps for the latter, such gain levels are available from dyes and semiconductor quantum structures. Optical dipoles (e.g., dyes) can be incorporated into dielectrics (polymers, glasses) and integrated with metal structures. Semiconductors (epitaxial) can be pumped electrically; however, they can be difficult to integrate with a target metallic structure and the gain may be polarization-dependent so alignment of the medium with the SPP fields is necessary.
Significant progress on SPP amplification and lasing has been reported, but much work remains, particularly on the development of applications where performance and usability are paramount. Aspects requiring improvements and further work include pumping (electrical is more convenient), resonators (Q worsens as confinement increases), power dissipation (severely limited in several applications), energy efficiency (more is better), signal-to-noise (noise constrains communication), operating temperature (room temperature is more practical), and stability (large material gains can lead to undesired oscillation).
Although challenges remain, the prospects for SPP amplifiers and lasers are bright. Demonstrations of amplification (overcompensation of loss) and lasing (oscillation) have already been reported involving several kinds of SPPs on many metallic structures, including single-interface SPPs [23], LRSPPs on stripes [40] and slabs [43, 44], and SPPs in metal-cladded [51] and hybrid [60] waveguides. Building on such demonstrations should lead to useful applications.
REFERENCES
1. Maier SA (2007) Plasmonics: Fundamentals and Applications. Springer.
2. Barnes WL, Dereux A, Ebbesen TW (2003) Surface plasmon subwavelength optics. Nature 424: 824–830.
3. Gramotnev DK, Bozhevolnyi SI (2010) Plasmonics beyond the diffraction limit. Nat. Photonics 4: 83–91.
4. Homola J (2008) Surface plasmon resonance sensors for detection of chemical and biological species. Chem. Rev. 108: 462–493.
5. Ebbesen TW, Genet C, Bozhevolnyi SI (2008) Surface plasmon circuitry. Phys. Today 61: 44–50.
6. Berini P, De Leon I (2012) Surface plasmon-polariton amplifiers and lasers. Nat. Photonics. doi: 10.1038/nphoton.2011.285.
7. Berini P (2006) Figures of merit for surface plasmon waveguides. Opt. Express 14: 13030–13042.
8. Berini P (2009) Long-range surface plasmon polaritons. Adv. Opt. Photonics 1: 484–588.
9. Hohenau A, et al. (2005) Dielectric optical elements for surface plasmons. Opt. Lett. 30: 892–895.
10. Berini P (2000) Plasmon-polariton waves guided by thin lossy metal films of finite width: bound modes of symmetric structures. Phys. Rev. B 61: 10484–10503.
11. Pile DFP, et al. (2005) Two-dimensionally localized modes of a nanoscale gap plasmon waveguide. Appl. Phys. Lett. 87: 261114.
12. Nkoma J, Loudon R, Tilley DR (1974) Elementary properties of surface plasmons. J. Phys. C 7: 3547–3559.
13. Archambault A, Marquier F, Greffet J-J (2010) Quantum theory of spontaneous and stimulated emission of surface plasmons. Phys. Rev. B 82: 035411.
14. Matloob R, Loudon R, Barnett SM, Jeffers J (1995) Electromagnetic field quantization in absorbing dielectrics. Phys. Rev. A 52: 4823–4838.
15. Barnes WL (1998) Fluorescence near interfaces: the role of photonic mode density. J. Mod. Opt. 45: 661–669.
16. Plotz G, Simon H, Tucciarone J (1979) Enhanced total reflection with surface plasmons. J. Opt. Soc. Am. 69: 419–422.
17. Sudarkin AN, Demkovich PA (1988) Excitation of surface electromagnetic waves on the boundary of a metal with an amplifying medium. Sov. Phys. Tech. Phys. 34: 764–766.
18. Avrutsky I (2004) Surface plasmons at nanoscale relief gratings between a metal and a dielectric medium with optical gain. Phys. Rev. B. 70: 155416.
19. Nezhad MP, Tetz K, Fainman Y (2004) Gain assisted propagation of surface plasmon polaritons on planar metallic waveguides. Opt. Express 12: 4072–4079.
20. Kumar P, Tripathi VK, Liu CS (2008) A surface plasmon laser. J. Appl. Phys 104: 033306.
21. Lu FF, et al. (2011) Surface plasmon polariton enhanced by optical parametric amplification in nonlinear hybrid waveguide. Opt. Express 19: 2858–2865.
22. Sirtori C, et al. (1998) Long-wavelength (λ ≈ 11.5μm) semiconductor lasers with waveguides based on surface plasmons. Opt. Lett. 23: 1366–1368.
23. Tredicucci A, et al. (2000) Single-mode surface-plasmon laser. Appl. Phys. Lett. 76: 2164–2166.
24. Seidel J, Grafstrom S, Eng L (2005) Stimulated emission of surface plasmons at the interface between a silver film and an optically pumped dye solution. Phys. Rev. Lett. 94: 177401.
25. Noginov MA, et al. (2008) Compensation of loss in propagating surface plasmon polariton by gain in adjacent dielectric medium. Opt. Express 16: 1385–1392.
26. Noginov MA, et al. (2008) Stimulated emission of surface plasmon polaritons. Phys. Rev. Lett. 101: 226806.
27. Bolger PM, et al. (2010) Amplified spontaneous emission of surface plasmon polaritons and limitations on the increase of their propagation length. Opt. Lett. 35: 1197–1199.
28. Okamoto T, H'Dhili F, Kawata S (2004) Towards plasmonic band gap laser. Appl. Phys. Lett. 85: 3968.
29. Okamoto T, Simonen J, Kawata S (2008) Plasmonic band gaps of structured metallic thin films evaluated for a surface plasmon laser using the coupled-wave approach. Phys. Rev. B 77: 115425.
30. H'Dhili F, Okamoto T, Simonen J, Kawata S (2011) Improving the emission efficiency of periodic plasmonic structures for lasing applications. Opt. Commun. 284: 561–566.
31. Winter G, Wedge S, Barnes WL (2006) Can lasing at visible wavelength be achieved using the low-loss long-range surface plasmon-polariton mode? New J. Phys. 8: 125.
32. Kovyakov A, Zakharian AR, Gundu KM, Darmanyan SA (2009) Giant optical resonances due to gain-assisted Bloch surface plasmon. Appl. Phys. Lett. 94: 151111.
33. Alam MZ, Meier J, Aitchison JS, Mojahedi M (2007) Gain assisted surface plasmon polariton in quantum well structures. Opt. Express 15: 176–182.
34. Genov DA, Ambati M, Zhang X (2007) Surface plasmon amplification in planar metal films. IEEE J. Quant. Electron. 43: 1104–1108.
35. Ambati M, Genov DA, Oulton RF, Zhang X (2008) Active plasmonics: surface plasmon interaction with optical emitters. IEEE J. Sel. Top. Quant. Electron. 14: 1395–1403.
36. Chen Y-H, Guo LJ (2011) High Q long-range surface plasmon polariton modes in sub-wavelength metallic microdisk cavity. Plasmonics 6: 183–188.
37. De Leon I, Berini P (2008) Theory of surface plasmon-polariton amplification in planar structures incorporating dipolar gain media. Phys. Rev. B 78: 161401(R).
38. De Leon I, Berini P (2009) Modeling surface plasmon-polariton gain in planar metallic structures. Opt. Express 17: 20191–20202.
39. Ambati M, et al. (2008) Observation of stimulated emission of surface plasmon polaritons. Nano Lett. 8: 3998–4001.
40. De Leon I, Berini P (2010) Amplification of long-range surface plasmons by a dipolar gain medium. Nat. Photonics 4: 382–387.
41. De Leon I, Berini P (2011) Spontaneous emission in long-range surface plasmon-polariton amplifiers. Phys. Rev. B 83: 081414(R).
42. De Leon I, Berini P (2011) Measuring gain and noise in active long-range surface plasmon-polariton waveguides. Rev. Sci. Instrum. 82: 033107.
43. Gather MC, Meerholz K, Danz N, Leosson K (2010) Net optical gain in a plasmonic waveguide embedded in a fluorescent polymer. Nat. Photonics 4: 457–461.
44. Flynn RA, et al. (2011) A room-temperature semiconductor spaser operating near 1.5 m. Opt. Express 19: 8954–8961.
45. Maier SA (2006) Gain-assisted propagation of electromagnetic energy in sub-wavelength surface plasmon polariton gap waveguides. Opt. Commun. 258: 295–299.
46. Chang S-W, Chuang SL (2009) Normal modes for plasmonic nanolasers with dispersive and inhomogeneous media. Opt. Lett. 34: 91–93.
47. Chang S-W, Chuang SL (2009) Fundamental formulation for plasmonic nanolasers. IEEE J. Quant. Electron. 45: 1014–1023.
48. Li DB, Ning CZ (2009) Giant modal gain, amplified surface plasmon-polariton propagation, and slowing down of energy velocity in a metal-semiconductor-metal structure. Phys. Rev. B 80: 153304.
49. Chen X, Bhola B, Huang Y, Ho ST (2010) Multi-level multi-thermal-electron FDTD simulation of plasmonic interaction with semiconducting gain media: applications to plasmonic amplifiers and nano-lasers. Opt. Express 18: 17220–17238.
50. Yu Z, Veronis G, Fan S, Bongersma ML (2008) Gain-induced switching in metal-dielectric-metal plasmonic waveguides. Appl. Phys. Lett. 92: 041117.
51. Hill MT, et al. (2009) Lasing in metal-insulator-metal sub-wavelength plasmonic waveguides. Opt. Express 17: 11107–11112.
52. Grandidier J, et al. (2009) Gain-assisted propagation in a plasmonic waveguide at telecom wavelength. Nano Lett. 9: 2935–2939.
53. Grandidier J, et al. (2010) Leakage radiation microscopy of surface plasmon coupled emission: investigation of gain-assisted propagation in an integrated plasmonic waveguide. J. Microsc. 239: 167–172.
54. Radko IP, Nielsen MG, Albrektsen O, Bozhevolnyi SI (2010) Stimulated emission of surface plasmon polaritons by lead-sulfide quantum dots at near infra-red wavelengths. Opt. Express 18: 18633–18641.
55. Colas Des Francs G, et al. (2010) Optical gain, spontaneous and stimulated emission of surface plasmon polaritons in confined plasmonic waveguide. Opt. Express 18: 16327–16334.
56. Rao R, Tang T (2011) Study on active surface plasmon waveguides and design of a nanoscale lossless surface plasmon waveguide. J. Opt. Soc. Am. B 28: 1258–1265.
57. Alam MZ, Meier J, Aitchison JS, Mojahedi M (2007) Super mode propagation in low index medium. Proc. CLEO, paper JThD112.
58. Oulton RF, Sorger VJ, Genov DA, Pile DFP, Zhang X (2008) A hybrid plasmonic waveguide for subwavelength confinement and long-range propagation. Nat. Photonics 2: 496–500.
59. Oulton RF, et al. (2009) Plasmon lasers at deep subwavelength scale. Nature 461: 629–632.
60. Ma R-M, Oulton RF, Sorger VJ, Bartal G, Zhang X (2011) Room-temperature sub-diffraction-limited plasmon laser by total internal reflection. Nat. Mater. 10: 110–113.
61. Kelly KL, Coronado E, Zhao LL, Schatz GC (2003) The optical properties of metal nanoparticles: the influence of size, shape, and dielectric environment. J. Phys. Chem. B 107: 668–677.
62. Pelton M, Aizpurua J, Bryant G (2008) Metal-nanoparticle plasmonics. Laser Photonics Rev. 2: 136–159.
63. Bergman DJ, Stockman MI (2003) Surface plasmon amplification by stimulated emission of radiation: quantum generation of coherent surface plasmons in nanosystems. Phys. Rev. Lett. 90: 027402.
64. Stockman MI (2008) Spasers explained. Nat. Photonics 2: 327–329.
65. Noginov MA, et al. (2009) Demonstration of a spaser-based nanolaser. Nature 460: 1110–1113.
66. Lawandy NM (2004) Localized surface plasmon singularities in amplifying media. Appl. Phys. Lett. 85: 5040–5042.
67. Gordon JA, Ziolkowski RW (2007) The design and simulated performance of a coated nano-particle laser. Opt. Express 15: 2622–2653.
68. Li Z-Y, Xia Y (2010) Metal nanoparticles with gain toward single-molecule detection by surface-enhanced Raman scattering. Nano Lett. 10: 243–249.