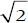) eine irrationale Zahl ist. Brouwer verwarf das »tertium non datur« (ein Drittes gibt es nicht), sobald Unendliches ins Spiel kommt. Für ihn war ein Drittes in Form einer Art Unentschieden möglich.Im vergangenen Jahrhundert explodierte die Mathematik förmlich. Rasante Fortschritte waren in allen ihren Gebieten zu verzeichnen. Es entwickelte sich ein hochgradiges Spezialistentum. Am Ende des Jahrhunderts erschienen weltweit mehr als 2000 mathematische Fachzeitschriften. Kein einzelner Wissenschaftler konnte es mehr schaffen, den Überblick zu behalten.
Dem Laien die Inhalte der neuen Erkenntnisse dieser Epoche nahezubringen, gelingt nur noch in Ausnahmefällen. Allein um die Aufgabenstellungen zu verstehen, ist meist eine mehrjährige Beschäftigung mit der zugrunde liegenden Theorie notwendig.
Ein wachsender Teil der Forschung begründete sich aus innermathematischen Motiven heraus. Zugleich erreichten die Anwendungen in anderen Wissenschaften und der Technik größere Ausmaße als je zuvor – nicht zuletzt auch durch die Erfindung mathematischer Maschinen, wie Computern und anderen elektronischen Geräten.
Begonnen hat das 20. Jahrhundert mit einer Liste von 23 Problemen, denen sich die Zunft der Mathematiker zu stellen hatte. Nicht alle davon sind bis heute gelöst. Doch bestimmte die Auflistung die Richtungen, in die sich die Forschungen wandten.
Wie die Politik trudelte auch die Mathematik in der ersten Hälfte des Jahrhunderts von Krise zu Krise. Zuerst kam es zum großen Grundsatzstreit, welche Art von Beweisen erlaubt sei. Muss man ein mathematisches Objekt konstruieren können oder genügt es, seine Existenz nachzuweisen, ohne es explizit angeben zu können? Philosophisch ist die Debatte immer noch offen, doch hat sich in der Praxis eine Seite klar durchgesetzt.
Als sich das herausschälte, zogen grundlegende Überlegungen der »Königin der Wissenschaft« anscheinend die logische Basis unter den Füßen weg. Obwohl der damals bewiesene Unvollständigkeitssatz immer noch gilt, haben sich die Mathematiker daran gewöhnt, auf einer weniger soliden Grundlage als ursprünglich gedacht zu arbeiten.
Die nächste Krise hatte Ursachen, die nicht auf mathematische Inhalte zurückzuführen waren. Die Nationalsozialisten verfolgten und vertrieben nach ihrer Machtergreifung die jüdischen Mathematiker. Viele davon emigrierten in die USA und sorgten mit dafür, dass Mitte des Jahrhunderts Europa seine führende Rolle an die Neue Welt abtreten musste.
Gegen Ende des Jahrhunderts veränderte der Computer die Szene. Zum einen kamen Beweise von mathematischen Sätzen auf, die nur mit seiner Hilfe funktionierten. Für Puristen war das ein Skandal. Zum anderen setzten sich nun auch reine Mathematiker vor den Bildschirm und probierten ihre Vermutungen an Beispielen im Rechner aus, bevor sie sich ganz klassisch mit Papier und Bleistift an den Beweis wagten.
Neben den Koryphäen des Fachs wie David Hilbert, Kurt Gödel oder Paul Erdös bauten im 20. Jahrhundert Tausende von Mathematikern das Gebäude ihrer Wissenschaft aus. In akribischer Kleinarbeit ersannen sie Begriffe, bewiesen Sätze und schufen neue Theorien. Wie fruchtbar die neuen Ideen waren, zeigte sich immer wieder, wenn es gelang, eine lange offenstehende Vermutung zu beweisen. So wurden in den letzten Jahren des 20. Jahrhunderts zwei mathematische Nüsse geknackt, an denen sich zuvor jahrhundertelang die schlauesten Köpfe die Zähne ausgebissen hatten: Fermats letzter Satz und die Vermutung von Kepler.
»Unermesslich ist die Fülle von Problemen in der Mathematik, und sobald ein Problem gelöst ist, tauchen an dessen Stelle zahllose neue Probleme auf«, sagte David Hilbert im Jahr 1900 auf einer internationalen Tagung in Paris. Um Orientierung zu geben, stellte der Professor der Universität Göttingen in seinem Vortrag 23 Probleme vor, die seine Kollegen in den nächsten Jahren in Angriff nehmen sollten. Er beendete seine Rede mit den Worten: »Die Mathematik ist die Grundlage alles exakten wissenschaftlichen Erkennens. Damit sie diese hohe Bestimmung vollkommen erfülle, mögen ihr im neuen Jahrhundert geniale Meister erstehen und zahlreiche in edlem Eifer erglühende Jünger!«
Da Hilbert damals neben dem Franzosen Henri Poincaré (1854–1912) der weltweit renommierteste Mathematiker war, beeinflusste seine Rede die Forschung der nächsten Jahrzehnte. Wer eines seiner Probleme knackte, dem war der Ruhm gewiss. Daher stürzten sich die fähigsten Köpfe auf sie.
Das erste Problem, die »Kontinuumshypothese«, drehte sich um Cantors Begriff der Unendlichkeit. Cantor hatte nachgewiesen, dass die reellen Zahlen von größerer Unendlichkeit sind als die natürlichen Zahlen. Hilbert fragte nun, ob es zwischen diesen beiden Unendlichkeiten einen weiteren Grad der Unendlichkeit geben könne. Erst 1963 konnte Paul Cohen (1934–2007) das Problem »lösen«, allerdings wohl nicht im Sinne Hilberts. Der US-amerikanische Mathematiker bewies, dass die Kontinuumshypothese weder beweis- noch widerlegbar ist. Dazu stützte er sich auf Arbeiten des aus Österreich stammenden Kurt Gödel (1906–1978), der 35 Jahre zuvor eine überraschende Antwort auf Hilberts zweites Problem fand. Dabei ging es darum, die Widerspruchsfreiheit der Arithmetik zu beweisen.
Natürlich ging Hilbert, ebenso wie die meisten seiner Kollegen, davon aus, dass es in dieser Grundlage jeder Mathematik keinen Widerspruch geben könne. Doch forderte er als gründlicher Wissenschaftler einen Beweis dafür.
Gödel nahm sich des Problems an und stellte fest, dass jedes widerspruchsfreie System von Axiomen, also auch die Arithmetik, Sätze enthält, die weder beweis- noch widerlegbar sind. Ein böser Rückschlag für die Mathematiker, die doch so sehr auf die Kraft der reinen Logik setzten. Nun sollte es Aussagen geben, die sich allen Bemühungen für immer entziehen. Vor allem Hilbert muss das Ergebnis hart getroffen haben. »Da ist das Problem, suche die Lösung. Du kannst sie durch reines Denken finden«, lautete sein Glaubensbekenntnis. »Wir müssen wissen, wir werden wissen!«
Gödels Idee erinnert an logische Paradoxa, die bereits die alten Griechen kannten. Sein Kunstgriff war es, eine Aussage zu formulieren, die sich selbst zum Inhalt hat, wie zum Beispiel: »Diese Behauptung hat keinen Beweis«. Schon schnappt die logische Zwickmühle zu. Entweder ist der Satz falsch, dann hat die Behauptung aber einen Beweis und sollte daher richtig sein. Oder er ist richtig, dann hat er aber keinen Beweis. Gödels Abhandlung ist freilich erheblich mathematischer und komplizierter. Die Grundidee ist indes dieselbe.
Als Österreich 1934 dem deutschen Reich angeschlossen wurde, verlor Gödel seine Dozentenstelle. Als er dann noch als Jude auf der Straße angepöbelt wurde, beschloss er, seine Heimat zu verlassen. 1940 floh er über die Sowjetunion und Japan in die USA. Dort nahm er einen Ruf an die Universität in Princeton an, an der auch Einstein wirkte.
Gödel zeigte sich enttäuscht, dass seine umwerfenden Resultate kein ähnliches Echo hervorriefen wie die wenige Jahre zuvor entdeckte Relativitätstheorie. Doch wollten sich die Mathematiker nicht gerne mit den Grenzen ihrer vergötterten Logik befassen. Zumal die Auswirkungen von Gödels Arbeit beschränkt blieben. Die Mehrheit forschte einfach weiter wie zuvor, ohne sich weiter Gedanken zu machen.
Erst Paul Cohen fand mit der Kontinuumshypothese ein berühmtes Beispiel für den Unvollständigkeitssatz. Der junge Mathematiker reiste auch gleich zu Gödel nach Princeton. Der öffnete ihm die Tür, aber nur so weit, um das Manuskript entgegenzunehmen. Erst nachdem er es studiert hatte, empfing er den Kollegen zum Tee. Gödel litt damals bereits an einer Paranoia anderen Menschen gegenüber. So wollte er oft nichts essen, weil er panische Angst davor hatte, vergiftet zu werden. Lediglich der Fürsorge seiner Frau Adele war es zu verdanken, dass er überhaupt etwas zu sich nahm. Als Adele wegen eines Schlaganfalls ein halbes Jahr im Krankenhaus verbringen musste, hungerte er sich buchstäblich zu Tode.
Hilberts Marotten
David Hilbert muss nicht nur ein hundertprozentiger Mathematiker, sondern auch ein ausgeprägter Charakter gewesen sein. Über ihn kursieren zahlreiche Anekdoten. Ein Beispiel: »Das ist gut so«, soll er einmal über einen seiner Schüler gesagt haben, der Schriftsteller geworden war. »Ich habe nie geglaubt, dass er genug Kreativität für einen Mathematiker mitbringt.«
Eine andere Geschichte ist vermutlich eher gut erfunden als wahr. Hilbert war für sein schwaches Kopfrechnen bekannt. Einmal stand er in seiner Vorlesung vor dem Problem, 8 mal 7 ausrechnen zu müssen: »Nun meine Herren, wie viel ist wohl 8 mal 7?« Ein Student rief: »55?« Daraufhin ein anderer: »57!« Schließlich Hilbert: »Aber meine Herren, die Lösung kann doch nur entweder 55 oder 57 sein!«
Axiome der Arithmetik
Sieben Axiome genügen, um die Arithmetik der ganzen Zahlen zu beschreiben: Für alle Zahlen k, m und n
1. gelten die Kommutativgesetze: k+ m= m+ k und k∙ m= m∙ k.
2. gelten die Assoziativgesetze: (k+ m)+ n= k+(m+ n) und (k∙ m)∙ n= k∙(m∙ n)
3. gilt das Distributivgesetz: k∙(m+ n)= k∙ m+ k∙ n
4. gibt es eine Zahl 0 mit k+0= k
5. gibt es eine Zahl 1 mit k∙1= k
6. gibt es eine Zahl p mit k+ p=0
7. mit k ≠ 0 gilt die Kürzungsregel: aus k∙ m= k∙ n folgt m= n
David Hilbert musste sich nicht nur mit Gödels unerfreulichen Resultaten auseinandersetzen. Er führte auch einen heftigen Streit über die Grundlagen seines Faches. Sein Widersacher dabei war der Niederländer Luitzen Egbertus Jan Brouwer (1881–1966), der einen alternativen Zugang zum Unendlichen vorschlug: die konstruktive Mathematik. In ihr gibt es nur die Objekte, die konstruiert werden können. Reine Existenzbeweise lehnte Brouwer ab. In gewissem Sinn war der Holländer der Erbe von Kronecker. Er ging von den natürlichen Zahlen aus und sah nur das als erlaubt an, was sich aus ihnen in endlich vielen Schritten konstruieren ließ. So wollte er die Paradoxien verhindern, die in Cantors Mengenlehre aufgetreten waren.
Die klassische Mathematik baut schon seit der Antike auch auf indirekten Schlüssen auf, die nach dem Prinzip des ausgeschlossenen Dritten gezogen werden. Beispiele hierfür sind die Beweise, dass es unendlich viele Primzahlen gibt und dass die Wurzel aus 2 (in Zeichen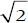) eine irrationale Zahl ist. Brouwer verwarf das »tertium non datur« (ein Drittes gibt es nicht), sobald Unendliches ins Spiel kommt. Für ihn war ein Drittes in Form einer Art Unentschieden möglich.
In der klassischen Mathematik ist eine Zahl entweder Null oder von Null verschieden. Brouwer sah das anders und konstruierte eine Zahl, von der niemand sagen kann, ob sie Null ist oder nicht. Diese sogenannte Brouwersche Zahl ist auf alle Fälle furchtbar klein. Um festzustellen, ob sie tatsächlich exakt mit Null übereinstimmt, müsste man unendlich viele Ziffern betrachten. Und das ist für uns endliche Wesen ein Ding der Unmöglichkeit. Mathematikern mag es als Skandal vorkommen, nicht entscheiden zu können, ob eine Zahl gleich Null ist oder nicht. Programmierer kennen das längst. Da Computer nur mit endlicher Genauigkeit rechnen, steht bei ihnen die Null auch für hinreichend kleine Zahlen.
Zur Definition seiner Zahl zog Brouwer die Nachkommastellen der Kreiszahl Pi (in Zeichen π) heran: 1415926535… Da Pi eine irrationale Zahl ist, bricht die Ziffernfolge hinter dem Komma niemals ab und endet auch nicht in sich fortlaufend wiederholenden Ziffern. Aus ihr bastelte der Holländer seine verschwindend kleine Zahl: Vor dem Komma schrieb er eine 0. An der ersten Stelle dahinter sollte eine 7 stehen, wenn die erste Nachkommastelle von Pi gleich 7 wäre, sonst eine 0. An der zweiten Nachkommastelle sollte eine 7 verzeichnet werden, wenn die zweite und die dritte Nachkommastelle von Pi beide 7 lauteten, sonst eine 0. Auf die dritte Nachkommastelle sollte eine 7 kommen, wenn an der vierten, fünften und sechsten Nachkommastelle von Pi jeweils eine 7 stände, sonst eine 0. Es ist klar, wie die Vorschrift weitergeht. Je größer der Abstand einer Ziffer in der Brouwerschen Zahl vom Komma, desto mehr Siebener müssen in Folge auftreten, damit sie von 0 verschieden ist.
Mittlerweile haben Computer Pi auf viele Milliarden Stellen genau berechnet. Eine ausreichend lange Sequenz von Siebenern tauchte kein einziges Mal auf. Die Brouwersche Zahl beginnt daher mit sehr vielen Nullen hinter dem Komma. Doch ob sie wirklich gleich Null ist, wissen wir nicht und werden wir wohl nie wissen können. Denn es gibt unendlich viele Nachkommastellen von Pi; kein Mensch wird sie alle jemals durchsehen können. Deshalb ist es nicht ausgeschlossen, dass ganz weit hinten in der Brouwerschen Zahl doch noch eine 7 erscheint.
Manchem mag die Argumentation als Haarspalterei vorkommen. Doch brüstet sich die Mathematik gerne damit, die exakteste aller Wissenschaften zu sein und Wahrheiten für die Ewigkeit zu produzieren. Da muss sie sich schon genaues Hingucken gefallen lassen.
Brouwer lehnte die Ideen seiner Zeitgenossen kategorisch ab und verteidigte seinen Ansatz kompromisslos. »Er war ein sonderlicher Mensch, völlig in seine Philosophie vernarrt«, urteilte sein Kollege und Landsmann Bartel van der Warden (1903–1996) über ihn. Sein Hauptgegner Hilbert redete von einem Putsch. Brouwers Vorstellungen seien für seine Zunft so, als ob man Astronomen ihre Fernrohre oder Boxern ihre Handschuhe raubte: »Wir laufen Gefahr, einen großen Teil unserer wertvollsten Schätze zu verlieren, wenn wir solchen Reformatoren folgen.«
Hermann Weyl (1885–1955), ein Schüler Hilberts, gestand zwar ein, das Haus der Mathematik sei »zu einem wesentlichen Teil auf Sand gebaut«. Dennoch wollte er sich nicht vollends der Brouwerschen Revolution, wie er es nannte, anschließen. Er fürchtete, mit dessen Methode nicht alle Ergebnisse herleiten zu können, die in der Physik angewandt wurden.
Diese Sorge hat sich mittlerweile als unberechtigt herausgestellt. Im Laufe des Jahrhunderts gelang es Wissenschaftlern, mit konstruktiver Mathematik alles zu beweisen, was Physiker, Ingenieure und Ökonomen brauchen. Die konstruktiven Beweise gestalten sich zwar oft etwas komplizierter, dafür bieten sie aber auch mehr Einsicht. Denn sie liefern eine Lösung und nicht nur den formalen Schluss, dass es eine solche geben muss.
Computer kennen nur Zahlen mit endlich vielen Nachkommastellen. Daher sind sie Konstruktivisten par excellence. Rund um den Globus arbeiten Forschergruppen daran, konstruktive mathematische Beweise automatisch in Computerprogramme umzuwandeln. Anwendungen erwarten sie bei Datenbanken, Chipdesign und führerlosem Bahnverkehr. Der Vorteil dieser Art, Software zu erstellen: Fehlersuche und Wartung, die heute beim Programmieren den Löwenanteil ausmachen, verringern sich enorm. Denn es lässt sich beweisen, dass die Software genau das tut, was sie soll. Bei herkömmlich geschriebenen Programmen ist ein solcher Nachweis prinzipiell nicht möglich.
Was Brouwer nicht schaffte, könnte so die Softwarebranche nebenbei erledigen: die vernachlässigte konstruktive Mathematik aus ihrem Mauerblümchendasein befreien.
Schon Cäsar (100–44 v. Chr.) schickte seinen Feldherrn Nachrichten so, dass die Feinde sie nicht entziffern konnten. Angeblich ersetzte der römische Herrscher jeden Buchstaben eines Textes durch den Buchstaben, der im Alphabet drei Stellen danach kommt. Für ein A schrieb er also ein D, für ein F ein I.
»ZHU NDQQ GDV OHVHQ?« heißt demnach: »WER KANN DAS LESEN?«
Zumindest bei längeren Botschaften lässt sich die Verschlüsselung problemlos knacken. Denn die Buchstaben kommen unterschiedlich oft vor. In einem normalen deutschen Text etwa entfällt knapp ein Fünftel auf den Buchstaben E. Der zweithäufigste Buchstabe ist N. Mit Computerhilfe kann eine längere Nachricht in wenigen Sekunden entschlüsselt werden: Der Buchstabe, der am häufigsten auftaucht, muss für das E stehen, der am zweithäufigsten für das N, und so weiter.
Verschiebt man die Buchstaben beim Cäsar-Code nicht immer um dieselbe Anzahl Buchstaben, sondern jedes Mal um eine andere, ist der Code nicht mehr zu knacken. Verschieben wir etwa den ersten Buchstaben um 3 Buchstaben, den zweiten um 5 und den dritten um 9, schreibt sich »WER« als »ZJA«. Eine so verschlüsselte Nachricht kann nur in Klartext übersetzen, wer weiß, um wie viel jeder Buchstabe verschoben wird. Da ein Buchstabe, der mehrmals im Text auftaucht, immer wieder mit einem anderen verschlüsselt wird, helfen einem unerwünschten Mithörer die Häufigkeiten der Buchstaben nicht weiter, um die Botschaft zu entziffern. Allerdings hat das Verfahren einen entscheidenden Nachteil: Sender und Empfänger benötigen dazu die gleiche Liste von Zahlen, die angeben, um wie viele Buchstaben jeweils verschoben wird. Und diese Liste muss, will man kein Risiko eingehen, genauso lang sein wie der zu verschlüsselnde Text. Im Kalten Krieg zwischen den USA und der Sowjetunion benutzten beide Seiten ähnliche Verfahren. Der sowjetische Geheimdienst setzte angeblich dieselben Zahlenlisten mehrfach ein. Die Amerikaner konnten dadurch einige Nachrichten entschlüsseln und Agenten enttarnen.
Die Deutschen vertrauten im Zweiten Weltkrieg auf eine Verschlüsselungsmaschine namens Enigma (griechisch für Geheimnis), die aussah wie eine alte Schreibmaschine. In ihrem Inneren bestimmten mehrere sich drehende Walzen, wie ein eingegebener Buchstabe kodiert wurde. Die Walzen konnten ausgetauscht und ihre Stellung zueinander verändert werden. So ließ sich die Maschine auf Milliarden verschiedene Arten einstellen. In Großbritannien sollten Experten unter der Führung des Mathematikers Alan Turing (1912–1954) ihre Codes entschlüsseln. Die Briten bauten den Walzenapparat nach und versuchten, die Stellung der Walzen herauszukriegen, indem sie bestimmte Wörter in der Nachricht errieten. So fanden sie etwa heraus, dass Texte, die gegen 18 Uhr gesendet wurden, am Anfang einen Wetterbericht enthielten. Da die Funksprüche nach strengen Regeln gegliedert waren, kam das Wort »Wetter« jeweils an derselben Stelle vor. Nun fütterten die Briten ihren Nachbau der Enigma mit dem Wort »Wetter« und probierten systematisch, bis die Maschine die richtige Kodierung ausspuckte.
Ab 1943 benutzten sie dabei erste Vorläufer der Computer. So gelang es ihnen häufig, die geheimen Meldungen aus Deutschland zu entschlüsseln. Obwohl zuweilen der Verdacht aufkam, der Feind habe die Enigma geknackt, waren die deutschen Heeresführer von der Sicherheit ihrer Codes überzeugt und sahen keinen Grund, sie zu verändern. Manche Historiker glauben, das habe die Niederlage der Deutschen eingeleitet.
In jüngerer Zeit benutzen nicht nur Militärs und Spione Codes. Wer seine E-Mails verschlüsseln oder Bankgeschäfte online erledigen will, greift auf Programme zurück, die Botschaften mit Hilfe einer großen Zahl verschlüsseln. Um den Code lesen zu können, muss man die Zahl in ihre Faktoren zerlegen. Und das ist, wenn die Zahl groß genug ist, so gut wie unmöglich. Computer können zwar selbst Zahlen mit mehreren hundert Stellen in Sekundenbruchteilen miteinander malnehmen. Andersherum aber das Ergebnis in seine Faktoren zu zerlegen überfordert die schnellsten Elektronenrechner, jedenfalls wenn die Zahl so gewählt ist, dass sie hinreichend große Faktoren besitzt, also etwa zwei mehr als hundertstellige Zahlen.
Mit einem Risiko müssen die Anwender allerdings leben: Sollten Mathematiker eines Tages eine Methode entwickeln, mit der sich große Zahlen mit viel weniger Rechenaufwand in Faktoren zerlegen lassen, als das heute möglich ist, könnten plötzlich alle so kodierten Nachrichten von Unbefugten entziffert werden. Da an dieser Aufgabe seit Jahrzehnten ohne Erfolg geforscht wird, rechnet damit aber niemand.
Am Manhattan-Projekt der USA, in dem Wissenschaftler während des Zweiten Weltkriegs die Atombombe entwickelten, waren zahlreiche Mathematiker beteiligt.
Selbst bei endlichen konstruktiven Berechnungen treten zuweilen seltsame Ergebnisse auf, wie sich mit dem Aufkommen der Computer herausstellte.
Vor rund 60 Jahren fütterte Edward Lorenz (1917–2008) seinen Computer mit Wetterdaten. Weil die Maschinen damals noch sehr langsam waren, arbeitete der US-amerikanische Meteorologe mit einer einfachen Formel, die nur dreierlei berücksichtigte: die Temperatur, die Windstärke und den Wärmefluss. Da Lorenz dem Resultat misstraute, stellte er einen Teil der Rechnung noch mal an. Bei diesem zweiten Durchlauf startete er mit gerundeten Zwischenergebnissen. So tippte er etwa 0,506 anstatt 0,506127 ein. Würde nun etwas anderes herauskommen, musste etwas faul sein, dachte sich der Meteorologe. In der Tat hatten die beiden Ergebnisse wenig miteinander gemein. Die berechneten Wetterlagen sahen völlig verschieden aus. Doch es konnte nicht am Computer liegen: Lorenz gab die ursprünglichen Anfangswerte noch mal ein und erhielt exakt die gleichen Zahlenkolonnen wie beim ersten Mal.
Die Auflösung des Rätsels: Der Rechner arbeitete intern mit mehr als drei Stellen hinter dem Komma. Dieser geringe Unterschied, der zum Beispiel einem zusätzlichen Windhauch hätte entsprechen können, hatte sich hochgeschaukelt und in kurzer Zeit die Prognose durcheinandergewirbelt. Damit war der Schmetterlingseffekt geboren, nach dem winzige Veränderungen der Ausgangsdaten riesige Folgen zeigen können. Seitdem haben die Wetterfrösche die perfekte Ausrede, wenn sie wieder mal daneben langen.
Um den Schmetterlingseffekt auszutricksen und verlässlichere Aussagen zu bekommen, rechnen die Meteorologen die Entwicklung der Messdaten mit jeweils leicht veränderten Anfangswerten mehrmals durch. Die Ausreißer in den Rechenergebnissen werden dann gestrichen, aus dem Rest der Mittelwert gebildet. Das liefert aber höchstens dann verlässliche Resultate, wenn die Vorhersage auf die nächsten Tage beschränkt bleibt. Für längere Zeiträume ergeben sich zu viele große Abweichungen.
Die Wetterforscher berechnen ihre Prognosen Schritt für Schritt. Sie geben Messdaten in den Computer ein, der dann daraus eine Entwicklung des Wetters für die jeweiligen Örtlichkeiten ermittelt. Der Vorhersagezeitraum wird dazu in einzelne Abschnitte, zum Beispiel in Perioden von jeweils vier Stunden, unterteilt und die verschiedenen Größen dafür bestimmt. In die Berechnung von Temperatur, Wind und Feuchte nach dem zweiten Zeitabschnitt gehen die Resultate für den ersten Abschnitt ein. Dadurch können sich Abweichungen hochschaukeln. Startet das Programm etwa mit einer Temperatur von 15,1 statt 15,2 Grad, scheint das keinen großen Unterschied zu machen. In der Tat wird die Temperaturdifferenz nach dem ersten Zeitabschnitt klein bleiben. Aber nach dem zehnten oder zwanzigsten kann sie sich zu mehr als 20 Grad aufgeschaukelt haben.
Können kleine Abweichungen der Ausgangswerte zu großen Unterschieden im Resultat führen, sprechen Wissenschaftler von chaotischen Systemen. Beispiele dafür sind neben dem Wetter etwa Turbulenzen in Flüssigkeiten, der Lauf der Kugel beim Flipper, die Verteilung von Erdbeben oder das Doppelpendel (ein Pendel mit einem Gelenk in der Mitte).
Zu chaotischem Verhalten kommt es immer dann, wenn in dieselbe nicht-lineare Gleichung deren Lösungen immer wieder als Ausgangswerte eingesetzt werden. Nicht-linear bedeutet dabei, dass in der Gleichung die Variablen, also das, was eingesetzt wird, nicht nur in der ersten Potenz auftreten. In den Formeln steht dann zum Beispiel ein x2 oder ein x im Exponenten, wie etwa in 1,1x.
Während das Chaos Meteorologen und Erdbebenforschern Kopfzerbrechen bereitet, führte es in der Geometrie zu einem neuen Ansatz. Benoit Mandelbrot (1924–2010) bemängelte, die euklidische Geometrie eigne sich nicht dazu, die Natur zu beschreiben. Der polnisch-französische Mathematiker, der lange in den USA lebte und arbeitete, schreibt in seinem Buch »Die fraktale Geometrie der Natur«: »Warum wird die Geometrie oft als nüchtern und trocken bezeichnet? Nun, einer der Gründe besteht in ihrer Unfähigkeit, solche Formen zu beschreiben, wie etwa eine Wolke, einen Berg, eine Küstenlinie oder einen Baum. Wolken sind keine Kugeln, Berge keine Kegel, Küstenlinien keine Kreise. Die Rinde ist nicht glatt und auch der Blitz bahnt sich seinen Weg nicht gerade.«
Das Wesen der Natur ist für Mandelbrot die Selbstähnlichkeit. Das heißt, dieselben Formen tauchen in verschiedenen Größen immer wieder auf. So erinnert etwa der Baum an einen Ast, der Ast an einen Zweig, der Zweig an die Verstrebungen in einem Blatt. Betrachtet man eine Küstenlinie von einem Satelliten aus, ist sie ähnlich zerklüftet wie von einem Flugzeug oder Ballon, nur in einem anderen Maßstab.
Wie lang ist die Küste Großbritanniens, fragte Mandelbrot einmal im Titel eines Fachartikels. Seine Antwort darauf: Das kommt darauf an, in welchem Maßstab man sie betrachtet. Je näher man hinschaue, umso mehr Vorsprünge und Einbuchtungen tauchten auf. Das reiche bis in den Größenmaßstab eines Atoms hinein. Die Länge der Küste wachse daher ins Unendliche.
In den Figuren der fraktalen Geometrie tauchen ähnliche Strukturen immer wieder in verschiedenen Größenmaßstäben auf.
Mandelbrot begnügte sich nicht damit, Selbstähnlichkeit als ein wichtiges Prinzip der Natur zu erkennen, er bildete sie auch nach. Dazu berechnete er relativ einfache Formeln und gab das Ergebnis der Rechnung als Ausgangsdaten erneut in die Formeln ein. Diesen Vorgang wiederholte er am Computer unzählige Male und stellte das Ergebnis grafisch dar. Das berühmteste Bild ist die Mandelbrot-Menge, auch Apfelmännchen genannt. Zoomt man in sie hinein, entdeckt man immer wieder ähnliche Strukturen.
In den vergangenen Jahren haben Mathematiker mit Mandelbrots sogenannter fraktaler Geometrie phantasievolle Landschaften und ganze Planeten gezaubert, die den Rahmen für Science-Fiction-Filme und Computerspiele liefern.
Im täglichen Leben sind wir ständig von Zahlen umgeben. Sie stehen in Statistiken, Adressen, Rechnungen, Börsencharts, Sportergebnissen. Eigentümlicherweise treten in ihnen die Ziffern nicht mit gleicher Häufigkeit auf, zumindest nicht an der höchsten Stelle. Bei den meisten Datensätzen fangen mehr als sechsmal so viele Zahlen mit 1 an als mit 9. Das hat Frank Benford (1887–1948) 1938 herausgefunden.
Der amerikanische Physiker und Erfinder des Laserpointers, der bei General Electric arbeitete, bestätigte eine Formel aus dem vergangenen Jahrhundert, derzufolge die Wahrscheinlichkeit, dass eine Zahl mit der Ziffer d beginnt,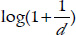 
beträgt.
Mit einem Taschenrechner lassen sich die Chancen für die führenden Ziffern ausrechnen: Zu rund 30 Prozent steht die 1 an erster Stelle, zu knapp 18 Prozent die 2, zu 12 Prozent die 3 und zu 4,5 Prozent die 9.
Wer die seltsam anmutende Regel nicht glauben mag, kann sie selbst testen. Rund ein Drittel der Zahlen in diesem Buch sollten mit 1 beginnen, ein Fünftel mit 2, ein Achtel mit 3 und mit 9 nur noch ein Zwanzigstel. Skeptiker können auch den Google-Test machen. Zu beispielsweise fünfstelligen Zahlen, die mit 1 beginnen, findet die Suchmaschine ungleich mehr Adressen als zu solchen mit einer 5 oder gar einer 9 an führender Stelle.
In den Zeiten vor der Erfindung von Taschenrechner und Computer nahmen Wissenschaftler Logarithmen zu Hilfe, um langwierige Rechnungen zu verkürzen. Benford fiel eines Tages auf, dass die ersten Seiten seiner Logarithmentafel, auf denen die Zahlen mit einer kleinen Ziffer an führender Stelle standen, verschmutzter war als die hinteren. Daraus folgerte er, Zahlen mit einer 1 am Anfang kämen häufiger vor als solche mit einer 2 vorne und die wiederum öfter als solche mit einer 3 zu Beginn. Denn nur so waren die zerfledderten ersten Seiten des Nachschlagewerks zu erklären.
Benford beließ es nicht bei den Logarithmen. Er stürzte sich auf alles Zahlenmaterial, das er bekommen konnte: Halbwertszeiten radioaktiver Elemente, Primzahlen, Stromrechnungen, Todesraten, physikalische und chemische Konstanten, Ergebnisse der Baseball-Liga, Hausnummern amerikanischer Wissenschaftler. Benfords Fleiß war grenzenlos. Insgesamt analysierte er – ohne Computer – mehr als 20.000 Datensätze. Fast überall ergab sich dasselbe Bild: An der ersten Stelle kam am häufigsten die 1, gefolgt von den anderen Zahlen in aufsteigender Ordnung.
Natürlich befolgen nicht alle Datensätze Benfords Regel. Die Tageshöchsttemperaturen im Sommer etwa beginnen fast alle mit 2 oder 3. Auch Lottospielern bringt das Gesetz nichts, da die Kugeln mit den Nummern 10 bis 19 nicht häufiger aus der Trommel fallen als die anderen.
Woran die Häufung der kleinen Ziffern an der höchsten Stelle liegt, haben die Wissenschaftler noch nicht vollständig verstanden. So gibt es bislang kein allgemein gültiges Kriterium, um im Voraus zu entscheiden, ob ein Datensatz Benfords Gesetz gehorcht oder nicht. Die einzige Möglichkeit, das herauszukriegen, ist, die Zahlen mit einer 1 vorne zu zählen, die mit einer 2 und so weiter.
Bei Hausnummern zum Beispiel ist es klar, warum die kleinen Ziffern an der führenden Stelle bevorzugt erscheinen. Jede Straße beginnt mit der Nummer 1, aber nicht alle erreichen die 10. Alle Straßen mit zweistelligen Hausnummern haben – sieht man einmal von Baulücken ab – Adressen in den Zehnern, aber nur manche davon in den Neunzigern. Und Nummern über 500 sind extrem selten, während Hausnummern zwischen 100 und 199 öfter auftreten. Daher kommt die 1 als führende Ziffer am häufigsten vor.
Bei Aktienkursen ist Benfords Gesetz ebenfalls nachzuvollziehen. Angenommen ein Aktienindex beträgt 1000. Damit die 2 die 1 als führende Ziffer ablöst, müsste der Index um 100 Prozent, nämlich von 1000 auf 2000 steigen. Legt er jährlich um 10 Prozent zu, dauert das etwas mehr als sieben Jahre. Beträgt der Aktienindex aber 5000, genügt ein Anstieg um 20 Prozent, um die 5 durch die 6 zu verdrängen. Bei gleichbleibendem Wachstum von 10 Prozent hält sich die 5 als führende Ziffer daher nur knapp zwei Jahre. Startet der Index bei 9000, fehlen ihm nur 11 Prozent oder gut 13 Monate bis zu 10.000. Nun beginnt der Aktienindex erneut mit einer 1 – bis er wieder um 100 Prozent angestiegen ist.
In jüngster Zeit prüften Forscher mit dieser Regel, ob politische Wahlen manipuliert worden seien. Die Stimmenzahlen bei den Präsidentschaftswahlen 2004 in Venezuela, 2006 in Mexiko und 2009 im Iran wichen demnach deutlich von Benfords Muster ab. Andere Experten bezweifeln jedoch, ob sich so Wahlbetrug nachweisen lässt.
Steuerbetrug könnte sich hingegen mit dem Gesetz aufdecken lassen. Die führenden Ziffern der Zahlen einer korrekten Steuererklärung oder Bilanz sollten nach Benford verteilt sein. Sind sie das nicht, hat die Angaben wahrscheinlich jemand frei erfunden. Eine anschließende detaillierte Untersuchung sollte dann für Klarheit sorgen. Auch die Manipulation der griechischen Wirtschaftsdaten vor der jüngsten Staatskrise lässt sich mit dem bizarren Gesetz belegen.
Mit Computern können Mathematiker nicht nur ihre Formeln attraktiv darstellen. Zuweilen helfen die Elektronenhirne ihnen auch, Sätze zu beweisen. Klassisches Beispiel ist das Vierfarbenproblem. 1852 wollte der Student Francis Guthrie (1831–1899) eine Landkarte der englischen Grafschaften kolorieren. Dabei fragte er sich, wie viele Farben für jede Karte genügen, damit benachbarte Länder verschiedenfarbig sind. An Hand von Beispielen stellte er fest, dass drei Farben nicht ausreichen. Andererseits konnte er keine Karte konstruieren, für die man fünf gebraucht hätte. Kommt man in jedem Fall mit vier aus?
Trotz zahlreicher Bemühungen konnte über hundert Jahre lang niemand die Vermutung beweisen, dass vier Farben genügen, noch sie widerlegen. Das Vertrackte an dem Problem: Selbst wenn man geprüft hat, dass für Millionen von Landkarten jeweils vier Farben reichen, hilft einem das nicht weiter. Es könnte immer noch jemand eine weitere Karte finden, die eine fünfte Farbe benötigt. Gefordert war ein Beweis, der alle Fälle abdeckt.
1970 führte Wolfgang Haken (*1928), Emeritus an der Universität von Illinois (USA), das Problem auf eine Liste von Situationen zurück, in denen vier Farben möglicherweise nicht ausreichen. Dummerweise war die Liste so umfangreich, dass der gebürtige Berliner sie nicht mit Bleistift und Papier abarbeiten konnte. Deswegen überlegte er, es mit dem Computer zu probieren. Doch sah es so aus, als ob der Rechner mehr als hundert Jahre damit beschäftigt wäre.
Haken tüftelte daher mit seinem Kollegen Kenneth Appel (1932–2013) daran, eine Software zu entwerfen, die die kritischen Karten schneller durchprobieren könnte. Haken und Appel schreiben dazu: »Das Programm begann, uns zu überraschen. Zu Beginn überprüften wir seine Überlegungen von Hand, damit wir immer vorhersagen könnten, wie es sich in einer Situation verhalten würde; dann aber verhielt es sich plötzlich wie ein Schach-Computer. Es erarbeitete komplizierte Strategien, die alle die Tricks verwendeten, die wir ihm beigebracht hatten, und oft waren diese Ansätze viel gescheiter als jene, die wir ausprobiert hatten.«
1977 hatte der Computer alle 1936 Karten auf der Liste durchgeackert. Für keine waren mehr als vier Farben notwendig. Damit war der Vierfarbensatz bewiesen.
Haken und Appel reichten ihren Beweis bei einer mathematischen Fachzeitschrift ein. Wie bei Forschungsarbeiten üblich, schickten die Herausgeber ihn zur Begutachtung an andere Spezialisten für das Problem. Die prüften nicht nur den theoretischen Teil der Arbeit, sondern wiederholten auch die Computerrechnungen, ohne eine Unstimmigkeit zu finden. Dennoch gab es nach der Veröffentlichung Diskussionen, ob die Abhandlung von Haken und Appel als Beweis gilt. Niemand könne jeden Schritt nachvollziehen, den der Rechner durchführt, argumentierten Skeptiker. Deswegen sei es nicht auszuschließen, dass sich ein Fehler eingeschlichen habe.
Andere hielten entgegen, auch bei Beweisen ohne Computerhilfe blieben Inkorrektheiten oft unentdeckt. In der Tat hatte es schon viele Fälle gegeben, in denen erst Jahre später logische Lücken entdeckt wurden. Allein in der Geschichte des Vierfarbensatzes passierte das mehrfach. Ein »Beweis« hatte elf Jahre Bestand, bevor er sich als ungültig herausstellte.
Für andere Theoreme hatten Wissenschaftler so umfangreiche Beweise ersonnen, dass sie ein Einzelner nicht mehr komplett verifizieren kann. Die Klassifikation der endlichen Gruppen etwa war 1992 das Gemeinschaftswerk von mehr als hundert Mathematikern. Dennoch gilt das Problem als erledigt, da jeder Beweisschritt von mehreren Fachleuten nachvollzogen wurde.
Mitte der neunziger Jahre wollten vier amerikanische Mathematiker Haken und Appels Beweis durchgehen. Bald bemerkten sie, dass es einfacher sei, die Vermutung neu zu beweisen, als deren Manuskript zu verstehen. Das Ergebnis war ein neuer Beweis des Vierfarbensatzes, der zwar auch auf den Computer zurückgreift, aber wesentlich leichter verständlich ist. »Wir haben weder überprüft, ob der Computer korrekt arbeitet, noch, ob das Übersetzungsprogramm fehlerlos ist«, räumen die Autoren ein. Da bei mehreren Durchläufen immer dasselbe Ergebnis herauskam, sei die Wahrscheinlichkeit, dass etwas nicht stimme, »unendlich kleiner« als die eines menschlichen Fehlers.
Mit der Zeit akzeptierten immer mehr Mathematiker Beweise, die mit Hilfe von Elektronenhirnen geführt wurden. Zumal neben dem Vierfarbensatz andere Theoreme aufkamen, die sich anscheinend nur auf diese Art beweisen ließen.
Ästheten sind aber nach wie vor unzufrieden mit den Computerbeweisen. Sie bemängeln, sie seien zu technisch und brächten keine Einsicht in die Struktur eines Problems. »Ein guter Beweis liest sich wie ein Gedicht«, lautet ein Credo der Zunft. Der des Vierfarbensatzes sehe dagegen aus wie das Telefonbuch. Nach einem eleganten Beweis wird weiter gesucht.
Schönheit gilt in der reinen Mathematik als eines der höchsten Güter. Am eindrücklichsten formulierte das der Engländer Godfrey Harold Hardy (1877–1947): »Die Werke des Mathematikers müssen schön sein wie die des Malers oder Dichters. Die Ideen müssen harmonieren wie die Farben oder Worte. Schönheit ist die erste Prüfung: Es gibt keinen Platz in der Welt für hässliche Mathematik.«
Was die Schönheit eines mathematischen Gedankens ausmacht, ist nicht klar definiert. Für den Uneingeweihten ist es nur schwer nachzuvollziehen.
Eine Ahnung von mathematischer Schönheit vermitteln die Methode von Gauß, die ersten hundert Zahlen zusammenzuzählen, der Beweis des Satzes von Pythagoras oder Euklids Beweis der Unendlichkeit der Primzahlen. Für den ungarischen Mathematiker Paul Erdös (1913–1996) stellte Letzterer ein Schlüsselerlebnis dar: »Als ich zehn war, erzählte mir mein Vater vom Euklidischen Beweis, und ich hatte angebissen.« Mit 17 Jahren bewies er dann, dass es zwischen jeder beliebigen Zahl und ihrem Doppelten mindestens eine Primzahl gibt. Zwischen 3 und 6 etwa liegt die 5, zwischen 10 und 20 die 11. Aber auch zwischen einer Billiarde und zwei Billiarden muss sich dem Theorem zufolge eine Primzahl befinden. Erdös bewies die Behauptung zwar nicht als erster, aber auf viel einfachere Weise als seine Vorgänger.
Das höchste Ziel des Ungarn war es, mathematisch elegante Beweise zu finden. Fast 60 Jahre seines Lebens verbrachte er damit, durch die Welt zu reisen, Kollegen zu besuchen und mit ihnen neue Theoreme aufzustellen. Einen festen Wohnsitz hatte er nicht. Mit sich führte er seinen ganzen Besitz: einen Koffer mit ein paar Klamotten und eine Einkaufstasche voller Manuskripte. »Mein Geist ist offen«, pflegte er zur Begrüßung zu sagen, was so viel bedeutete wie: »Ich bin bereit für neue mathematische Abenteuer«. Ohne in seinen Augen überflüssige Höflichkeitsfloskeln sprach er häufig bereits im nächsten Satz ein mathematisches Problem an. Kein Mathematiker hat so viele wissenschaftliche Abhandlungen veröffentlicht wie er. Und keiner hat jemals mit mehr Kollegen zusammen geforscht. Mit knapp 500 Mathematikern hat Erdös gemeinsame Arbeiten geschrieben. Ein Rekord, der kaum zu brechen ist.
Erdös erzählte gerne von dem BUCH, in dem Gott die perfekten Beweise für Theoreme aufbewahre. Gott, an den er selbst gar nicht glaubte, war für ihn nur der SF: supreme fascist (oberster Faschist). Die Menschen habe der SF nur erschaffen, damit er sich an ihrem Leiden erfreuen könne. Eine seiner Grausamkeiten sei es, ihnen das BUCH vorzuenthalten. So müssten Mathematiker ihre geballte Intelligenz und Intuition aufbieten, um ab und zu mal einen kleinen Blick hineinwerfen zu dürfen.
Die Berliner Mathematiker Martin Aigner (*1942) und Günter Ziegler (*1963) schlugen ihrem vagabundierenden Kollegen vor, gemeinsam eine erste Annäherung an das BUCH zu verfassen. Der nahm die Idee begeistert auf und machte sich – ganz wie es seine Art war – sofort an die Arbeit. Seite um Seite kritzelte er mit Vorschlägen voll.
Bevor das Werk fertig wurde, starb Erdös 1996. Wie es sich für ihn gehörte, hatte der 83-Jährige damals gerade an einer Tagung über Mathematik in Warschau teilgenommen. Aigner und Ziegler vollendeten »Das BUCH der Beweise« ohne ihn.
Die Autoren haben zwar versucht, vor allem elementare Beweise vorzuführen. Doch Normalsterbliche, die weder ein paar Semester Mathematik studiert haben noch über den Genius eines Paul Erdös verfügen, werden bei der Lektüre ins Straucheln geraten. Der Meister selbst freilich hätte seine helle Freude an diesem Feuerwerk mathematischer Geistesblitze gehabt.
Im BUCH der Beweise steht der euklidische Beweis an erster Stelle, gefolgt von fünf weiteren Beweisen, dass es unendlich viele Primzahlen gibt. Primzahlen sind vergleichbar mit den Elementen in der Chemie oder den Elementarteilchen in der Physik. Ein Molekül Wasser besteht aus zwei Atomen Wasserstoff und einem Atom Sauerstoff. Ähnlich lässt sich jede Zahl aus Primzahlen zusammensetzen. 30 zum Beispiel ist das Produkt von 2, 3 und 5. Noch heute spielen Primzahlen in der Forschung eine wichtige Rolle. Längst nicht alle ihre Eigenschaften sind entdeckt. Etliche Seiten in Gottes BUCH, die noch nicht von Menschenhand rekonstruiert sind, handeln vermutlich davon.
So genial sich Erdös zeigte, war er in weltlichen Dingen eher unbeleckt. Er selbst schildert ein Erlebnis, das er als 21-Jähriger hatte: »Es war Teezeit, und es wurde Brot gereicht. Ich war viel zu verwirrt, um zuzugeben, dass ich mir noch nie ein Brot geschmiert hatte. Ich versuchte es, und es war gar nicht so schwer.« Zeit seines Lebens lernte der Junggeselle nicht einmal, die einfachsten Arbeiten im Haushalt zu verrichten. »Ich könnte wahrscheinlich ein Ei kochen, aber ich habe es nie probiert«, gab er einmal zu. Das hätte ihn nur Zeit gekostet, in der er lieber neue Theoreme suchte, um sie anschließend elegant zu beweisen – und so einen kurzen Blick in Gottes BUCH zu erhaschen.
Erdös schlief selten mehr als fünf Stunden und hielt sich mit Kaffee und Aufputschmitteln wach. »Ein Mathematiker ist eine Maschine, die Kaffee in Theoreme umwandelt«, sagte er. Einmal bot ein Freund eine Wette um 500 US-Dollar an, ob er es schaffen würde, 30 Tage ohne Drogen zu leben. Er hielt durch, meinte aber, die Wette habe die Mathematik um einen Monat zurückgeworfen.
Paul Erdös verfasste rund 1500 mathematische Arbeiten, die meisten davon zusammen mit Kollegen. Daraus entstand die Erdös-Zahl: Die 509 Mathematiker, die direkt mit ihm veröffentlicht haben, besitzen die Erdös-Zahl 1, diejenigen, die nicht mit ihm persönlich, aber mit jemandem mit der Erdös-Zahl 1 zusammengearbeitet haben, die Erdös-Zahl 2 und so weiter. Akribisch werden die Listen im Internet geführt (http://www.oakland.edu/enp/).
Die zehn schönsten Theoreme
Im Jahr 1990 veranstaltete die Zeitschrift »Mathematical Intelligencer« (Mathematischer Informant) eine Umfrage unter ihren Lesern, was die schönsten Theoreme seien. Dabei ging es nicht um die Beweise oder etwaige Anwendungen, sondern nur um die Ästhetik der Aussagen. Unter den Top Ten finden sich vier Sätze, die in diesem Buch erwähnt sind. Auf Platz 9 landete der Vierfarbensatz, auf Platz 7 das Theorem, nach dem die Quadratwurzel aus 2 nicht als Bruch darzustellen ist, auf Platz 4 der Satz »Es gibt nur fünf platonische Körper« und auf Platz 2 Euklids Unendlichkeit der Primzahlen.
Als schönsten Satz wählten die Mathematiker die Formel eiπ+1 = 0. In der Gleichung tauchen die wichtigsten Zahlen der Differentialrechnung auf: 0, 1, die sogenannte Eulersche Zahl e (=2,718…), die Kreiszahl π (=3,141…) und die sogenannte imaginäre Einheit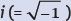 
.
Das indische Genie
Srinivasa Ramanujan (1887–1920) genoss nie eine universitäre Ausbildung. Mathematik brachte er sich selbst mit Büchern bei. Im Alter von 26 Jahren schrieb der Inder als Angestellter im Hafenamt an den bekannten Zahlentheoretiker Godfrey Hardy. Dem Brief fügte er neun Seiten voller Gleichungen und Formeln bei – ohne eine einzige davon zu beweisen.
Hardy sah sie sich an und kam zu dem Schluss: »Sie müssen wahr sein. Denn wären sie es nicht, hätte niemand die Vorstellungskraft, sie sich auszudenken.« An Ramanujan schrieb er: »Ich wünsche mehr … und Beweise, sobald wie möglich!« Überdies lud er ihn nach England ein. Der Inder hatte aber Bedenken als gläubiger Hindu und Angehöriger der Brahmanen-Kaste ins Ausland zu reisen. Als er sich drei Tage und Nächte im Tempel der Hausgöttin Namagiri aufhielt, hatte er jedoch eine Vision. Die Göttin sagte ihm: »Fahr nach Europa – brich mit der Tradition.«
In Cambridge ersann er eine Formel nach der anderen. »Eine Gleichung hat für mich keinen Sinn, es sei denn, sie drückt einen Gedanken Gottes aus«, lautete sein Motto. Teilweise arbeitete er 30 Stunden ohne Unterbrechung, was seine angeschlagene Gesundheit nicht gerade beförderte.
Einmal besuchte Hardy seinen Schützling, als dieser im Krankenhaus lag. Um das Gespräch aufzunehmen, erzählte der Zahlentheoretiker, er sei mit dem Taxi Nummer 1729 gekommen, eine offensichtlich langweilige Zahl. Ramanujan widersprach sofort. 1729 sei die kleinste Zahl, die sich auf zwei verschiedene Arten als Summe von zwei dritten Potenzen schreiben ließe: 1729 = 13 + 12 = 93 +103.
Die Aufzeichnungen des Inders Srinivasa Ramanujan stellen Mathematiker noch heute vor Rätsel.
Nach fünf Jahren in England kehrte Ramanujan 1919 nach Indien zurück. Ein Jahr später starb er im Alter von 32 Jahren an Tuberkulose. Er hinterließ vier schwarze Notizbücher, vollgekritzelt mit Formeln ohne Beweise. Noch heute rätseln die Mathematiker über manche davon.
Viele Mathematiker haben wie Erdös ihre Besonderheiten. Pierre de Fermats Unart war es, Kommentare an den Rand von Buchseiten zu kritzeln. So schrieb er Mitte des 17. Jahrhunderts eine Vermutung, die berühmt werden sollte, in ein Werk des Diophant über Gleichungen mit ganzzahligen Lösungen. Wie um die Nachwelt zu verspotten, ergänzte er: »Für diese Behauptung habe ich einen wahrhaft wunderbaren Beweis gefunden, aber dieser Rand ist zu schmal, um ihn zu fassen.« Veröffentlicht hat diesen Satz erst posthum sein Sohn. Den wahrhaft wunderbaren Beweis nahm Fermat mit ins Grab.
Fermat hatte behauptet, die Gleichung xn + yn = zn habe für n größer als 2 keine ganzzahligen Lösungen. Dass sie für n = 2 welche hat, wussten schon die Babylonier. In diesem Fall ist die Gleichung der Satz des Pythagoras und eine mögliche Lösung lautet 32 + 42 = 52. Doch für n = 3, 4 oder mehr lässt sich laut Fermat keine solche Lösung finden.
Zwar bewiesen Mathematiker im Lauf der Zeit zum Beispiel, dass die Gleichung x + y = z keine ganzzahligen Lösungen besitzt, doch für beliebige Hochzahlen (Exponenten) größer als 2 wollte der Nachweis einfach nicht gelingen.
Anfang des Jahrhunderts lobte Paul Wolfskehl (1856–1906) einen Preis aus für denjenigen, der Fermats Vermächtnis aufklärt. Der Grund dafür war Liebeskummer. Der deutsche Industrielle hatte sich von seiner Angebeteten einen Korb geholt und beschlossen, seinem Leben ein Ende zu setzen. Als pedantischer Mensch hatte er geplant, sich genau um Mitternacht eine Kugel in den Kopf zu schießen. Nachdem er bereits vorzeitig alles geregelt hatte, wollte er sich zum Zeitvertreib in seinen letzten Stunden mit Fermats Vermutung befassen. Über der Mathematik vergaß er die Zeit, sein selbst gesetzter Termin verstrich und er ließ vom Selbstmord ab. Als Dank rief er den Preis in Höhe von 100.000 Goldmark ins Leben. Doch sollte es bis zum Ende des Jahrhunderts dauern, bis ihn jemand abholen konnte. Durch die zwischenzeitlichen Wirtschaftskrisen war sein Wert allerdings drastisch auf rund 35.000 Euro gefallen.
Wiles über seinen Beweis der Fermatschen Vermutung: »Ich war von diesem Problem besessen, dass ich acht Jahre lang an nichts anderes dachte – vom Aufstehen bis zum Schlafengehen. Diese ganz besondere Odyssee ist nun vorbei, und meine Seele zur Ruhe gekommen.«
Andrew Wiles (*1953) war bereits als Schulkind gebannt von Fer-mats Vermutung. Doch stellte der gebürtige Brite Beweisversuche vorerst zurück und machte Karriere als Hochschulmathematiker. Um das Jahr 1990 herum begann er, sich vom akademischen Leben zurückzuziehen und sich auf seinem Dachboden zu verschanzen. Kollegen lästerten schon, er sei wohl »ausgebrannt«. Ohne jemandem davon zu verraten, beackerte Wiles indes die berühmte Vermutung. Er hatte erfahren, dass andere Mathematiker Fortschritte erzielt und den berühmten Satz auf die sogenannte Taniyama-Shimura-Vermutung zurückgeführt hat-ten. »Ich war ganz aus dem Häuschen«, erinnert sich der Brite, der seit 2011 an der Universität Oxford forscht. Ihm sei klar geworden, »dass sich der Lauf meines Lebens ändern würde. Denn um Fermats letzten Satz zu beweisen, musste ich jetzt nur die Taniyama-Shimura-Vermutung bestätigen. Aus einem Kindheitstraum war etwas geworden, woran ein ernstzunehmender Mensch arbeiten konnte. Ich durfte die Gelegenheit nicht verpassen.«
Sieben Jahre später schließlich konnte Wiles tatsächlich einen Beweis präsentieren, der auf den neuesten Entwicklungen der Mathematik aufbaute. Die Fachwelt stand Kopf und selbst in den Medien, die sonst nicht gerade häufig über Mathematik berichten, avancierte er zum Star.
Doch schien das Drama seinen Lauf zu nehmen, als ein Kollege eine Lücke in Wiles’ Argumentationen entdeckte. Doch binnen eines Jahres konnte er zusammen mit seinem Doktoranden Richard Taylor (*1962) das Loch stopfen. Seitdem gilt die berüchtigte Vermutung als bewiesen. 1997 nahm Wiles den Wolfskehl-Preis in Empfang.
Eine Vermutung von Johannes Kepler blieb mit 389 Jahren noch länger offen als die von Fermat. Der deutsche Astronom hatte überlegt, wie sich Kugeln möglichst dicht stapeln lassen. Anlass dazu waren die Kerne eines Granatapfels, die sehr dicht beieinander liegen. 1609 kam er in seinem Buch »Vom sechseckigen Schnee« über in der Natur auftretende Muster zu dem Schluss, dass Heer und Marine die Lösung bereits kannten. Platzsparender, als die Soldaten ihre Kanonenkugeln lagerten, behauptete er, gehe es nicht.
Der Aufbau ist ebenso simpel wie effizient: An zwei nebeneinander liegende Kugeln legt man eine dritte so, dass sie die beiden anderen berührt. Die nächsten Geschosse bekommen ebenfalls jeweils Kontakt zu zwei bereits hingelegten. Ist die Fläche bedeckt, geht es an die zweite Schicht, die genauso aussieht wie die erste. Die Kugeln rutschen dabei von selbst in Position, nämlich in die Lücken der unteren Lage. So lässt sich Schicht auf Schicht fügen. Der Anteil Eisen am Gesamtvolumen beträgt bei dieser Anordnung rund 74,048 Prozent (genau: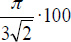 
Prozent). Diese Stapeltechnik kann man auf dem Markt bewundern, wenn Obsthändler ihre Orangen zu kunstvollen Pyramiden auftürmen.
Immer wieder behaupteten Mathematiker, sie hätten bewiesen, dass diese Anordnung optimal sei. Doch jedes Mal fanden kritische Kollegen Lücken in der Argumentation. 1998 meldete Thomas Callister Hales (*1958) vorsichtig an, er habe es möglicherweise geschafft – wenn nicht die scientific community auch bei ihm einen Fehler fände. »Dieses Gebiet der Mathematik ist berüchtigt für seine falschen Beweise«, erklärte der Mathematiker von der Universität im amerikanischen Pittsburgh. »Ich verbrachte mehrere Monate damit, die Arbeit zu prüfen.« Insgesamt umfasst der Beweis mehr als 250 Seiten Text und über drei Gigabyte (Milliarden Byte) Programme und Daten.
Ein Gremium, das den Beweis begutachten sollte, gab nach Jahren auf. Die zwölf Mitglieder wollten sich nicht vollkommen festlegen, ob der Beweis stimmt und verkündeten, zu 99 Prozent sei er korrekt. Der Herausgeber der Zeitschrift, die Hales’ Beweis veröffentlichte, schrieb an ihn: Die Gutachter »sind nicht in der Lage, die Richtigkeit des Beweises festzustellen, und werden auch in Zukunft dazu nicht in der Lage sein. Sie sind mit ihrer Energie am Ende.« Ein Novum in der Mathematik, in der so viel Wert auf gesicherte Erkenntnisse gelegt wird.
Ähnlich wie bei Fermats Satz galt es bei der Keplerschen Vermutung, zu beweisen, dass es etwas nicht gibt – bei Fermat waren es ganzzahlige Lösungen gewisser Gleichungen, bei Kepler Kugelpackungen, die den Raum zu mehr als 74,048 Prozent ausfüllen. Schon allein das machte die Aufgabe schwierig. Überdies können in kleinen Gebieten die Kugeln sehr wohl dichter liegen. Doch zwingen solche Anordnungen die Kugeln drum herum in ungünstigere Positionen, was den lokalen Dichtevorteil wieder aufzehrt.
Um das zu beweisen, wies Hales zunächst nach, dass es genügt, Haufen aus höchstens 53 Kugeln zu betrachten statt unendlich große Haufen. Mit Hilfe eines Doktoranden und eines Computers arbeitete er sodann die 5000 verbleibenden Typen von Kugelhaufen ab.
Anders als Wiles, der still und heimlich auf seinem Dachboden über Fermats Vermutung brütete, stellte Hales einen Forschungsplan auf seine Homepage, der in fünf Schritten zum Beweis der Keplerschen Vermutung führen sollte. »Ich kündigte das Programm an, weil ich andere dazu anstiften wollte, mir zu helfen«, berichtet er. »Ich fühlte mich oft von der Größe des Problems überwältigt.«
Nachdem Thomas Hales bewiesen hatte, wie man Kugeln (und somit auch Apfelsinen) optimal stapelt, bekam er einen Anruf vom örtlichen Markt: »Kommen Sie gleich vorbei. Wir können zwar Orangen stapeln, aber wir haben Probleme mit den Artischocken.«
Zum Schluss habe er durchgehend über der Kepler-Vermutung gebrütet, unterbrochen nur von kurzen Pausen zum Schlafen und Essen. Als der Beweis vollbracht war, sei er dann in eine Leere gefallen. Womit einer wie er die füllt? Natürlich mit der nächsten harten Nuss. William Thomson (1824–1907), besser bekannt als Baron Kelvin, fragte sich im 19. Jahrhundert, wie man den Raum so in gleiche Volumina teilen könne, dass deren Oberflächen minimal seien. »Das Kelvin-Problem hat alle Merkmale eines guten Problems«, findet Hales. »Es lässt sich leicht formulieren, hat eine reiche Geschichte, und ist so schwierig, dass ich wette, es dauert mehr als eine Generation, bis es gelöst ist.«
Der komplizierte Beweis der Kepler-Vermutung ließ dem amerikanischen Mathematiker ebenfalls keine Ruhe. Er startete das Projekt »Flyspeck« (Fliegendreck oder minutiöse Überprüfung, kurz FPK wie »formal proof of Kepler«), um seine Arbeit mit einer speziellen Software zu überprüfen. Dank der Mithilfe eines großen Teams konnte er 2014 verkünden, dass die Verifikation vollbracht sei. Fachgutachter seien nun »nicht mehr länger nötig«, meint Hales. Ihm sei eine große Last von den Schultern gefallen: »Ich fühle mich plötzlich zehn Jahre jünger.«
