© Springer Nature Switzerland AG 2019
Eric Luiijf, Inga Žutautaitė and Bernhard M. Hämmerli (eds.)Critical Information Infrastructures SecurityLecture Notes in Computer Science11260https://doi.org/10.1007/978-3-030-05849-4_16

Discovering Vulnerabilities in Heterogeneous Interconnected Systems

Luca Faramondi1  , Gabriele Oliva1  , Stefano Panzieri2   and Roberto Setola1  
(1)
Campus Bio-Medico University, Via Álvaro del Portillo 2, 00128 Rome, Italy
(2)
University Roma Tre, Via della Vasca Navale 79, 00146, Rome, Italy
 
 
Luca Faramondi (Corresponding author)
Email: l.faramondi@unicampus.it
 
Gabriele Oliva
Email: g.oliva@unicampus.it
 
Stefano Panzieri
Email: panzieri@uniroma3.it
 
Roberto Setola
Email: r.setola@unicampus.it

Abstract

The identification of vulnerabilities in critical infrastructure networks, especially in the event of an intentional attack, is a fundamental task to comprehend the behavior of such networks and to implement protection strategies with the purpose of raising their robustness and resilience. In this work, we characterize the network vulnerability with respect to an attacker that aims at destroying subsystems in a way that guarantees, at the same time, the maximization of the damage dealt and the minimization of the effort spent in the attack. To this end, we follow a topological approach and we characterize each subsystem as a node, while dependencies are modeled in terms of a directed edges. Moreover, each node is characterized by an intrinsic degree of importance and by the effort required to attack it. Such a differentiation of the nodes allows to capture the heterogeneous essence of the different subsystems in a Critical Infrastructure network. In this setting, we model the damage dealt by the attacker in terms of a weighted version of the pairwise connectivity, where the weights correspond to the nodes’ importance; moreover we model the overall attack effort in terms of the effort required to attack the nodes. The proposed methodology aims at computing a criticality metric based on a multi-objective optimization formulation. Specifically, the criticality metric represents the frequency with which a given subsystem is attacked in the hypothetical attack plans belonging to the Pareto front. Finally, we complement our methodology by introducing upper and lower bounds on the overall attacker’s effort, in order to specialize the proposed methodology to different classes of attackers. The feasibility of the proposed solution is tested on the US Airline Network as in 1997.

Keywords

Critical infrastructureConnectivity measureCritical nodes

1 Introduction

Due to the large number of natural and malicious events that may affect Critical Infrastructures, improving the robustness and resilience of such systems is a fundamental task. In this view, due to budget limitations (in terms of required effort), it is mandatory to identify the most critical elements of an infrastructure, in order to properly organize the available protection resources. In the last few years, the scientific community has been increasingly interested in developing effective strategies to identify the most critical elements of an infrastructure network (see, among others, [10, 11]). A large fraction of the proposed methods identifies criticality subsystems in terms of their interconnection with the other subsystems, i.e., according to a topological perspective. Specifically, a typical approach is to study the degradation of important network parameters, such as node degree, clustering coefficient, or betweenness, upon iterative removal of nodes and/or edges, thus simulating the robustness/resilience of the network with respect to intentional attacks or natural disasters [12]. Moreover, existing literature does not make particular distinction among the particular nodes, i.e., they assume that the topological parameters completely describe the robustness/resilience of the network after an adverse event, irrespectively of which pairs of nodes are actually connected by a direct link or by a path. If such an assumption is legitimate for particular networks (e.g., for a power grid, where any node might be able to provide power to the nodes connected to it by a path), it seems less justified in other sectors, such as telecommunications or transportations, where nodes might have highly heterogeneous characteristics.

Among other descriptors of network connectivity, the pairwise connectivity (PWC) [9] represents a popular metric, it that it explicitly measures the number of pairs of nodes in the network that are connected via a path. By leveraging on the PWC metric, the identification of the critical nodes is typically done by solving the so-called Critical Node Detection Problem (CNP) [6–8], which aims at identifying which nodes should be attacked (up to a given limit k) in order to create the largest possible degradation. Such an approach, however, typically requires a large number of Boolean decision variables [7] and a number of constraints that can be non-polynomial in the number of nodes of the network [8]; these factors may limit the applicability of the standard CNP methodology.

Notice that the CNP problem typically introduces some a priori hypothesis on the attack, e.g., the number of attacked nodes is upper-bounded by a small integer or different constraints are introduced to narrow the otherwise overwhelming complexity of this problem. In [2] a strategy to avoid introducing such constraints is provided by adopting a multi-objective optimization perspective where each node is characterized in terms of the effort required to attack it; in particular the approach in [2] aims at identifying those nodes that, if attacked, minimize the residual network connectivity in terms of PWC and, at the same time, correspond to the minimum effort. Notably, no a priori assumption is made on the specific attack budget and number of targets.

1.1 Contribution

In this work we propose an approach that extends the one in [2] by characterizing each node not only in terms of the effort required by the attacker to target that node, but also considering the relevance or importance the node has. Also in this case, no a priori assumption on the attacker psychology is made. In more detail, while PWC assigns the same relevance to any pair of nodes connected by a path in the network after the attack, in this paper we extend such an index by considering a different relevance for different pairs of nodes, thus accounting for the degree of heterogeneity of the network. Finally, we complement our methodology by introducing upper and lower bounds on the overall attacker’s effort, in order to specialize the proposed methodology to different classes of attackers.

1.2 Paper Outline

The paper outline is as follows: In Sect. 2, for the sake of completeness, we collect some preliminary definitions. In Sect. 3 we provide the definition of our methodology by introducing a connectivity measure for heterogeneous networks and the proposed attacker model. Results and discussions are presented in Sect. 4, where a validation is carried out for a real network. Finally, some conclusive remarks are collected in Sect. 5.

2 Preliminaries

2.1 General Preliminaries

Let us denote by |X| the cardinality of a set X; moreover, we represent vectors via boldface letters, and we use $$\mathbf{k}_m$$ to indicate a vector in $$\mathbb {R}^m$$ whose components are all equal to k. We denote by $$0_{n,m}$$ an $$n\times m$$ matrix whose entries are all 0, and by $$I_n$$ the $$n\times n$$ identity matrix.

Let A be an $$n\times m$$ matrix and let B be an $$p\times q$$ matrix; the Kronecker product of A and B is the $$np\times mq$$ matrix
$$ A\otimes B=\begin{bmatrix} A_{11}B&\ldots&A_{1m}B\\ \vdots&\ddots&\vdots \\ A_{n1}B&\ldots&A_{nm}B\\ \end{bmatrix}. $$
The Hadamard product of two matrices A and B, with the same number of rows and columns, is defined as
$$A \circ B = \begin{bmatrix} A_{11}B_{11}&\ldots&A_{1n}B_{1n}\\ \vdots&\ddots&\vdots \\ A_{n1}B_{n1}&\ldots&A_{nn}B_{nn}\\ \end{bmatrix}. $$
We denote by $$X = sign(A)$$ the entry-wise sign of the matrix A, i.e., $$X_{ij}=sign(A_{ij})$$.

2.2 Graph Related Definitions

Let $$G=\{V,E\}$$ denote a graph with a finite number n of nodes $$v_i\in V$$ and e edges $$(v_i,v_j)\in E\subseteq V\times V$$, from node $$v_i$$ to node $$v_j$$. A graph is said to be undirected if $$(v_i,v_j)\in {E}$$ whenever $$(v_j,v_i)\in {E}$$, and it is said to be directed otherwise; in the following we will consider undirected graphs.

The adjacency matrix of a graph G is an $$n\times n$$ matrix A such that $$A_{ij}=1$$ if $$(v_j,v_i)\in E$$ and $$A_{ij}=0$$ otherwise.

A direct path over a graph $$G=\{V,E\}$$, starting at a node $$v_i\in V$$ and ending at a node $$v_j\in V$$, is a subset of links in E that connects $$v_i$$ and $$v_j$$, respecting the edge orientation and without creating loops.

A graph $$G = \{V,E\}$$ is connected if each node can be reached by each other node by means of the links in E, regardless of their orientation. A directed graph that has a direct path from each vertex to every other vertex is said to be strongly connected.

The out-degree of a node is defined as the number of edges directed out of the node.

2.3 Pairwise Connectivity

The pairwise connectivity (PWC) [1] of G is an index that captures the overall degree of connectivity of a graph:
$$\begin{aligned} PWC(G)=\sum _{(v_i,v_j) \in V\times V, v_i \ne v_j}{p(v_i,v_j)}, \end{aligned}$$
(1)
where $$p(v_i,v_j)$$ is 1 if the pair $$(v_i,v_j)$$ is connected via a direct path in G, and is zero otherwise. In other words, the pairwise connectivity is the number of pairs of nodes that are connected via a path over G. Noting that the maximum number of couples in a graph with n nodes is $$n(n-1)$$, the normalized pairwise connectivity (NPWC) is defined as
$$\begin{aligned} NPWC(G)=\dfrac{PWC(G)}{n(n-1)} \in [0,1]. \end{aligned}$$
(2)

Remark 1

NPWC(G) is a measure of connectivity of the graph G; in fact, it is easy to note that
$$G \text{ strongly } \text{ connected } \Leftrightarrow NPWC(G)=1.$$
When $$NPWC(G)<1$$, the graph is not strongly connected, but the larger NPWC(G) is, the more G is “close" to a strongly connected graph.

2.4 Multi-objective Optimization

In this section we briefly review the key aspects of multi-objective optimization (MOO).

Given a vector $$\mathbf{x}\in \{0,1\}^n$$ representing n decision variables, a MOO problem can be expressed as follows
$$\begin{aligned} \min f(\mathbf{x})= \min \quad [f_{ 1 }(\mathbf{x}),f_{ 2 }(\mathbf{x}),\dots ,f_{ k }(\mathbf{x})]^{ T },\quad \text{ subject } \text{ to } \mathbf{x}\in \mathcal {F}, \end{aligned}$$
(3)
where $$k \ge 2$$ and the i-th objective is given by
$$f_i(\mathbf{x}):\mathbb {R}^n \rightarrow \mathbb {R}, \quad \text{ for } i = 1,\ldots ,k,$$
while $$ f(\mathbf{x})\in \mathbb {R}^k$$ is the multi-objective function. The set $$\mathcal {F}$$ represents the set of feasible solutions for the problem at hand. Moreover, the multi-objective space is defined as
$$\mathcal {Z} = \{\mathbf{z} \in \mathbb {R}^k : \exists \,\mathbf{x} \in \mathcal {F}, \mathbf{z} = f(\mathbf{x})\}.$$
Within a MOO problem, therefore, the aim is to select a feasible solution $$\mathbf{x}$$ that minimizes at the same time all the different objectives $$f_i$$. Let us consider a solution $$\mathbf{x}^*$$ for which all the objectives $$f_i(\mathbf{x}^*)$$ are simultaneously minimized, and let us denote the associated multi-objective vector $$f(\mathbf{x}^*)$$ by $$\mathbf{z}^{id}$$. Note that, when there is no conflict among the objectives, we can solve Problem (3) by solving k scalar problems, thus obtaining $$\mathbf{z}^{id}$$ as the ideal multi-objective vector. Due to the conflicting nature of the objectives $$f_i(\mathbf{x})$$, however, it is realistic to assume that $$\mathbf{z}^{id} \notin \mathcal {Z}$$.

In most practical cases, therefore, there is a need to overcome the above naive definition of an optimal solution; a typical approach in the literature is to resort to the theory of Pareto optimality [4].

Let $$\mathbf{z}^{a}$$ and $$\mathbf{z}^{b}$$ $$\in $$ $$\mathcal {Z}$$; we say that $$\mathbf{z}^{b}$$ is Pareto-dominated by $$\mathbf{z}^{a}$$ $$(\mathbf{z}^{a} \le _P \mathbf{z}^{b})$$ if:

  • $$\mathbf{z}^{a}_i \le \mathbf{z}^{b}_i$$ for each $$i = 1,2,\ldots ,k$$ and

  • $$\mathbf{z}^{a}_j < \mathbf{z}^{b}_j$$ at least for a value of $$j \in \{ 1,\ldots , k \}$$.

A solution vector $$\mathbf{x}^{*} \in \mathcal {F}$$ is a Pareto optimal solution if there is no other solution $$\mathbf{x} \in \mathcal {F}$$ such that:
$$\begin{aligned} f(\mathbf{x}) \le _P f(\mathbf{x}^{*}). \end{aligned}$$
(4)
The Pareto front $$\mathcal {P}$$ is the set of all possible Pareto optimal solutions $$\mathbf{x}^{*}$$ for the matter at hand, while we denote by $$\mathcal {P}_f$$ the set of values $$f(\mathbf{x}^{*})$$, in the multi-objective space, which correspond to each $$\mathbf{x}^{*}\in \mathcal {P}$$.

3 Network Vulnerability Analysis

In this section we generalize the PWC indexes introducing the “weighted" PWC in order to discriminate among the different pairs of nodes and illustrate how such an index can be used in MOO-based framework to identify the most critical nodes. Moreover, we introduce a bound on the maximum budget for the attacker in order to discriminate different classes of attackers: criminal, terroristic and warfare scenario.

3.1 Weighted Pairwise Connectivity

As introduced in Sect. 2.3, the PWC and the NPWC consists of two indices able to estimate the degree of connectivity of a graph. In this section we generalize these indices in order to consider not only the number of the pairs of nodes, but also the relevance of each specific pair. To this end we introduce the weighted pairwise connectivity (WPWC).

Consider a directed graph $$G = \{V,E\}$$ and let us define $$\mathbf{w} \in \mathbb R^n$$, whose entries satisfy $$w_i>0$$ represents a measure of the relevance of the nodes (e.g. number of users, dimension of the town, etc.). We define the weighted pairwise connectivity as an extension of Eq. 1
$$\begin{aligned} WPWC(G,\mathbf{w}) = \sum _{(v_i,v_j) \in V\times V, v_i \ne v_j}p(v_i,v_j)w_iw_j. \end{aligned}$$
(5)
Analogously we define its normalized version as
$$\begin{aligned} NWPWC(G,\mathbf{w}) = \dfrac{WPWC(G,\mathbf{w})}{\sum _{(v_i,v_j) \in V\times V, v_i \ne v_j}w_iw_j}. \end{aligned}$$
(6)
According to the definition in Eq. (5), it is possible to express the WPWC in terms of the weight vector w and considering the adjacency matrix A, i.e.,
$$\begin{aligned} NWPWC(A,\mathbf{w}) = \dfrac{\mathbf{1_n^T} \left[ P \circ \left( \mathbf{w \otimes \mathbf{1_n^T} } \right) \circ \left( { \mathbf{1_n}\otimes \mathbf w^T } \right) \right] \mathbf{1_n}}{\mathbf{1_n^T} \left[ \left( \mathbf{w \otimes \mathbf{1_n^T} } \right) \circ \left( { \mathbf{1_n}\otimes \mathbf w^T } \right) \right] \mathbf{1_n}}, \end{aligned}$$
(7)
where $$P = sign(\sum _{i=1}^{n-1}{A^i})-I$$ is the $$n\times n$$ matrix whose elements $$P_{ij}$$ are equal to 1 if exists a direct path in G from i to j, 0 otherwise. The definition of matrix P derives from the results described in [3], and is based on the property that the (i, j)-th entry of the k-th power of the adjacency matrix is equal to the number of paths of length k among the nodes $$v_i$$ and $$v_j$$.

3.2 Critical Nodes Detection

Let us consider a set of n heterogeneous interdependent systems, modeled as a directed graph $$G = \{V,E\}$$ whose nodes $$v_i$$ represent the subsystems and each link in E consists of an interdependence relation among them.

Moreover, consider a vector $$\mathbf{w} \in {\mathbb R^n} $$; each entry $$w_i$$ of $$\mathbf{w}$$ represents the degree of importance of the i-th subsystem. Let us also define a vector $$\mathbf{c} \in {\mathbb R^n}$$, whose elements $$c_i$$ represent the attack cost for the i-th node, i.e., an estimate of the effort required for the attacker in order to make the i-th system completely inoperable. In the following, we assume that, when the i-th system is attacked, it is removed from the network within all its incident links. The malicious attacker aims at maximizing the damage dealt to the network, i.e., to minimize the network WPWC; at the same time, he/she wants to minimize his/her effort, i.e., minimize the total attack cost. In order to distinguish among different classes of attackers, we assume that the available total budget for the attacker can be significantly different in the case he/she is a criminal, a terroristic organization or a state-sponsored terroristic organization.

These two clashing requirements (maximizing damage and minimizing attack effort) can be formulated as a MOO problem with the aim to identify the most suitable nodes to attack, which are thus those nodes that deserve increased protection by the defendant. In particular, the proposed MOO formulation reads as follows
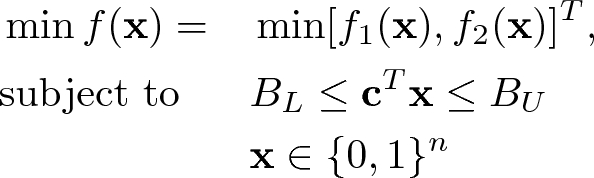
../images/477940_1_En_16_Chapter/477940_1_En_16_Equ8_HTML.png
(8)
where $$\mathbf{x}\in \mathbb {R}^n$$ is the attack vector and has entries $$x_i=1$$if the i-th subsystem is attacked, and $$x_i=0$$,otherwise. Morever, $$B_L$$ and $$B_U$$ are, respectively, the lower and upper bounds on the attack cost. Note that the upper bound $$B_U$$ can be used to discriminate different attacker classes, while the lower bound $$B_L$$ is a parameter that allows to filter non-realistic or trivial attack vectors corresponding to very limited damage/effort.
The two conflicting goals are summarized in the two following objective functions:
$$\begin{aligned} f_{ 1 } = NWPWC({\hat{A}},\mathbf{w}), \quad \quad \quad f_{ 2 } = \dfrac{\mathbf{c}^T \mathbf{x}}{\mathbf{1}^T \mathbf{c}}, \end{aligned}$$
where $$\hat{A}$$, according to the definition in Eq. (9), represents the adjacency matrix of the graph once all the incident edges to the attacked nodes have been removed from the graph (i.e. all the entries of the associated row and columns are set to 0). In other words, it holds
$$\begin{aligned} \hat{A} = A \circ (\mathbf 1_n -\mathbf x)\mathbf 1_n^T \circ ( \mathbf 1_n (\mathbf 1_n - \mathbf x)^T ) \end{aligned}$$
(9)
Due to the conflicting nature of the two objective functions, we are unable to find a unique optimal solution. To overcome such a limit, we consider all the solutions which constitute the Pareto front. Each solution that belongs to the Pareto front is characterized by an attack cost and a connectivity value as defined in Eq. 3.2. In this way, we can implicitly consider a set of multiple attackers characterized by different preferences in terms of budget and attack strategy. Thanks to the analysis of each solution in the Pareto front, we are able to determine which nodes would be optimal to attack in attack plans in spite of attackers’ preferences in terms of effects and budgets. As described in [2], we measure the frequency with which a given node is targeted in the solutions belonging to the Pareto front, and use this information to estimate the node criticality. Therefore, we adopt the node criticality index $$\chi _i$$ for a node $$v_i$$ as
$$ \chi _i=\dfrac{|\mathcal {P}_{i}|}{|\mathcal {P}|}, $$
where $$\mathcal {P}_{i}$$ is the subset of solutions in the Pareto front where node $$v_i$$ is attacked, i.e.,
$$ \mathcal {P}_{i}=\{\mathbf{x}\in \mathcal {P}\,|\, x_i=1\}. $$
while $$\mathcal {P}$$ is the set of all the solutions in the Pareto front.

The above index assigns greater criticality to those nodes $$v_i$$ that are often attacked in a solution in the Pareto front, while the criticality of a node is small if it is attacked by only a few of the solutions in the Pareto front.

4 Case Study: U.S. Airport Network

In this section we validate the proposed methodology by analyzing the US Airline Network as in 1997 [5]. The network is represented by a directed graph with 332 nodes, which represents the US airports, and direct 4252 direct edges, which represent the existence of direct flights between the airports. As described in Sect. 3, we have defined for each node $$v_i$$ of the graph a degree of importance $$w_i$$ and an attack cost $$c_i$$. Without loss of generality, we assume that the value $$c_i$$ is equal to the out-degree (i.e., the number of outgoing edges) of the i-th node. In other words, we assume that the larger the out-degree is, the higher the effort will be to disconnect the node from the network (i.e,. the attack cost is directly proportional to the number of direct flight routes from the airport to other destinations). Analogously, with respect to the definition of the importance degree, we assume that $$w_i$$ is proportional to the betweenness centrality of the i-th node. We recall that for a node $$v_i$$ the betweenness centrality is the fraction of shortest paths that pass through $$v_i$$ (without considering $$v_i$$ as source or destination of the paths). In this way, we associate a low importance to the airports with a low number of stopovers, while airports involved in high number of stopovers are considered essential for the network connectivity. For the sake of completeness, in Fig. 1, we report the distribution of out degree and betweenness centrality with reference to the analyzed network. Note that $$c_i$$ and $$w_i$$ can be estimated in different ways, e.g. $$c_i$$ may be estimated on the basis of an assessment about the actual adopted security measure, and $$w_i$$ on the base of the number of citizens living in the area of the i-th airport. In this paper we adopted the aforementioned selection because it can be estimated directly from the topology of the network.
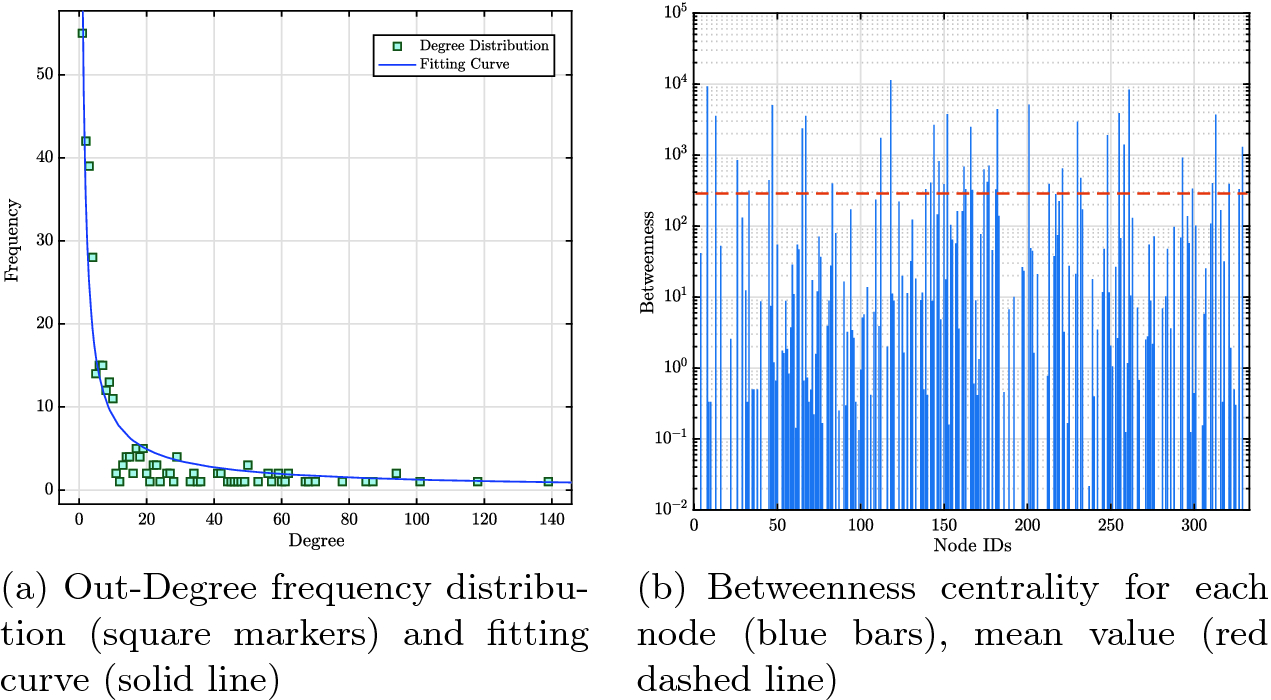
../images/477940_1_En_16_Chapter/477940_1_En_16_Fig1_HTML.png
Fig. 1.

Degree and Betweenness distributions on US Airline Network.

According to the multi-objective formulation presented in Sect. 3.2, we compute the Pareto front by using an ant colony optimization algorithm [13]. We consider three different scenarios, each one evaluated by considering $$10^6$$ generated solutions1. Specifically we consider the scenarios illustrated in Table 1 which represents different classes of attackers.
Table 1.

Attacker classes.

Class

$$B_U$$

% $$B_U^{MAX}$$

Scenario

State-sponsored organization

4252

100%

A

Terrorist group

1417

33%

B

Criminal organization

425

10%

C

In Fig. 2 we report the Pareto front of the proposed problem in the case of an attacker belonging to a state-sponsored organization. This result is obtained by considering $$B_L = 0$$ and $$B_U = 4252$$ (i.e. the upper and lower bounds on the attack cost necessary to disconnect all the nodes from the network). Note that, as illustrated in the figure, the network is completely disconnected also when a budget of just 65% of $$B_U^{MAX}$$ is used.
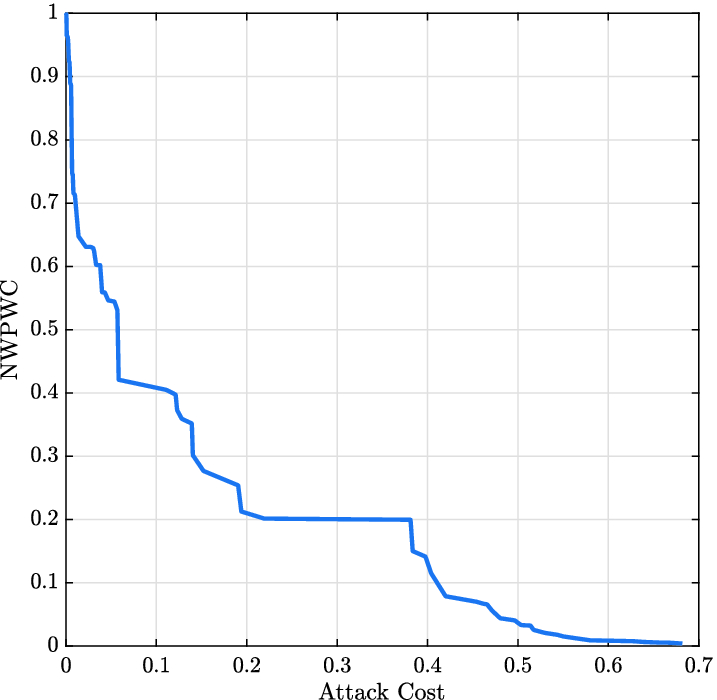
../images/477940_1_En_16_Chapter/477940_1_En_16_Fig2_HTML.png
Fig. 2.

Pareto front obtained for $$w_i$$ proportional to the node betweenness centrality measures, and $$c_i$$ proportional to the node degrees.

The Pareto front obtained via the proposed approximated technique is composed of 65 non-dominated solutions. In this view, each non-dominated solution represents a different attack plan, i.e., a different trade-off between the objectives. In order to highlight nodes that are recurrent in the different attack plans, in Fig. 3 we provide the frequency with which each node is involved in the 65 attack plans.
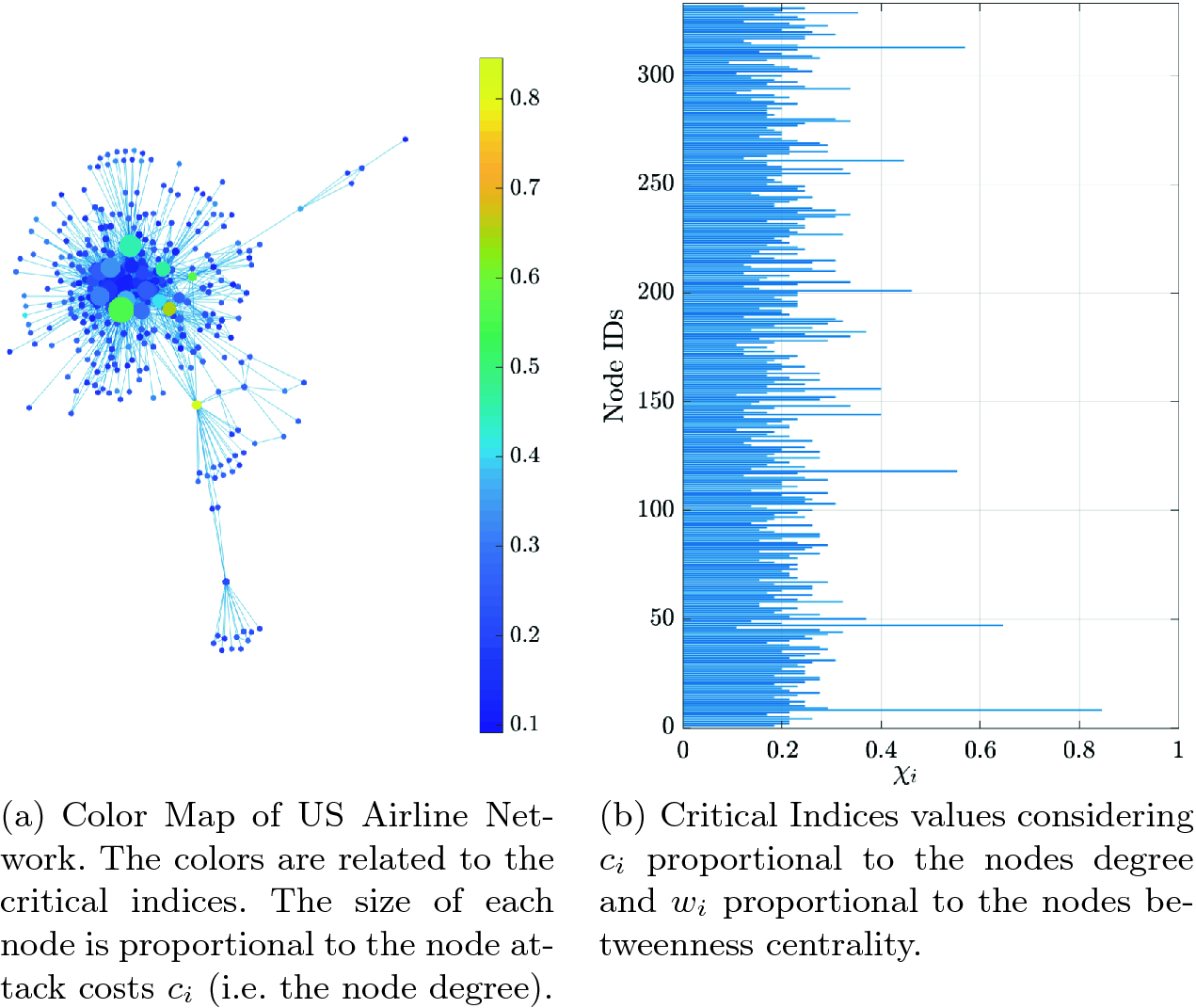
../images/477940_1_En_16_Chapter/477940_1_En_16_Fig3_HTML.png
Fig. 3.

US Airline Network vulnerability analysis.

Looking at the figure, it is evident that the most critical node is the Anchorage Airport, which is involved in 84% of the generated hypothetical attack plans (this node is characterized by an attack cost $$c_i = 29$$ and an importance degree $$w_i = 9288$$ and its deletion disconnects the graph in several connected components.). The second most critical node is Seattle-Tacoma, which is involved in 64% of the attack plans (Seatle-Tacoma has an attack cost $$c_i=57$$ and an importance degree of $$w_i=5069$$). Note that Chicago O’Hare, although having the largest importance degree $$w_i=11377$$, is involved only in 55% of the attack plans, i.e., it is ranked only fourth in terms of criticality. A reason for this lies in the high attack costs associated to it, which may imply that such an airport is too well protected and, consequently, it is not an appealing target for attackers that have limited resources. Data related to the first five most critical nodes is reported in Table 2, together with the results obtained for the other two scenarios.

In Scenario B, we consider an attacker belonging to a Terrorist Group. Terrorists, generally, can rely on considerable resources, although smaller than a Sate-like entity. Specifically, we impose, as illustrated in Table 1, an upper bound about the budget of the attacker equal to 33% of the maximum budget. Looking to Table 2 one can notice that the four most critical airports are the same as in Scenario A, but in this case they appear in considerably less attack plans (e.g., Anchorage airport is involved in only 76% of the hypothetical attack plans with respect to the 84% of Scenario A). This suggests that, in a terroristic scenario, the targets are larger hence more difficult to identify.

In the criminal organization scenario (Scenario C) one can notice that, except for the first three most critical airports (which are the same of the other scenarios), the attacker tends to neglect well protected airports (i.e., nodes characterized by an high attack cost), even with an high vulnerability (e.g., Chicago O’hare is not among the first five most critical airports).
Table 2.

Most critical Airports in US Airline Network as in 1997.

Scenario A $$B_L = 0\% $$ and $$B_U = 100\%$$

Scenario B $$B_L = 0\% $$ and $$B_U = 33\%$$

Scenario C $$B_L = 0\% $$ and $$B_U = 10\%$$

Airport

$$\chi _i$$

$$c_i$$

$$w_i$$

Airport

$$\chi _i$$

$$c_i$$

$$w_i$$

Airport

$$\chi _i$$

$$c_i$$

$$w_i$$

Anchorage

0.84

29

9288

Anchorage

0.76

29

9288

Anchorage

0.79

29

9288

Seattle-Tacoma

0.64

57

5069

Seattle-Tacoma

0.58

57

5069

Seattle-Tacoma

0.62

57

5069

Honolulu

0.56

24

3721

Honolulu

0.48

24

3721

Honolulu

0.55

24

3721

Chicago O’hare

0.55

139

11377

Chicago O’hare

0.43

139

11377

San Francisco

0.41

68

5146

San Francisco

0.46

68

5146

Dallas/Fort Worth

0.41

118

8367

Salt Lake City

0.41

59

2662

5 Conclusions

In this paper we present a novel methodology for identifying network vulnerabilities. Specifically, we formulate a multi-objective optimization problem and based on the concept of weighted pairwise connectivity, with the aim to overcome the limitations of the other formulations which consider a single class of connected nodes without differences about their relevance in the network. The proposed methodology can be used to plan the allocation of limited protection resources, with the aim to globally improve the network’s robustness. Future work will aim at applying the proposed methodology to multi-layer or hierarchical networks. Moreover, we will inspect the possibility to model the damage dealt by the attacker in terms of the reduction of flow over the network (e.g., for power or gas networks).