1 Introduction
After a number of energy supply disturbances in Europe, for example the Russian-Ukrainian natural gas dispute of January 2009, the European Commission (EC) reacted by adopting the EU Reg. 994/2010 concerning measures to safeguard security of gas supply [1]. This regulation was repealed in October 2017 by a new EU Reg. 2017/1938 concerning measures to safeguard security of gas supply [2]. For reducing security of supply consequences of potential future disruptions, the Regulation requires Member States to perform risk assessments of their gas infrastructure and establish preventive and emergency plans. Further steps contain the EC funded Connecting Europe Facility which supports trans-European networks and infrastructures in energy and other sectors.
In order to support the Regulation EC Reg 2017/1938, JRC develops a number of in-house natural gas transmission system modelling tools, ProGasNet being one of them. The ProGasNet is a versatile Matlab based probabilistic transmission gas network simulator that can be used for risk assessment, reliability and vulnerability analysis, evaluation of a new infrastructure and bottleneck analysis [3, 4]. The ProGasNet model is based on maximum flow algorithm of graph theory [7]. In order to simulate a gas crisis, a priority supply pattern of gas networks is assumed. The aim is to maximize volume of flow entering the demand nodes among functions respecting the given pipeline capacities and conserving flow over inner network elements, which might randomly fail according to the Monte Carlo sampling. A risk ratio is used for security of supply quantification of a new gas infrastructure [3]. Study of flow networks behaviour including reliability, optimisation or security of supply aspects are among popular topics in the research of infrastructure networks [8, 9].
The paper [5] was the first attempt to rank importance of the gas network elements by probabilistic measures. We used Risk Achievement (RA) similar to those used in the PSAs for ranking components (Fussell-Vesely, Birnbaum, Risk Achievement Worth, etc.…), see [10, 16].
In this paper, we evaluate an importance measure based on average gas deficit and RA for the selected attack scenarios. The security of supply results of these attack scenarios are automatically analysed, in order to obtain information, how the gas network can optimally react under various constrains (component failures) and under various (loss of) supply scenarios. Moreover, in order to evaluate security of supply consequences of a new gas infrastructure project, we compare a gas network reaction of two different infrastructure models to the attack scenarios: Model P and Model F. Model P describes a situation in the past, whereas Model F represents a future development of the gas network under the gas infrastructure project.
Thus, we can clearly quantify security of supply consequences of the new gas infrastructure project: We present a sorted list of attack scenarios with largest security of supply consequences for both models. Finally, we compare these two lists, in order to check, how the new gas infrastructure project helps to reduce the security of supply consequences of these attacks. Fortunately, majority of attacks will have smaller or close to zero security of supply consequences. However, we still detect a limited number of attack strategies with large security of supply consequences.
2 Importance Modelling for Networked Systems
Importance measures for networks are studied in the literature. The paper [11] presents two novel component importance measures for a stochastic flow network system with random edges capacities: system availability improvement potential of the component and expected unutilized capacity of the component.
The paper [12] provides two resilience-based component importance measures, which quantify the potential adverse impact on system resilience from a disruption affecting a selected link, and potential positive impact on system resilience when the selected link cannot be disrupted, respectively. Authors assume that recovery time is the same for any positive value of vulnerability.
Authors [13] present composite importance measures (CIM) for multi-state systems with multi-state components (MSMC). Experimental results show that the proposed CIM can be used as an effective tool to assess component criticality for MSMC.
The recent paper [15] includes a review on modelling of the operation of gas transmission networks in abnormal operating conditions. Novel approaches for critical infrastructure modelling and the search for the most important elements from the standpoint of system health are presented and discussed. Finally, authors suggest considering each facility whose failure to operate causes relative gas undersupply to consumers in the amount of 5% and more of the total demand for gas throughout the system as critically important. This value is substantiated by multi-iterative simulation studies and allows speaking of a small amount of potential critical facilities.
In this paper, we present a probabilistic approach for automated identification and ranking of important network elements of a European transmission gas network by ProGasNet. Moreover, in order to evaluate security of supply consequences of a gas infrastructure project, this analysis is performed twice: before and after the infrastructure project.
2.1 ProGasNet Methodology
ProGasNet is currently used for experimental simulation-based security of supply analyses of selected European gas transmission networks. Software runs well on a parallel multi-core computer, as the Monte-Carlo simulations can be independently evaluated.
We use a stochastic network representation for modelling reliability and capacity constraints of gas transmission networks. Each node and pipeline may randomly fail by a given probabilistic failure model. These component failures are sampled by the Monte-Carlo method. In each Monte-Carlo simulation, a maximum-flow optimization problem with a user defined priority of supply pattern is solved.
In order to model consequences during potential gas crises, a user given priority supply pattern is assumed for probabilistic reliability modelling of gas networks. Usually, the algorithm uses a priority supply pattern based on distances from source nodes: nodes geographically closer to the gas source are served first. This supply pattern was observed in gas transmission networks during previous European gas crises [3].
Let us describe the ProGasNet algorithm. In each Monte-Carlo simulation step, firstly component failures, it means failures of key gas network components (pipelines, LNG terminals and compressor stations), are sampled according to a given probabilistic law [6]. Then, an optimal maximum flow response of the gas network to the user-defined attack scenarios is evaluated and stored in a multidimensional flow matrix. For flow modelling, we use a maximum flow algorithm with multiple sources and sinks [7]. Moreover, a user defined priority of supply pattern is applied. Finally, the stored flow matrix is statistically analysed.
Of course, the flow model can be easily tuned if a prior flow information is available. For example, the maximum pipeline capacity at the cross-border connection point together with pipeline diameters can be taken from a transmission system operator (TSO) reports. A pipeline failure probability is modelled according to the EGIG report [14].
During gas supply crises, there is a necessary to maximize usage of gas sources and transmission elements under the given gas supply. Fortunately, the used maximum flow algorithm solves an optimization task, which guaranties an optimal solution, a maximum flow.
2.2 Component Importance Modelling in ProGasNet
According to [10], a risk importance measure gives an indication of the contribution of a certain component to the total risk. In this paper, we use two measures for calculation of the component importance: average gas deficit (AGD) and Risk Achievement (RA).


In our implementation, Risk Achievement is estimated as the non-delivery probability on the assumed attack scenario minus the non-delivery probability of the base-scenario (a “business as usual” scenario). In this study, we present results of probabilities that the gas delivery at selected demand node will be less than 80% of demands, i.e. RA < 0.8D. Results are discussed in Sect. 4.
When the both non-delivered probabilities are the same on the selected network node, the corresponding risk achievement is zero. It means that there is no security of supply impact of the selected attack scenario on the network node and the given risk level. Thus, the attack scenario is not important for the selected node and the risk level.
Average gas deficit is fast in identifying of dangerous attack scenarios. Then, Risk Achievement is used for more detailed analyses on the given risk level.
3 Definition of the Gas Network
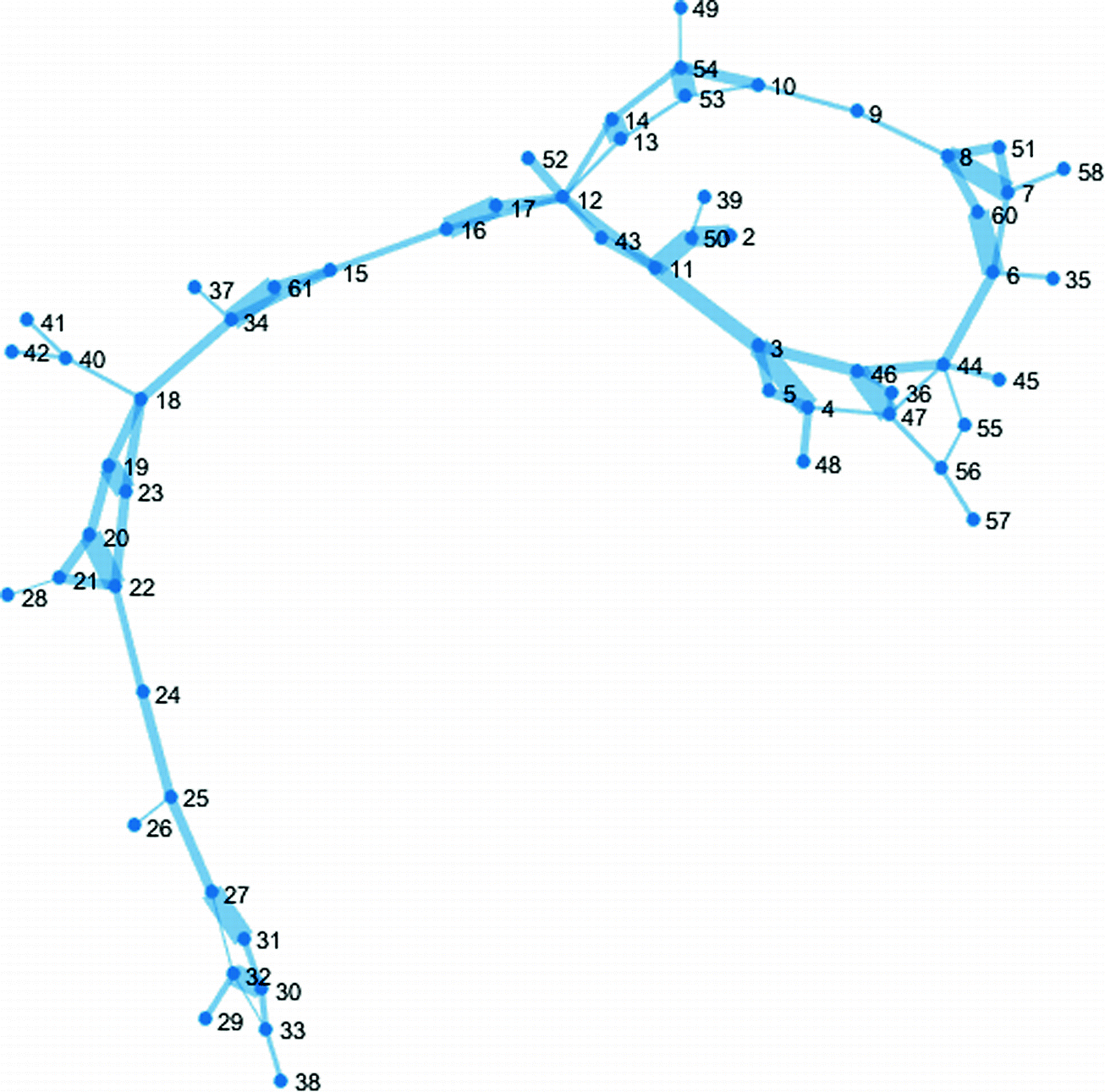
Anonymized topology of the analyzed European gas network. The linewidth is proportional to the pipeline capacity.
List of gas sources.
Node | Limit for Model P (mcm/d) | Yearly failure frequency for Model P | Limit for Model F (mcm/d) | Yearly failure frequency for Model F |
|---|---|---|---|---|
2 | 31 | 0 | 31.2 | 0 |
10 | 10.5 | 0.15 | 10.2 | f(C = 0) = 0.083; f(C = 5) = 0.125 |
19 | 25 | 0.1 | 26 | f(C = 0) = 0.046; f(C = 15) = 0.0625 |
29 | 4 | 0 | 4.3 | 0 |
38 | 0 | 0 | 2.3 | 0 |
59 | 0 | 0 | 7.1 | 0 |
62 | 0 | 0 | 7 | 0 |
Total | 70.5 | 88.1 |
List of non-zero demand nodes. The gas demand is represented by mcm/d. Node 64 represents the total demand in the network (Total).
Node | D(P) (mcm/d) | D(F) (mcm/d) | Diff (mcm/d) | Node | D(P) (mcm/d) | D(F) (mcm/d) | Diff (mcm/d) |
|---|---|---|---|---|---|---|---|
4 | 0.1 | 0.1 | 0 | 36 | 4.2 | 4.2 | 0 |
5 | 3.2 | 3.2 | 0 | 37 | 1.3 | 0.5 | 0.8 |
6 | 0.1 | 0.1 | 0 | 39 | 0.3 | 0.3 | 0 |
8 | 0.1 | 0.1 | 0 | 40 | 0 | 0.5 | −0.5 |
9 | 0.1 | 0.1 | 0 | 41 | 0.6 | 0.8 | −0.2 |
10 | 1 | 1 | 0 | 42 | 0.6 | 0.2 | 0.4 |
13 | 0.5 | 0.5 | 0 | 43 | 0.2 | 0.2 | 0 |
17 | 0.1 | 0.1 | 0 | 44 | 0.7 | 0.7 | 0 |
18 | 8.5 | 7.8 | 0.7 | 45 | 1.3 | 1.3 | 0 |
20 | 0.6 | 0.8 | −0.2 | 47 | 0.1 | 0.1 | 0 |
25 | 0.5 | 0.1 | 0.4 | 48 | 1.8 | 1.8 | 0 |
26 | 0.8 | 0.1 | 0.7 | 49 | 0.2 | 0.2 | 0 |
27 | 3 | 3.4 | −0.4 | 51 | 7 | 8.4 | −1.4 |
28 | 6 | 0 | 6 | 52 | 0.6 | 0.6 | 0 |
30 | 0.5 | 0.8 | −0.3 | 53 | 0.1 | 0.1 | 0 |
33 | 0.5 | 0.7 | −0.2 | 55 | 0.2 | 0.2 | 0 |
34 | 0.5 | 2 | −1.5 | 57 | 0.2 | 0.2 | 0 |
35 | 0.1 | 0.1 | 0 | 58 | 0.3 | 0.3 | 0 |
64 | 45.9 | 41.6 | 4.3 |
A comparison between Model P and Model F: List of improved pipeline sections with a positive capacity increase in mcm/d and the length of new pipelines in km.
From node | To node | Capacity (mcm/d) | Length (km) |
|---|---|---|---|
4 | 11 | 12.11 | 29 |
4 | 56 | 12.11 | 59 |
15 | 16 | 6 | 0 |
18 | 61 | 12.11 | 43 |
22 | 24 | 3 | 0 |
31 | 59 | 12.11 | 50 |
44 | 60 | 12.11 | 11.6 |
56 | 62 | 12.11 | 65 |
Table 3 presents a comparison between Model P and Model F, respectively. The table includes list of improved pipeline sections with a positive capacity increase in mcm/d and the length of new pipelines in km. If length of a new pipeline is zero, it means that no new pipeline has been added: The reported capacity increase is due to an enhancement of the network in this case. For example, the pipeline connecting node 15 with node 16 is not new (i.e. represented by 0 km pipeline length). On the other hand, the pipeline capacity has been increased by 6 mcm/d: as a result of the new gas infrastructure project.
The network encloses various gas network elements: pipelines, LNG terminal (node 10), gas storage (node 19) and compressor stations (nodes 11, 12). Properties of gas sources are presented at Table 1. All numbers have million of cubic meter per day dimension. Let us remind that probabilistic modelling of new infrastructure projects, especially a reliability quantification of redundancy of gas supply, was studied in [3].
According to literature indications [3], we set for Model P the monthly failure frequency of the LNG terminal to fLNG = 0.15/12 = 1.25E−2 and the monthly failure frequency of the gas storage (node 19) to fstorage = 0.1/12 = 8.33E−3, respectively. In contrary to Model P, we use a more detailed multi-state representation of these two gas sources for Model F, see Table 1. Here symbol C denotes the gas source limit expressed by mcm/d. For example, C = 0 means that the gas source is disconnected. The remaining gas sources are modelled as statistically reliable sources.
Finally, Table 2 shows a list of demand nodes for Model P and for Model F represented by the column D(P) and D(F), respectively. All demand numbers are expressed by mcm/d, too. A difference between these demands is summarized in the column ‘Diff’, which is also expressed by mcm/d. We can see that the largest positive difference is for node 28: 6 mcm/d, whereas the largest negative difference is for node 51: −1.4 mcm/d. Let us remind that probabilistic modelling of new infrastructure projects with constant demand was studied in [3–6].
The gas network elements can fail according to a given probabilistic model. For example, a pipeline failure is modelled by the reduction of the pipeline capacity to zero. According to the EGIG report [14], the average failure frequency of a European gas transmission pipeline is 3.5E−4 per kilometer-year. Let us assume that 10% of the reported failures cause complete rupture of a pipeline. The assumed 10% represents the pipeline rupture, according to the EGIG report. As a result, we set the pipeline failure frequency as 3.5E−5 per kilometer-year [3]. The model uses annual failure data (probability of failure per year), however when simulations are performed, one month interval is considered.
List of attack scenarios.
Scen. | From | To | From | To |
|---|---|---|---|---|
S1 | 29 | 32 | ||
S2 | 27 | 32 | 30 | 31 |
S3 | 25 | 27 | ||
S4 | 24 | 25 | ||
S5 | 22 | 24 | ||
S6 | 20 | 21 | 21 | 22 |
S7 | 21 | 28 | ||
S8 | 19 | 20 | 22 | 23 |
S9 | 18 | 19 | 18 | 23 |
S10 | 18 | 34 | 18 | 61 |
S11 | 15 | 34 | 15 | 61 |
S12 | 12 | 17 | 12 | 16 |
S13 | 12 | 13 | 12 | 14 |
S14 | 13 | 53 | 14 | 54 |
S15 | 10 | 53 | 10 | 54 |
S16 | 9 | 10 | ||
S17 | 8 | 9 | ||
S18 | 7 | 51 | 8 | 51 |
S19 | 6 | 7 | 8 | 60 |
S20 | 6 | 44 | 44 | 60 |
S21 | 44 | 46 | 44 | 47 |
S22 | 36 | 46 | 36 | 47 |
S23 | 3 | 46 | 4 | 47 |
S24 | 3 | 5 | 4 | 5 |
S25 | 3 | 11 | 4 | 11 |
S26 | 11 | 50 | ||
S27 | 2 | 50 | ||
S28 | 11 | 12 | 12 | 43 |
S29 | 11 | 43 | 12 | 43 |
S30 | 1 | 19 | ||
S31 | 1 | 10 |
In the next section, we will evaluate, how important is each segment of the back-bone for security of gas supply. We will evaluate security of supply consequences of these selected attack scenarios by the Monte-Carlo method.
4 Results of Simulations
In this section, we will describe results of 1 million of Monte-Carlo simulations applied to 31 attack scenarios of the transmission gas network back-bone. In order to highlight the most important reliability aspects, we will analyse the overall security of supply situation in the network and also security of supply situation on the selected 7 demand nodes.
Sorted results for Model P: Selected attack scenarios vs. average gas deficit and estimated risk achievement that the gas delivery at selected demand nodes will be less than 80% of demands. Negative values indicate a positive energy supply impact, and vice versa.
Importance(P) | Scen/Node | AGD (mcm/d) | RA < 0.8D | ||||
|---|---|---|---|---|---|---|---|
Total | Reg1 | Reg2 | Reg3 | Reg4 | |||
45.9 | 15.5 | 12.1 | 5.3 | 7 | |||
1 | S25 | 16.79 | 9.9E−01 | 1 | 0 | 0 | 1 |
2 | S30 | 13.41 | 9.9E−01 | 1.5E−04 | 9.9E−01 | 9.9E−01 | 2.8E−04 |
3 | S23 | 11.69 | 9.9E−01 | 1 | 0 | 0 | 1 |
4 | S8 | 7.95 | 1.4E−03 | 0 | 1.0E−06 | 9.9E−01 | 0 |
5 | S18 | 7.12 | 6.9E−05 | 0 | 0 | 0 | 1 |
6 | S27 | 6.75 | 1.4E−02 | 2.3E−02 | 0 | 0 | 1 |
7 | S26 | 6.45 | 1.4E−02 | 2.2E−02 | 0 | 0 | 1 |
8 | S6 | 6.07 | 2.5E−04 | 0 | 0 | 0 | 0 |
9 | S7 | 6.07 | 2.5E−04 | 0 | 0 | 0 | 0 |
10 | S21 | 5.85 | 1.0E−06 | 0 | 0 | 0 | 1 |
11 | S9 | 5.57 | 4.6E−04 | 1.5E−04 | 9.9E−01 | 0 | 2.8E−04 |
12 | S20 | 4.99 | 1.0E−06 | 6.4E−05 | 0 | 0 | 1 |
13 | S19 | 4.79 | 1.0E−06 | 6.4E−05 | 0 | 0 | 1 |
14 | S22 | 4.32 | 1.0E−06 | 1 | 0 | 0 | −1.0E−06 |
15 | S24 | 3.32 | 0 | 1 | 0 | 0 | −1.0E−06 |
16 | S4 | 1.41 | 0 | 0 | 0 | 9.9E−01 | 0 |
17 | S5 | 1.41 | 0 | 0 | 0 | 9.9E−01 | 0 |
18 | S29 | 0.32 | 0 | 0 | 0 | 0 | 0 |
- 1.
Scenarios S25, S30 and S23 with average gas deficit larger than 10 mcm/d and with RA < 0.8D for demand node Total ~1
- 2.
Scenarios S8 and S18 with average gas deficit between 7 and 8 mcm/d
- 3.
Scenarios S26, S27 with average gas deficit close to 6.5 mcm/d and with RA < 0.8D for demand node Total ~0.014, which corresponds to a failure rate of gas source at node 10
- 4.
The remaining scenarios with average gas deficit 6.07 mcm/d or less
The largest security of supply consequences has Scenario S25, which represents a failure of node 3 to node 11 pipeline and a failure of node 4 to node 11 pipeline (only for Model F). However, only demand nodes Region1 and Region4 are highly affected, as their RA scores are close to 1. The second largest consequence has Scenario S30, i.e. disruption of source node 19 (a second largest gas source in the network). We can also see that only demand nodes Region2 and Region3 are highly affected. On the other hand, the security of supply situation at Region1 and Region4 is almost not affected: RA scores are close to zero (E-04 order).
Attack scenarios S26 and S27 represent cases in which the largest gas source (node 2) is partially or fully lost. Risk achievement for demand node Total for these cases is around 1.4E−2. This value is related mainly to the failure frequency of gas source at node 10. Thus, a failure of the largest gas source can be compensated in these two attack scenarios by the gas source at node 10. However, the gas deficit mainly affects Region4, which demands 7 mcm/d.
Let us analyse a situation at selected regions. Region4 represents the most vulnerable part of the network: 8 of top 18 attack scenarios have RA ~1, namely S18-S21, S23, S25−S27. Fortunately, the rest of scenarios lead to risk achievement scores, which are close to zero. In contrary to Region4, Region1 and Region3 are much less vulnerable to analysed attacks: 4 of 15 scenarios have RA ~1. In contrary to Region3, Region1 is partially sensitive to above mentioned S26 and S27 attacks. However, these two attacks lead to a relative small risk achievement for Region1: around 2.2E−2. Finally, Region2 is quite resilient to attacks, as only 2 scenarios have RA scores close to 1: S9 and S30. Consequently, importance of the second largest gas source (node 19) is evident for Region2.
Table 5 include also ‘paradoxes’: negative RA values for Region4. These values indicate a fact, that Region4 can profit, when an attack scenario occurs. However, these situations occur very rarely, as negative risk achievement values are very close to zero (order of 1E−6).
Sorted results for Model F: Selected attack scenarios vs. average gas deficit and estimated risk achievement that the gas delivery at selected demand nodes will be less than 80% of demands. Negative values indicate a positive energy supply impact, and vice versa.
Importance(F) | Scen/Node | AGD (mcm/d) | RA < 0.8D | ||||
|---|---|---|---|---|---|---|---|
Total | Reg1 | Reg2 | Reg3 | Reg4 | |||
41.6 | 15.5 | 12.6 | 5.1 | 8.4 | |||
1 | S25 | 11.07 | 1 | 8.3E−04 | 0 | 0 | 1 |
2 | S23 | 9.74 | 1 | 6.1E−04 | 0 | 0 | 1 |
3 | S18 | 8.40 | 1 | 0 | 0 | 0 | 1 |
4 | S21 | 7.13 | 1.2E−03 | 1.6E−05 | 0 | 0 | 1 |
5 | S20 | 6.27 | 5.1E−04 | 1.6E−05 | 0 | 0 | 1 |
6 | S19 | 6.07 | 4.5E−04 | 1.6E−05 | 0 | 0 | 1 |
7 | S22 | 4.20 | 5.6E−05 | 1 | 0 | 0 | −3.0E−05 |
8 | S24 | 3.20 | 1.0E−04 | 1 | 0 | 0 | −1.9E−05 |
9 | S29 | 0.20 | 0 | 0 | 0 | 0 | 4.8E−05 |
10 | S27 | 0.08 | 3.8E−03 | 8.1E−05 | 8.2E−05 | 0 | 1.1E−02 |
11 | S9 | 0.08 | 4.2E−03 | 7.7E−05 | 4.3E−03 | 0 | 4.1E−03 |
12 | S26 | 0.08 | 3.8E−03 | 7.8E−05 | 8.2E−05 | 0 | 1.1E−02 |
13 | S28 | 0.05 | 4.2E−03 | 1.7E−03 | 3.7E−05 | 0 | 4.1E−03 |
14 | S30 | 0.05 | 4.2E−03 | 7.7E−05 | 9.3E−05 | 0 | 4.1E−03 |
15 | S10 | 0.05 | 4.2E−03 | 7.6E−05 | 1.2E−05 | 0 | 4.1E−03 |
Let us compare number of scenarios with average gas deficit larger than 1 mcm/d. Model P includes 17 scenarios, whereas Model F includes only 8 scenarios. Let us analyse these most critical attack scenarios.
A comparison of top 18 attack scenarios of Model P with Model F results by the average gas deficit.
ImportanceP | Scen | AGD(P) (mcm/d) | ImportanceF | AGD(F) (mcm/d) | Deficit reduction (mcm/d) | Relative deficit reduction (%) |
|---|---|---|---|---|---|---|
1 | S25 | 16.79 | 1 | 11.07 | 5.72 | 34 |
2 | S30 | 13.41 | 14 | 0.05 | 13.36 | 99.6 |
3 | S23 | 11.69 | 2 | 9.74 | 1.95 | 16.7 |
4 | S8 | 7.95 | 26 | 0 | 7.95 | 99.9 |
5 | S18 | 7.12 | 3 | 8.4 | −1.28 | −18 |
6 | S27 | 6.75 | 10 | 0.08 | 6.67 | 98.8 |
7 | S26 | 6.45 | 12 | 0.08 | 6.37 | 98.8 |
8 | S6 | 6.07 | 30 | 0 | 6.07 | 99.9 |
9 | S7 | 6.07 | 31 | 0 | 6.07 | 99.9 |
10 | S21 | 5.85 | 4 | 7.13 | −1.28 | −21.9 |
11 | S9 | 5.57 | 11 | 0.08 | 5.49 | 98.5 |
12 | S20 | 4.99 | 5 | 6.27 | −1.28 | −25.7 |
13 | S19 | 4.79 | 6 | 6.07 | −1.28 | −26.8 |
14 | S22 | 4.32 | 7 | 4.2 | 0.12 | 2.7 |
15 | S24 | 3.32 | 8 | 3.2 | 0.12 | 3.6 |
16 | S4 | 1.41 | 24 | 0.01 | 1.4 | 99.3 |
17 | S5 | 1.41 | 25 | 0.01 | 1.4 | 99.3 |
18 | S29 | 0.32 | 9 | 0.2 | 0.12 | 37.5 |
The second most critical scenario for Model P was S30. However, this scenario is ranked on 14-th place for Model F, as the average gas deficit is very close to zero for Model F: only 0.05 mcm/d. Thus, the average gas deficit has been reduced by 13.36 mcm/d, i.e. by 99.6%, see Table 7. This result clearly indicates positive security of supply effects of the new infrastructure project.
Scenario S23 remains on the top 3 critical list, but the average deficit has been reduced from 11.69 mcm/d to 9.74 mcm/d, i.e. by 16.7%, see Table 7.
On the other hand, Table 6 includes 4 scenarios, in which the average gas deficit has been increased: see results of scenarios S18–S21. The lines corresponding to these scenarios are highlighted in bold, see Tables 6 and 7. The reason why the average gas deficit has been increased is simple: Demand of Region4 has been increased from 7 mcm/d (Model P) to 8.4 mcm/d in Model F. We can see from Table 6 that risk achievement of Region4 for attacks S18–S21 is equal to 1 also in Model F.
Although the total limit of gas sources has been increased from 70.5 mcm/d to 88.1 mcm/d (see Table 1) and the total network demand has been reduced from 45.9 mcm/d to 41.6 mcm/d (Table 2), Model F is not fully able to respond to the increased demand of Region4. The reason is that Region4 represents a geographically remoted consumer, in which the transmission network capacity is limited by a bottleneck. In the other words, although there are gas sources available, there is not enough transmission capacity to pump gas to Region4, even a new infrastructure project has been implemented.
In contrary to Model P, Model F reduced the average gas deficit almost to zero in 9 attack scenarios: S4–S9, S26, S27 and S30. Let us remind that S30 was the scenario with the second largest average gas deficit in Model P: 13.41 mcm/d.
Finally, there are 5 scenarios, in which the average gas deficit has been partially reduced: S22–S25 and S29. In these scenarios, the average deficit reduction is between 0.12 mcm/d (for S22, S24 and S29) and 5.72 mcm/d (for S25).
5 Conclusions
We presented a probabilistic approach for identification and ranking of important gas network elements. We used a combination of two measures for calculation of the component importance: average gas deficit and Risk Achievement. In order to evaluate security of supply consequences of a new gas infrastructure project, this analysis was performed twice: before and after the infrastructure project.
The results of 31 selected attack scenarios under 1 million of Monte Carlo steps were automatically analysed and compared in ProGasNet, in order to obtain information, how the gas network can optimally react under various constrains (random component failures) and under the given attack scenarios. Results indicate that the new infrastructure project was very helpful for the analysed gas network, as the number of attack scenarios with a large gas deficit (1 mcm/d or more) has been reduced from 17 to 8. However, we identified 4 scenarios, in which the average gas deficit is larger than before. Even when a new infrastructure project has been implemented, the network is not able to transfer enough gas to Region4, because of a network bottleneck, as demand of Region4 increased.
On the other hand, majority of failure consequences of the largest gas source can be reliably compensated by the third largest gas source. Moreover, simulated results clearly show that the gas network is not critically sensitive to disruptions leading to disconnection (or a failure) of the second largest gas source, when the new gas infrastructure is implemented.
The ProGasNet approach for identification and ranking of important gas network elements by a combination of two measures for calculation of the component importance was very useful for large number of attack scenarios.