© Springer Nature Switzerland AG 2019
Eric Luiijf, Inga Žutautaitė and Bernhard M. Hämmerli (eds.)Critical Information Infrastructures SecurityLecture Notes in Computer Science11260https://doi.org/10.1007/978-3-030-05849-4_2

In-Cycle Sequential Topology Faults and Attacks: Effects on State Estimation

Ammara Gul1   and Stephen Wolthusen1, 2  
(1)
Information Security Group, Royal Holloway University of London, Egham, Surrey, TW20 0EX, UK
(2)
Norwegian Information Security Laboratory, Gjovik University College, Gjovik, Norway
 
 
Ammara Gul (Corresponding author)
Email: ammara.gul.2015@live.rhul.ac.uk
 
Stephen Wolthusen
Email: stephen.wolthusen@rhul.ac.uk

Abstract

Monitoring and state estimation as well as ultimately higher-order tasks in power networks require timely and accurate measurements arising from a wide area network. Knowledge of the current topology of the network is crucial to interpret any such measurements and is also required for state estimators to obtain correct results. As both faults and deliberate actions such as opening breakers may alter the topology, an important step in any state estimator is topology processing to obtain an accurate view for a given set of measurements. This, however, is conventionally performed prior to state estimation. We argue that this gives adversaries an opportunity to stealthily induce and possibly revert topology changes within a single scan cycle, resulting in some results being influenced by the intermittent changes as conventional models rely on the abstraction that all measurements to arrive instantly and synchronously. We provide a formal model of the attack and formulate an optimisation problem to minimise the cost to attackers and determine the effects of induced topology faults, resulting in denial of service attacks up to loss of observability and study recoverability. Finally, we compare our approach to conventional contingency analysis and offer simulation results based on the standard IEEE-14 and IEEE-30 test cases.

Keywords

Power systemSmart gridState estimationSequential topology changeScan cycleTopology processing

1 Introduction

Monitoring and state estimation require accurate knowledge of the underlying topology of the power network to take effective control actions in addition to raw measurements. A substantial body of work exists on vulnerabilities of such systems to malicious false data injection, but this tends to assume that the underlying power network topology is known and static for the duration of both operation and attack; the conventional approach for state estimation being to perform topology processing [1] prior to state estimation.

However, modern power networks are likely to be more dynamic as particularly generators based on renewable energy may have intermittent availability and can also be configured in the form of virtual power stations; this renders contingency case analysis more problematic already even in the absence of active attackers. In this paper we concentrate on studying the effects of topology faults, particularly when introduced deliberately.

Information on how generators and loads are connected via buses, transformers, tie and transmission lines are obtained from equipment state information in the form of binary state or that can be further corroborated by other analogue measurements (phase, voltage, current), and are commonly subjected to topology processing, which seeks to eliminate errors based on wrongly recorded equipment state as well as the presence of faults.

Topology changes may include tripping of generators, accidental line failures, or deliberate attacks; the former is commonly handled based on contingency analyses, but combinatorial limits prevent this from extending beyond single line failures.

Topology processors identify the network, connectivity, and location of measurement devices. Conventional topology processing is performed before state estimation and functions such as observability analysis and bad data processing take place. Once the network topology is known, state estimation assumes that this topology is correct and proceeds to estimate the state and identify analogue bad data. Generalized topology processing extends this with explicit modelling of switches, but is not widely deployed [1].

The research reported in this paper is motivated by the relative paucity of work on topology-related attacks compared to the body of research on bad data injection and related data-based attacks. Earlier work has studied single and double topology modifications, including induced double line faults and analyse the effects on state estimators in terms of possible state forcing or also state estimator divergence [2]. On the other hand, here we formulate a mechanism for finding optimal conditions for resource-constrained attacker and compare the results with conventional contingency cases while explicitly including the non-simultaneous capture of measurements, abandoning the abstraction of atomic measurements across the entire power system.

The main contribution of the present paper is therefore an analysis of the effects of transient faults and attacks, and we explicitly analyse a topology change taking place during a scan cycle. This way, the state of the topology remain unchanged in the beginning and the end of the measurement taking process therefore, making the attack sufficiently undetectable. We derive a metric to analyse the attack impact on state estimation motivated by the fact that there are some lines which have negligible effect on state estimation upon inclusion/removal, and on the other hand the possible existence of a small number of few other branches and lines whose addition/withdrawal may result in a catastrophic attack.

The remainder of this paper is structured as follows: Background and related work are briefly described in Sect. 2 followed by a description of the system models used in state estimation, bad-data detection, and identification in Sect. 3. Our novel topology attack model is presented in Sect. 4, along with the necessary conditions to make the attack feasible. In Sect. 5, simulation results are shown for the introduced attack on IEEE bus systems and feasibility of our proposed attack is also discussed. We provide conclusions as well as ongoing work in Sect. 6.

2 Related Work

Bad data injection attacks and their detection/mitigation is a widely researched area in power system state estimation, with a large body of work emerging since study of bad data injection was proposed in work by Liu et al. in [3]. However, substantially less attention has been paid to the other main cause of the faults namely topology errors.

Hines et al. [4] elaborated topological and electrical structure of the power grid while proposing a graph theoretic method for generating random networks similar to the power grid to better notice topology changes. Monitoring of power system topology in real-time is achieved currently by observing the circuit breaker’s (CB) operation and statuses by using Remote Transmission Units (RTUs) of a SCADA system. However, changes such as trip conditions, etc. cannot be determined solely by this SCADA approach. Kezunovic proposed a solution based on a new CB Monitor (CBM) which would be permanently connected to the substation CBs [5]. This CBM scheme can be extended to the system level, but deployment cost cannot be ignored.

In [6], Lu et al. proposed a rule-based topology error/change detection method in which all analogue data are screened before applying the heuristic rules to detect the errors. Although the results are appealing but, it is computationally expensive approach. Lefebrve et al. [7] proposed a pre-processing method for detecting and identifying topology errors and bad measurements before a state estimation solution. This incurs the drawback that every time a change in topology occurs, the system has to go through this whole process. Another different, yet complicated approach, is to take the status of switching devices as new state variables estimated together with usual ones while considering three state variables for one switch status [8].

Steady state simulations of power system with changes in topology are shown in [9] by collecting all the possible topologies as a result of isolation of transmission lines from the system. In principle detection and identification of topology changes in power systems by using PMUs is becoming more attractive as PMUs are more widely deployed. Placing PMUs at strategic points can help quickly detecting topology changes caused by events such as lines going down or large voltage drops [10]. A quick change algorithm is proposed to be applied on the data provided by high-speed PMUs to detect the change-point that corresponds to the system topology change instant [11]. A systematic bus selection scheme is presented for the minimum required PMUs. Taking into account the load dynamics and measurement error, the topology detection algorithm is constructed based on data from micro-synchrophasors or $$\mu $$PMUs [12]. [13] proposed that the minimal difference between measured and calculated voltage angle or magnitude indicates the actual topology and hence a method based on multiple $$\mu $$PMUs is devised.

Topology changes can be caused deliberately by the adversary to harm the power network. The attack as a result of topology change is known as hidden topology attack, where the attacker may need to change the status of just one circuit breaker at a transmission line and suppress the corresponding alert or measurements to make it hidden [14]. Frequent topology changes in today’s power system have raised a big challenge of assessing the system protection and security afterwards [15]. Further, an impact analysis of the topology change on relay settings is conducted.

A joint cyber and physical attack is analysed where the adversary attacks a zone by physically disconnecting some of the power lines and then blocking the information flow from the attacked zone to the control center [16]. Information recovery model following such attack is proposed to retrieve the data about the disconnected lines. The vulnerability of grid to such attacks is analysed and an efficient EXPOSE algorithm to detect and recover missing information is proposed [17]. Furthermore, the properties of the cascade and introduce algorithms to identify the cascading failure evolution and vulnerable lines in a linearized power-flow model are studied [18]. Classes of attacks including single and double topology modifications are studied and the effects on state estimators including possible state forcing or also state estimator divergence are analysed [2].

Lourenco et al. in [19] presents a method for processing real-time data error in generalized state estimation while considering both type of errors namely topology and analogue data errors. [20] reviews the most relevant works that have investigated robustness in power grids using Complex Networks (CN) concepts. Undetectable attacks on network topology of a smart grid are considered with a strong assumption that the adversary can observe all the meter and network data for existence of an undetectable attack [21].

Woodward in his report last year [22] quoted a research that 10.8% of all links in the US and Southern Canada are at risk of cascade event. Results imply that the same disturbance in a given power grid can lead to disparate outcomes under different conditions–ranging from no damage to a large-scale cascade is proposed by Wang et al. in [23]. It indicates that the topological and geographical properties of the vulnerable set is a major factor determining whether the failures spread widely. Xiao and Yeh study the problem of cascading link failures in power grids and model these failures by graph theoretic approach [24] while considering the fact that links fail according to a probability which depends on the neighbouring links.

3 Power System State Estimation and Topology Identification

Currently in our power grids, the control center receives two kinds of data from the metering devices throughout the system. Binary data $$\mathbf {s} \in \{0,1\}^{d}$$ corresponds to the switch status and circuit breakers knowledge and can be represented as a string of binary numbers denoting the on/off states of the switches/breakers. Analogue numbers are taken for real and reactive flows, injections, voltage and current measurements and we denote it by the measurement vector $$\mathbf {z}$$. When there is no attack or sensor error, $$\mathbf {s}$$ corresponds to a true switch/breaker states. Each $$\mathbf {s}$$ provides a network topology and we denote that topology by a directed graph $$\mathcal {G}= (\mathcal {V},\mathcal {E})$$ with a set of $$\mathcal {V}$$ buses and $$\mathcal {E}$$ transmission lines. The state of the power network is $$\mathbf {x}$$ which is a vector of voltage magnitude and phasors on all the buses of the network. When there is no attack, the measurements collected by SCADA, $$\mathbf {z}$$, the system state $$\mathbf {x}$$ and the topology defined above $$\mathcal {G}$$ are related by the AC power flow model
$$\begin{aligned} \mathbf {z}=h(\mathbf {x}, \mathcal {G})+\mathbf {e} \end{aligned}$$
(1)
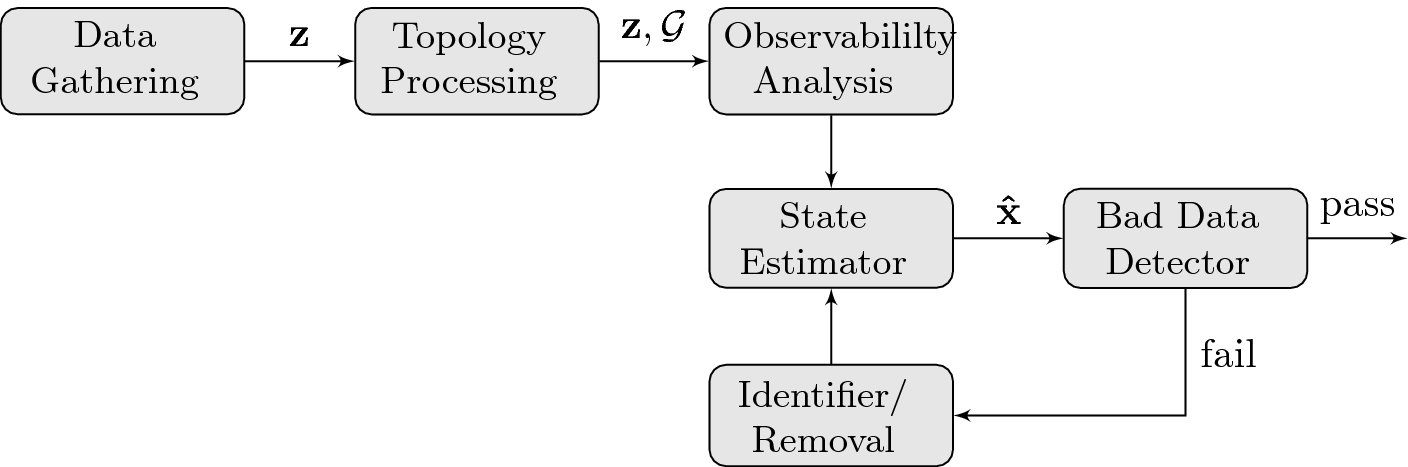
../images/477940_1_En_2_Chapter/477940_1_En_2_Fig1_HTML.png
Fig. 1.

Real-time modelling of a power network: conventional state estimation

where $$\mathbf {z}$$ is measurement vector consist of both real and reactive measurements, $$\mathbf {x}$$ is the state vector, h is the non-linear measurement function of $$\mathbf {x}$$ and $$\mathcal {G}$$ and $$\mathbf {e}$$ is the noise vector having zero mean and known co-variance $$\mathbf {R}$$ of order $$m\times n$$ where there are m measurements and n state variables $$(m>n)$$. As described by Monticelli, the control center executes state estimation with network information and meter readings as inputs [1]. Figure 1 represent this SE where network and meter data are $$(\mathbf {s},\mathbf {z})$$. It checks both the network information and the measurement data for errors. If the bad data test in SE detects some inconsistencies in the data and the estimates, it refines the data by removing the outliers and then searches for the topology and the estimates that matches the best with the data. Our aim of an undetectable topology attack is achieved when one may pass through bad data test without raising an alarm.

If $$(\mathbf {s},\mathbf {z})$$ is the input to state estimation under the AC model given by (1) and $$\mathbf {s}$$ corresponds the topology $$\hat{\mathcal {G}}$$, the control center acquire the Weighted Least Square (WLS) estimate by
$$\begin{aligned} \mathbf {\hat{x}}= \text {argmin} (\mathbf {z}-h(\mathbf {x},\mathcal {\hat{G}}))^{t}\mathbf {R}^{-1} (\mathbf {z}-h(\mathbf {x},\mathcal {\hat{G}})) \end{aligned}$$
(2)
where $$\hat{\mathcal {G}}$$ is network topology when there is no attack and $$\bar{\mathcal {G}}$$ when there is a topology attack. Although Weighted Least Absolute Value (WLAV) method for state estimation is more robust and stable in the sense that it is able to reject bad data efficiently but it has some major drawbacks i.e., it involves time consuming Linear Programming (LP) technique and slow convergence rate among others. Therefore, WLS, although not that effective in presence of bad data, is considered as the most widely used method to SE problems (see [25] for details).
Once the states $$\mathbf {\hat{x}}$$ are estimated, bad data analysis is done. Generally, control center uses residue error for bad data detection. In $$J(\mathbf {\hat{x}})$$, the WLS error
$$ J(\mathbf {\hat{x}})= (\mathbf {z}-h(\mathbf {\hat{x}},\hat{\mathcal {G}}))^{t}R^{-1} (\mathbf {z}-h(\mathbf {\hat{x}},\hat{\mathcal {G}})) $$
is used and a statistical threshold $$\tau $$ is used
$$\begin{aligned} {\left\{ \begin{array}{ll} \text {bad data} &{} \;\;\; \text {if} \;J(\mathbf {\hat{x}}) > \tau \\ \text {good data} &{} \;\;\; \text {if} \;J(\mathbf {\hat{x}})\le \tau \end{array}\right. } \end{aligned}$$
(3)
where $$\tau $$ is determined to meet $$\alpha $$ which is the condition of false alarm. We define the undetectable topology attack as the one with the detection probability as low as rate of false alarm.

4 Sequential Topology Failures

With a dynamic power grid that we have today, it is fair to expect frequent topology changes. The expertise of power engineers rely on the smooth and steady operation of the grid despite these recurrent changes in topology. Deployment of Phasor Measurement Units (PMUs) is allowing topology change detection schemes to be more accurate and significantly faster [7, 10]. Hundreds of PMUs are being deployed round the globe to increase the redundancy in measurement vector and help getting topology changes detected, therefore contributing to more secure power grid. The major issue related to this advancement is the cost of these advanced devices. Due to this constraint, there are still thousands of branches with no PMUs leaving room for the attackers. Even if it is possible to have PMUs at every line, there is still a potential chance for the attacker such as by aiming at GPS, a time reference signal upon which generally all PMUs rely. Spoofing of such signals is very common and inexpensive source to create confusion about the correct signals in the control centre.

To make a clear understanding about how the power grid responses towards such changes we need to report some preliminaries from previous works. An attack (error) that can pass through the system without being noticed by the bad data test is called an undetectable attack. Such attacks (errors) can be classified further as data-based or topology-based, both of which require some criterion to get the desired impact. Undetectable false data injection attacks on state estimation as introduced by Liu et al. [3] have a necessary condition of undetectability as: Suppose the original measurements $$\mathbf {z}$$ can pass the bad measurement detection. The malicious measurements $$\bar{\mathbf {z}} = \mathbf {z}+\mathbf {a}$$ can pass the bad measurement detection if $$\mathbf {a}$$ lies in a column space of H i.e., $$\mathbf {a} \in Col(H)$$. On the other hand, for a topology-related attack, Kim and Tong proposed a similar undetectability condition as Suppose the original measurement set $$(\mathbf {z}; \mathbf {s})$$ can pass the bad measurement detection. The malicious measurements $$\bar{\mathbf {z}} = \mathbf {z} + \mathbf {a}$$ can pass the bad measurement detection if $$\bar{\mathbf {z}}$$ lies in a column space of $$\bar{H}$$ where s denotes the topological data and $$\bar{H}$$ is the measurement matrix after topology attack $$\bar{\mathcal {G}}$$ [21].

Details of the undetectable single/multiple topology attack and the related possibilities for the attacker to create misconception among the operators can be found in [2]. Here, we are introducing a novel sequential topology attack that goes undetected due to its reverse nature. In addition, in both of our works i.e., the previous and the present one, we consider these faults as a result of deliberately induced error. However, such errors can also emerge due to some natural reasons for example thunderstorms, earthquakes, floods, or even high winds that are not under the scope of this paper.

4.1 Adversary Model

In this section, we intend to analyse the attack model for transient topology changes in a single scan cycle. There are usually two scenarios when SCADA systems transmit the measurement data collected from sensors i.e., (I) the devices will sent a message if something interesting/unusual happens and (II) SCADA systems need to complete its scan/poll cycle despite of some changes. Theoretically, former is correct as protocols allow one to perform it but such a synchronization is relatively uncommon. Contrarily, later is common traditionally which is a deterministic real-time behaviour where every deadline is maintained within a certain time period.

As an attacker, we are considering the most widely used behaviour of SCADA systems where SCADA take a definite amount of time after coming back to the same sensor. In fact some sensors are slightly slower or faster compared to others. In other words, there must be an interval between each time the measurements being integrated leaving a possibility for the attacker. As long as the attacker maintains operation(s) within that frame of single scan cycle while keeping itself hidden, the attack can be made successful.

The attacker aims to change the current topology $$\mathcal {G}$$ to a desired topology $$\mathcal {\bar{G}}=(\mathcal {V}; \mathcal {\bar{E}})$$ and then reverses that change before the completion of the scan cycle such that the final topology $$\mathcal {\bar{\bar{G}}}=(\mathcal {V}; \mathcal {\bar{\bar{E}}})$$ would be same as it was in the start i.e., $$\mathcal {\bar{\bar{G}}}=\mathcal {G}$$. This attack only involves line faults, therefore, the number of vertices $$\mathcal {V}$$ (bus-bars) will remain the same during the attack but the number of edges $$\mathcal {E}$$ (transmission lines) will become $$\mathcal {\bar{E}}$$ or $$\mathcal {\bar{\bar{E}}}$$ where $$\mathcal {E}\subset \mathcal {\bar{E}}$$, $$\mathcal {E}= \mathcal {\bar{\bar{E}}}$$. The lines that are not common between $$\mathcal {E}$$ and $$\mathcal {\bar{E}}$$ and between $$\mathcal {\bar{E}}$$ and $$\mathcal {\bar{\bar{E}}}$$ are called attacked lines in the first and second attack intervals respectively. Similarly, all the buses with which target/attacked lines are connected are called attacked buses (Fig. 2).
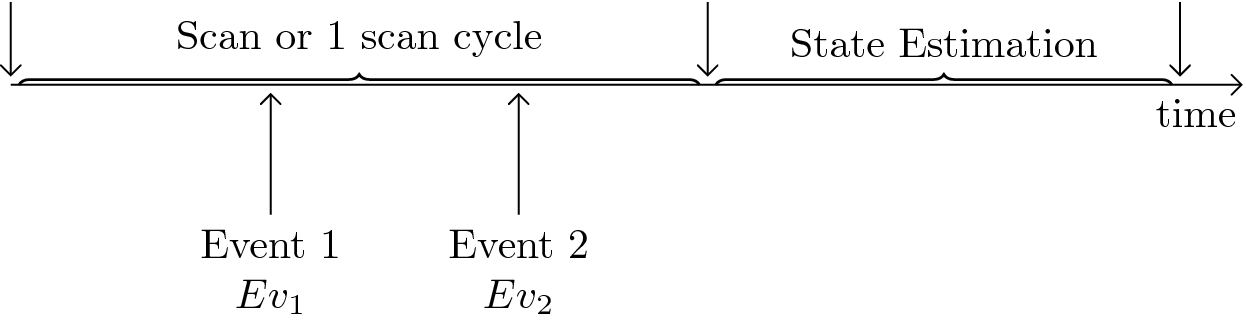
../images/477940_1_En_2_Chapter/477940_1_En_2_Fig2_HTML.png
Fig. 2.

Sequential topology attack model

As a prerequisite, the attacker must have the knowledge of few of the time windows in between two scan cycles where the success probability is maximum. In the beginning of a particular scan cycle, the attacker closes already open circuit breakers/switches. The corresponding measurements from the relative sensor changes themselves due to the change in topology. Before the end of the same cycle, the attacker switch the statuses back to its original (open) position such that the topology now $$\mathcal {\bar{\bar{E}}}$$ is same as was before the manipulation i.e., $$\mathcal {\bar{\bar{E}}}=\mathcal {E}$$. To launch such a sequential or a two-stage attack, the attacker at first, needs to change the status of a single breaker from $$0 \rightarrow 1$$ and then within the scan of measurements, the attacker needs to reverse that change i.e., $$1 \rightarrow 0$$.
$$\begin{aligned} \begin{aligned}&\mathbf {\bar{s}} = \mathbf {s} + \mathbf {a}, \;\;\;\; \mathbf {a} \in \{0,1\}\\&\mathbf {\bar{\bar{s}}} = \mathbf {\bar{s}} + \mathbf {b}, \;\;\;\; \mathbf {b} \in \{0,1\} \end{aligned} \end{aligned}$$
(4)
where $$\mathbf {a}$$ and $$\mathbf {b}$$ are the topology changes at first and second stage of the sequential attack respectively. The attacker is limited in resources in terms of time availability and therefore, the necessary but not sufficient condition for the attacker about time limitation will be
$$\begin{aligned} \mathbf {\bar{s}} - \mathbf {\bar{\bar{s}}} \le \mathbf {T}, \;\;\;\; \mathbf {\bar{s}} \in \mathcal {\bar{G}}, \mathbf {\bar{\bar{s}}} \in \bar{\bar{\mathcal {G}}} \end{aligned}$$
(5)
where $$\mathbf {\bar{\bar{s}}}-\mathbf {\bar{s}}$$ is the length of the attack. This constraint limit the attacker such that he must launch and complete the attack before the next scan cycle starts. There is no proper attack vector in both stages of this attack as the amount of topology change induced by the attacker is reversed inside the same scan cycle. It is important to mention that the above model can be seen as a more realistic extension of [3] where Liu et al. introduced a as an amount of change in the true measurement data. The difference here is of the resources available to the attacker along with very low detection probability and the similarity is the ultimate data fault caused by the attacker.
The measurement vector can be seen as a collection of measurements at three instants, (1) before attack, (2) after first attack and (3) after second sequential attack
$$\begin{aligned} \mathbf {z}^{*} = \begin{bmatrix} 1 \\ 1 \\ \vdots \\ 1\\ 0\\ 0\\ 0\\ \vdots \\ 0 \end{bmatrix}\cdot \mathbf {z}' + \begin{bmatrix} 0 \\ \vdots \\ 0 \\ 1\\ \vdots \\ 1\\ 0\\ \vdots \\ 0 \end{bmatrix}\cdot \mathbf {z}''+ \begin{bmatrix} 0 \\ 0\\ 0\\ \vdots \\ 0 \\ 1\\ 1\\ \vdots \\ 1 \end{bmatrix}\cdot \mathbf {z}''' \end{aligned}$$
(6)
where $$\mathbf {z}^{*}$$ is the manipulated measurement vector. After the attack, states can be determined by Eq. 2 as
$$\begin{aligned} \mathbf {\hat{x}^{*}}= \text {argmin} (\mathbf {z}_{A}^{*}-\hat{H}\mathbf {x})^{t}\mathbf {R}^{-1} (\mathbf {z}_{A}^{*}-\hat{H}\mathbf {x}) \end{aligned}$$
(7)
where $$\mathbf {\hat{x}^{*}}$$ is the false state vector.

The success of the attack lies on how bad is its influence on the measurements in between such sequential change and then how the compromised measurements impact the state estimation process. If the topology before the scan cycle would not match the topology after it, the operators could simply reject the corresponding data and go for contingency analysis. However, even if it not a sequential attack, the first attack alone can cause damage to the system but here, the adversary is aiming for its desired impact or at most DoS attack.

The least cost attack can be seen as the one with the most impact $$\mathcal {I}$$ on the operation of power grid such as
$$\begin{aligned}&\!\max \;\;\mathcal {I}\;\;=&\qquad&\parallel \bar{\mathbf {z}}-\bar{\bar{\mathbf {z}}}\parallel _{0}\end{aligned}$$
(8a)
$$\begin{aligned}&\text {subject to}&\parallel \bar{\mathbf {z}}-\bar{\bar{\mathbf {z}}}\parallel _{1} \le \alpha ,\end{aligned}$$
(8b)
$$\begin{aligned}&&z_{km} = \infty \;\text {if} \; \mathbf {\bar{s}}: 1 \rightarrow 0 . \end{aligned}$$
(8c)
where $$\bar{\mathbf {z}}$$ and $$\bar{\bar{\mathbf {z}}}$$ are the manipulated and true measurements respectively. $$\parallel \cdot \parallel _{0}$$ is the total number of non-zero entries in a vector and $$\parallel \cdot \parallel _{1}$$ is the magnitude. Equation 8 is a an optimization problem with an objective function maximizing the impact of the proposed topology attack by finding the optimum for the number of modifications required. The impact $$\mathcal {I}$$ depends on the total number of measurements between the two stages of the attack i.e., $$\mathbf {\bar{s}}$$ and $$\mathbf {\bar{\bar{s}}}$$. Constraint 8b denotes that the magnitude of change is bounded while Eq. 8c shows the stealth condition. $$z_{kl}$$ is the line impedance for kl where k and l denote the end buses.

5 Results and Discussions

We note that we seek to consider undetectable topology attacks on conventional centralised state estimation. In this section, we discuss the performance of the above mentioned state estimation model as a result of sequential topology errors by simulations on IEEE 14 and 30-bus systems. The technique used to estimate the state is WLS and MATPOWER is used for loading the data for AC model. Note that, without any topology attack both systems take 4 iterations to converge.

Our sequential attack is composed of two stages to be completed in a single scan cycle. It is worth mentioning here that we consider the same transmission line in both stages i.e., first stage of attack is opening a line while the second stage is closing the same line. Table 1 shows that there is always an impact no matter which line is under attack. After N simulations for each bus system, where N is the total number of lines in a system we notice that our attack model remain successful whether it is about the error in estimated states or delayed convergence.
Table 1.

Sequential faults in 14 and 30-bus system

Test case

Failed line

Convergence (iterations)

Error (MSE)

Single LF

Sequential LF

Single LF

Sequential LF

14-bus system

1–2

4 iterations

4 iterations

83.19

3.455

2–3

4 iterations

5 iterations

0.0003

0.6424

5–8

4 iterations

7 iterations

0.0013

0.4731

3–14

4 iterations

5 iterations

0.0001

0.287

30-bus system

1–2

4 iterations

5 iterations

0.0001

6.159

2–4

diverge

6 iterations

$$\infty $$

108.12

4–12

4 iterations

4 iterations

0.0001

6.53

24–25

diverge

6 iterations

$$\infty $$

6.16

In above table, the first and second columns are for the considered test systems and the attacked lines respectively. We test all the lines of both systems but only showing few of them in table chosen randomly. We make a comparison between a single topology attack (base case) and the proposed one. Single LF column represents a single line failure as a result of an undetectable attack whereas Sequential LF column shows the proposed attack where the attacker opens and closes the breaker sequentially during measurement taking process. The mean-square error (MSE) between two vectors is simply a squared Euclidean distance between them, normalized by the length of the vectors. It can be seen for the two transmission lines in 30-bus system, i.e., 2–4 and 24–25 that the system diverge due to singularities after removing these lines. Even for such critical lines (a transmission line between a pair of buses whose removal leave the system disconnected), the proposed attack (Sequential LF) outperforms the single LF by forcing the state estimator and not just breaking down the system. It is mainly due to the fact that the proposed method can avoid detection because the topology state of the system remains the same before and after the measurement process. Table 1 illustrates that the proposed model works better than the basic one in almost every respect and shows even better results for the larger grid.

6 Conclusion

The frequent topology changes make our grid more vulnerable to topology attacks where the operator can think of the attack as the usual unplanned change. We propose a transient topology attack involving sequential failures during a single scan cycle. This way, the state of the topology remains same in the beginning and the end of the process of collecting measurements therefore, making the attack adequately undetectable. Finally, an optimization problem for the least cost attack is formulated.

Results show adequate success of the model and our ongoing work includes understanding the behaviour and criticality of these faults in different topologies and different systems. We will possibly be looking at if same might be true for PMU measurements as they often consider as equality constraints and don’t have to go through bad data detection.